基于主成份的多重分形法在岩性识别中的应用*

张 焱, 周永章,朱继田

(1. 中海石油(中国)有限公司湛江分公司，广东 湛江 524057;2. 中山大学地球科学与地质工程学院，广东 广州 510275)



基于主成份的多重分形法在岩性识别中的应用*

张 焱1, 周永章2,朱继田1

(1. 中海石油(中国)有限公司湛江分公司，广东 湛江 524057;2. 中山大学地球科学与地质工程学院，广东 广州 510275)

为解决测井曲线识别复杂油气藏岩性存在的多解性和不确定性问题，利用测井曲线信息构建主成份变量，采取累积方差大于85%的主成份作为输入信息代表，既保证输入变量最少又保证损失信息最小，通过简化数据结构来识别岩性。根据琼东南盆地深水区某区储层实测的自然伽马(GR)、深电阻率(RES_BD)、中电阻率(RES_BM)、浅电阻率(RES_BS)、中子孔隙度(TNPH)、体积密度(RHOB)、声波时差(DTCO)值，构建7个综合变量，其中主成份1和主成份2两个主变量占总贡献率的85.11%，可以有效地代替该区储层实测的7个变量所包含的综合信息。研究表明，通过井壁心定名的岩性数据，根据主成份1和主成份2的交会图分析，可以有效地识别该区域的粉砂岩、泥岩、细砂岩。为进一步说明岩性识别的确定性，文中采用多重分形法对测井曲线进行研究，分析了谱函数曲线，结果表明，砂岩段对应的谱函数曲线右偏，泥岩段对应的谱函数曲线左偏，这一结论可以作为砂岩泥岩区分的有效证据。

琼东南盆地; 深水区；岩性识别；主成份；多重分形；谱函数

油气藏实际工作中，岩性识别是储层评价的重要工作之一，也是求解储层参数的基础[1]。如何更准确的揭示岩性对测井的影响从而提高岩性解释的准确度，成为勘探中急需解释的问题[1]。而根据测井信息可以得知储层岩性[2]。由此可见测井信息在岩性识别中占有相当的重要地位[3]。尤其当岩性复杂多变时，由于其储层的非均质性而导致的岩性识别困难等问题已经成为人们研究的热点问题[4]，最传统的方法是采用岩性交会图方法来识别复杂岩性[5-7]。这种传统的岩性交会图一般只应用两种直接的测井变量，而忽略了更多与岩性相关的变量，而且一旦这两个变量存在着明显的相关性，问题就显而易见了，导致的直接后果就是交会图的精度降低[8]。而采用降维思想的主成份分析法可以在既保证信息损失最小又能保证输入量最少的情况下进行岩性识别，可以有效地解决传统交会图分析中存在的问题。

近年来多重分形法由于能够提供比单一分形更多的信息而倍受关注[9-10]，多重分形分析可以计算出包括单一分形分维数在内的多重分形谱[11-12]，在对测井信息进行分析时，可以提供比单一分形更多的信息。而根据谱函数曲线的特征可以有效的识别岩性，这无疑又为岩性识别工作开辟了另一条光明途径。文中首次将谱函数用于岩性识别，并用于琼东南盆地深水区，该方法可以作为主成份交会图岩性识别的有效补充。

1 研究区简况

琼东南盆地是我国南海北部深水区油气勘探的重要领域之一[13-14]。该盆地深水区最大水深超过3 200 m[15]。琼东南盆地深水区某区域岩性主要为粉砂质泥岩、泥质粉砂岩、粉砂岩、泥岩，细砂岩次之。粉砂岩含量大约为：6%；粉砂质泥岩含量大约为2%，泥岩含量大约为74%，泥质粉砂岩含量大约为18%(图1)。

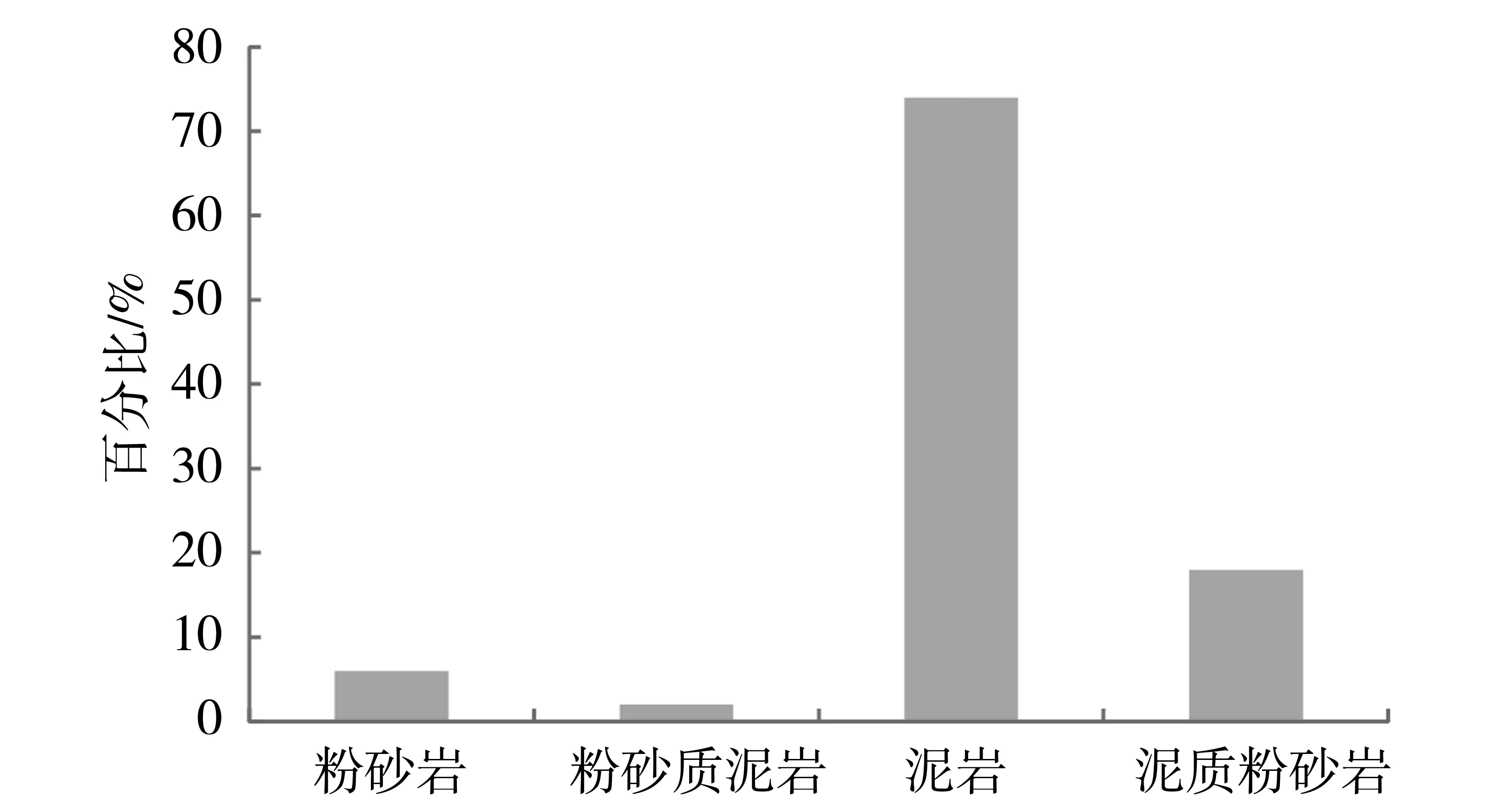
图1 琼东南盆地深水区某区岩性分布图Fig.1 Lithologic map for deep-water section in Qiong basin

2 主成份分析法在岩性识别中的应用

2.1 主成份分析法原理

主成份分析是对数据降维的一种方法，其基本思想是将原来众多的具有一定相关性指标X1,X2,…,XP(如有P个指标)，重新组合成一组较少个数的互不相关的综合指标Fm来代替原指标[16]。综合指标要求既能最大程度的反映原变量Xp所代表的信息，又能保证新指标之间的相互无关(信息不重叠)[12]。

其计算步骤为[16-17]：

1)原始指标数据的标准化采集p维随机向量x= (X1,X2,...,Xp)T)n个样品xi= (xi1,xi2,...,xip)T，i=1,2,…,n，n>p，构造样本阵，对样本阵元进行如下标准化变换：

(1)

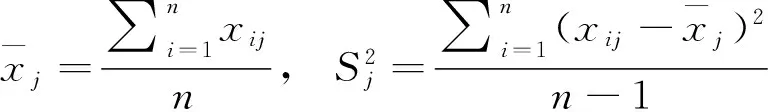
2)对标准化阵Z求相关系数矩阵。

(2)

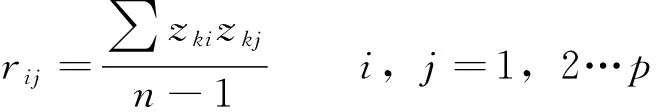
3)解样本相关矩阵R 的特征方程|R-λIp|=0得p个特征根,确定主成分。

4)将标准化后的指标变量转换为主成分。

(3)

U1称为第一主成分,U2称为第二主成分,…,Up称为第p主成分。

5 )对m个主成分进行综合评价。

对m个主成分进行加权求和，即得最终评价值，权数为每个主成分的方差贡献率。

2.2 应用实例

利用岩石样本的自然伽马(GR)、深电阻率(RES_BD)、中电阻率(RES_BM)、浅电阻率(RES_BS)、中子孔隙度(TNPH)、体积密度(RHOB)、声波时差(DTCO)值作为输入参数X=[ GR, RES_BD, RES_BM, RES_BS, TNPH, RHOB, DTCO]，以实验室45颗岩心分析岩性作为岩性判别依据(表1)，对其进行主成份分析，得到相关系数矩阵和对应的特征值、方差贡献率。

通常在进行主成份分析之前需要对样本数据进行标准化处理，使每个变量的均值为0，方差为1(表2)，以消除各参数量纲和数量级不同而导致的系统误差。标准化之后各样本数据量纲和数量级在同一个范围之内(图2)。根据标准化数据计算得到的相关系数矩阵见表3，由相关系数矩阵得到其特征值和方差贡献率(表4)。

由上述计算得知，主成份1方差贡献率最大，达到69.722%，主成份2次之，达到15.388%，主成份1和主成份2累积方差贡献率达到85.11%，这说明主成份1和主成份2这两个变量可以代替原来的7个变量，且保证数据信息损失小。根据上述主成份计算模型，对研究区45颗岩心样本进行主成份计算，由得到的最主要主成份1(PCA1)和次要主成份2(PCA2)对岩性进行交会图分析。常规的自然伽马和声波时差交会图(图3)上，很难区分砂岩类和泥岩类，而主成份交会图(图4)可以有效的区分砂岩类、泥岩类储层，以至于细分出粉砂岩类储层。根据研究区内某井实际资料得知，其岩性识别具有较高的符合程度。

表1 研究区内岩性测井响应参数值

表2 样本数据标准化值

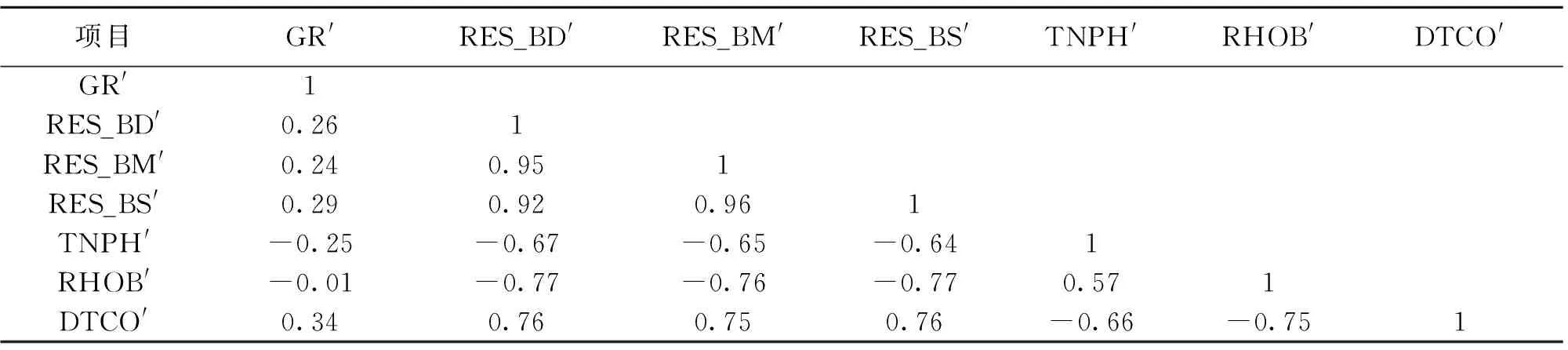
表3 相关系数矩阵

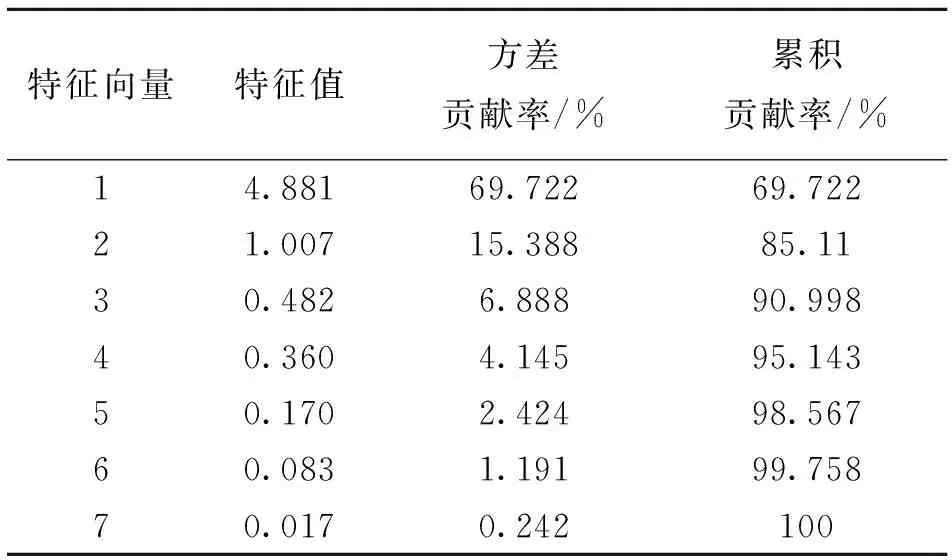
表4 特征值对应的单位化特征值、方差贡献率

图2 原始样本数据与标准化样本数据分布范围Fig.2 Distribution of the original and standardized data of samples

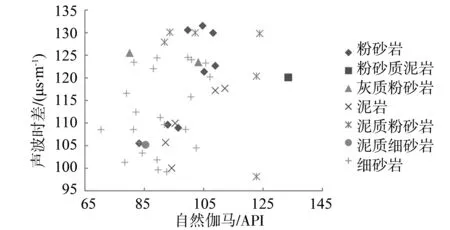
图3 自然伽马与声波时差交会识别岩性Fig.3 Lithology identification through GR-AC crossplotting

图4 主成份交会识别岩性Fig.4 Lithology identification through PCA crossplotting

3 测井曲线的多重分形方法研究

3.1 多重分形谱原理描述

设分形集F的奇异性指数为α，与α对应的Hausdorff维数为f(α)，用尺度为δ的单元覆盖分形集F，需要的单元数记为n，那么分形集F上概率测度分布P的q阶矩X(q，δ)定义为[11,18]

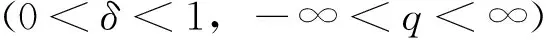
(4)

通常情况q取整数。按Hausdorff测度的定义，X(q，δ)的s维测度Hs(q)为

(5)

(6)

Hs(q)随着s的变化满足：

(7)

其中τ(q)为质量指数。

(8)

根据法尔科内[19]，奇异性指数和分形维数及质量指数之间存在如下关系

(9)

(10)

那么根据上述方程可以求出奇异指数α分形维数f(α)，从而得到多重分形谱。

综合上述公式得知

(11)

(12)

3.2 应用实例

采用多重分形谱算法对研究区内45颗岩心样本数据进行处理，由前面采用主成份分析结果得知，样本可以分为粉砂岩类、泥岩类、细砂岩类3大类，此处对这3类样本进行多重分形谱分析，为了说明粉砂岩类、细砂岩类、泥岩类分形谱维数形态的不同，分别选取3段数据进行维数谱分析，为避免数据交叉影响分析效果，前提条件是保证3段数据深度域不重合，选取的几个深度范围分别为：① 3 207～3 211.5 m；② 3 212.8～3 401.5 m；③ 3 405～3 417 m。计算这几个深度域的多重分形谱时，此处选用声波时差DTCO作为说明(选用其他参数结果相同)。对3个深度域测井曲线计算其多重分形谱(表5)，从表5可知，随着q值不断增大，a值逐渐减小，相应的f(a)值呈先增大后减小的趋势，图5是根据表5中a-f(a)关系值所得的结果图。

前人采用参数法分析分形谱函数曲线[20-21]，其中α0为q=0时α的值,

(13)

(14)

(15)

R=0时表示谱函数曲线两侧完全对称,R>0表示谱函数曲线向左偏,R<0表示谱函数曲线向右偏。表6列出了各深度域谱函数的ΔαL、ΔαR和R值。由分析结果得知，粉砂岩段和细砂岩段R值都为负值，这表示粉砂岩和细砂岩段对应的谱函数曲线向右偏，而泥岩段R值为正值，这说明泥岩段对应的谱函数曲线向左偏(图4)。由此可以得出结论：砂岩段对应的谱函数曲线右偏，泥岩段对应的谱函数曲线左偏。这一结论可以作为砂岩泥岩区分的有效证据。

进一步结合声波曲线图(图6)，从曲线图中可以看出深度区间3 400～3 412、3 208～3 212、3 221～3 224.5 m等段曲线变化明显，也是地层非均质性较强的区间段。以3 400～3 412 m、3 208～3 212 m为例，这两段曲线-qmax对应的α值最小，而从最高点到的-qmax对应f(a)形态一致，这说明这两段区间内地层的非均质性相同，而对于非均质性较好的地层，与-qmax对应的位置较低[11]，也即f(a)值较小，这也是符合实际要求的。由此可见，声波曲线多重分形谱的这些特征对于研究地层的非均质性也是很有意义的。

图5 不同井段多重分形谱计算示例Table 5 Multi-fractal spectrum of different sections of the well sample calculation

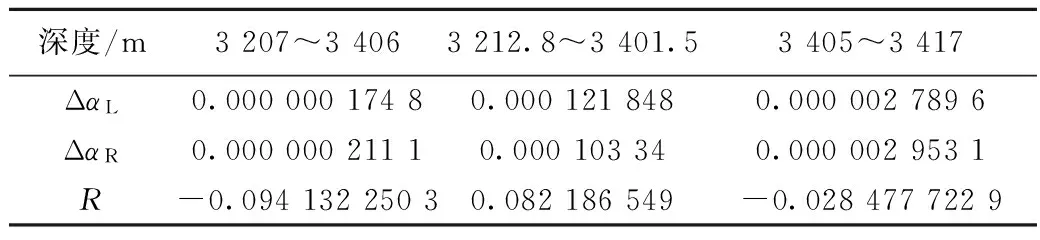
深度/m3207～34063212.8～3401.53405～3417ΔαL0.00000017480.0001218480.0000027896ΔαR0.00000021110.000103340.0000029531R-0.09413225030.082186549-0.0284777229

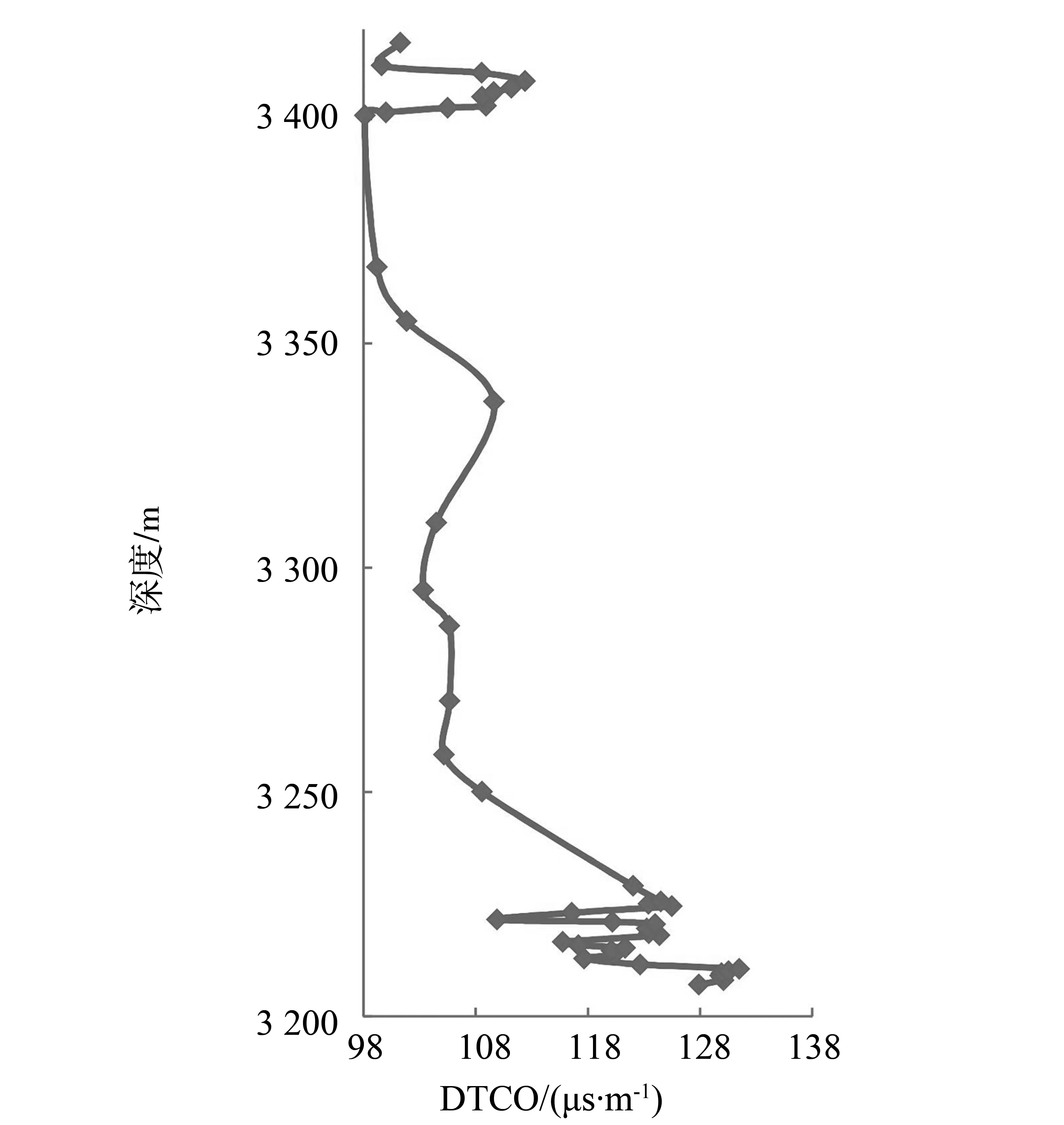
图6 声波曲线图Fig.6 AC curve

4 结 论

识别岩性复杂区域的关键是综合利用各种对岩性敏感的信息，如测井信息，文中采用主成份交会图法与常规测井交会图法进行对比，结果表明，主成份交会图法由于综合了多种测井信息能突出岩性特征的主成份变量，最大程度的保留了主要信息，减少了有效信息的损失。采用累积方差贡献率大于85%的主成份变量做交会图，可以有效的区分粉砂岩、泥岩、细砂岩储层，克服了采用传统测井交会图识别岩性的困难，在琼东南盆地深水区取得了较好的效果。

多重分形可以提供比单一分形更丰富的信息，测井曲线的多重分形谱特征对于研究地层非均质性是很有意义的，非均质性相同，多重分形谱特征相近，反之则不同。根据函数谱特征的偏移情况可以有效的区分砂岩类和泥岩类，谱特征可以作为区分砂岩泥岩的有效证据。总之，分形谱的非线性动力学特征为实际生产中的岩性识别起到了锦上添花的效果。

[1] 张涛, 莫修文. 基于交会图与模糊聚类算法的复杂岩性识别[J]. 吉林大学学报：地球科学版, 2007,37(增刊): 109-113.

[2] 赵军, 王淼, 闫爽, 等．自然电位测井在低阻油气层识别中的应用-以塔里木盆地吉拉克地区三叠系低阻油气层为例[J]．石油与天然气地质, 2011, 32( 2) : 245-250．

[3] 赵军, 肖承文, 虞兵, 等. 轮古地区碳酸盐岩洞穴型储层充填程度的测井评价[J]. 石油学报, 2011, 32(4): 605-610.

[4] 李易隆, 贾爱林, 何东博. 致密砂岩有效储层形成的控制因素[J]. 石油学报, 2013, 34(1): 71-82.

[5] 李旭兵, 刘安, 曾雄伟, 等. 雪峰山西侧地区寒武系娄山关组碳酸盐岩储层特征研究[J].石油实验地质, 2012, 34( 2) : 153-157．

[6] 罗小龙, 汤良杰, 谢大庆, 等. 塔里木盆地雅克拉断凸中生界底界不整合及其油气勘探意义[J].石油与天然气地质, 2012, 33( 1) :30- 36．

[7] 雍世和，张超谟． 测井资料处理与解释[M]． 山东东营: 石油大学出版社，2004: 80-96．

[8] 刘爱疆, 左烈, 李景景, 等. 主成份分析法在碳酸盐岩岩性识别中的应用[J]. 石油与天然气地质, 2013, 34(2): 192-196.

[9] 张焱, 周永章, 黄锐, 等. 粤北刘家山地区多元素分形维数谱函数及其对矿化的指示分析 [J]. 中山大学学报：自然科学版, 2012, 51(2): 119-124.

[10] ZHANG Yan, ZHOU Yongzhang, WANG Linfeng, et al. Mineralization-related geochemical anomalies derived from stream sediment geochemical data and their decomposition using multifractal analysis in the Pangxidong area of Qinzhou-Hangzhou tectonic joint belt, Guangdong Province (China)[J]. Journal of Central South University, 2013, 20(1): 184-192.

[11] 文环明, 肖慈, 李瑞, 等. 测井曲线的多重分形分析方法研究[J]. 测井技术, 2004, 28(5): 381-385.

[12] 张焱, 周永章, 姚凌青, 等. 多重分形与地质统计学方法在粤北刘家山地区矿化指示中的应用[J]. 地学前缘, 2012, 19(4): 151-158.

[13] 吴时国, 袁圣强. 世界深水油气勘探进展与我国南海深水油气前景[J] . 天然气地球科学, 2005, 16(6) : 693-699.

[14] 雷超，任建业，李绪深, 等. 琼东南盆地深水区结构构造特征与油气勘探潜力[J].石油勘探与开发, 2011, 38(5): 560-569.

[15] 王振峰, 李绪深, 孙志鹏, 等. 琼东南盆地深水区油气成藏条件和勘探潜力[J]. 中国海上油气, 2011,23(1): 7-13.

[16] 朱星宇，陈勇强. SPSS多元统计分析方法及应用[M].北京：清华大学出版社，2011：241.

[17] 向东进, 李宏伟, 刘小雅. 实用多元统计分析[M ] . 武汉: 中国地质大学出版社, 2005.

[18] 辛厚文. 分形介质反应动力学[M]. 上海: 上海科技教育出版社, 1997.

[19] (英)KENNETH J FALCONER. 分形几何——数学基础及其应用[M]. 曾文曲, 刘世耀, 戴连贵, 等译. 沈阳: 东北大学出版社, 1991.

[20] GALUSZKA A. A review of geochemical background concepts and an example using data from Poland[J]. Environmental Geology, 2007,52(5):861-870.

[21] XIE S, CHENG Q, CHEN G, et al. Application of local singularity in prospecting potential oil/gas targets[J]. Nonlinear Processes Geophysics, 2007, 14: 285-292.

Multi-Fractal Method’s Application Based on Principal Component in Lithology Recognition

ZHANGYan1,ZHOUYongzhang2,ZHUJitian1

(1. China National Offshore Oil Corporation Limited, Zhanjiang 524057, China;2. School of Earth Science and Geological Engineering, Sun Yat-sen University,Guangzhou 510275, China)

In order to solve the problem that logging curve identifying complex reservoir lithology has multiplicity and uncertainty, this paper uses logs to build principal component variables and takes the principal components with the cumulative variance greater than 85% as input information, ensuring that input variables are minimum and information loss is minimal. and then simplifies the data structure to identify lithology. Based on measured values of gamma ray (GR), deep resistivity (RES_BD), resistivity (RES_BM), shallow resistivity (RES_BS), neutron porosity (TNPH), bulk density (RHOB) and interval transit time (DTCO) in deep-water reservoir of the Qiongdongnan Basin, seven integrated variables were constructed. Principal component 1 and principal component 2, with the total explained variance of 85.11%, can effectively explain the comprehensive information of seven variables. Based on lithologic data obtained from side-wall core, siltstone, mudstone,and fine sandstone can be identified on the cross plot of principal component 1 and principal component 2. Additionally, the multi-fractal method was used to analyze the spectral function curves. The sandstone corresponds to spectral function curve leaning right and mudstone corresponds to spectral function curves leaning left, which can be used as valid evidence to distinguish sandstone and mudstone.

southeast Qiong basin; deep-water area; lithology identification; principal component; multifractal; spectral function

10.13471/j.cnki.acta.snus.2015.03.025

2014-10-10

“十二五”国家重大科技专项基金资助项目(2011ZX05025)

张焱(1983年生)，女；研究方向：石油地质与数学地质；E-mail:zhang_yan1117@163.com

P628

A

0529-6579(2015)03-0145-07