基于车致振动响应的含分布损伤桥梁结构识别方法*

李海龙，吕中荣，刘济科

(中山大学应用力学与工程系，广东 广州510275)



基于车致振动响应的含分布损伤桥梁结构识别方法*

李海龙，吕中荣，刘济科

(中山大学应用力学与工程系，广东 广州510275)

采用Newmark直接积分法和龙格库塔法求解了非线性车桥耦合系统的振动响应 ，并利用加速度响应灵敏度方法对含裂纹梁结构进行分布类型的损伤识别。文中车辆采用含非线性弹簧的半车模型，桥梁被离散为欧拉梁单元，裂纹引起的桥梁损伤模拟为桥梁局部刚度的线性分布的减少。数值算例表明，在5%噪声情况下，加速度响应灵敏度方法依然可以较准确地识别出桥梁损伤的分布情况。

车桥耦合系统；动力响应；非线性弹簧；裂纹识别；灵敏度

在过去几十年中，随着经济和科技水平的发展，世界各地修建了越来越多的大跨度桥梁。这些桥梁在使用过程中由于材料老化、疲劳和其他不利因素的影响下很容易产生损伤裂纹，进而影响桥梁结构的耐久性和行车舒适性，甚至引发灾难性事故。因此，对桥梁结构的损伤裂纹进行识别和监测研究具有重要的理论和现实意义。

已有许多种损伤识别方法被提出来并在工程中得到初步应用[1-2]，主要分为频域、时频域、和时域。早期发展的主要是频域方法[3],根据固有频率、振型、柔度曲率、模态能量等数据识别结构损伤[4-8]。但是，频域法易丢失原始数据的部分损伤信息，损伤识别结果往往不够准确。

随着计算机和数学的发展，损伤识别方法发展了时频域方法[9-10]，利用信号分析工具对结构的响应进行分析，获得结构的时频特性，从而对结构进行损伤识别。近年来，直接利用结构振动响应进行损伤识别的时域[11-12]方法逐渐受到学者的重视。Lu和Law[13]提出的基于响应灵敏度的时域方法既能准确识别出结构的损伤参数，并且所需测点数量较少，具有一定的工程应用潜力[14-16]。

本文采用Newmark直接积分法和龙格库塔法求解了非线性车桥耦合系统的振动响应 ，并利用加速度响应灵敏度方法对含分布裂纹梁进行结构损伤识别。文中车辆采用含非线性弹簧的半车模型，桥梁被离散为含有线性分布裂纹的二维欧拉梁单元。数值算例表明，在5%噪声情况下，加速度响应灵敏度方法依然可以准确的识别出桥梁损伤的位置及程度。此外，当裂纹区域增大后，需要更多的加速度计测点才能获得较为准确的识别结果。

1 车桥耦合系统的动力响应

1.1 车辆振动方程

根据达朗贝尔原理，车辆的振动方程可以表示为

(1)

其中Fs1、Fs2、Ft1和Ft2是车辆四个弹簧的附加弹性作用力，车辆的其他参数如图1所示。

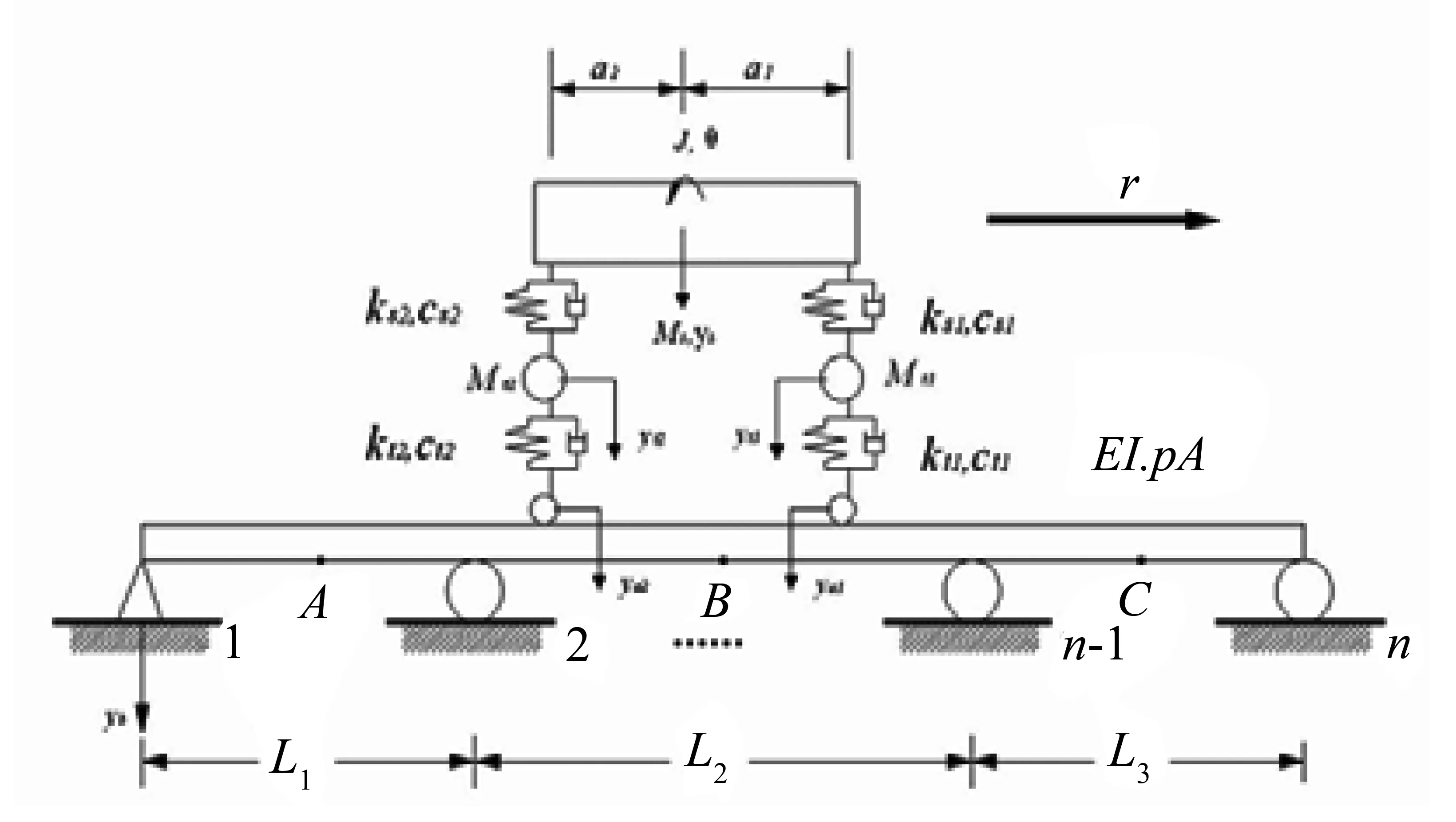
图1 车桥耦合系统示意图Fig.1 Vehicle-bridge system

1.2 桥梁振动方程

离散化后的桥梁强迫振动方程可表达为

(2)

其中{yb}为竖向位移向量，{Fb}为节点力向量 ，

[Mb]、[Cb]和[Kb]分别为桥梁系统质量矩阵、阻尼矩阵和刚度矩阵。本文中采用瑞利阻尼矩阵，即[Cb]=α1[Mb]+α2[Kb]，其中α1和α2为常数。

1.3 车桥耦合系统间的相互作用力

本文中，车桥耦合系统被分为两个动力子系统——桥梁振动子系统和车辆振动子系统，并且假设二者之间始终紧密接触。车辆和桥梁间的相互作用力可以表达为

(3)

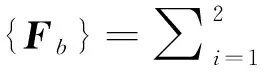
本文采用Newmark直接积分法和龙格库塔法求解车桥耦合系统的动力响应。

1.4 车辆非线性弹簧

通常情况下，车体与车轮之间的弹簧被简化为线性的。但是在复杂的路面条件和荷载情况下，线性弹簧的特性并不适用。为了提高行车舒适度，工程师们常常采用非线性弹簧来提高弹簧的特性。非线性弹簧可以表达为

F=kx+μkx3

(4)

此处μ为小参数，如果弹簧是线性的，则μ=0；如果弹簧是非线性的，μ>0。

所以，方程(1)中弹簧的附加作用力可以表达为

(5)

1.5 分布裂纹模型

本文采用材料的杨氏模量的减小来表达桥梁的损伤程度，并且假设在桥梁的裂纹区域内，杨氏模量是线性变化的，图2为梁上裂纹示意图。

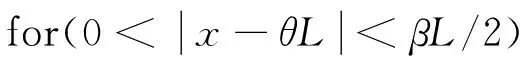
(6)

其中L为桥梁长度，x为梁上任一点到裂纹区域中点的距离，θL为裂纹区域中点的位置。η代表了裂纹的大小，而β代表了裂纹的长度。E0为无损伤梁的杨氏模量。

图2 裂纹模型示意图Fig.2 The distribution of the Young’s modulus along the beam

2 响应灵敏度损伤识别方法

(7)

与其他逆问题相似，灵敏度矩阵[S]是病态的，其中的微小奇异值会导致非满秩矩阵。直接使用最小二乘法求解也会产生无限多个解，所以本文采用Tikhonov[17]提出的阻尼最小二乘法(Damped Least-squares)求解{Δα}。

3 数值算例

桥梁长度L=50 m，密度ρ=2 500 kg/m3，抗弯刚度EI=1.275×1011Nm2。双轴车辆模型的参数如下

Ms=35 470 kg,Mt1=1 500 kg,

Mt2=1 000 kg,a1=2.22 m,a2=2.05 m,

ks1=2.47×106Nm-1,ks2=4.23×106Nm-1,

kt1=7.48×106Nm-1,kt2=9.20×106Nm-1,

cs1=3×104Nm-1s,cs2=4×104Nm-1s,

ct1=3.90×103Nm-1s,ct2=4.30×103Nm-1s,

J=1.47×105kgm2,μt1=0,μt2=0,

μs1=5×108,μs2=5×108

在计算车桥耦合系统响应过程中，桥梁被离散为20个欧拉梁单元，车辆速度为10 m/s，时间步长0.002，前两阶模态阻尼比为0.01。当桥梁只含有一个分布裂纹且裂纹参数为η=0.85，β=0.4，θ=0.5时，在桥梁的6号、8号、12号、13号、16号节点上分别放置一个加速度计。

图3和图4画出了在无噪声和5%噪声时的识别结果。从图中可以看出，在无噪声情况下，此方法可以非常精确的识别出单元刚度参数减少的分布，在5%噪声情况下，识别结果有一定误差，但是依然比较准确。这是因为在无噪声情况下，计算的响应可以与模拟测量响应非常接近，但是在5%噪声情况下，模拟测量响应数据被噪声污染，计算的响应不能与含噪声的模拟测量响应完全重合。

图3 单裂纹、无噪声时的识别结果Fig.3 The identified results of a crack without noise

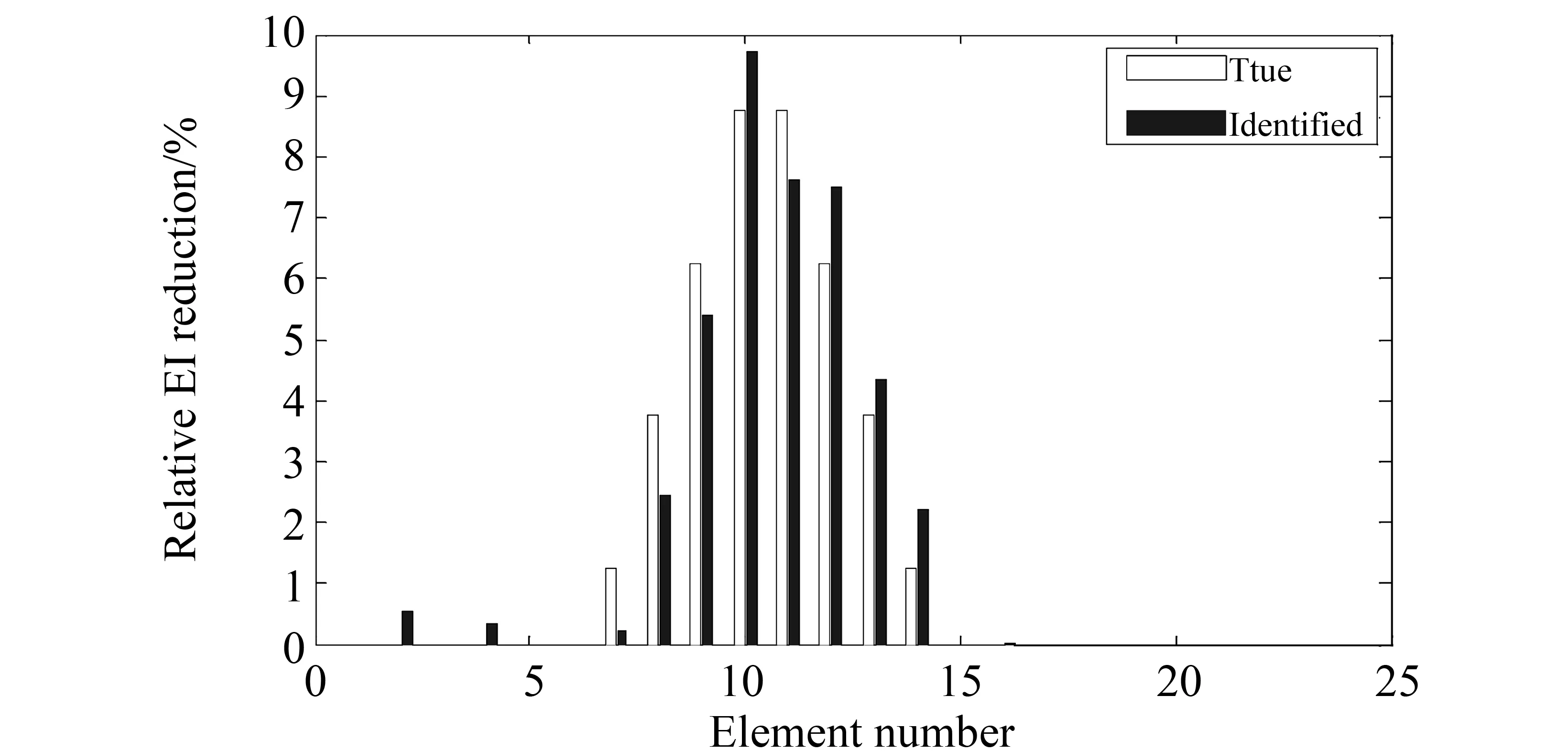
图4 单裂纹、5%噪声时的识别结果Fig.4 The identified results of a crack with 5% noise

桥梁含有两个分布裂纹，并且裂纹参数分别为η1=0.9，β1=0.3，θ1=0.5 和η2=0.95，β2=0.3，θ2=0.5。此时，由于裂纹区域增多，原有的5个加速度计测点结构无法准确的识别出裂纹参数，需要增加加速度计测点数量。在桥梁有限单元3、4、5、6、9、11、13、16、19号节点共布置9个加速度计时，识别结果比较理想。

图5和图6分别画出了在无噪声和5%噪声时的识别结果。结果表明，在无噪声情况下，加速度响应灵敏度方法可以十分精确地识别出桥梁单元刚度参数减少的分布。在5%噪声情况下，识别结果有一定误差，但是依然比较准确。

图5 双裂纹、无噪声时的识别结果Fig.5 The identified results of two cracks without noise

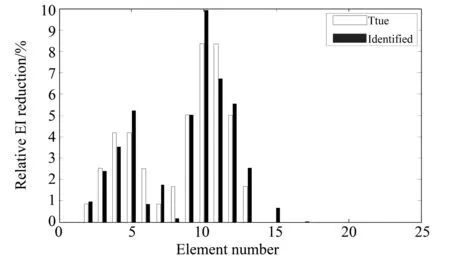
图6 双裂纹、5%噪声时的识别结果Fig.6 The identified results of two cracks with 5% noise

4 结 论

以上计算结果表明，当结构产生线性分布裂纹时，加速度响应灵敏度方法可以精确地识别出桥梁单元刚度参数减少的分布。此外，当裂纹区域增大后，需要更多的加速度计测点才能获得较为准确的识别结果。同时，本方法中车辆弹簧是非线性的，与实际情况更为接近，在试验验证和工程实际中有一定价值。

[1] SCOTT W D, CHARLES R F，MICHALE B P. A summary review of vibration-based damage identification methods [J]. Shock and Vibration Digest, 1998, 205: 631-645.

[2] 刘济科,汤凯. 基于振动特性的损伤识别方法的研究进展[J]. 中山大学学报:自然科学版, 2004,43( 6): 57-61.

[3] CARDEN E P, FANNING P. Vibration based condition monitoring: A review [J]. Structural Health Monitoring, 2004, 3(4): 355-377.

[4] CAWLEY P, ADAMS R D. The location of defects in structures from measurements of natural frequencies [J]. Journal of Strain Analysis, 1979, 14(2):49-57.

[5] PANDY A K, BISWAS M. Damage detection in structures using changes in flexibility [J]. Journal of Sound and Vibration, 1994, 169 (1): 3-17.

[6] LU Q, REN G, ZHAO Y. Multiple damage location with flexibility curvature and relative frequency change for beam structures[J]. Journal of Sound and Vibration, 2002, 253(5): 1101-1114.

[7] 杨秋伟,刘济科. 结构损伤识别的柔度灵敏度方法[J]. 中山大学学报:自然科学版, 2010, 49(1): 16-19.

[8] 唐小兵, 沈成武, 付军. 梁裂纹位置识别的模态能量法[J]. 武汉理工大学学报:交通科学与工程版, 2001, 25(3): 241-243.

[9] ZHU X Q, LAW S S. Wavelet based crack identification of bridge beam from operational deflection time history [J]. International Journal of Solids and Structures, 2006, 43 (7/8): 2299-2317.

[10] 任宜春, 易伟建. 基于小波分析的梁裂缝识别研究[J]. 计算力学学报, 2009, 22(4): 399-404.

[11] CHOI S, STUBBS N. Damage identification in structures using the time-domain response [J] Journal of Sound and Vibration, 2004, 275(3/4/5): 577-590.

[12] LU X B, LIU J K, LU Z R, A two-step approach for crack identification in beam[J]. Journal of Sound and Vibration, 2013, 332(2): 282-293.

[13] LU Z R, LAW S S. Features of dynamic response sensitivity and its application in damage detection [J]. Journal of Sound and Vibration, 2007, 303(1/2): 305-329.

[14] 吕中荣,王文洁,徐伟华,等. 基于振动响应的耦合杆系统损伤识别[J]. 中山大学学报:自然科学版, 2012, 51(5): 31-35.

[15] 安宁, 夏禾, 战家旺. 基于参数不确定列车作用下桥梁振动响应的桥梁损伤识别研究[J]. 工程力学, 2012 (10):275-281.

[16] 吕中荣, 徐伟华, 刘济科. 基于振动响应的耦合弦系统损伤检测[J]. 应用力学学报, 2009, 26(4):657-661.

[17] TIKHONOV A M. On the solution of Ill-posed problems and the method of regularization [J]. Soviet Mathematics, 1963, 4:1035-1038.

Identification of Distributed Damage in Bridges from Vehicle Induced Dynamic Responses

LIHailong,LUZhongrong，LIUJike

(Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275,China)

A distributed damage identification approach under moving vehicle loads is presented based on dynamic response sensitivity. Numerical studies are carried out on a simply supported beam under a vehicle with nonlinear springs for identication of distributed damage due to the crack. Combined Newmark direct integration method and Runge-kutta method are used to calculate the dynamic responses of the coupled bridge-vehicle system. The numerical results show that the distributed damage(s) can be identified accurately even with 5% noise in the measured acceleration data. And more accelerometers are needed if there are multiple cracks in the bridge.

bridge-vehicle system; dynamic response; nonlinear springs; damage detection; sensitivity.

10.13471/j.cnki.acta.snus.2015.03.002

2014-10-27

国家自然科学基金资助项目(11172333, 11272361)

李海龙(1989年生)，男；研究方向：结构损伤识别；通讯作者：吕中荣;E-mail:lvzhr@mail.sysu.edu.cn

O39

A

0529-6579(2015)03-0010-04