不同芯材增强材料抗压性能比较的有限元计算

宋孝浜， 王春霞， 金利民

(1. 盐城工学院 纺织服装学院， 江苏 盐城 224003； 2. 中国科学院 上海应用物理研究所，上海 201204； 3. 东华大学 纺织学院， 上海 201620)



不同芯材增强材料抗压性能比较的有限元计算

宋孝浜1， 王春霞1， 金利民2，3

(1. 盐城工学院 纺织服装学院， 江苏 盐城 224003； 2. 中国科学院 上海应用物理研究所，上海 201204； 3. 东华大学 纺织学院， 上海 201620)

为了分析不同芯材对 “O”形芯材增强复合材料抗压能力的影响，通过有限元计算，比较树脂、玻璃纤维、铁质3种芯材增强复合材料在相同压力作用下的力学行为。通过对比与分析材料挠度随时间的变化曲线、质量大小、应力分布及受力均衡性等指标发现：应力分布的对称性与承力均衡性对材料抵抗外力有利，即使其能够吸收较多的能量并产生较小的变形。此外，综合考虑抗压能力、承力均衡性以及轻质化等方面的要求，不应选用树脂或铁质芯材增强复合材料，而应选用玻璃纤维芯材增强复合材料。

芯材； 复合材料； 抗压； 有限元

近年来，随着高性能纤维材料与材料制备技术的飞速发展，纺织结构复合材料已经受到科研人员的日益重视并得到广泛应用，俨然已成为新型材料领域的研究热点之一[1]。在此类复合材料诸多优异的性能指标中，轻质高强是其最为显著的优势。一直以来，各种类型的纺织结构复合材料因卓越的轻质高强性能展示出了巨大的应用潜力，已在国民生产、生活的许多领域(如车辆、船舶、体育器材等[2-3])成为常规金属材料的优良替代品。而如何设计、制备出质量更轻、强度更大的纺织结构复合材料，更是材料领域广大科技人员的目标。

纺织结构复合材料的轻质化和高强度受到各组成相的制约，主要影响因素包括：增强相与基体相原材料的选择及搭配、增强相结构、各组分含量等[4-5]。理清并解决好以上问题后，通过科学合理的设计以争取在轻质化的同时，能够使材料达到更高的强度。目前已进行了探究复合材料轻质化与高强化方法的一系列工作[6-7]。增强相结构因素对复合材料的性能也具有一定的影响，如纤维取向角、预制体结构、芯材高度等[8-10]。现有研究成果给出了一些减轻材料质量、提高材料强度的方法。然而，鉴于某些情况下，对复合材料轻质化与高强化2方面的同时要求会导致设计上的矛盾。故应该在综合考虑2方面因素的基础上，寻求最合适的材料搭配与结构以制备最佳的材料。

本文运用有限元计算方法分析不同芯材对 “O”形中空复合材料抗压能力的影响。通过对比与分析材料挠度随时间的变化曲线、质量大小、应力分布及受力均衡性等指标阐述芯材的选择对复合材料抗压能力以及轻质化的影响，为轻质高抗压复合材料的设计提供有益的探索。

1 材料与模型

1.1 材 料

图1示出“O”形芯材增强复合材料的结构。由图可见，材料由处于内部的“O”形芯材增强体与包覆于外部的不饱和聚酯树脂基体构成，类似于皮芯结构型材料。即可认为以“O”形中空材料(本文中为不饱和聚酯树脂、玻璃纤维以及铁)为“芯”，以不饱和聚酯树脂为“皮”。其中，作为骨架材料的“O”形芯材一般是材料承载的核心部分，作为基体的树脂则具有固结增强相与传递载荷的作用。表1列出本文研究所用的各种材料的规格。

图1 “O”形芯材增强复合材料结构图Fig.1 Structure of O-shaped core reinforced composite

1.2 有限元模型

有限元模型如图2所示。利用有限元分析软件ABAQUS(版本：6.10)，32位版本Windows XP操作系统，根据材料结构及压力载荷的对称性特点，建立“O”形芯材增强复合材料的1/2细观结构有限元模型。对于网格设置，根据模型尺寸参数(图3)，确定网格格距。在短边、边角等处划分较多的网格，保证网格的合理精细度。此外，采用规则的C3D8R六面体单元，此类型的单元规整度好，计算的速度与精确度也较高。图3(a)示出模型的网格化效果，图3(b)示出载荷和边界条件，如材料上表面被施加100 MPa的压力，下端面的自由度被完全固定。

表1 材料规格

图2 有限元模型Fig.2 Finite element model.(a) Mesh scheme; (b) Loading and boundary conditions

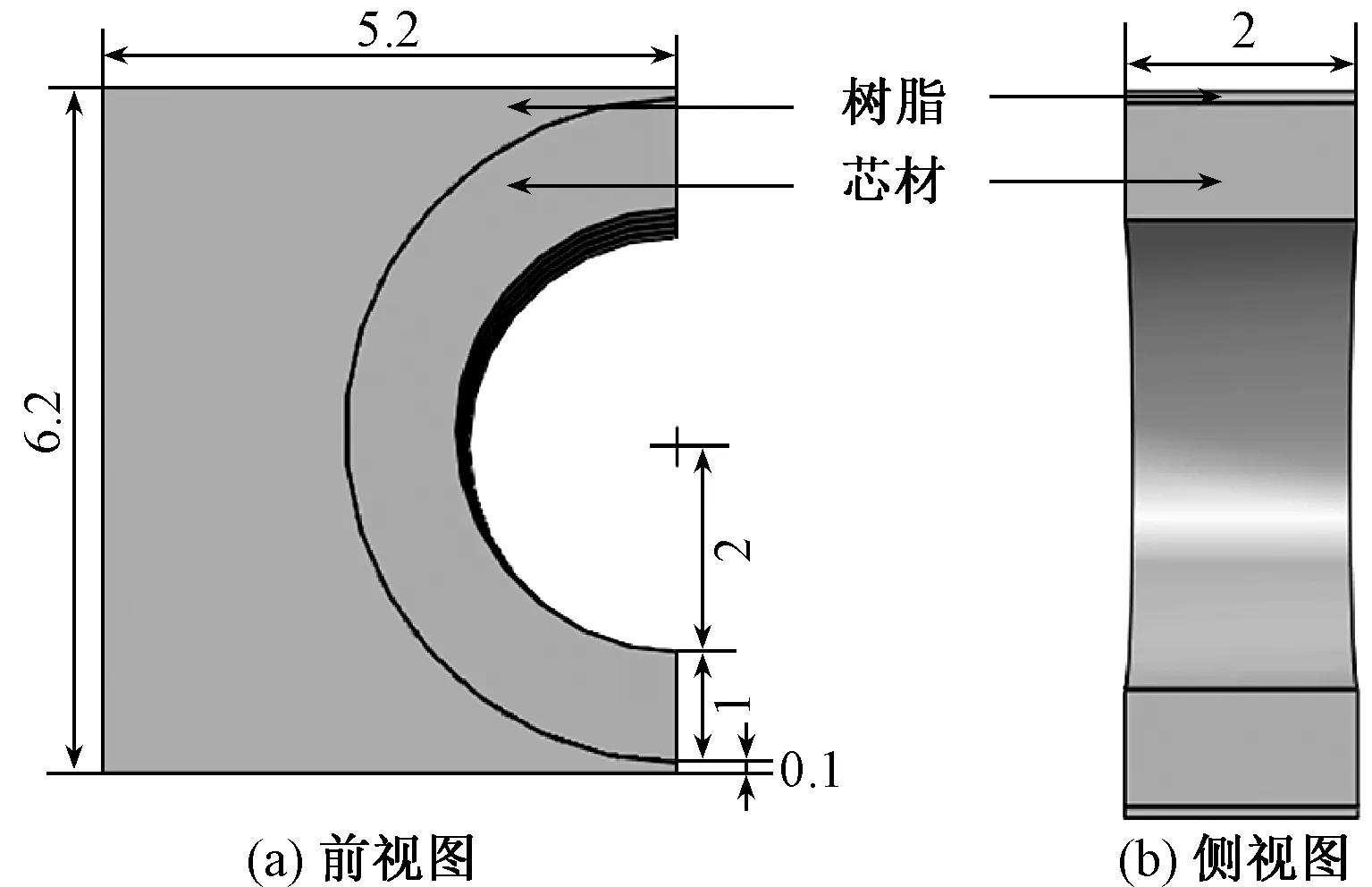
图3 复合材料1/2细观结构模型图Fig.3 1/2 micro-structural model of composite.(a) Front view; (b) Side view

2 结果与讨论

2.1 挠度-时间曲线

图4示出材料特殊点的挠度变化历程。为说明不同芯材对材料抗压性能的影响，如图4(a)所示，将每种材料以芯材为界分为a区、b区2部分，且分别在这2部分上取特殊点A、点B。图4(b)示出压力作用下3种不同芯材增强复合材料的A、B2点的挠度随时间的变化曲线。

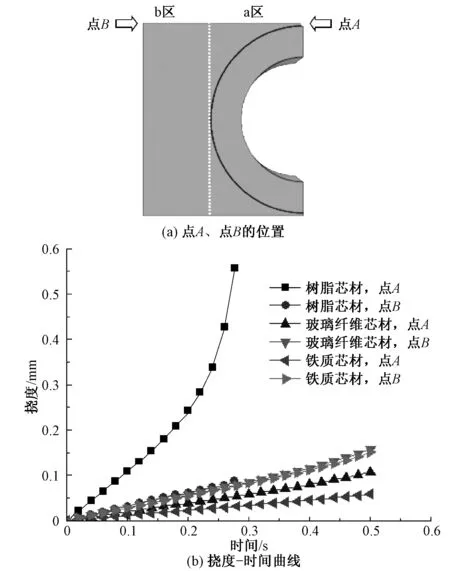
图4 材料特殊点的挠度变化历程Fig.4 Deflection history of specific nodes.(a) Locations of nodes A and B; (b) Deflection-time curves

从图4可看出，对于A点，按照挠度变化量的大小顺序，树脂芯材增强复合材料的挠度在短时间(0.27 s)内即发生大幅度的变化，达到0.56 mm；其次是玻璃纤维芯材增强复合材料，其挠度变化速率较树脂芯材增强复合材料小得多，总变化量(0.11 mm)也小；再次是铁质芯材增强复合材料，其挠度变化速率最为缓和，变化量(0.06 mm)也最小。同样地，对于B点，3种复合材料的挠度呈现出基本相似的变化速率与变化量。但与其他2种复合材料相比，铁质芯材增强复合材料的挠度变化最小。由此可见，3种材料中，铁质芯材增强复合材料的抗压性能为最佳。这是因为在其余条件(材料结构、边界条件、受力条件等)相同的情况下，不同芯材增强复合材料抗压能力的大小主要取决于芯材材质的选择。由于铁质芯材的力学性能优于玻璃纤维或树脂芯材，提高了材料整体的抗压强度，故挠度较小。

为说明芯材对复合材料抗压能力的贡献，将每种复合材料上A、B2点的挠度变化情况进行比较。从图4(b)可以发现：对于树脂芯材增强复合材料，其A点的挠度变化速率与变化量远高于B点，说明树脂芯材的存在不仅不能改善材料的抗压能力，反而会降低材料的抗压性能，即对材料抗压能力产生了“负”贡献，应该在实际应用中加以避免。而对于玻璃纤维芯材或铁质芯材增强复合材料而言，A点的挠度变化速率与变化量均比B点的小，即说明这2种芯材都可改善材料的抗压能力。但值得提出的是：相比于玻璃纤维芯材增强复合材料，随着施载时间的延长，铁质芯材增强复合材料A、B这2点的挠度变化差异将会越来越大，表现为材料受力表面的抗力不均匀性将越发显著，从而影响材料的抗压效果与持久性。

2.2 质量比较

根据表1示出的材料性能参数与结构尺寸，计算出每种芯材增强复合材料的质量，结果如表2所示。

表2 复合材料质量

从表2可发现，树脂芯材增强复合材料的质量最小，玻璃纤维芯材增强复合材料的质量较大，而铁质芯材增强复合材料的质量最大。进一步地，前二者的质量相差较小，约为35.8 mg，即在相同条件下，玻璃纤维芯材增强复合材料比树脂芯材增强复合材料约重35.8 mg。将这2种材料分别与铁质芯材增强复合材料相比，可发现非常显著的差异，即2种材料较之分别约轻202.22 mg与166.42 mg。因此，从高抗压能力与轻质化要求上考虑，不应该选用树脂芯材或铁质芯材增强复合材料，而应选用玻璃纤维芯材增强复合材料。

2.3 结构应力分布

为了阐述“O”形芯材增强复合材料吸能的机制，考察其在压力载荷下的应力分布情况，结果如图5所示。

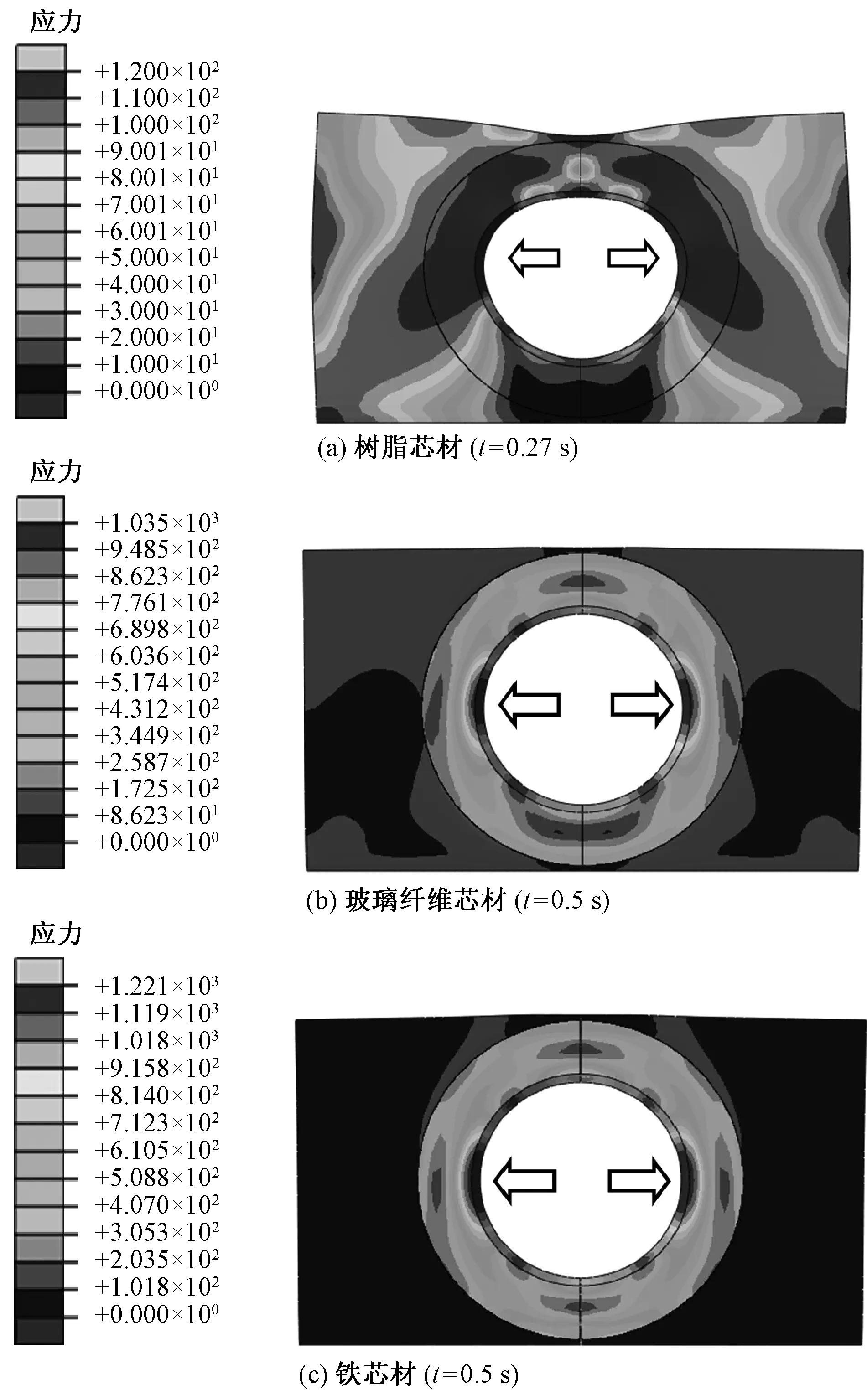
图5 复合材料结构应力分布Fig.5 Distribution of structural stress of composites.(a) Resin core (t=0.27 s); (b) Glass-fiber core (t=0.5 s); (c) Metal core (t=0.5 s)

从图5可看出：对于3种材料，结构应力集中部位都处于芯材的中间部位(图中箭头指示区域)。尤其是对于玻璃纤维芯材与铁质芯材增强复合材料，应力集中现象在结构上处于较为完美的对称状态，保证了材料上、下2部分的受力均衡性。这种对称性与均衡性对结构的整体承力有利，使其能够吸收较多的能量，从而导致较小的压缩变形。

从图5还可较为形象地考察复合材料受压面的变形情况。对于树脂芯材增强复合材料，其受压面呈现“边高中低”的倾斜状态，说明由于力学性能较弱的树脂芯材的存在，材料边端部分的抗压能力明显好于中间部分。这种承力不均衡性易导致施载过程中受力“失稳”现象的发生，对材料承力尤为不利。反之，再考察另外2种材料，由于性能较好的玻璃纤维或铁质芯材的存在，受压面无明显的倾斜态势(实际上呈现了轻微的“边低中高”)，很好地维持了承力均衡性，从而产生较小的变形。此现象与2.1小节所述内容一致。

3 结 论

1)对于压力作用下的不同“O”形芯材增强复合材料，树脂芯材增强复合材料的变形最大；其次是玻璃纤维芯材增强复合材料，其挠度较前者的小得多；而铁质芯材增强复合材料的变形最小。

2)树脂芯材的存在会降低材料的抗压性能，而玻璃纤维芯材或铁质芯材都可改善材料的抗压能力。此外，铁质芯材增强复合材料受力面的抗力不均匀性较为显著，影响抗压效果与持久性。

3)从高抗压能力与轻质化要求上考虑，不应选用树脂芯材或铁质芯材增强复合材料，而应选用玻璃纤维芯材增强复合材料。

4)对于玻璃纤维芯材与铁质芯材增强复合材料，应力集中现象在结构上处于较为完美的对称状态，保证了材料上、下2部分的受力均衡性。这种对称性与均衡性对结构的整体承力有利，使其能够吸收较多的能量，从而导致较小的压缩变形。

[1] MOURITZ AP, BANNISTER MK, FALZON PJ, et al. Review of applications for advanced three-dimensional fibre textile composites[J]. Composites Part A, 1999, 30: 1445-1461.

[2] 王宏雁, 周升波. 复合材料在汽车轻量化中的应用[J]. 汽车研究与开发, 2005 (9):20-23. WANG Hongyan, ZHOU Shengbo. Application of composites on light weight automobiles[J]. Automobile Research & Development, 2005 (9): 20-23.

[3] 张国腾, 陈蔚岗, 唐桂云. 复合材料轻量化技术在舰船制造领域的应用[J]. 纤维复合材料, 2010 (1):31-35. ZHANG Guoteng, CHEN Weigang, TANG Guiyun. Application of light weight composite technology in manufacturing ship[J]. Fiber Composites, 2010 (1): 31-35.

[4] 李福强, 陈福林, 岑兰, 等. 短纤维种类和用量对短纤维/EPDM复合材料物理性能的影响[J]. 橡胶工业, 2011, 58(3):163-166. LI Fuqiang, CHEN Fulin, CEN Lan, et al. The effects of categories and usage of short fibers on physical properties of short fiber/EPSM composite[J]. Rubber Industry, 2011, 58(3): 163-166.

[5] 姚力军, 耿林, 姚忠凯. 基体合金种类对SICw/AI复合材料拉伸性能的影响[J]. 材料科学与工艺, 1993, 1(1):23-27. YAO Lijun, GENG Lin, YAO Zhongkai. The influence of matrix alloy on the tensile property of SiCw/AL composite[J]. Material Science & Technology, 1993, 1(1):23-27.

[6] 何景轩, 何国强, 侯晓. 复合材料格栅圆柱结构优化设计[J]. 固体火箭技术, 2009, 32(1): 87-89. HE Jingxuan, HE Guoqiang, HOU Xiao. Optimization design of composite cylindrical lattice structure[J]. Journal of Solid Rocket Technology, 2009, 32(1): 87-89.

[7] 曲微微, 俞建勇, 刘丽芳, 等. 可降解黄麻/PBS复合材料的结构与力学性能[J]. 纺织学报, 2008, 29(8):52-55. QU Weiwei, YU Jianyong, LIU Lifang, et al. Structures and mechanical properties of biodegradable PBS composites reinforced by jute fiber[J]. Journal of Textile Research, 2008, 29(8):52-55.

[8] 丁辛. 复合材料梁结构的成型与弯曲特性[J]. 纺织学报, 1997, 18(6): 13-15. DING Xin. Formation of a composite beam and its flexural properties[J]. Journal of Textile Research, 1997, 18(6): 13-15.

[9] 郑蕊, 徐征, 李旭嘉, 等. 不同针刺预制体结构对C/C复合材料力学性能的影响[J]. 宇航材料工艺, 2012 (5): 26-29. ZHENG Rui, XU Zheng, LI Xujia, et al. Effect of needled preform structure on mechanical properties of C/C composite[J]. Aerospace Materials & Technology, 2012 (5): 26-29.

[10] 曹海建, 钱坤, 盛东晓, 等. 芯材高度对整体中空复合材料力学性能的影响[J]. 上海纺织科技, 2010, 38(9): 54-57. CAO Haijian, QIAN Kun, SHENG Dongxiao, et al. Influence of core height on the mechanical properties of 3D integrated hollow composites[J]. Shanghai Textile Science & Technology, 2010, 38(9): 54-57.

Finite element calculation for comparison of compression resistance of different core reinforced materials

SONG Xiaobang1， WANG Chunxia1， JIN Limin2,3

(1.CollegeofTextilesandClothes,YanchengInstituteofTechnology,Yancheng,Jiangsu224003,China;2.ShanghaiInstituteofAppliedPhysics,ChineseAcademyofSciences,Shanghai201204,China;3.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China)

In order to analyze the effect of different core materials on the compression resistance of the O-shaped core reinforced composites, the mechanical responses of three kinds of core materials of resin core and glass-fiber core as well as metal core reinforced composite under the same compression action were compared by the calculation using finite element analysis (FEA). By comparing and analyzing indexes of deflection-time curves, weight, stress distribution, and equilibrium degree of stress, it was found that both of the stress distribution symmetry and loading equilibrium were beneficial to the loading-bearing performance of the materials, even which can absorb more energy and generates relatively-small deformation. Furthermore, taking the requirements of compression resistance, loading equilibrium and light-weight into consideration, the glass-fiber core reinforced composite should be selected instead of resin or metal core reinforced composites.

core; composite; compression resistance; finite element

10.13475/j.fzxb.201501008805

2013-12-25

2014-04-25

宋孝浜(1969—)，男，教授，硕士。主要研究方向为纺织复合材料。金利民，通信作者，E-mail: lmjin@sinap.ac.cn。

TS 101.2

A