纤维与气流耦合的数值模拟

金玉珍， 李 俊， 林培锋， 吴震宇

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)



纤维与气流耦合的数值模拟

金玉珍， 李 俊， 林培锋， 吴震宇

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

结合纤维的本构方程与气流控制方程，建立二维的纤维与气流耦合方程。采用相容时间积分与迭代耦合算法，对纤维在喷气织机主喷嘴中拉伸弯曲运动特性、纤维受力情况以及与壁面接触时的微观运动特性进行研究。结果表明:纤维在气流的作用下会产生拉伸弯曲变形，呈现正弦或者余弦形式波动；纤维在自由端的弯曲变形效果比在约束端的明显；纤维受到气流作用时, 最大应力值往往发生在纤维弯曲部位以及与壁面相接触的部位。

流固耦合； 数值模拟； 纤维； 自适应网格

柔性体与流体耦合的数值模拟一直是流体动力型纺织机械基础研究领域的一大难题，国内外不少学者采用各种方法对纤维与气流两相耦合运动特点进行研究分析。Smith等[1]研究了纤维在二维加速层流中的运动状态。构造能够描述纤维惯性、空气拖曳力和弯曲刚度的非线性方程，数值模拟带有弯钩形状的纤维在气流的作用下被伸直。Kong等[2]构建了一个新的空气/纤维二维模型来模拟纤维在约束管道中的运动。通过模拟得到了沿着气流方向的纤维会产生弯曲，但是这个模型不能体现纤维的伸长、扭转等特性；Yamamoto等[3]提出了一种能够在流场中模拟刚性和柔性纤维运动的方法。纤维假设为N个相同半径的球相互连接而成，通过改变球与球之间的距离、调度、扭转角来获得纤维的拉伸、弯曲和扭转特性。通过求解流体动力和扭转力对单个球体的位移和旋转方程来获得纤维模型的运动。但在具体应用上，他们忽略了纤维的扭转，并且提出的珠链模型的计算成本很高。Lindstrom等[4]提出了一个柔性纤维在黏性流体中的运动模型，纤维被看成由纤维段连接而成，通过与气流的黏性与动态拖曳力来描述。Takemura等[5]采用浸没边界法模拟单根纤维在低雷诺数的剪切流的运动变化。数值模拟的结果显示了流体黏度的增加会使纤维运动变得更加复杂。Tornberg等[6]采用非局部细长体理论将流体对细丝的作用力与细丝的速度联系起来，以此建立纤维弯曲与拉力的数学模型。采用有限差分法模拟了单根柔性细丝以及相互作用的多根细丝在剪切流中的运动，结果显示流体剪应力会引起细丝的弯曲和松弛；Dong等[7]分别采用随机模拟和大涡模拟这2种方法模拟了柔性纤维在三维湍流中的运动变化，考虑了纤维与壁面之间的相互作用。结果显示纤维浓度在接近壁面附近呈线性变化，而其在远离壁面保持恒定。裴泽光等[8]采用N-S方程加ALE方程作为气流控制方程，并采用自适应网格的方法来改善网格畸变，研究纤维的运动变形。其研究结果能体现纤维柔性变形的特点，但对纤维的本构方程构建、纤维的变形特性未做详细的剖析。徐存强等[9]通过数值模拟与实验测试相结合的方法，反推出在不同相对速度下气流与纬纱的摩擦因素，得到了气流引纬主喷嘴内气流速度与纬纱间摩擦因素的关系。

已有国内外不少学者对柔性体与流体耦合的数值模拟做了很多探索性的工作，但迄今为止还没有形成公认可靠的、计算稳定的、快速的数值模拟方法。

针对纤维-气流耦合特性问题的研究，在原有Elastic-orthotropic材料模型基础上，结合纤维材料的特性修正了Elastic-orthotropic材料模型的本构方程以及相关参数，基于有限体积方法求解气流场，再对材料结构中的每个质点进行拉格朗日追踪，流体方程和材料本构方程按顺序相互迭代求解，直到两相耦合系统的解达到收敛，继而通过数据分析得到纤维材料在高速气流中的运动特性。本文研究为流体动力型纺织机械机制特性的进一步研究提供了一定的参考。

1 数学模型

1.1 纤维本构方程

纤维具有特殊的物理特征:长径比大，有弹性，当受到流场的作用力时会产生拉伸、弯曲等变形特性。假设纤维材料是线性弹性的，可以采用Elastic-orthotropic材料模型。二维模型中，纤维的本构方程[10]可以表示为

(1)

式中：σ11、σ22表示纤维在二维坐标轴上的2个主应力；相应的ε11、ε22为正应变；σ12代表纤维在二维坐标轴上的切向应力；相应的γ12为切向应变；kij为材料的刚度。材料的刚度可以通过材料的泊松比以及弹性模量等参数来调整。通过该本构方程就能够得到纤维应力与应变对应的函数关系。

1.2 纤维与气流控制方程

在二维直角坐标系下，不考虑密度变化以及热交换可以得到流体运动控制方程[11]：

(2)

(3)

(4)

式中：v和w分别是y轴和z轴上的速度；ρ和p分别是气流密度和压强。根据流体控制方程给出的变量，得出了流体模型的所需的入口条件以及初始条件，本文采用压力入口条件。

纤维的运动方程为

(5)

(6)

由于纤维被气流场包围，纤维与气流相互作用的部分发生在2个区域的交界面上，要满足以下2个条件。

运动学[12]条件为

(7)

动力学条件为

(8)

式中：df和ds分别表示纤维和气流在流固耦合面上的位移；σf和σs分别表示纤维和气流在流固交界面上的应力；n表示界面上的法向向量。

1.3 流固耦合相容时间积分

流体和结构模型中的时间积分必须是相容的。虽然流体模型采用的是Euler坐标系，结构模型采用的是Lagrange坐标系，但在流固耦合界面上都采用的Lagrange坐标系；因此，流体和结构模型中交界面上的位移、速度、加速度都是相同的。流体的速度和加速度[13]分别为

(9)

(10)

式中，α为时间复合积分系数。t+△t时刻的速度和加速度可以用位移未知量来表示。

(11)

(12)

式中，ξt、ηt分别为t时刻有关速度和位移的变化量。

将式(9)～(12)应用到耦合系统中。最终时间积分格式可以表示为

(13)

(14)

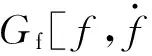
2 几何模型及边界条件设置

2.1 几何模型及相关参数

图1示出二维喷气织机主喷嘴与纤维的几何模型。模型中黑色的矩形代表了纤维所占据的区域，并将纤维的初始位置固定于喷嘴的中心轴线处，纤维的左端受到人为的约束作用，自由度为0；纤维的右端不受任何约束，自由度为y方向以及z方向的2个自由度。图1还示出喷嘴模型的压力入口、压力出口以及流固耦合壁面位置。气流场与纤维主要相关参数如表1、2所示。

图1 几何模型及其边界条件Fig.1 Geometric model and boundary conditions

入口条件/MPa出口条件/MPa单元大小/mm时间步长网格数量0.20.12×10-40.0011.1736×105

表2 纤维主要相关参数

2.2 纤维/壁面接触函数定义

纤维在高速气流中会产生大变形和自由运动，且在运动过程中有可能与壁面发生接触。纤维/壁面接触的动力方程[14]为

图2所示为纤维与壁面的接触，暂不考虑纤维与壁面之间的摩擦力。

设SXB为纤维与壁面接触的作用面，SBX为壁面与纤维接触的作用面，Sc=SXB∩SBX为t时刻纤维与壁面的接触面。定义接触函数为

(16)

将f表示交界面上的法向接触压力，则上述接触作用应满足的法向条件：

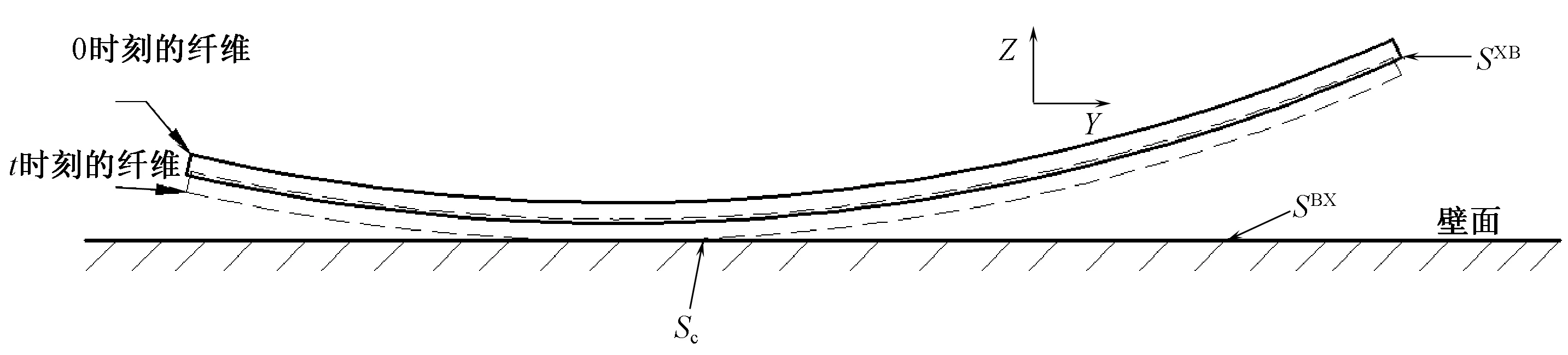
图2 纤维与壁面接触系统Fig.2 System of fiber and wall in contact

g≥0,f≥0,gf=0

(17)

如果g>0，则表示纤维与壁面没有接触，则f=0；如果g=0，则表示纤维与壁面之间存在接触，则f>0。

在模拟纤维与气流耦合的时候，由于接触函数的存在，当纤维接触壁面的时候，不会因为纤维与壁面的接触而停止计算。由于接触时f>0，壁面对纤维的作用力会使得纤维往反方向运动。

3 数值结果与分析

3.1 纤维的运动变形特性

对于纤维的弯曲变形特性，从宏观物理学上分析，即为纤维受到外力作用而产生体积或形状的改变；从微观定量上分析，即为纤维边界点偏离水平轴线的位移大小。研究中选取了6个时刻的纤维弯曲变形特点，如图3所示。

图3 纤维在6个时刻的弯曲变形情况Fig.3 Bending deformation of fiber at six moments

由图3可以看到，纤维在初始段内，因为没有受到气流的作用，保持着水平状态。但是，随着时间的增加，纤维开始出现弯曲变形。纤维首先从约束部分开始变形，然后延伸到纤维的中间部位，然后自由端开始接触喷嘴导纱管的下壁面，随着气压不断变化，纤维的自由端碰到下壁面后有一个向上变形的趋势，最后触碰到导纱管上壁面。纤维在t=1.582 ms时，纤维基本恢复到与初始相一致的状态，完成1个周期的运动。

为了定量分析纤维的波动变形情况，在纤维的边界上均匀地取17个坐标点，并且在以上6个时刻中取了3个时刻来分析这17个坐标点在z坐标轴上的位移，通过这17个点相对喷嘴中心轴线的距离来定量地分析纤维的弯曲变形情况。弯曲变形特性如图4所示。

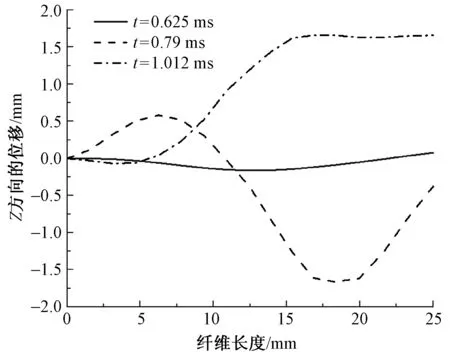
图4 纤维在3个时刻的波动情况Fig.4 Volatility of fiber at three moments

图4中每条曲线代表了不同时间点上纤维相对喷嘴中心轴线的距离。在最初的时间点上，纤维并没有明显离开喷嘴中心轴线的趋势，图上正方体模型曲线就代表了纤维最初的波动情况。

纤维左端被约束的区域附近并没有发生非常明显的弯曲变形。变形最大的区域是接近自由端的区域，从图4可看出，在这3个时刻纤维每个部位基本都存在弯曲变形，并且呈现三角正弦或者余弦波形式的波动。

纤维不仅在高速气流中会产生弯曲变形，也会产生拉伸和压缩变形。对纤维进行离散分析时将纤维表面用相同大小的等长单元尺寸来进行离散。在纤维约束端截取了一小段长度，一端受到约束条件的限制无法运动，另一个点可以在Y-Z平面上任意运动，截取的纤维段如图5所示。

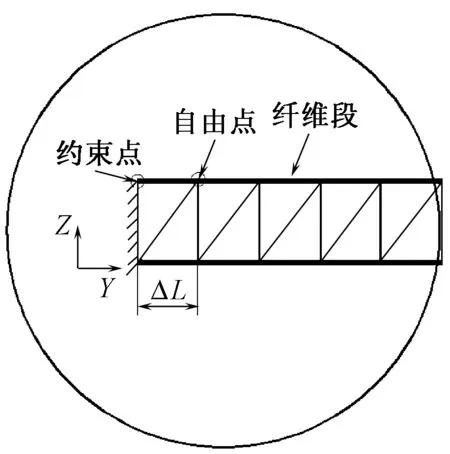
图5 纤维段上的约束点与自由点Fig.5 Constrained point and free point of fiber

分析自由点在Y轴上的运动情况，并且以约束点作为参考点，约束点任何时刻在Y方向上的位移都为0，而自由点不受约束，它在Y轴上的位移会随着时间的变化而发生变化。图6示出自由点和约束点在Y方向上随时间变化的情况。

图6 自由点和约束点在Y方向上的位移变化量Fig.6 Displacement variation in Y-direction of free point and constraint point over time

图6中虚线为约束点在Y轴上的位移变化量，实线为自由点在Y轴上的位移变化量。由于受到约束作用，约束点在任何时间点上都不发生任何位移变化，在图中表现为一条水平直线，即位移变化量为0；而对于自由点，在剪切力的作用下就会在Y轴上发生位移变化，正值代表伸长量，负值代表压缩量。显然相对图4纤维在Z方向上的位移变化量就可以看出，纤维的拉伸压缩量非常小。

3.2 纤维的受力特性

纤维受到的弯曲影响主要与纤维表面受到的主应力有关，而纤维受到的拉伸变形作用与纤维表面受到的切应力有关；因此，分析纤维在3个时刻上受到的主应力与切应力的分布。结果如表3、4所示。

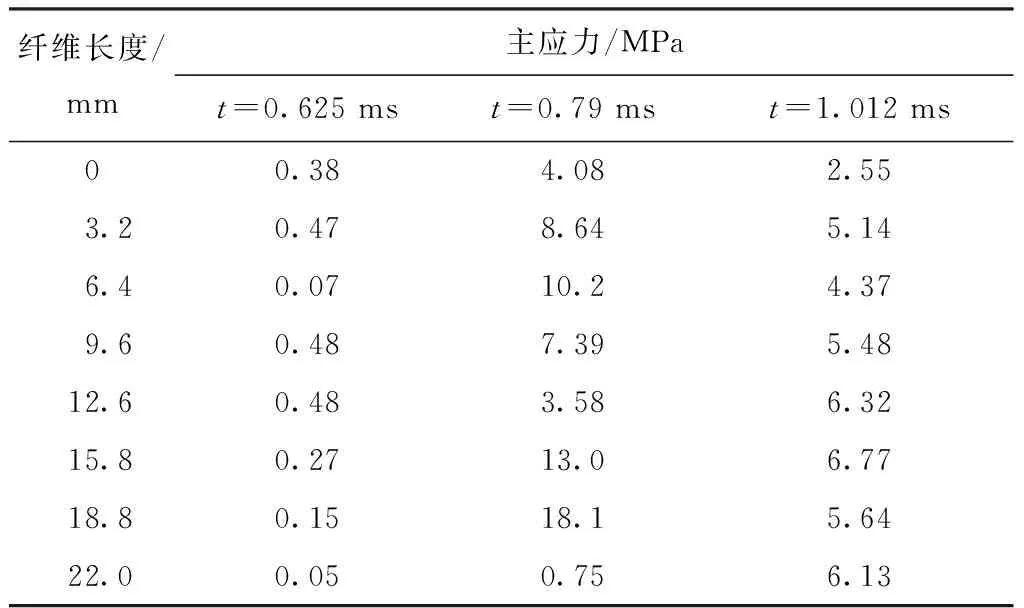
表3 3个时刻主应力在纤维上的分布

表4 3个时刻切应力在纤维上的分布

Tab.4 Distribution of shear stress in fiber at three moments

纤维长度/mm切应力/MPat=0.625mst=0.79mst=1.012ms00.202.351.453.20.283.402.096.40.035.532.279.60.254.042.9412.60.252.033.5015.80.146.653.7718.80.089.553.2122.00.030.433.43

从表3、4可以看出，在t=0.625 ms的时间上，受到的最大应力值都集中在纤维的中间部位，这与图3中t=0.625 ms时纤维的弯曲集中在中间位置符合一致，说明纤维在弯曲时受到的应力是最大的。在t=0.79 ms时，纤维受到2个应力的最大值均位于18.8 mm附近，而在图3中纤维在该区域正与壁面接触，说明纤维在与壁面接触时受到的应力也比较大，并且由于壁面对纤维的反作用力会使得纤维往反方向运动。在t=1.012 ms时，与图3比较可以分析纤维前半部分并没有发生明显的弯曲变形，该部分受到的应力相对稳定。

4 结 论

1) 修正纤维的本构方程可以得到纤维应力与应变对应的函数关系；在Arbitrary-Lagrangian-Eulerian坐标系下构建的纤维与气流耦合控制方程可以数值模拟纤维的弯曲变形。

2) 纤维在气流的作用下会产生弯曲、拉伸变形，约束端的纤维在气流中的弯曲变形不太明显；而自由端的纤维会产生明显的弯曲变形特性，并且呈现正弦或者余弦形式的波动。

3) 通过对纤维的受力分析可知，纤维受到应力最大的部分往往集中在纤维的弯曲部位和纤维与壁面接触部位。

4) 通过研究纤维的弯曲变形特性以及受力情况将有助于进一步研究流体动力型纺织机械的机制性。

[1] SMITH A C, ROBERTS W W. Straightening of crimped and hooked fibers in converging transport ducts: computational modeling[J]. Journal of Textile Research, 1994, 64(6): 335-344.

[2] KONG L X, PLATFOOT R A. Computational two-phase air/fiber flow within transfer channels of rotor spinning machines[J]. Journal of Textile Research, 1997, 67(4): 269-278.

[3] YAMAMOTO Satoru, MATSUOKA Takaaki. A method for dynamic simulation of rigid and flexible fibers in a flow field[J]. The Journal of Chemical Physics, 1993, 98(1):644-650.

[4] LINDSTRTIM SB, UESAKA T. Simulation of the motion of flexible fibers in viscous fluid flow[J]. Physics of Fluids, 2007, 19(11): 113307-1-16.

[5] TAKEMURA M, CHIBA K, NAKAMURA K. Motion of flexible fibers in a newtonian flow: part 2:evolution of the configuration of a single fiber in a simple shear flow[J]. Journal of Textile Engineering, 2001, 47(3): 77-91.

[6] TORNBERG AK, SHELLEY MJ. Simulating the dynamics and interactions of flexible fibers in Stokes flows[J]. Journal of Computational Physics, 2004,196(1): 8- 40.

[7] DONG S, FENG X, SALCUDEAN M, et al. Concentration of pulp fibers in 3D turbulent channel flow[J]. International Journal of Multiphase Flow, 2003, 29: 1-21.

[8] PEI Zeguang, YU Chongwen. Numerical study on the effect of nozzle pressure and yarn delivery speed on the fiber motion in the nozzle of Murata vortex spinning[J]. Journal of Fluids and Structures, 2011,27:121-133.

[9] 徐存强，冯志华，董腾中,等.气流引纬主喷嘴内气流速度与纬纱间摩擦因数的关系[J].纺织学报， 2013,34(11):147-150. XU Cunqiang, FENG Zhihua, DONG Tengzhong, et al. The relationship between friction coefficients of the weft yarns and velocity of the airflow in main nozzle during weft insertion[J]. Journal of Textile Research, 2013, 34(11): 147-150.

[10] 李翠玉,张义同,徐家福.机织物悬垂屈曲的数值模拟[J]. 天津大学学报，2007,40(1):46-50. LI Cuiyu, ZHANG Yitong, XU Jiafu. Numerical simulation of draping and buckling of woven fabric[J]. Journal of Tianjin University, 2007, 40(1):46-49.

[11] 汪静，金玉珍，胡旭东,等.基于Win CE的喷气织机人机交互系统设计[J]. 纺织学报，2010,31(7):122-126. WANG Jing, JIN Yuzhen, HU Xudong, et al. Win CE based design of human-machine interaction system for air-jet loom[J]. Journal of Textile Research, 2010, 31(7): 122-126.

[12] ZHANG Hou, KLAUS-JURGEN Bathe. Direct and iterative computing of fluid flows fully coupled with structures[J]. Computational Fluid and Solid Mechanics, 2001(1): 1440-1443.

[13] BATHE Klaus-Jurgen, ZHANG Hou. Finite element developments for general fluid flows with structural interactions[J]. International Journal for Numerical Methods in Engineering, 2004, 60:213-232.

[14] PANTUSO D, BATHE K J, BOUZINOV P A. A finite element procedure for the analysis of thermo-mechanical solids in contact[J]. Computers and Structures, 2000, 75: 551-573.

Numerical simulation on coupling of fiber and air flow

JIN Yuzhen, LI Jun, LIN Peifeng, WU Zhenyu

(FacultyofMechanicalEngineeringandAutomation,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China)

A two-dimensional model of fluid-structure coupling was set up based on the equation of the fiber and the fluid control. The consistent time integration and iterative coupling algorithm were used to solve the equation. The interaction of the fiber and the airflow in the main nozzle, such as the fiber motional, deformational characteristics and the force of the fiber, was analyzed. The results show that the fiber under airflow will come into stretching and bending deformation and present in the form of sine or cosine. The deformation effect of the free end of the fiber is more obvious than that of the restrained end. The maximum stress often occurred in the bending position as well as the part where the fiber contacted with the wall.

fluid-structure interaction; numerical simulation; fiber; adaptive mesh

10.13475/j.fzxb.201501015206

2013-12-02

2014-09-30

浙江省自然科学基金资助项目(LZ14E050004, LQ12A02002)；浙江理工大学流体工程技术创新团队资助项目(11132932611309)；浙江理工大学研究生创新研究项目(YCX13023)

金玉珍(1979—)，女，副教授，博士。研究方向为纺织装备流体传动。E-mail: gracia1101@foxmail.com。

TS 101.2

A