一种基于多轴工业机器人的非线性同步控制方法

储婷婷，刘延杰，韩海军

（哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江哈尔滨 150001）

一种基于多轴工业机器人的非线性同步控制方法

储婷婷，刘延杰，韩海军

（哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江哈尔滨 150001）

0 引言

目前，同步控制主要主要分为非耦合控制和耦合控制方式，非耦合控制主要有并行控制、主从同步控制和虚拟总轴控制。耦合控制主要有交叉耦合控制。随着同步控制技术的发展，在交叉耦合经典同步控制策略上又提出了偏差耦合控制和环形耦合控制。

近年来，交叉耦合控制技术广泛应用到多轴系统中。2003年Perez- Pinal等人提出适用于同步电机数目N＞2的偏差耦合控制策略［1］。Borensteint J将改进的耦合同步控制方法应用在四自由度的工业机器人控制系统中［2］。Sun D与Mills J K将交叉耦合控制方法应用于多机器人的协调运动中［3］。遗憾的是上述方法都需要设计空间轨迹轮廓模型来构建同步误差，从而使得控制算法较复杂，阻碍了其工程实现。张承慧等设计了一种基于最小相关轴数目的相邻耦合误差同步控制算法［4］，仿真结果改善了四轴控制系统的同步性能。Sun Dong等将传统的PD控制与交叉耦合算法相结合，成功应用于并联机器人的高精度控制系统中［5］。工程实际中多采用PD控制［6］，然而纵观现有的PD偏差耦合控制算法，大多数控制系统仍广泛采用传统的线性控制。六轴工业机器人是典型的不确定非线性机械系统，其动力学模型十分复杂，不容易获得精确的动力学参数，并且常规的线性PID控制难以抑制扰动。

由于耦合控制策略能有效地改善轴和轴之间的同步误差，这里提出了一种基于六轴工业机器人含位置误差和同步误差的非线性PD偏差耦合控制方法，该方法无需考虑精确的动力学参数。首先，基于IRB120教学型机器人，建立该机器人的动力学模型及Adams虚拟样机；其次，设计六轴工业机器人的非线性PD同步控制器；最后，利用Simulink与Adams联合仿真，通过与传统的轨迹跟踪控制方法对比分析，验证相同规划轨迹下不同控制算法的各轴同步误差和末端轨迹精度。

1 机器人动力学模型及虚拟样机

利用拉格朗日方法可以建立机器人的动力学方程，系统的拉格朗日方程为：

Ip是第i传动机构的转动惯量。

利用Solider Works建立机器人的三维模型，将模型导入到Adams中。建立各个关节的运动副及驱动，设置输入为各轴位移，输出为各关节相对旋转坐标轴产生的力矩，得到机器人虚拟样机。将虚拟样机模型导入到Matlab中，即可实现Simulink与Adams的联合仿真。

2 非线性PD偏差耦合同步控制器设计

2.1 最小相关轴的同步误差

对于6台电机的同步控制系统，每一轴的控制至少应该考虑与其相邻两个轴的状态，相邻两轴称为该轴的最小相关轴［5］。

对六自由度串联机器人控制目标可以定义为：

假设各轴的运动控制参数均经过了换算，位置指令r（k）具有了一致的参数，设第i轴的实际位置xi（k）相对于指令位置r（k）的跟随误差为ei（k），则定义各轴同步误差为：

将位置误差和同步误差结合起来，定义耦合误差为：

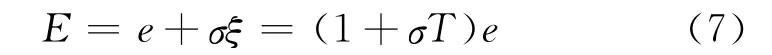
σ为耦合误差系数，

对于多轴同步控制系统，如果每一轴的控制仅仅考虑另外一轴的状态，这种控制结构易受负载扰动的影响。这里根据最小相关轴建立同步误差ξ，进而提高轴的同步性能。

2.2 非线性PID控制

设计一种较为简单的非线性函数，双曲余弦函数为：

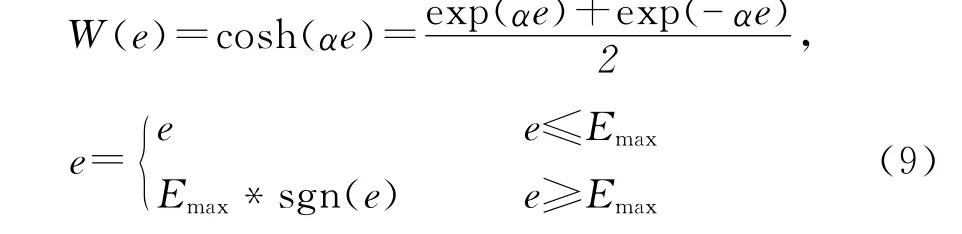
将伺服电机作被控对象，由机器人单电机模型的建立，可得出其为典型的II型系统，采用传统的Ziegler- Nichols规则整定固定增益的特征值为：Kr，＝8.34，Tr＝0.67T，从而得到PID控制参数为KP＝5；KI＝15；KD＝0.415；非线性函数的参数增益为α＝0.105；Emax＝6。

利用Simulink对线性PID和非线性PID的控制性能进行数值仿真，图1所示为两种方式的阶跃响应控制性能比较图。

图1 Simulink仿真得到的阶跃响应控制性能结果

由图1可知，固定增益PID控制的响应速度比非线性PID控制的响应速度慢得多，相对于线性PID控制，其过渡过程时间由0.95 s降到0.55 s，这种控制性能的显著提高正是由于非线性函数增益引起的。因此，这里提出基于饱和比例 微分（SPD）加位置同步误差的偏差耦合同步控制思想。

2.3 非线性PD偏差耦合同步控制

可将机器人的动力学模型式（2）整理成：

因此，该闭环系统具有全局渐进稳定性。

当机器人关节进行高速、高加速度轨迹跟踪时，为了避免不精确的动力学模型参数影响，可以通过速度和加速度前馈补偿来提高跟踪精度，设计机器人控制律中引入期望速度前馈参数km和加速度前馈系数KE，则机器人的关节偏差耦合控制律为

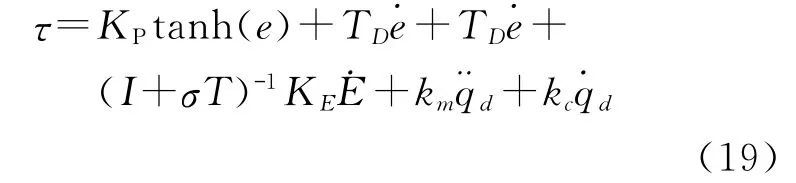
控制律的示意框图及简化的机器人结构控制框图如图2所示。

图2 机器人控制结构框图

3 基于虚拟样机的非线性PD偏差耦合控制实验

将Adams模型导入到Simulink仿真系统中，设定任意路径AB，其中起始点A（340，0，520）、终止点B（120，99，478）。设置A，B点的速度，加速度均为0，中间点的加速度为0，速度达到最大。利用五次多项式进行插值，每隔20 ms插值一次，所用时间为10 s。利用逆运动学得到各轴的运行轨迹，将各轴的实际运行角度通过正运动学求出末端的实际位置，与期望位置进行对比，验证轨迹精度。

采用非线性偏差耦合PD控制算法，仿真得到PD同步控制器参数分别为TD＝diag（0.4）；kc＝diag（3）；km＝diag（0.5）；KP＝diag（400）；KE＝diag（100）。（diag（·）表示对角矩阵）。为了验证上述的同步控制算法的控制效果，将其与传统非同步控制前馈加PD补偿算法和线性PD同步控制算法进行对比，仿真得到各轴运行轨迹如图3a所示，相邻两轴的同步误差如图3b所示。

图3 关节轨迹跟踪实验结果

图3a是期望的轴1的轨迹与3种方法的实际轨迹曲线，图3 b是轴1跟踪该轨迹产生的同步误差。关节1的轨迹跟踪误差如表1所示。

表1 关节1轨迹跟踪误差 rad

由表1所示关节1的轨迹跟踪实验结果可知，关节1的同步误差按照前馈＋PD反馈、PD同步控制、非线性PD控制的顺序误差逐渐递减。引入饱和非线性函数设计同步控制律后，系统的同步性能大大增强，相邻两轴的最大同步误差小于0.001 rad。

图4所示为3种方法下机器人实际运行轨迹与期望轨迹的轮廓空间曲线对比，分别比较末端夹手在笛卡尔空间下的及末端实际位置Px，Py，Pz与预期位置Px0，Py0，Pz0位置精度误差以验证轨迹精度。末端轨迹精度误差如表2所示。

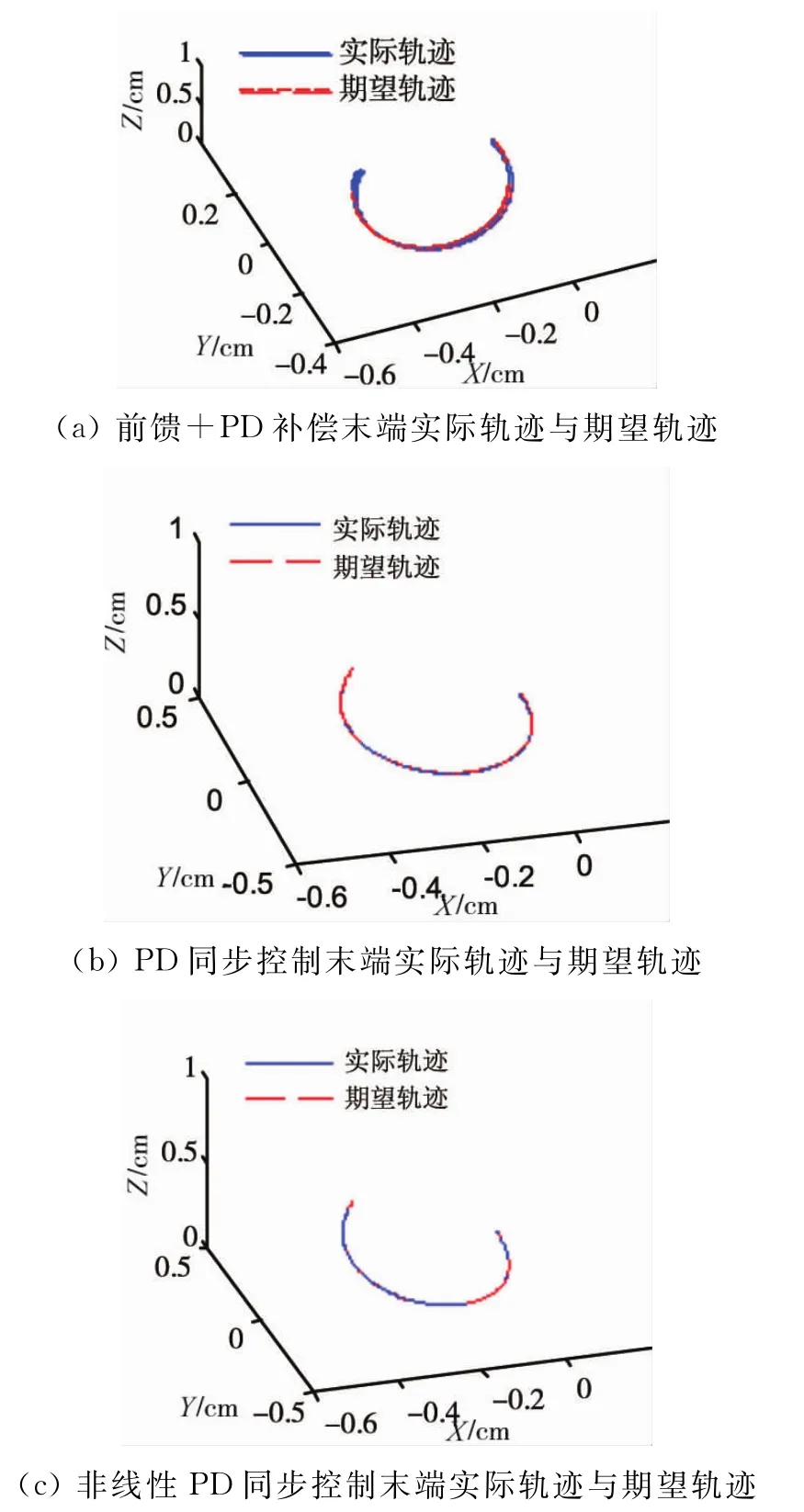
图4 3种方法下的轨迹精度对比

表2 末端轨迹位置误差比较 cm

由表2所示的末端轨迹误差比较可得，在相同的轨迹规划下，采用非线性同步控制策略，末端夹手具有较小的轮廓误差，轨迹精度达到0.1 mm以内。力矩前馈法中各个驱动电机是互相独立的，相邻两个关节的误差并不是以同样的速度收敛，而同步控制方法则是在该电机与其相邻两电机的误差间建立联系，将同步误差和位置误差共同作为附加的反馈变量，使每个电机的误差以更快的速度同步收敛，所以得到较小的同步误差。加入非线性环节后，控制器的调整时间缩短，同步性能变得更好。

4 结束语

为了提高多轴工业机器人轨迹跟踪精度，提高末端执行器的轮廓误差，在传统的PD偏差耦合同步控制算法的基础上，提出了一种基于六轴工业机器人包含位置误差和同步误差的非线性PD偏差耦合控制策略。建立了机器人soliderworks三维模型，并导入到Adams中得到虚拟样机，设计同步控制器，通过Simulink和Adams联合仿真验证不同控制方法下的轨迹精度。仿真结果表明，利用非线性PD同步控制方法得到机器人末端轮廓误差为0.1 mm；可以看出，加入非线性函数（tanh（·））后，大大减少了系统的调整时间，提高了六轴的同步性能，从而提高了末端执行器的轨迹精度。

［1］ Chuang H Y，Chang Y C.A novel contour error compensator for 3- PRPS platform［J］.Journal of Robotic Systems，2000，17（5）：273- 289.

［2］ Borenstein J.Control and kinematic design of multidegree- of freedom mobile robots with compliant linkage［J］.Robotics and Automation，IEEE Transactions on，1995，11（1）：21- 35.

［3］ Sun D，Mills J K.Adaptive synchronized control for coordination of multirobot assembly tasks［J］.Robotics and Automation，IEEE Transactions on，2002，18（4）：498- 510.

［4］ 张承慧，石庆升，程金.一种基于相邻耦合误差的多电机同步控制策略［J］.中国电机工程学报，2007，27（15）：59- 63.

［5］ Sun D，Shao X，Feng G.A model- free cross- coupled control for position synchronization of multi- axis motions：theory and experiments［J］.Control Systems Technology，IEEE Transactions on，2007，15（2）：306 -314.

［6］ Zhao D，Li S，Gao F，et al.Robust adaptive terminal sliding mode- based synchronised position control for multiple motion axes systems［J］.IET Control Theory＆Applications，2009，3（1）：136- 150.

A Nonlinear Synchronous Control Method Based on the Multiaxial Industrial Robot

CHU Tingting，LIU Yanjie，HAN Haijun
（State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150001，China）

为了提高机器人的末端轨迹精度，提出了一种基于六轴工业机器人的包含位置误差和同步误差的非线性PD偏差耦合控制策略。该策略无需考虑机器人精确的动力学模型参数，避免了不精确动力学参数的影响。首先建立了基于IRB120型虚拟样机的动力学模型，再利用Simulink和Adams进行联合仿真验证该策略的合理性。仿真结果表明，利用该方法与基于相同规划轨迹的传统非同步控制的力矩前馈算法和PD同步控制算法进行比较，有效地降低了关节同步误差，提高了末端的轨迹精度。

偏差耦合；非线性PD控制律；虚拟样机；轨迹精度

To improve robot trajectory precision，a nonlinear PD deviation coupling control strategy is designed which contains position error and synchronization error between said six axes.The strategy does not consider an accurate kinetic model for the robot as it is not needed；as a result，the impact of inaccurate kinetic parameters is avoided.First a kinetics model is established based on the IRB120 virtual prototype，then Simulink and Adams are used to conduct a joint simulation and test the appropriateness of the strategy.The simulation shows that，when based on the same planned trajectories，compared with traditional unsynchronized control of torque feedforward algorithm and the PD synchronization control algorithm，this strategy has reduced joint synchronization error.The joint trajectory precision is also improved.

deviation coupling；N- PD controller；virtual prototype；trajectory precision

TP24

A

1001- 2257（2015）08- 0072- 05

储婷婷 （1992－），女，安徽马鞍山人，硕士研究生，研究方向为工业机器人控制；刘延杰（1975－），男，黑龙江哈尔滨人，教授，研究方向为机器人技术与系统；韩海军（1985－），男，黑龙江哈尔滨人，博士生，研究方向为机器人传感技术与运动控制。

2015-04- 08

国家“863计划”项目（2013AA040901）；黑龙江省创新专项（YC13D004）