转子静偏心状态下机床电主轴电磁力有限元分析
王 锦,景敏卿,樊红卫,史必佳,刘 恒
(西安交通大学机械工程学院,陕西西安 710049)
转子静偏心状态下机床电主轴电磁力有限元分析
王 锦,景敏卿,樊红卫,史必佳,刘 恒
(西安交通大学机械工程学院,陕西西安 710049)
0 引言
高速机床需要高速主轴系统。电主轴正是在如此背景下发展并逐渐成为高速机床主轴系统的首选主轴[1]。由于电主轴实现了电动机与主轴转子的一体化,因此它是一种典型的电磁直驱装置。和普通工频电动机不同,机床电主轴的工作转速和动态回转精度要求更高,因此其振动尤其是电磁振动问题需要特别关注。然而,纵观已公开的文献可知,关于电主轴电磁振动的研究甚少。2011年,王丽艳[2]、王明权[3]先后针对陶瓷电主轴、空气静压电主轴探讨了电主轴不平衡磁拉力的计算问题。2012年,张丽秀[4]针对陶瓷电主轴电磁振动进行了更深入的研究。2014年,喻丽华[5]针对气浮电主轴开展了从磁拉力计算到电磁振动响应分析的研究。除此之外,国内外关于电磁振动的研究主要是针对一般电动机和发电机进行的[69]。根据对电主轴发展现状的调研,钢制球轴承支撑的磨削电主轴是当前国内应用较多的电主轴类型。因此,以此类电主轴为研究对象主要探讨电主轴工作状态下电磁力的频谱表现,特别是转子偏心工况下不平衡磁拉力的计算。研究工作为电主轴的电磁振动分析和低振动电主轴的设计提供理论参考。
1 电主轴及其电磁力波
1.1 电主轴设计参数
以洛阳轴研科技股份有限公司170MD12Y16磨削电主轴为研究对象,其额定功率为10 k W,额定转速为12 000 r/min,额定电压为350 V,额定电流为22 A。其电机采用恒扭矩三相异步电动机,转子导条采用鼠笼型结构。
1.2 电主轴气隙偏心下的电磁力波频谱
静偏心是电主轴转子偏心的常见情况,如图1所示,在电磁场上表现为气隙偏心。因气隙偏心会使气隙磁导发生变化,产生额外谐波磁场,这些谐波磁场和主波磁场、定转子绕组谐波磁场或者相互之间发生作用,有可能产生新的低阶次的电磁径向力,这样就会产生额外的电磁噪声,当偏心产生的噪声较大时可能影响电主轴正常运行。

图1 电主轴静偏心
根据参考文献[10- 11],极坐标下的气隙有效长度可以按照余弦规律表示为:
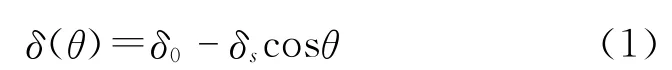
δ0为均匀气隙的长度;δs为气隙偏心的长度;θ为机械角位移。考虑气隙偏心,电机的气隙磁导可以近似表示为:
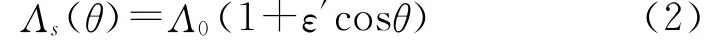
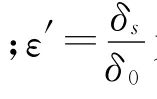
为相对偏心率。这里的ε′前用正号,是由于气隙减小磁导反而增加的缘故。
电主轴的气隙合成磁势可表示为:
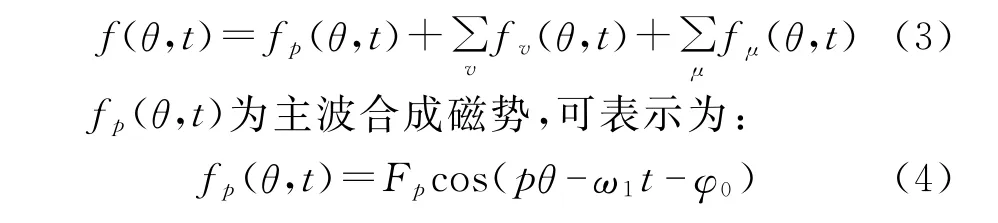
Fp为主波合成磁势的幅值;p为极对数;ω1为主波合成磁势的角频率;φ0为主波合成磁势的初相角。
fv(θ,t)为定子绕组v次谐波磁势,可表示为:
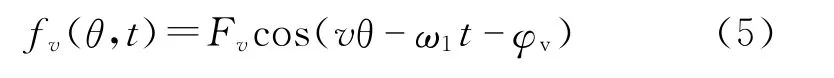
Fv为v次谐波磁势幅值;φv为v次谐波磁势初相角。由于齿谐波是绕组磁势中的最主要根源,因此在这里只关注齿谐波的次数,它的次数可表示为:

Fμ为μ次谐波磁势幅值;φμ为μ次谐波磁势的初相角;ωμ为μ次谐波磁势相对于定子的角频率。当转子导条采用鼠笼型转子时,由于相数较多,所以无相带谐波磁势,只有齿谐波磁势,该齿谐波的次数可以表示为:

前两者的角频率为ω1;后者为ωμ。
对于所研究的电主轴,极对数p=2,定子槽数为24,转子槽数为28。因此,极对数为μ-1的附加谐波和谐波磁场相互作用产生的力波次数和频率分别为:

根据上述三相异步电动机的电磁力波理论,由于气隙偏心,电主轴将产生次数为的次数较低力波引起的电磁振动。
2 电主轴电磁场有限元分析
2.1 电主轴二维电磁场有限元模型
为了计算电主轴定子上所受的电磁力及其频率分量,首先需要建立电主轴的有限元模型,电主轴有限元模型如图2所示。这里,选择Ansoft软件建立电主轴的二维有限元模型来对其内部的受力情况进行分析。首先,根据电主轴的基本参数在Ansoft RMxprt中生成2D几何模型,如图2a所示。然后,将几何模型导入Maxwell 2D瞬态模块进行有限元计算,分析模型如图2b所示。
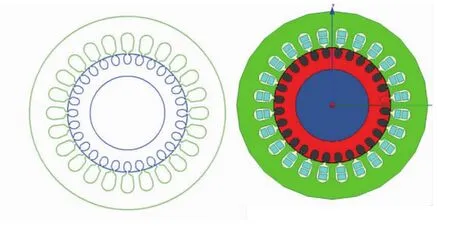
图2 电主轴有限元模型
2.2 电主轴主要性能曲线
对2D模型进行求解,可得电主轴空载性能曲线,如图3所示。
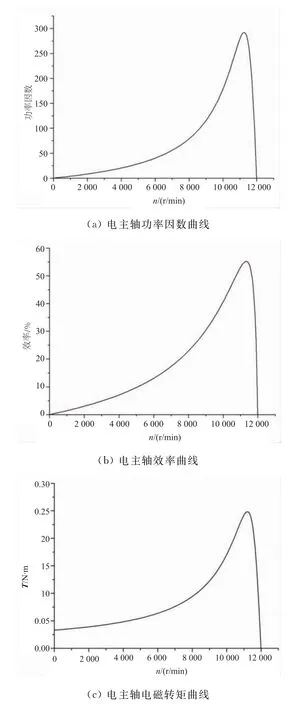
图3 电主轴主要性能曲线
由图3可知,电主轴工作情况正常,性能指标合格,证明所建模型是正确、有效的。
3 电磁力波有限元计算与频谱分析
3.1 非偏心工况下电磁力波分析
设电主轴的转速分别为2 700 r/min,3 300 r/min,3 900 r/min,4 500 r/min,对电主轴无偏心状况下电磁力和电磁力矩进行仿真,分析时间为250 ms,步距为0.2 ms。图4是电主轴在3 900 r/min时定子所受电磁力的频谱分析结果,由图可以看出,在1.56 k Hz处出现最大峰,这是定子绕组和转子绕组谐波磁场产生的力波频率。不同转速下,电主轴定子所受电磁力如图5所示(由于定子所受电磁力是一时变力,因此选取电主轴在50~250 ms内电磁力平均值作为定子所受电磁力)。从图5可以看出,在未发生偏心情况下,随着转速升高,电磁力反随之减小,与理论推导结果相符。由式(19)可知,因电主轴空载耗损功率主要是机械摩擦损耗功率,其值随转速升高基本不变。因此,定子所受力矩随转速升高而降低;同样,定子所受电磁力也随转速升高而降低,与转速成反比例关系为:
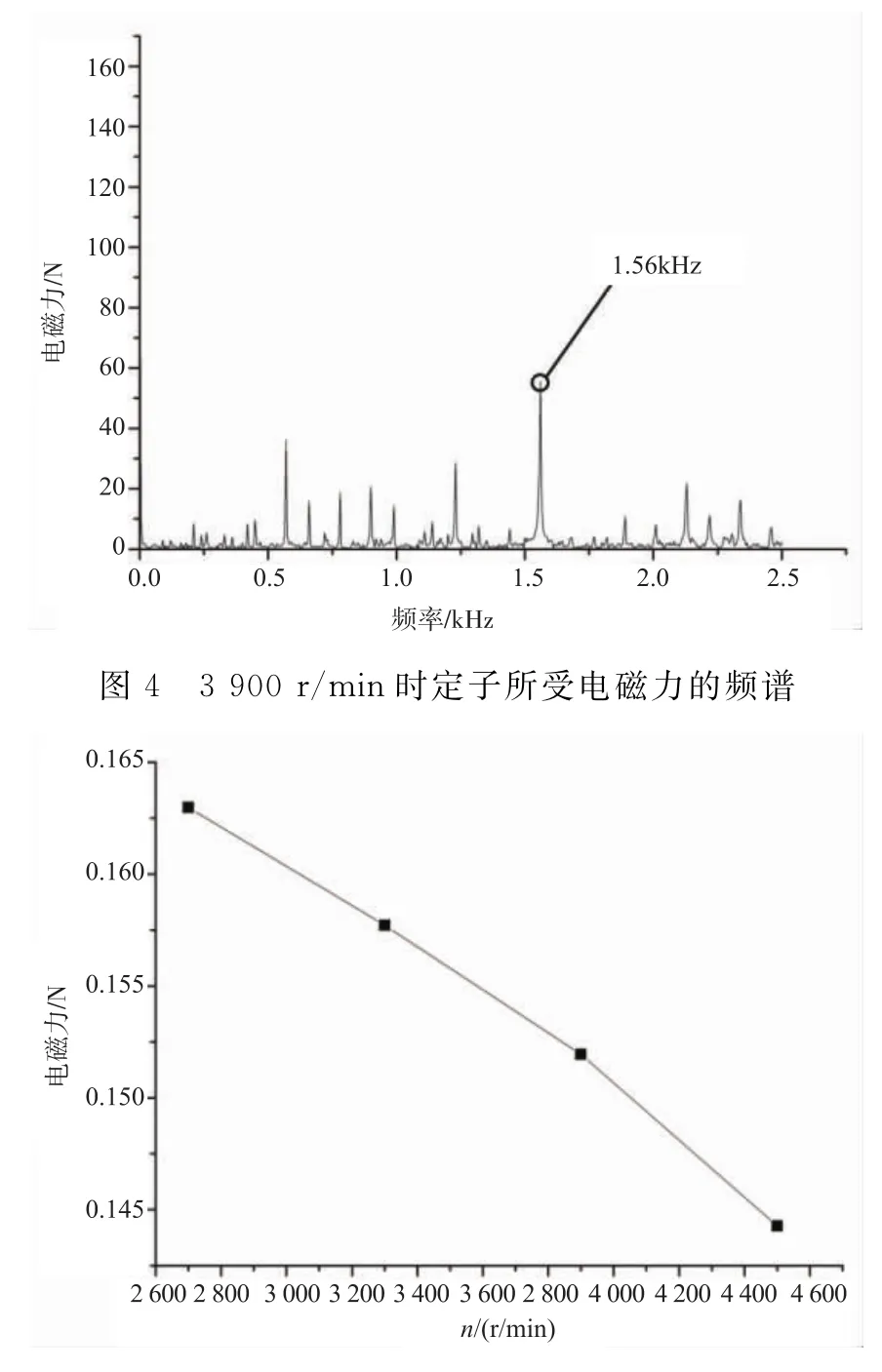
图5 不同转速下定子受到的电磁力

T为电主轴定子所受转矩;P为空载损耗功率;n为转速。
3.2 偏心工况下电磁力波分析
为了对电主轴在偏心状况下的电磁不平衡力进行分析,在电主轴定子位置不变的情况下,通过对电主轴转轴和转子Y向进行平移实现对电主轴气隙偏心的模拟。图6是电主轴分别在2 700 r/min,3 300 r/min,3 900 r/min,4 500 r/min转速下,从偏心0.01 mm直至增加到0.1 mm,其电磁力的变化情况。

图6不同转速下定子所受电磁力-偏心关系
由图6可以看出,在相同偏心下,转速越高,电主轴定子所受的不平衡磁拉力越小。在相同转速下,随偏心增大,电主轴所受不平衡磁拉力也增大。不过,可以看出整个过程分为3段,偏心量为0.01~0.03 mm时不平衡磁拉力增长曲线斜率较小,增加较缓慢;偏心量为0.03~0.05 mm时不平衡磁拉力增加曲线斜率明显增大,增长较第1阶段更快;偏心量为0.05~0.1 mm时不平衡磁拉力增加曲线斜率较第2阶段放缓,但较第1阶段快;说明第2阶段即偏心为0.03~0.05 mm时电主轴对偏心量最敏感。
图7为电主轴在转速3 900 r/min、偏心0.08 mm情况下定子所受不平衡磁拉力的频谱分布。由图可以看出,在频率1.56 k Hz(12f1)、1.82 k Hz(14f1)处频谱出现峰值,这与静偏心理论分析结果一致。
选取电主轴转速为3 900 r/min不同偏心下定子所受电磁力进行傅里叶变换,得到其在12f1及14f12个频率下的频谱分量的变化曲线图如图8所示。由图可以看出,随偏心量的增加12倍电源频率下的频谱分量一直增加,而14倍电源频率的频谱分量在偏心量为0.08 mm时达到最大值,之后随着偏心量的增加而减小。但是这两个频率一直是定子所受电磁力的主要频率分量,在不同偏心量下,12倍电源频率和14倍电源频率分量始终是定子所受电磁力的主要频率分量,证明之前的理论分析是正确的,当电主轴出现静偏心时,附加磁场产生的低阶力波是电磁力的主要频率分量。

图7 3 900 r/min,偏心为0.08 mm时定子所受电磁力频谱
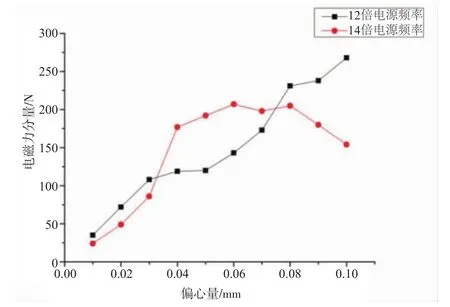
图8 3 900 r/min时,电磁力频谱分量 偏心示意
4 结束语
通过对某国产电主轴转子静偏心下电磁力的研究分析,得到如下结论:静偏心会在无偏心力波阶次基础上增加±3阶成分,产生在12f1和14f1力波频率。偏心丰富了力波阶次成分,同时其中阶次小的成分也相应增大了电磁力。随偏心的增大,电磁力增大,分别在偏心为0.01~0.03 mm、0.03~0.05 mm和0.05~0.1 mm 3个范围内成线性关系,当偏心为0.03~0.05 mm时,磁拉力增长幅度最大。12f1处电磁力分量随偏心量增加而增加;处电磁力分量先随偏心量增加而增加,14f1后当偏心量达到0.08 mm时达到最大值,此后随偏心量增加而减小。研究工作为转子偏心引起的电磁振动的抑制提供了理论支撑。
[1] 虞付进.电主轴技术的应用与发展趋势[J].机电工程,2003,20(6):71- 73.
[2] 王丽艳.陶瓷电主轴电磁力及损耗分析[D].沈阳:沈阳建筑大学,2012.
[3] 王明权,李战伟,贾月明.高速空气静压电主轴的振动及控制策略[J].电子工业专用设备,2011(11):46 -51.
[4] 张丽秀,吴玉厚,王丽艳,等.气隙偏心对陶瓷电主轴转子系统的影响[J].机械科学与技术,2012,31(9):1512- 1515.
[5] 喻丽华,谢庆生,李少波,等.高速气浮电主轴转子系统不平衡响应分析[J].重庆大学学报,2014,37(9):18- 25.
[6] 唐东炜,唐孝镐.异步电动机气隙不均匀引起的电磁力波的计算[J].中小型电机,2000,27(1):26- 27.
[7] 万书亭,李和明,李永刚.气隙偏心对汽轮发电机定转子振动特性的影响[J].振动与冲击,2005,24(6):21 -23
[8] 代颖,张千帆,宋立伟,等.抑制车用异步电机电磁噪声的槽配合[J].中国电机工程学报,2010,30(27):32 -35.
[9] 左曙光,张国辉,吴旭东,等.倾斜偏心下轮毂永磁同步电机电磁力分析[J].浙江大学学报(工学版),2015,49(5):902- 907.
[10] 陈世坤.电机设计[M].北京:机械工业出版社,1984.
[11] 陈永强.电机噪声的分析与控制[M].杭州:浙江大学出版社,1987.
Finite Element Analysis of Electromagnetic Force in Machine Electric Spindle With Rotor Eccentricity
WANG Jin,JING Minqing,FAN Hongwei,SHI Bijia,LIU Heng
(School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an 710049,China)
电磁振动是电磁直驱型机床电主轴不可回避的振动来源,为了抑制电磁振动需要探讨其电磁力的频谱特征。推导了三相异步电主轴的电磁力波计算公式,重点分析了转子偏心状态下的电磁力波特点。基于Ansoft电磁场计算软件,建立了某国产电主轴的电磁场有限元分析模型,获得了电主轴的运行特性曲线。研究了转子在不偏心和偏心状态下的电磁力频谱变化规律,结果表明,静偏心会使电磁力力波成分更为丰富;偏心的增加不会影响电磁力的阶次和频率分布,但与不平衡磁拉力的幅值和低阶力波幅值成正相关关系,将加剧电主轴的振动。
机床电主轴;电磁力;转子偏心;有限元分析;频谱分析
Electromagnetic vibration is an inevitable vibration source for an electric spindle;therefore,it is necessary to study the frequency spectrum of electromagnetic force in order to suppress electromagnetic vibration.The calculation formula about electromagnetic force of threephase asynchronous electric spindle was derived and the characteristics of electromagnetic force with rotor eccentricity was analyzed.An electromagnetic field finite element analysis model was built for a domestically produced electric spindle’s based on Ansoft software,and a main performance curve of electric spindle was obtained.The variation of electromagnetic force’s frequency spectrum with eccentricity and without eccentricity was researched and the results show that the electric spindle with eccentricity produces additional components of electromagnetic force.Increased eccentricity does not influence the order or frequency distribution of the electromagnetic forcebut the increase of eccentricity positively relates to the amplitude of electromagnetic force and low- order force.For this reason,the vibration of electric spindle will be exacerbated.
machine tool spindle;electromagnetic force;rotor eccentricity;finite element analysis;frequency spectrum analysis
TM301.4
A
1001- 2257(2015)08- 0033- 05
王 锦(1991—),男,湖南湘潭人,硕士研究生,研究方向为电主轴电磁分析与振动测试 ;景敏卿 (1956—),男,陕西咸阳人,博士,博士研究生导师,研究方向为现代测控理论与技术等。
2015-03-04
国家重大专项(2012ZX04001- 012- 04)

