选用多种计量标准器检测带表内卡规示值误差及其不确定度

黄伟城

(浙江省计量科学研究院，杭州 310008)



选用多种计量标准器检测带表内卡规示值误差及其不确定度

黄伟城

(浙江省计量科学研究院，杭州 310008)

为了确保带表内卡规的数据准确可靠，有必要将其纳入常规几何量的量值传递和溯源系统，根据带表内卡规的工作原理和计量特性，本文提出多种检测带表内卡规示值误差的方法和其不确定度验证。

检测方法 内卡规 内尺寸测量 示值误差 量块

0 引言

带表内卡规是一种实用性较强的专用测量内尺寸的量具，利用杠杆传动机构，将活动量爪测量面的摆动转变为指示表量杆的移动，并由指示表进行读数。带表内卡规主要用于内尺寸的测量，根据被测面的形状，带表内卡规的量爪的测头可以是平面、尖头和圆柱面，可用于测量工件孔径、内环形沟槽直径及台阶孔径等尺寸及其偏差，是一种通用型量具无法代替的检测工具。目前的国家校准规范JJF 1253—2010《带表卡规》规定用量块与量块内测量附件组成的内尺寸进行测量，但在实际工作中很多人用不同的方法进行检测，下面我根据不同的检测方法对比进行说明。

1 带表内卡规的检测方法实用性对比

例如，对于一只分度值为0.01mm，测量范围为75～95mm的带表内卡规，用量块和内尺寸测量专用检具组合、光滑极限量规、外径千分尺进行检测，这些检测方法从要求上都能满足对带表内卡规的检测，但从经济实用性上却存在很大的不同。

1.1 用外径千分尺检测带表内卡规示值误差

带表内卡规测量范围为75～95mm，外径千分尺测量范围为75～100mm作为主要标准器，价格为150元，所以只要配齐300mm以内的外径千分尺，所有的带表卡规都可以检测，外径千分尺价格便宜，保管也方便。

1.2 用光滑极限量规检测带表内卡规示值误差

带表内卡规测量范围为75～95mm，需75、80.2、85.5、90.7、95mm 5块光滑极限量规价格为2000元。但其他测量范围都不包括在内，配齐所有的光滑极限量规价格贵，对于一般的企业和计量技术机构难度比较大，保管也不方便。

1.3 用量块与内尺寸测量专用检具组合检测带表内卡规示值误差

2级83块组量块价格为2700元，内尺寸测量专用检具价格为2500元，共合计5200元，测量范围在200mm以内的都能校准到，量块价格贵，保管也不方便。

1.4 用专用夹具检测带表内卡规示值误差

有些企业自做专用夹具来校准带表内卡规的示值误差，但它不属于计量器具，没有办法进行计量溯源，所以也行不通。

2 用外径千分尺检测带表内卡规示值误差的方法

带表内卡规的测量面直径为φ3mm，外径千分尺测量面的直径为φ6.5mm，也就是说带表内卡规的测量面直径为φ3mm在外径千分尺两测量面之间上下和左右只能移动3.5mm来找转折点，从检测方法上看，3.5mm的距离能够使检测的数据准确、可靠。浙江省计量科学研究院在这几年检测带表内卡规中，用外径千分尺校准带表内卡规中积累大量实践经验，认为外径千分尺校准带表内卡规的方法可行，广大计量同行均可验证，用外径千分尺检测带表内卡规示值误差时的示意图如图1所示。

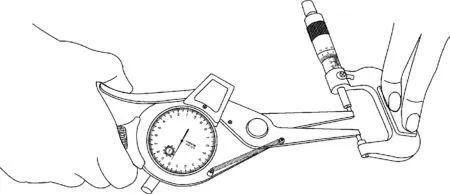
图1 用外径千分尺检测带表内卡规示值误差时的示意图

3 用量块和光滑极限量规及外径千分尺对带表内卡规不确定度的验证

3.1 概述

3.1.1 测量方法：依据JJF 1253—2010《带表卡规校准规范》。

3.1.2 环境条件：温度(20±5)℃，相对湿度不超过80%。

3.1.3 测量对象:带表内卡规，测量范围为75～95mm。

3.1.4 测量标准:光滑极限量规、外径千分尺及量块与内尺寸测量专用检具组合。

3.1.5 测量过程:测量时，用两测量面直接接触量块或光滑极限量规或外径千分尺调整零位。用量块或光滑极限量规或外径千分尺进行检测。检测时，将带表内卡规的两测量面测头与量块或光滑极限量规或外径千分尺测量面接触，通过转动找到转折点时，带表内卡规示值与量块或光滑极限量规或外径千分尺尺寸之差，即为带表内卡规的示值误差。

3.1.6 目标不确定度UT：根据JJF 1094—2002《测量仪器特性评定技术规范》中5.3.1.4的规定，评定带表内卡规示值误差的扩展不确定度U(k=2)与其示值最大允许误差的绝对值MPEV之比，应小于或等于1:3，即：

由上式可以得到与校准规范技术要求相对应的目标不确定度UT见表1。

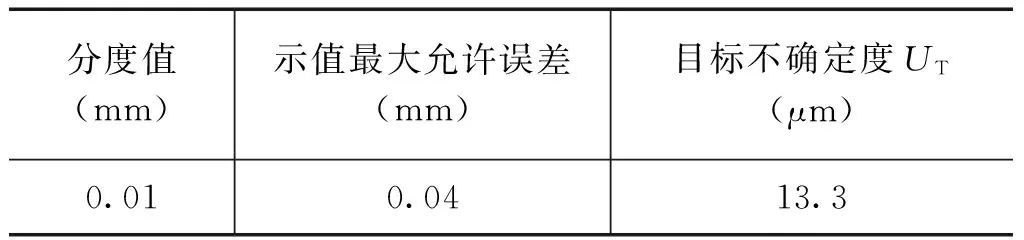
表1 目标不确定度UT

3.2 测量模型

e=Lc-Lb+Lcac·Δtc-Lb·ab·Δtb

(1)

式中：e为带表内卡规的示值误差，mm；Lc为带表内卡规的示值(20℃条件下),mm；Lb为量块或光滑极限量规或外径千分尺的长度(20℃条件下),mm；ac，ab分别为带表内卡规和量块或光滑极限量规或外径千分尺的线膨胀系数，℃-1；Δtc，Δtb分别为带表内卡规和量块或光滑极限量规或外径千分尺偏离标准温度20℃的值，℃。

3.3 相关性和灵敏度系数

由于Δtc和Δtb基本是采用同一只温度计测量而具有相关性，其数学处理过程比较复杂，为了简化数学处理过程，需要通过如下方法将相关转化为不相关。

令δa =ac-ab，δt=Δtc-Δtb

由公式(1)就得到如下示值误差的计算公式：

e=Lc-Lb+LcacΔtc-LbabΔtb

=Lc-Lb+Lc(δa +ab)Δtc-LbabΔtb

=Lc-Lb+LcδaΔtc+LcabΔtc-LbabΔtb

(2)

因Lc、Lb非常接近，故以量块标称长度L替代式(2)中部分Lc、Lb，简化公式；同理，以a 替代ac、ab；以Δt替代Δtc、Δtb，得

e=Lc-Lb+L·δa ·Δt·+L·a ·δt

(3)

由公式(3)可以看出，各变量之间彼此不相关

灵敏系数：c1=∂e/∂Lc=1，c2=∂e/∂Lb=-1

c3=∂e/∂δa =L·Δt，c4=∂e/∂δt=L·a

由于各分量彼此独立，按不确定度传播律公式，其输出量估计值e的方差为

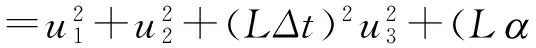
(4)

3.4 不确定度来源分析

1)带表内卡规重复性引入的不确定度分量u1；2)带表内卡规与量块或光滑极限量规或外径千分尺引入的不确定度u2；3)带表内卡规与量块或光滑极限量规或外径千分尺间线胀系数引入的不确定度u3；4)带表内卡规与量块或光滑极限量规或外径千分尺间温度差引入的不确定度u4。

标准不确定度一览表如表2。

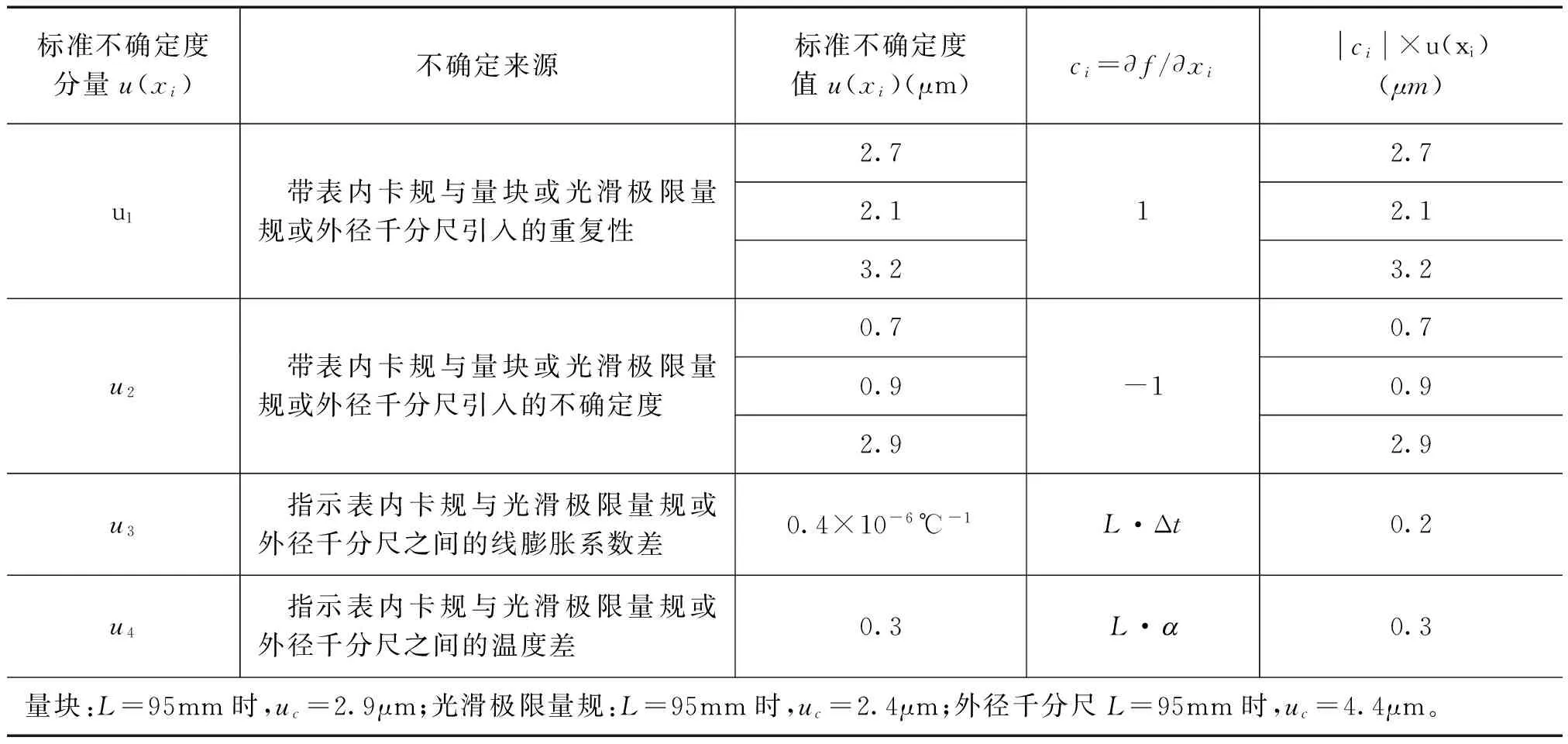
表2 标准不确定度一览表

3.5 标准不确定度分量的说明和计算

3.5.1 测量重复性引起的标准不确定度分量u1

选用75～95mm的指示表内卡规，选取95mm为校准点在重复性测量条件下，以外径千分尺作为主要标准器为例连续测量10次，得到测量列如表3所示。

表3 单次测量值 单位:mm

实际测量情况，在重复条件下连续测量3次，以该3次测量值的算术平均值为测量结果，可得到

同理可得：用量块与内测量附件组合作为主要标准器得到：u1=2.7μm；用光滑极限环规作为主要标准器得到：u1=2.1μm。

3.5.2 量块或光滑极限量规或外径千分尺引起的标准不确定度u2

1)根据JJG 146—2011《量块》规定，5等量块中心长度的测量不确定度：

U99=0.5μm+5×10-6ln，估计为正态分布，对应99%置信区间的包含因子k=2.6,故:

L=95mm时，5等量块测量不确定度为，u2=0.5μm+5×100mm/2.6=0.7μm。

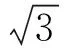
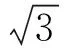
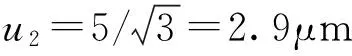
3.5.3 指示表内卡规与光滑极限量规或外径千分尺之间的线膨胀系数差u3

由于材料性质的差异，两种材料热膨胀系数界限在(11.5±1)×10-6/℃的范围内服从等概率分布，则δa 的区间半宽为1×10-6/℃，服从三角分布，测量尺寸为L，偏离标准温度的范围是±5℃，校准点的标准不确定度计算如下：

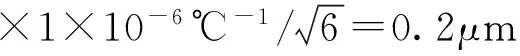
3.5.4 指示表内卡规与光滑极限量规或外径千分尺之间的温度差u4

指示表内卡规与量块或光滑极限量规或外径千分尺之间存在温度差，以等概率落于区间±0.5℃内任何处服从均匀分布，其区间半宽为0.5℃，测量尺寸为L和线膨胀系数11.5×10-6/℃-1，校准点的标准不确定度计算如下：

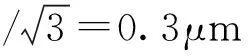
3.6 合成标准不确定度uc

量块:

光滑极限量规:

外径千分尺:

3.7 扩展不确定度U

取k=2,扩展不确定度如下：

量块:

U=k·uc=2×2.9μm=5.8μm

光滑极限量规:

U=k·uc=2×2.4μm=4.8μm≈5μm

外径千分尺:

U=k·uc=2×4.4μm=8.8μm

由此可见，用量块和光滑极限量规及外径千分尺校准带表内卡规示值误差符合测量不确定度合格判据U≤UT，本测量方法可行。

4 结论

综上所述，用外径千分尺作为计量标准器来检测带表内卡规的示值误差价格最便宜，保管方便；用光滑极限量规和量块作为计量校准器来检测带表内卡规的示值误差价格最贵，保管也不方便。所以用外径千分尺作为主要标准器这种检测方法有效，并且该方法操作简便、效率极高，从经济角度讲是一种最佳的检测方法，可作为计量技术人员检测带表内卡规的技术参考依据。

[1] 国家质量监督检验检疫总局.国家计量校准规范JJF 1253—2010《带表卡规》[S].中国计量出版社,2010

[2] 国家质量监督检验检疫总局JJF 1071《国家计量校准规范编写规则》[S].中国计量出版社,2011

[3] 中国计量科学研究院.JJF 1059.1—2012《测量不确定度的评定与表示》[S].中国计量出版社,2012

[4] 中国计量科学研究院.JJF 1011—2011《通用计量术语及定义》[S].中国计量出版社,2011

[5] 黄伟城.轮胎花纹深度尺检测方法及测量不确定度评定.计量技术，2013(12)

10.3969/j.issn.1000-0771.2015.11.16