回归分析在测力环校准中的研究
周亦泉 王福泉 何济泉
(广东省肇庆市质量计量监督检测所,肇庆 526060)
回归分析在测力环校准中的研究
周亦泉 王福泉 何济泉
(广东省肇庆市质量计量监督检测所,肇庆 526060)
运用回归分析中散点图和相关系数的方法确定测力环的负荷和百分表示值的相互关系,建立数学模型,采用最大似然估计法对数学模型的各个参数进行求解,获得与已知数据相匹配的最佳函数方程,最后对回归函数进行有效性分析,证明回归函数能够很好地达到预测效果。
回归分析;测力环校准;最大似然估计法;有效性分析;显著性检验
0 引言
测力环作为常用仪器,经常用于公路、铁路工程项目的试验中,它适用于公路土基、底基层材料等各种路面材料强度的试验。在测力环的校准工作中,我们一般按照规程的要求选择特定的校准点进行测量。在实际工作中,工程技术人员使用测力环对路面材料强度进行试验,得到的试验结果是百分表的示值(即变形量),而工程技术人员需要的试验数据是百分表示值对应的力值,如果这个示值并不是校准点中一个,那么研究获得校准点以外的力值就显得非常有必要了。我们可以通过对校准的数据进行回归分析,获得相匹配的回归函数,就可以对校准点以外的力值进行预测,以获得最佳效果。
1 测力环的校准和测量数据
在实际的测力环校准工作中,依据JJG 455—2000《工作测力仪》检定规程的要求,我们使用标准数显测力仪对测力环进行测量,测力环校准时一般安装固定在一个工作试验台上(如路面材料强度测力仪工作台等),校准时不要使用工作试验台本身的电动装置来施加压力,因为电动装置的加荷速度不好控制,加荷速度过快会导致仪器的物理性损坏,而且读数也不准确,所以我们另外配置了一个手动液压千斤顶作为加荷装置。
把手动液压千斤顶放在测力环正下方,两者的距离要略大于标准数显测力仪的高度,然后把标准数显测力仪平稳地放在千斤顶的上面,手动对千斤顶施加压力,当标准数显测力仪和测力环刚接触到(标准数显测力仪开始有力值显示)时,开始缓慢平滑地手动对千斤顶施加压力,仔细观察标准数显测力仪的力值(即测力环负荷)与测力环的百分表行程示值,读取两者对应的数据,得到一组测量数据对(xi,yi)。以量程为7.5kN的测力环为例,测量数据如表1,其中yi为标准测力仪的力值,xi为测力环百分表的示值。

表1 测量数据对(xi,yi)
针对上述测量数据,我们下面将采用数理统计的回归分析方法求解得到回归函数。
2 回归分析原理和内容
回归分析的原理是利用数据统计学的原理,通过数学方法对测量数据进行分析推导,研究确定变量之间的内在关系,建立变量的回归函数,通过回归函数推断未知变量。
回归分析的内容和步骤:从一组数据出发,画出数据的散点图,判断变量之间的相关性;根据变量之间的关系建立回归模型,求解回归系数,求解回归系数采用的数学方法有很多种,常用最小二乘法,最大似然估计法等;对求得的回归函数进行有效性检验;利用所求的回归函数进行预测。下面我们按照回归分析的步骤分步来进行。
3 测力环的测量数据对(xi,yi)的相关性
要确定回归函数的数学模型,我们首先要分析表1中的数据对(xi,yi)的内在关系,也就是它们之间的相关性。
依据表1的测量数据(xi,yi)画出相关图(又称散点图),具体做法如下:用直角坐标系的x轴代表自变量xi,y轴代表因变量yi,将表1的测量数据用坐标点的形式描绘出来,以此来描述相关点分布状况,从而得到观测数据对(xi,yi)的散点图,如图1所示。
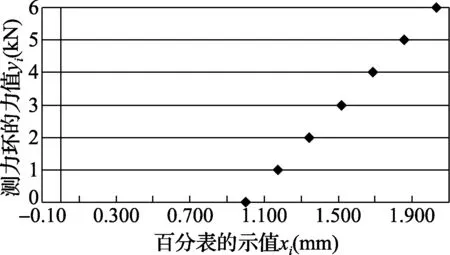
图1 测力环测量数据的散点图
由图1可以很直观地看出,测量数据对应的坐标点几乎在同一条直线上,而且yi随着xi的增大而增大,由此可见它们是高度正相关。
同时,我们也可以通过计算(xi,yi)之间的相关系数定量衡量两个随机变量xi和yi相互依赖的程度,进一步分析数据对(xi,yi)潜在的内部关系。
根据相关系数的定义,它等于两个变量xi和yi的协方差除以各自方差之积的正平方根,所以数据对(xi,yi)的相关系数r(xi,yi)为:
(1)
式中s(xi)为样本xi的标准偏差,公式为:
(2)
s(yi)为样本yi的标准偏差,公式为:
(3)
s(xi,yi)为样本协方差,公式为:
(4)
由表1的测量数据可以求出,s(xi)=0.370562,s(yi)=2.160247,s(xi,yi)=0.8005,所以r(xi,yi)=0.999994,根据数理统计学,如果r(xi,yi)大于0.8,则说明xi和yi是高度正相关,yi会随着xi的增加(减少)而增加(减少),(xi,yi)分散在一条上升的直线附近。
我们从描绘的散点图和求解相关系数的结果可以看到,测量数据对xi和yi是高度相关,(xi,yi)会分散在一条直线附近,这条直线称为回归直线,同时说明测力环负荷和百分表行程具有良好的线性关系,完全满足一元线性回归方程模型,所以我们可以建立一个一元一次的回归模型。
4 建立回归模型和最大似然估计法
4.1 建立回归模型
从上面的实验数据的相关性分析知道,测力环负荷和百分表行程具有线性关系,所以对应的函数为一元一次函数方程,我们可以假设回归函数模型如下:
Y=a+bx+ε
(5)
其中a为截距,b为斜率,都是未知参数,ε~N(0,σ2)属于随机误差。σ2越大表示随机误差越大,可以通过求解平方和分解公式进行估算。在这里如何求解a、b是关键,在数理统计学中可以采用多种数学方法分析推断未知参数a、b,如最小二乘法、最大似然估计法等,下面我们用最大似然估计法来求解参数。
4.2 最大似然估计法
取x的n个不全相同的值x1,x2……xn作独立试验,得到一组测量数据(x1,Y1),(x2,Y2)……(xn,Yn),其中Y1,Y2……Yn也是独立的,则得到基于Y1,Y2……Yn的似然函数:
(6)
在数理统计学中,L取最大值时,a、b取值为最大似然估计。显然这里L要取最大值,就要令式(7)中的平方和为最小:
(7)
我们知道,当Q关于a,b的偏导数同时等于0时,Q为最小值。所以,下面方程组成立:
(8)
通过求解上述方程组,可以得到a,b的最大似然估计:
(9)
其中:
(10)
测力环的回归方程的参数可以用上面的原理来推导出来,根据上面的测量数据可知,n=7,为方便计算回归函数的参数,我们可以做一个详细直观的列表,如表2。
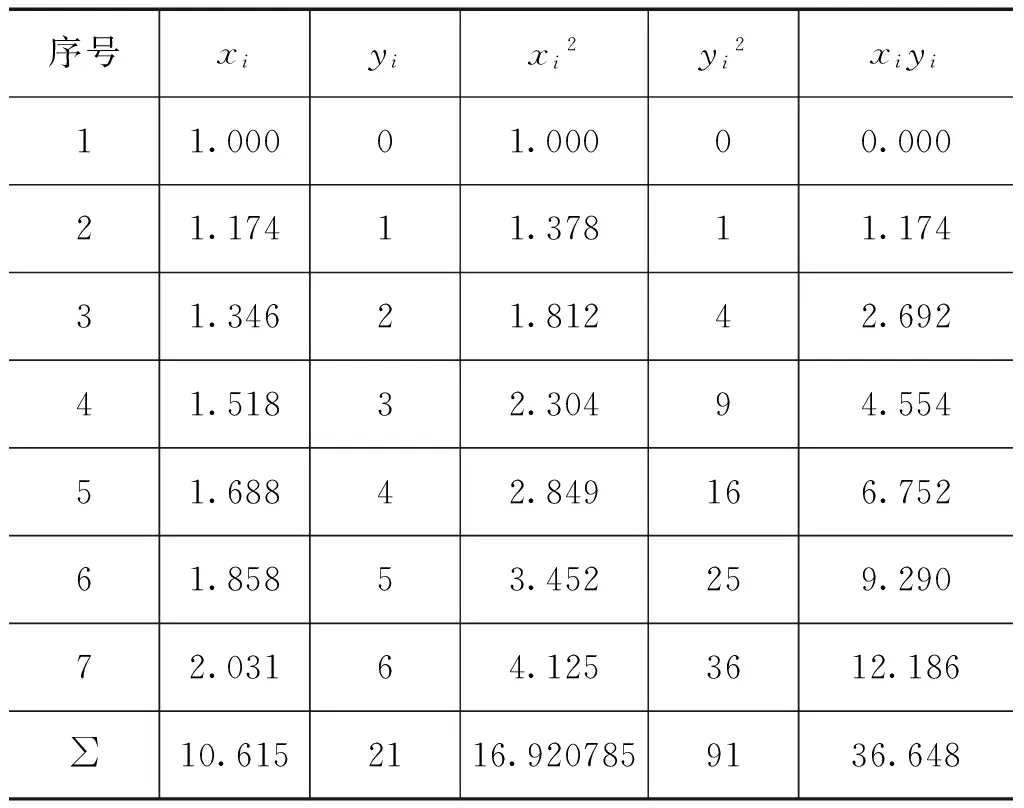
表2 回归函数的参数
由表2得:
所以得到:
10.615×5.829621=-5.840204
于是得到回归函数为:
y=-5.840204+5.829621x
上面得到的回归函数是从测量数据出发分析,是一元线性回归的经验公式,它是否有效及其可信程度,即回归函数对数据的预测是否有效可用,必须从以下方面进行检验评估,包括线性假设的显著性检验、回归函数拟合效果和Y的观测值的预测效果等方面进行评价。
5 回归函数的有效性分析
5.1 线性假设的显著性检验
若回归方程的线性假设需要符合实际,则参数b应不为零,因为b=0,则y不依赖于x。因此我们检验假设:
(11)
我们采用t检验法进行检验,根据数理统计学的有关推断得到:
H0:b=0的拒绝域为:
(12)
要对式(12)进行求解,首先需要对σ2进行估算求解。
5.1.1σ2的估算
通过估算σ2的大小可以评估获得的回归函数有效性,σ2越小,表示回归函数y=a+bx作为Y的近似导致的均方误差就越小,也就是说观测数据偏离回归方程的程度越小,同时说明得到的回归函数越有效。在数理统计中通过求解平方和分解公式得到σ2:
下面我们对上面根据测力环的测量数据得到的回归函数进行σ2的估算,由表2得到:

5.1.2 检验回归效果是否显著(取a =0.05)
由上面可知,σ2=0.000066,σ=0.00812,Sxx=0.823896,则式(12)中:
=651.659
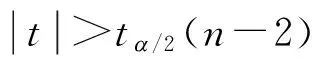
5.2 回归函数拟合效果的分析

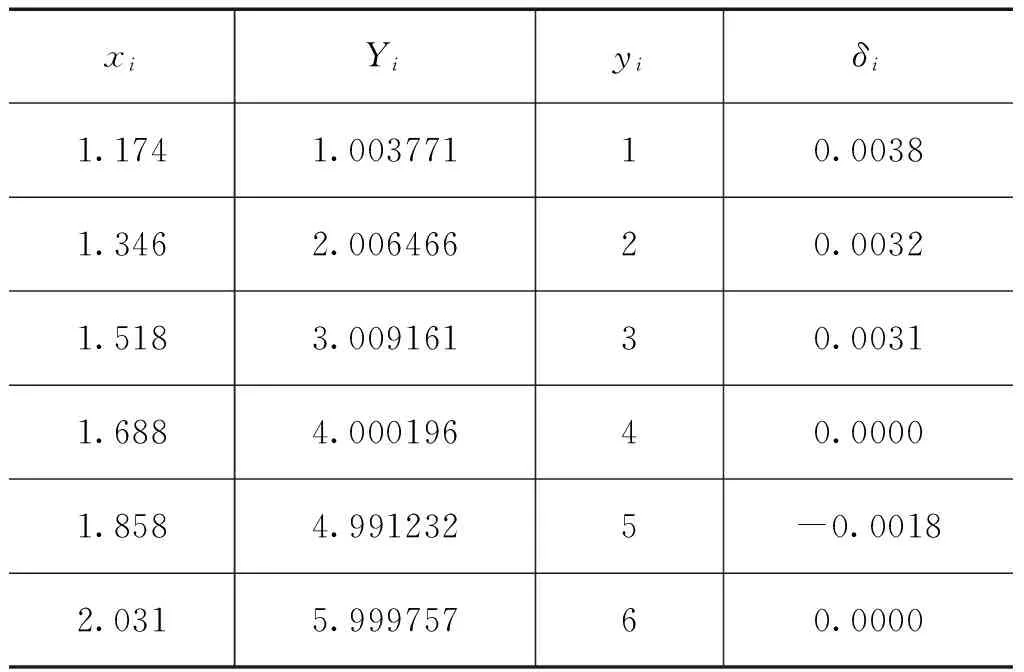
表3 回归函数拟合效果
由表3可知,用回归函数计算出来的结果与测量值相对误差均小于1%,符合有关规程的要求,拟合效果很好。
如果回归函数的回归效果不显著或拟合效果不好,可以分段进行回归拟合以达到最佳的效果。
5.3Y的观测值的预测及效果验证
如果我们对x=xi时对应Y的观测值Yi感兴趣,但是我们没有x=xi处的实际测量数据,这时可以利用回归方程获得xi对应的Yi。例如,当工程人员使用测力环工作时,得到的百分表的示值xi,而这个点并不在上面的测量数据中,这时就可以使用回归方程获得xi对应的测力环的力值yi,也就是使用回归方程对Y的观测值进行预测。
下面我们做一个试验,把回归方程对Y的观测值进行预测得到的值Yi和我们实测的值yi进行比较验证。我们按照测力环的校准方法,给测力环施加一个压力,这时测力环百分表的示值为1.325mm,标准数显测力仪显示的力值yi为1.879kN,则:
Yi=a+bxi=-5.840204+5.829621x
=-5.840204+5.829621×1.325
=1.884044kN
=0.27%
从相对误差δi的结果可以看到,预测的效果非常满意,回归函数的拟合效果很好。
6 小结
利用回归分析方法对测力环的校准数据进行统计分析,获得的回归函数是对测力环的荷载和百分表行程之间关系的最佳拟合,可得到与实际更为接近的测力环结果,为有关实验室的检测试验提供了较高精度的数据处理方法,有效地扩展测力环的测量范围,并提高现有仪器的使用效率。实践证明,测力环回归方程具有较高的应用价值,具有较好应用前景。
[1] 盛骤,等.概率论与数理统计.第4版.高等教育出版社,2008
[2] 何书元.概率论与数理统计.高等教育出版社,2006
[3] 麻青春,钱武威.基于最小二乘法的测力环线性回归分析与检验.交通标准化,2009(15)
[4] 朱林,李志峰,何建新,毛勤卫.基于MATLAB的应力环校准方程线性回归分析.计量技术,2013(8)
[5] 潘思曦,简卫平.回归分析法在电路检验中的应用.计量技术,2009(7)
10.3969/j.issn.1000-0771.2015.11.20

