新型二级频标驯服保持系统*
张雪萍 周 渭
(西安电子科技大学281信箱,西安 710071)
新型二级频标驯服保持系统*
张雪萍 周 渭
(西安电子科技大学281信箱,西安 710071)
提出了一种基于GPS的新型二级频标驯服保持系统。采用了将直接计数法和时间-幅度转换法相结合的一种高精度的短时间间隔测量方法,将该方法应用于GPS的1PPS信号和二级频标分频产生的1PPS信号之间的短时间间隔测量,秒级范围内可达到100ps测量分辨率。对时间间隔测量数据进行以消除相位抖动的Kalman滤波处理,经PID控制算法算出后的频率校正量,再通过高分辨率DAC和相应的信号调理电路去控制实现二级频标的精密驯服和保持。结果表明,利用该技术VCOCXO长期平均频率准确度驯服后可达到4.3×10-13,保持状态下可达到3.8×10-11。
二级频标;驯服和保持;Kalman滤波;PID控制器
0 引言
近年来,国内对基于GPS的时频标准的研究,不但克服了主要集中在电力网同步系统方面做研究的缺限,而且解决了精度和稳定性都不是很好的问题[1]。开始重视来自GPS卫星的1PPS的偶然跳变和失效情况,并提出相应的滤波算法来剔除粗大误差,结合锁定状态下存储的历史数据和相应的预测算法来实现一定时间内锁定精度的保持[2]。国外对基于GPS的晶振驯服技术也有很多研究,但是实现复杂度都很高[3]。在现代的测量和控制系统中,频率标准作为关键部件,其性能指标直接决定了测量和控制的精确度。GPS系统中的星载原子钟就扮演着这样的角色。一级频标长期稳定度和准确度很高,但是其价格昂贵;二级频标的价格便宜,但长期稳定度和准确度却大不如一级频标。为了获得一种其长期稳定度和准确度接近一级频标,价格却和二级频标相当的频率标准,本文提出了一种基于GPS的新型二级频标驯服和保持系统。
GPS的定位定时[4],接收到四颗或者更多GPS卫星信号,就能够准确地进行定位和授时。即利用GPS接收机,收到并产生长期准确度和稳定度较高的1PPS信号,但其带有一定的随机抖动。高精度时间间隔测量仪对GPS接收机输出1PPS信号与晶振或铷原子频标分频得到的1PPS信号之间不同步部分的时间间隔值进行测量,而后用相应的滤波算法对测量值进行数字滤波,得到相应的时间间隔差值ΔT,结合相邻两次测量值之间的采样时间t ,用测频差公式[5]:Δf/f0=ΔT/t 计算出频率偏移量Δf,再结合晶振或铷原子频标的压控灵敏度系数,利用相应的算法计算出应该加到晶振或铷原子频标上的压控电压所对应的数字量,进而通过高分辨率的D/A转换器输出该控制电压,达到校正晶体振荡器或铷原子频标输出频率的目的,使晶振或铷原子频标的振荡频率锁定在GPS时钟上。同时,在GPS工作正常并且系统达到锁定状态时,系统自动记录铷原子频标的校准数据和对应的时间等信息;从而可以在GPS信号丢失时,结合历史信息,运用算法,获得晶振或铷原子频标的对应校正量,实现在GPS信号失效后200min之内晶振或铷原子频标输出仍然能够保持一定的精确度。
1 系统的设计方案
GPS驯服二级频标中的可驯服二级频标模块主要是由可压控的恒温晶体振荡器(VCOCXO)等组成。系统的总体设计方案如图1所示:
在图1中,所有在FPGA内部实现的数字逻辑部分均由一片FPGA来完成;而时间间隔测量模块中的数字逻辑部分由上述FPGA和一片CPLD互相配合来完成。图中的VCOCXO的输出频率一般选择为10MHz或者5MHz。
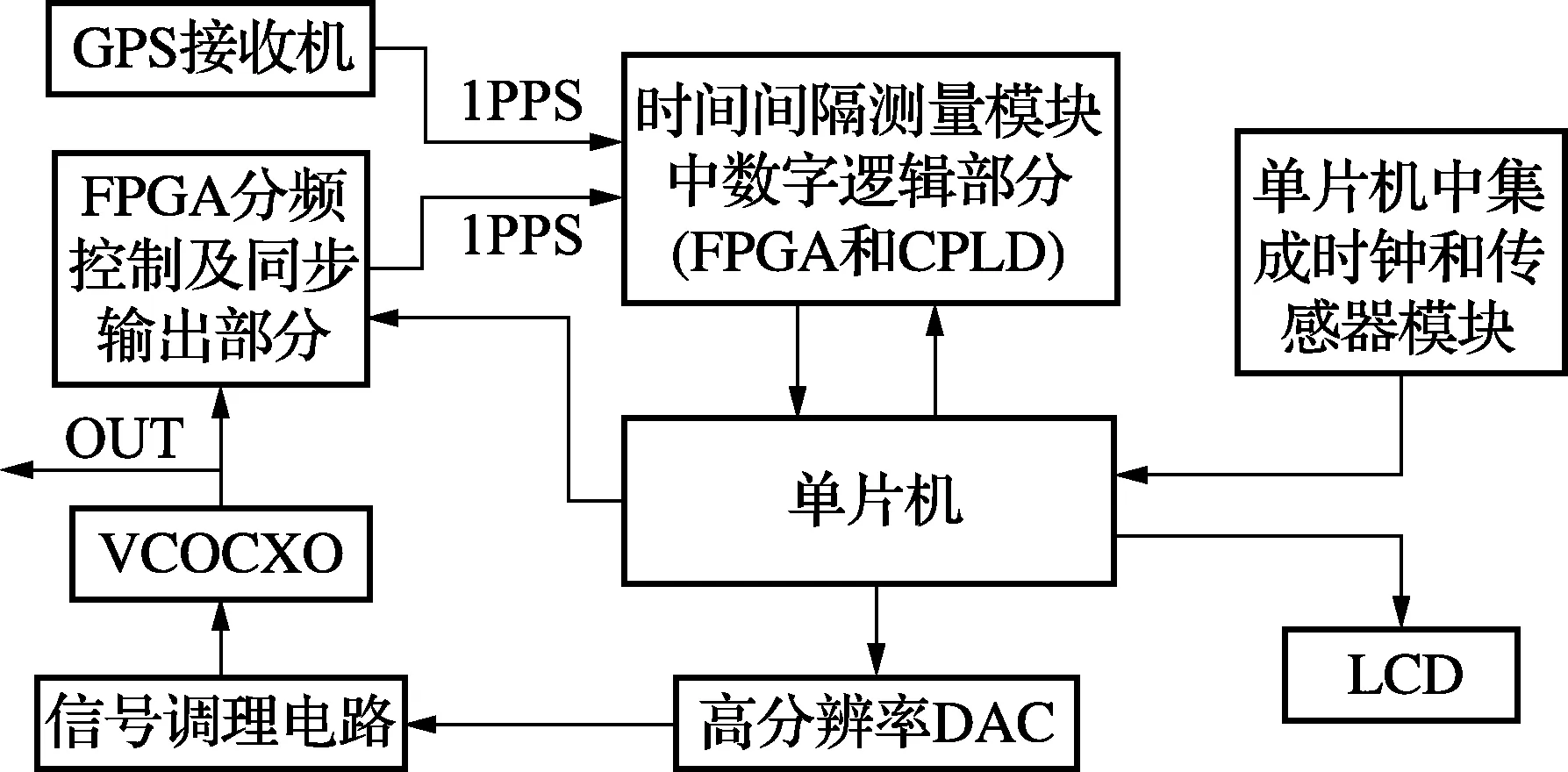
图1 系统的总体设计方案
1.1 GPS接收模块设计
GPS接收电路选择的新型LassenIQ型GPS模块,在接收信号微弱的时候,模块自动选择到高灵敏度模式。GPS接收机输出的1PPS信号中含有毛刺,需要采取抗干扰措施。这里采用了实时监测和开窗选通1PPS的方法[5]。在GPS信号接收模块中,当卫星数量少于4颗时,立刻屏蔽下传的1PPS;另一方面,通过开窗的方法实时监视相邻两个秒脉冲之间间隔的均匀性,发现异常立刻屏蔽1PPS[6]。初始触发分频信号到来后,计数器先是被复位,后开始计数,在计数值达到相应值时,输出同步“窗口”信号,只有处于“窗口”内的1PPS信号才可以通过。
1.2 时间间隔测量模块
采用了将直接计数法和时间-幅度转换法相结合的时间间隔测量方法,以此来实现两个1PPS信号之间的相位比对[7]。用可编程逻辑门阵列CPLD和片上集成有A/D转换器的单片机以及其外围的电流源电路、高速开关、小电容、放电MOS开关和时间-幅度的模拟转换结果在进入A/D之前所必需的信号调理电路来构建这部分测量模块。使用前需要对设计的时间间隔测量模块进行校准,而后将校准数据存入单片机自带的Flash存储器,测量时查表并线性拟合得到结果,这样减小了非线性误差。在原测量信号上附加了一级固定延迟使逻辑器件的反应速度引起的测量死区接近于零。还采用了两套充放电电路,彻底消除直接计数时存在的±1个字的跳变,其中一个的充电开始时间滞后另一个,其固定延迟选择为计数时钟周期的一半。
在实测频率fx和标称频率f0比较接近情况下,对该时间间隔测量模块的测量误差进行了测试,结果表明,该模块的测量分辨力为100ps。如果希望晶振能被校准到1×10-11,填充时钟频率为100MHz,测量Δt1和Δt2引起的最大量化误差都为±10ns,于是Δt1-Δt2引起的量化误差为±20ns,Δt1和Δt2为比时法测量频率相对准确度时,相邻两次相位比对测得的时间间隔值。假设晶振能被校准到5×10-12,则相对频率准确度偏差比它小一个数量级,即A为5×10-13。则比时法[6]中相邻两次时差测量之间的采样时间T可由公式:
(1)
算出为4000s,提高了频率校准的实时性,降低了老化对于校准过程的影响。
1.3 基于Kalman滤波的PID控制器
基于Kalman滤波的PID控制原理框图如图2所示:
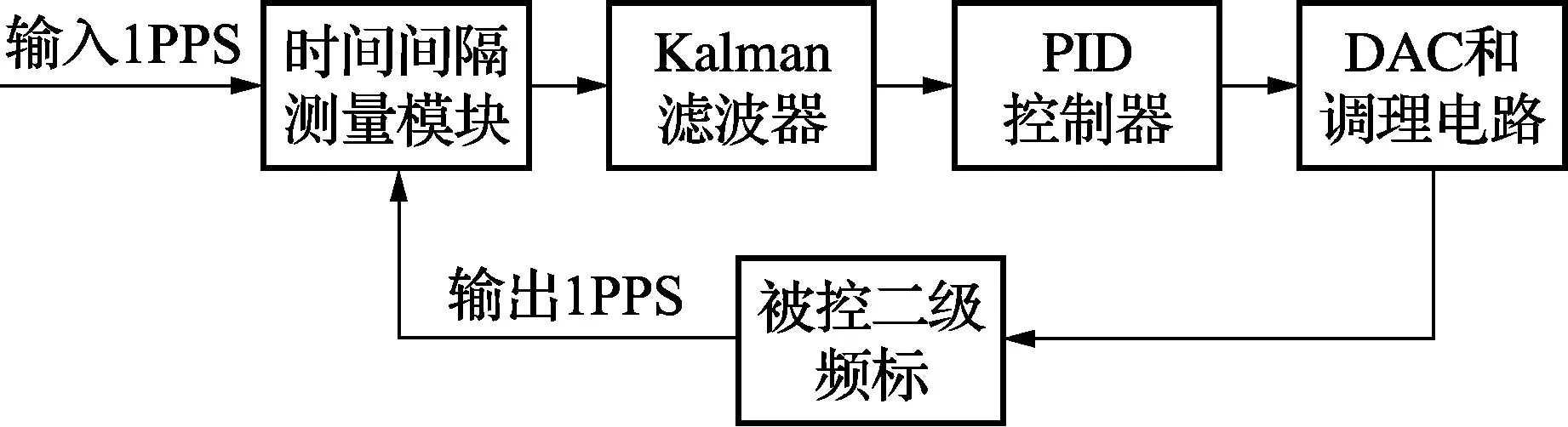
图2 基于Kalman滤波的PID控制原理框图
图3和图4是在初始相对频差约为+2.5×10-9并且驯服系统闭环后采集到的时间间隔测量模块直接输出和Kalman滤波后的相位差数据(采样周期为10s)。Kalman滤波可以较好地滤除强噪声背景下的噪声影响,而PID控制器可以很好地跟踪输入信号的相位,直至锁定。采用了Kalman滤波器后的PID控制更加平稳,“振铃”现象不明显。可以在较短的时间内达到稳态,即相对频差趋于零。
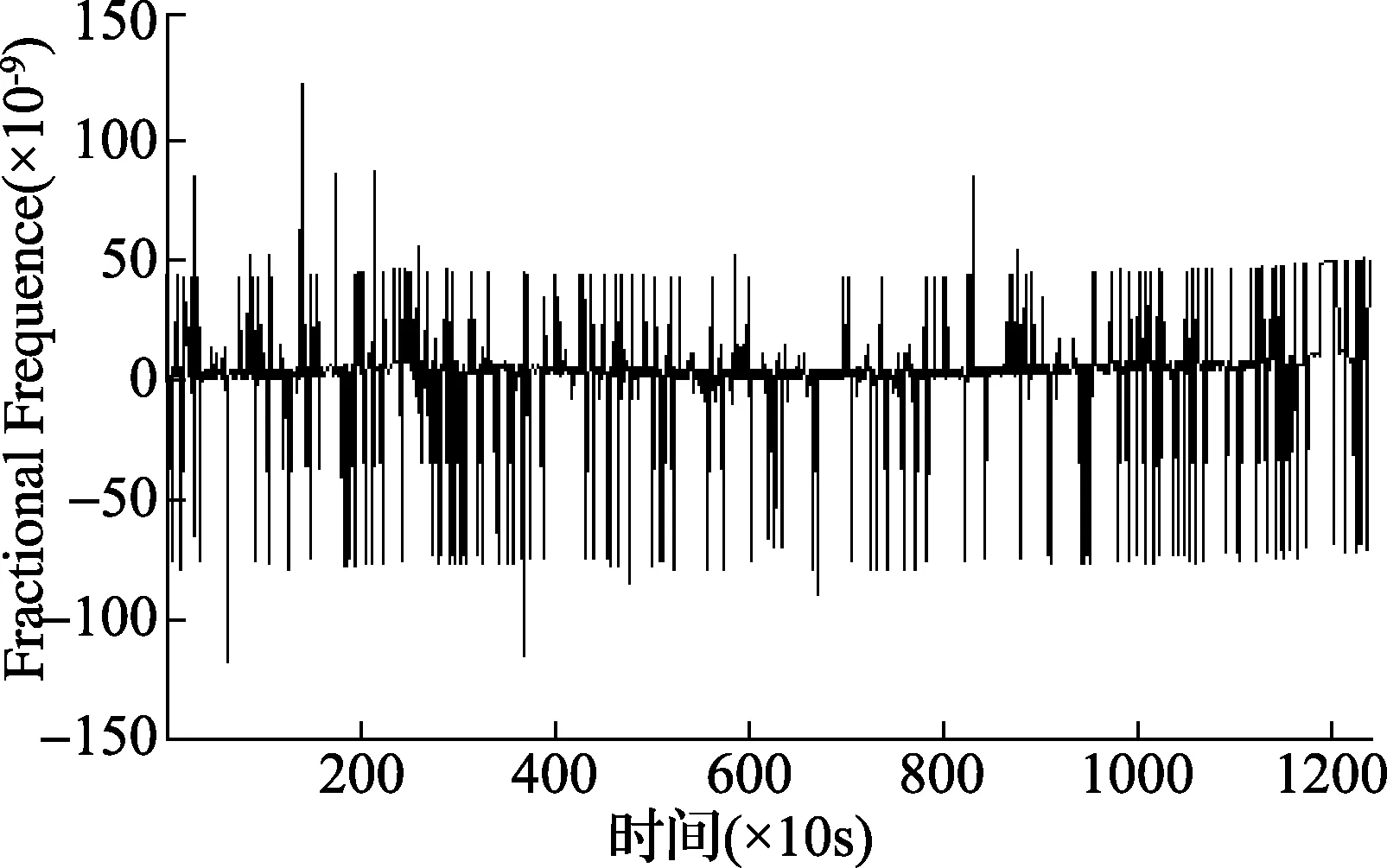
图3 PID控制器的滤波前波形图
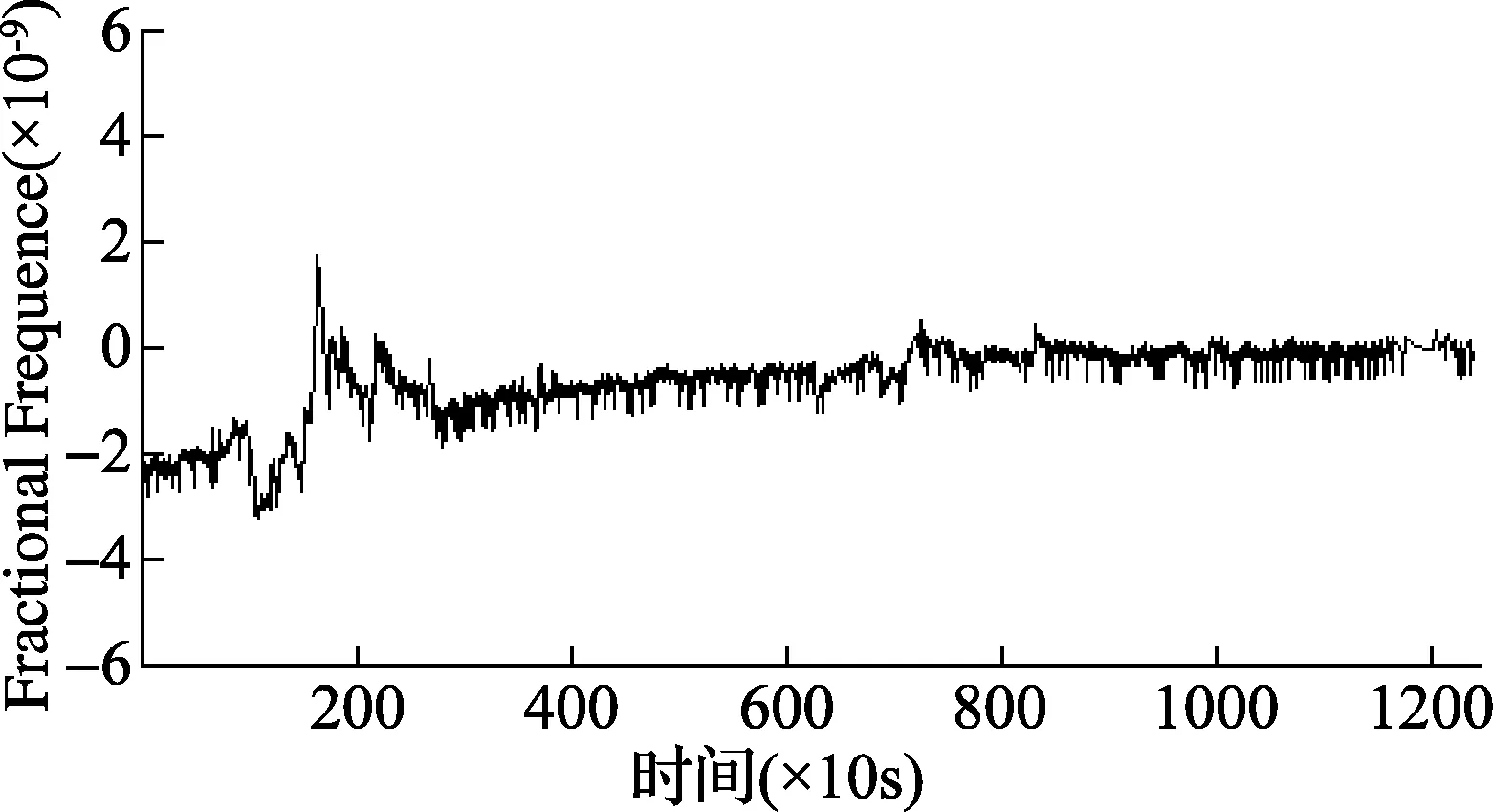
图4 基于Kalman滤波的PID控制器的滤波后波形
1.4 数字PID控制算法和失效保持算法
1.4.1 数字PID及其算法
离散的PID表达式[6]计算复杂,遂将其改进如下式:
(2)
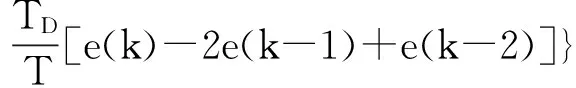
(3)
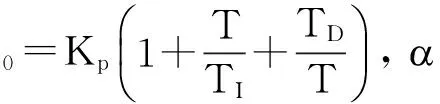
u(k)=u(k-1)+a0e(k)-a1e(k-1)+
a2e(k-2)
(4)
式(4)为PID的递推公式。PID算法对输入信号跟踪能力强,经过一段时间,可以使输入和输出信号的稳态误差趋于零。
1.4.2 老化率和温度预测模型
老化的预测模型采用矢量滤波器,即
信号模型:x(k)=ax(k-1)+ω(k-1)
(5)
观测模型:y(k)=cx(k)+v(k)
(6)
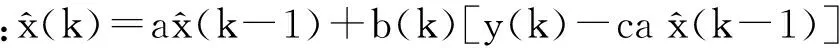
(7)
时变增益:b(k)=P1(k)cT[cP1(k)cT+R]-1
(8)
最小均方误差:Pe(k)=P1(k)-b(k)cP1(k)
(9)
其中:P1(k)=aPe(k-1)aT+Q
(10)
在老化的预测模型中,信号的状态向量是一个三维列向量[7-8]
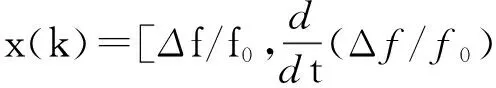
(11)
状态转移矩阵a取值[7-8]为:
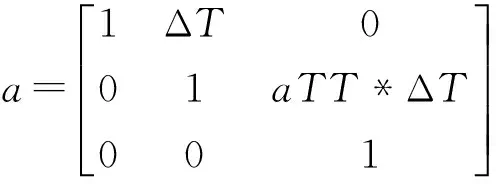
(12)
其中,Δt为采样周期,系数aTT在保持期间取值为0,以跟随老化率长期的非线性,防止错误更新。
测量参数矩阵c取值为:
c=[1,0,0]
(13)
Q为三阶方阵,所有数值设定在1×10-4量级;矩阵R值取为1.0。
温度影响预测也采用Kalman预测模型。温度预测模型中的状态向量[7-8]取为:
(14)
式中后面两项分别代表相对频差Δf/f0对温度T的一阶微分和二阶微分。
状态转移矩阵与式(12)相同,其中ΔT为温度随时间变化的斜率。这里用温度传感器输出数据的200点滑动平均来计算温度变化的斜率,从而消除了温度传感器的测量分辨率不够高及逐秒测量产生毛刺对预测的影响。矩阵中的系数aTT在正常驯服状态时取值为1,而在保持期间取值为0。
上述保持模型中所涉及到的算法均在单片机中实现,单片机会接收GPS信息,解码得到所跟踪卫星状态信息,当卫星处于不健康状态时,屏蔽接收到的1PPS信号,当确认卫星信号已彻底丢失时,训练还未完成,预测值会是最近100个驯服输出的滑动平均值;如果训练已完成,则预测输出是保持模型的输出。当卫星信号恢复正常,重新启动驯服程序,初始化保持模型,重新开始训练,如此循环往复,使得晶体振荡器输出频率的稳定度在锁定状态下达到4.3×10-13,保持状态下达到3.8×10-11。
2 实验结果及分析
基于GPS的二级频标驯服、保持系统样机、驯服系统的硬件和软件算法已完成,在此软硬件基础上,进行了一系列实验,以测试系统的驯服、保持能力。
采用比相法[5],将铯原子频标输出的10MHz和已驯服频标的输出进行相位比对,得到已驯服频标的频率准确度4.3×10-13。
对系统的保持性能进行了测试,测试时,在GPS信号正常且VCOCXO被锁定一段时间以后,拔掉了GPS天线,而后经过判断,系统自己进入保持模式。
上述保持期间的频率平均准确度为2.1×10-11,累积误差为6.456ns,这对于VCOCXO随着本身老化和环境温度变化所产生的频率漂移(老化率:5×10-10/日,频率温度系数:6~8×10-9/40℃)有一定的改善。
由于受到测频仪器测量分辨力的限制,在进行频率稳定度测试时,1s和10s的稳定度由直接测频法计算得到,而100s、1000s、5000s和10000s的由比相间接测频法计算得到。锁定后,VCOCXO的短期频率稳定度测试结果如表1所示,长期频率稳定度如表2所示。
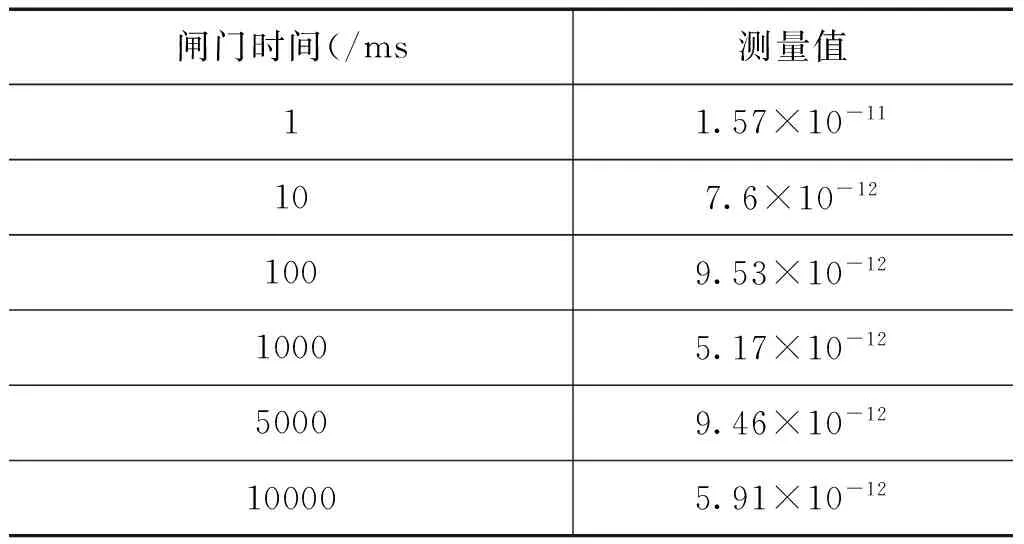
表1 VCOCXO的短期频率稳定度测试结果
从表2中可以看出,频率准确度在锁定状态下可达4.3×10-13,保持状态下可以达到3.8×10-11。
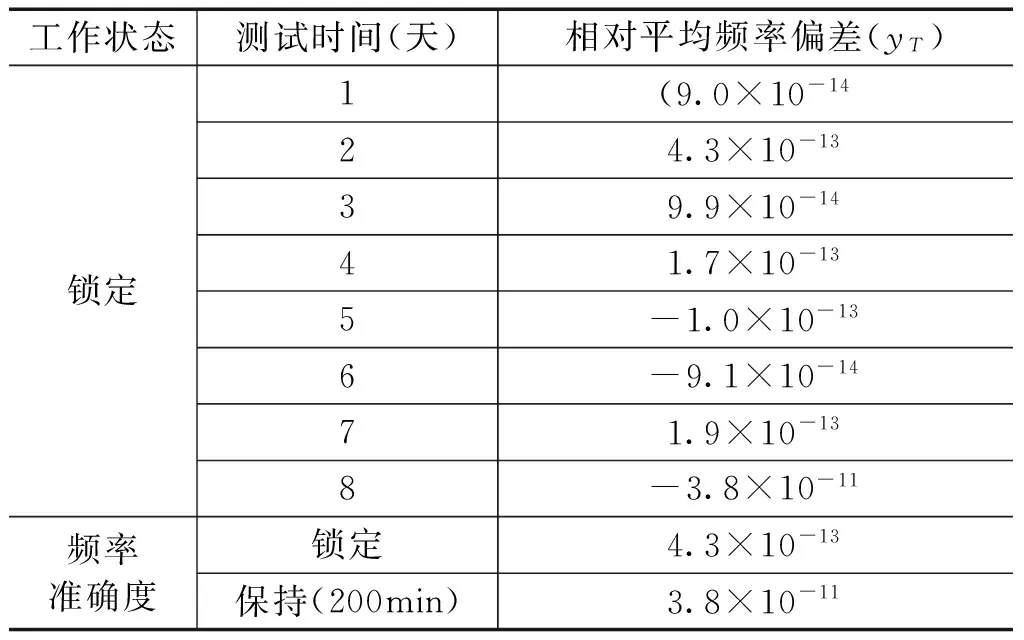
表2 VCOCXO的长期频率稳定度测试结果
3 结论
提出了一种基于GPS的1PPS信号的二级频标的驯服、保持系统。采用了将时间-幅度转换法和直接计数法相结合的时间间隔测量方法,对GPS接收机输出的1PPS信号与本地VCOCXO分频得到的秒信号进行相位差测量。在VCOCXO被锁定后,对驯服系统的性能进行了测试,测试结果表明锁定后该系统能输出高精度的频率信号,其短期稳定度总体优于其原有水平,秒级稳定度接近5.17×10-12/s,长期稳定度有所改善,天稳达到-9.00×10-14/天,解决了VCOCXO由于老化和温度所导致的频率漂移和长期稳定度差的问题,锁定后长期频率稳定度达到4.3×10-13,保持状态下长期频率稳定度指标达到3.8×10-11。
[1] 张鹏.基于GPS的电力系统同步时间服务系统的研究与实现.武汉:华中科技大学硕士论文.2005
[2] 易雄书.基于GPS的DMB-TH单频网时间同步系统研究.四川:西南交通大学硕士论文,2008
[3] Chia-Lung Cheng, Fan-Ren Chang, Kun-yuan Tu.Highly Accurate Real-Time GPS Carrier Phase-Disciplined Oscillator.IEEE Trans on Instrumentation and Measurement.Apr.2005.Vol.54,No.2.819-824.
[4] 郭向阳,赵振杰.自适应驯服铷钟的实现.飞行器测控学报,2006,25(4)
[5] 周渭,偶晓娟,周晖,等.时频测控技术(第一版).西安:西安电子科技大学出版社,2006
[6] 王光鼎,张升康,杨汝良.一种基于卡尔曼滤波处理的北斗卫星无源组合导航自适应野值剔除方法.电子与信息学报,2008,30(8)
[7] 孙江涛.恒温晶振OCXO自适应驯服保持技术研究.西安:西安电子科技大学硕士论文,2011
[8] C.W.T.Nicholls, G.C.Carleton.Adaptive OCXO Drift Correction Algorithm.2004 IEEE International UFFC Joint 50th Anniversary Conference.509-51
中央高校基本科研业务费资助(K5051304022)
10.3969/j.issn.1000-0771.2015.1.04

