激光跟踪仪测角精度评定方法
杨 凡 唐劲松 李广云 王 力
(1.信息工程大学测绘学院,郑州 450052;2.解放军73603部队,南京 210049)
激光跟踪仪测角精度评定方法
杨 凡1唐劲松2李广云1王 力1
(1.信息工程大学测绘学院,郑州 450052;2.解放军73603部队,南京 210049)
本文以Leica AT901_B激光跟踪仪为测试仪器,进行测角精度的评定研究。由于缺乏严密的角度检校标准,本文参考经纬仪/全站仪系统检校规范,提出以常规的角度检校模型为基础,采用全圆方向观测法获取数据,通过坐标反算观测值来计算系统轴系误差2C值和I角误差,并通过最小二乘平差原理解算系统水平角误差和垂直角误差。该方法基于严密的经纬仪/全站仪角度检校模型,真实地反映了激光跟踪仪的轴系误差和测角精度。通过数据的平差解算,求得AT901_B的水平和垂直测角精度分别为0.54″和0.52″,由此评定出AT901_B激光跟踪仪的实测精度符合其标称精度。
精度评定;误差模型;实测精度;标称精度;AT901_B
0 引言
激光跟踪仪是目前精度最高的便携式单点坐标测量系统,较之与经纬仪、全站仪、iGPS等系统,以其兼备精度高、范围大、速度快、操作简便和应用性强等优势,广泛应用于各计量部门和生产制造部门。该系统集成了动态编码测角技术、激光干涉测距技术、光电检测技术、计算机控制技术和现代数值理论等,实现了对空间目标快速跟踪并实时获取高精度三维坐标。该系统主要结构包括测角部分(水平度盘、垂直度盘)、测距部分(IFM、ADM)、激光发射器、控制器、反射器、步进马达、支架及外壳等。激光通过光路发射到目标,系统同时获取目标的角度和距离观测值,并采用极坐标原理计算得到三维坐标;当目标移动时,位置偏移量快速反馈到PSD(位置探测器),控制信号传递给马达并将激光束调整到新的位置,从而保证目标的实时跟踪。
激光跟踪仪的精度指标是厂家给定的,其与实测精度是否一致尚待验证。另外,仪器在长时间的使用后因搬运、磨损和放置等都会导致精度损失,为了保证测量数据的可靠性,定期的精度测试就显得十分必要。目前,针对激光跟踪测量系统检校的国内外规范主要有ASME B89.4.19—2006、JJF 1242—2010、GJB/J 6201—2008,它们都没有单独对测角精度进行系统测试。国内一些学者对此也开展了相关研究,如文献【1】提出了基距测量、双面测量和球形杆测量等方法反映系统的综合精度;文献[2]评定了Faro Xi的坐标测量精度;文献[3]分析了温度、反射器误差等对系统精度的影响;文献[4]研究了跟踪转镜结构的精度;文献[5]的飞机颤震飞行实验反映了系统误差对实测精度的影响,这些研究工作都没有针对测角精度进行深入探讨。基于以上现状,本文对激光跟踪仪的测角精度检定方法进行系统研究,并通过Leica A T901_B进行实验验证。
1 激光跟踪仪测角精度检定方法
由于激光跟踪仪的测角原理是光栅增量式动态编码原理,测角结构主要包括水平度盘和垂直度盘。为了分离水平角误差和垂直角误差,需要分别进行水平角精度测试和垂直角精度测试。
测角精度评定的基本思想是:在稳定的实验室环境,分别建立水平角和垂直角检校场,场内目标点分布必须覆盖仪器的整体角度测量范围,以全圆方向法分别获取水平面和垂直面观测值,在多测回多观测量的基础上通过最小二乘平差原理计算水平角精度和垂直角精度,以及系统轴系误差2C值和I角误差。
1.1 水平角精度测试方案
如图1所示,在仪器周围均匀布设若干目标点,按顺序命名为1,2,…,n,覆盖仪器的水平角测量范围(通常是360°),目标点与仪器同高,保证测角误差不包含垂直角误差。采用全圆方向盘左盘右的观测方法,盘左观测从目标点1开始,依次测量2,3,…,n,1,回到零方向位置1后仪器翻面,开始盘右观测,顺序是1,n,9,…,2,1,完成一测回观测。为了反映仪器的真实测角精度,必须保证足够的观测值,因此需要进行多测回观测。直接输出值是目标点坐标,通过公式a =arctan(y/x)反算水平角,利用双面观测值取中数得到一测回方向值Mij=(aL+aR±180°)/2,式中,i表示测回序号;j表示目标点序号。
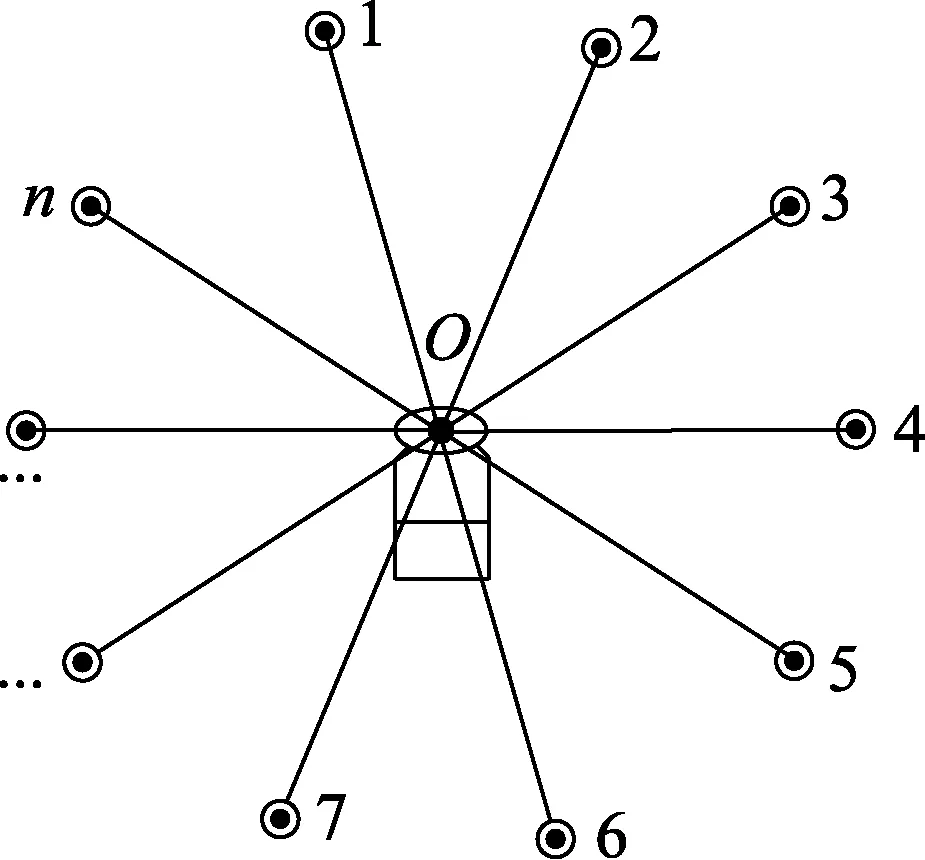
图1 水平角检校场
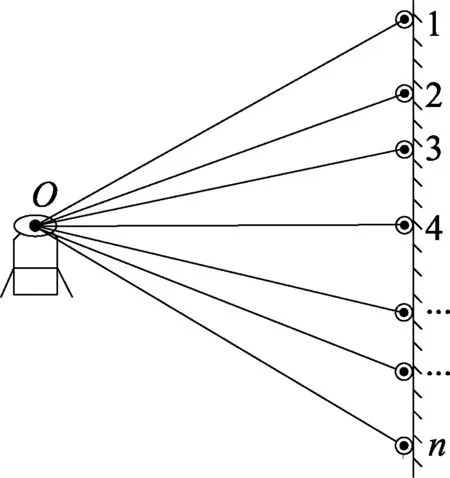
图2 垂直角检校场
1.2 垂直角精度测试方案

1.3 测角精度检定模型
在获得角度观测值后,首先做数据预处理,剔除粗差,利用重复观测数据检查数据可靠性;然后建立水平和垂直角误差模型,通过最小二乘平差解算实测精度,将其与标称精度对比、分析,评定激光跟踪仪的测角精度。
(1)


(2)
式中,n为目标点数。
激光跟踪仪在应用中通常只进行单面观测来获取单面观测数据,为了反映单面观测值的精度情况,此处同样可利用式(1)和式(2)计算单面观测值的测回中误差。
2 Leica AT901_B测角精度检定
本文以Leica AT901_B激光跟踪仪为例进行测角精度的检定,反射器采用CCR1.5″的角隅球形棱镜,系统主要精度指标如表1所示。
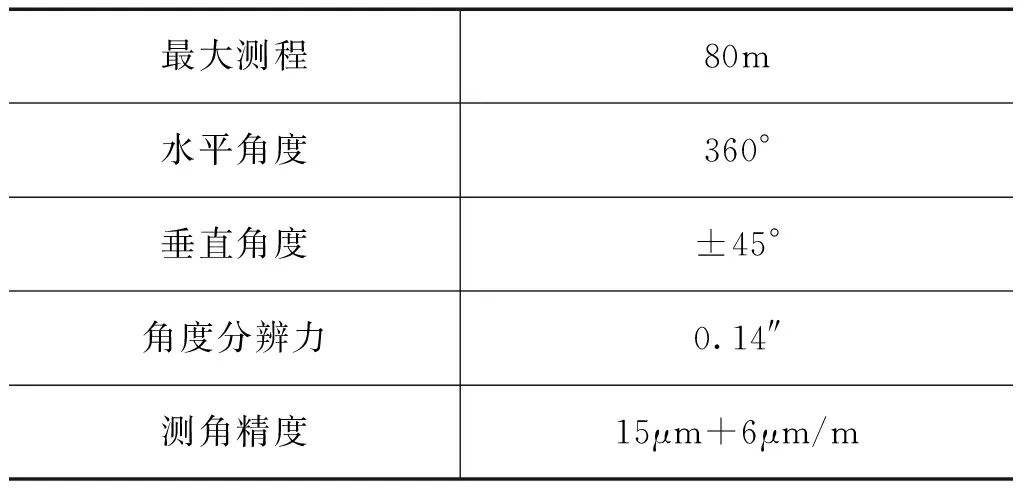
表1 AT901_B标称精度
根据现有的实验环境,将检校场作了如下布置:水平角检校场均匀布设10个角隅棱镜靶座,各靶座和仪器的距离不同,呈远近分布,高度与仪器一致,覆盖仪器360°的水平角测量范围,在同一测站进行5个测回的数据采集;垂直角检校场在不同高度均匀布设7个角隅棱镜靶座,覆盖仪器±45°的垂直角测量范围,在仪器测程内从远到近共5次设站,设站1~5离目标点的近似距离依次为48m、38m、28m、18m和10m,每测站进行6个测回的数据采集;为了考虑整平对测量结果的影响,采用LeicaNivel230水平仪(精度为±1.1″),在该实验中分别进行了仪器整平和不整平两种情况的数据采集。
2.1 二倍视准差2C和垂直度盘指标差I
二倍视准差2C和垂直度盘指标差I可以反映仪器的系统误差及数据的可靠性,计算公式如下
2C=aL-aR±180°
(3)
(4)


表2 二倍视准差2C
从表2可以得出如下结论:
1)AT901_B的2C均值为2.7″,I均值为1.6″,两者波动范围均不大,反映了仪器良好稳定的工作状态。
2)仪器整平与否对2C和I的影响不大。
3)如果去掉差值最大的测回观测值,2C值精度可以提高0.2″~0.4″。
2.2 水平角精度
将测量得到的10个目标点P1,P2,…,P10,各5个测回数据按照测角精度模型处理后,得到水平角一测回方向中误差以及单面观测中误差,如表3所示。
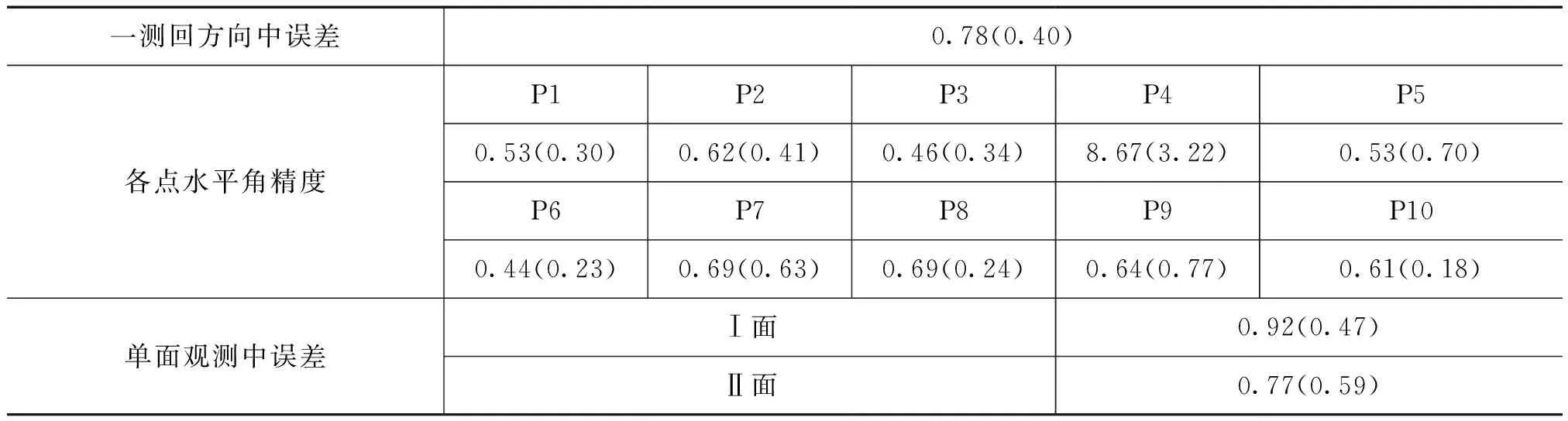
表3 水平角检定误差 未整平(整平)(″)
从表3可以得出如下结论:
1)各点水平角精度相当,与目标点距离没有必然联系。
2)仪器整平对水平角的测量精度有一定程度的改善。
3)10个目标点分布在距仪器3.6~6.9m的范围内,标称精度15μm+6μm/m,换算到该范围的标称角度精度为1.7″~2.1″,数据显示实测精度满足标称精度。
4)P4点的精度较差,检查原始数据后分析认为由于测量过程中靶座的松动导致。
2.3 垂直角精度
同理,将垂直角检校场测量得到的7个目标点各6个测回数据按照测角精度模型处理后,得到垂直角一测回方向中误差以及单面观测中误差。将标称精度15μm+6μm/m换算成相应距离的角度精度指标与实测精度进行对比,结果如表4所示。
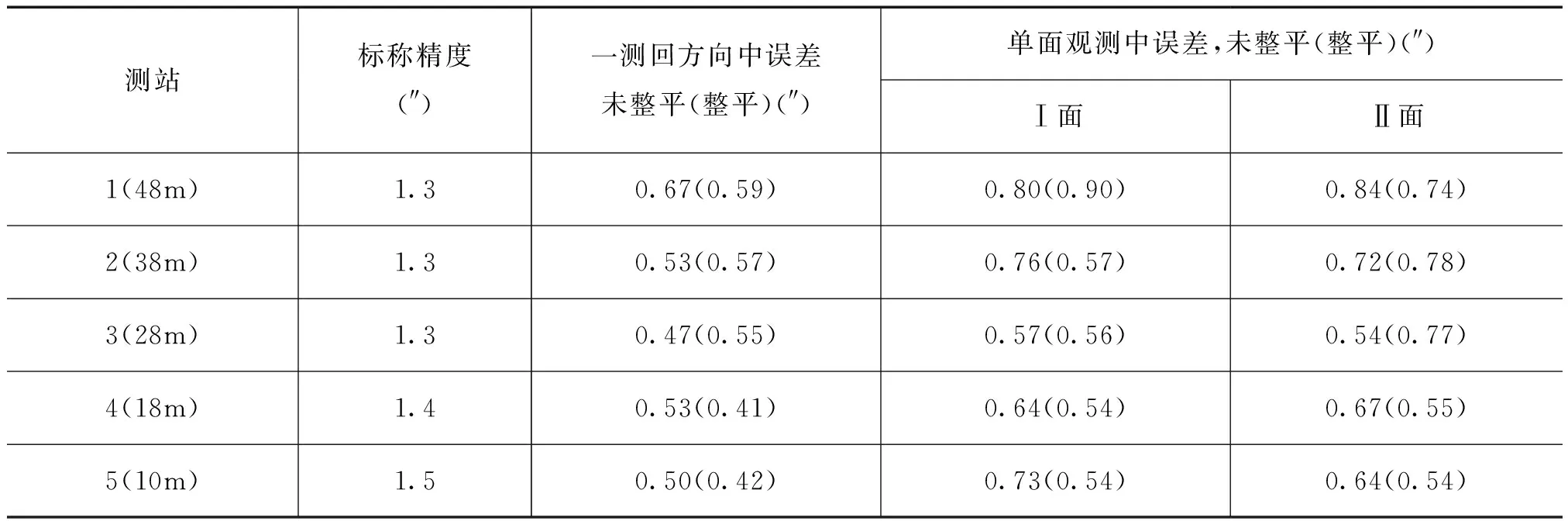
表4 垂直角检定误差
从表4可以得出如下结论:
1)垂直角双面观测值精度均值为0.52″,单面观测值精度分别为0.67″和0.68″,都满足标称精度,双面观测值精度略好。
2)Ⅰ面和Ⅱ面的垂直角观测精度没有明显差异。
3)仪器整平与否对垂直角双面观测精度和单面观测精度没有明显的影响。
4)垂直角双面和单面观测值精度和测站与目标点之间的距离没有比例关系。
3 结束语
本文对激光跟踪仪的水平和垂直测角精度检定方法进行探讨,基于经纬仪/全站仪测角精度检定方法提出了适合于激光跟踪仪的测角精度检定模型,并以Leica AT901_B为例进行了实验验证。通过实验可以看出,Leica AT901_B的水平角一测回方向中误差为0.54″,垂直角一测回方向中误差为0.52″,由此可评定出Leica AT901_B激光跟踪仪的实际测量精度符合其标称精度,跟踪仪处于正常的工作状态。该实验还深入研究了激光跟踪仪2C误差、I角误差以及双面观测值、单面观测值、Nivel230整平等因素与测角精度的联系,得出了诸多有效结论,比较系统地总结了激光跟踪仪测角精度的检定方法。
[1] 李广云.LTD500激光跟踪测量系统原理及应用[J].测绘工程,2001,10(4):3-8
[2] 欧阳健飞.激光跟踪仪坐标测量精度的研究[J].红外与激光工程增刊,200(37):15-18
[3] 赵树忠.提高激光跟踪三维坐标测量精度的研究[D].天津大学,2007
[4] 李杏华.跟踪机构精度检测的研究[J].计量技术,200(5):7-9
[5] 王彦.激光跟踪仪测量系统校准技术研究[J].测试技术,2003(3):37-41
[6] JJG 100—94《全站型电子速测仪》,1994
[7] 陈继华.激光跟踪仪和全站仪测量系统在上海光源(SSRF)工程中的应用研究[D].中国人民解放军信息工程大学测绘学院,2001
[8] JJF 1242—2010《激光跟踪三维坐标测量系统校准规范》,2010
[9] B.Muralikrishnan, D.Sawyer, C.Blackburn, S.Phillips, B.Borchardt, and W.T.Estler.《Performance Evaluation of Laser Tracker-Based Spherical Coordinate Measurement Systems ASME B89.4.19—2006》, Journal of Research of the National Institute of Standards and Technology, 2009
[10] 马骊群, 王继虎,等.激光跟踪仪测角误差的位移标定法[J].计量学报, 2009, 30(5A): 76-79
10.3969/j.issn.1000-0771.2015.1.07

