差动式电容传感器数字解调技术*

黄利红 郭唐永 邹 彤 吴 涛

(1.中国地震局地震研究所(地震大地测量重点实验室)，武汉 430071；2.中国地震局地壳应力研究所武汉科技创新基地，武汉 430071)



差动式电容传感器数字解调技术*

黄利红1,2郭唐永1,2邹 彤1,2吴 涛1,2

(1.中国地震局地震研究所(地震大地测量重点实验室)，武汉 430071；2.中国地震局地壳应力研究所武汉科技创新基地，武汉 430071)

在大地测量中，我们对如何检测出地壳微小的变化很感兴趣，利用差动式电容传感器可以检测出这种微弱的信号。本文对差动式电容传感器的输出信号进行数字化解调，介绍了三种解调方法，分别是数字包络解调、数字正交相干解调及基于Goertzel算法的解调。文中给出了各自的原理，并用Matlab对给出的信号进行了仿真比较，结果分析。

差动式电容传感器；数字解调；数字包络解调；数字正交相干解调；基于Goertzel算法的解调

0 引言

地壳倾斜的变化极其微小，要对其进行观测，必须有能测量出微小位移的器件，一种方法是将这种微小的变化放大后再测量，另一种方法是通过电容测微传感器检测，如利用差动式电容传感器。差动电容传感器的输出电压很小，易被噪声淹没，因而，必须经过高增益放大才能检测出所需信号。经高增益放大后，还需要经过锁相放大器滤波。

锁相放大器抗噪声性能非常好,将交流信号放大且变成相应的直流信号,即检测出并放大相应的同步信号。这种模拟解调的方法能满足仪器的各项指标，但数字信号相比于模拟信号有易于存储，便于处理及可靠性高等优点。考虑将数字技术应用到仪器上面，相对于模拟电路，能提高仪器的可靠性，减少调试工作量。而仪器的数字化改造首先要将模拟解调数字化，即数字化解调方法的实现。

1 数字化解调方法

从差动式电容传感器的检测原理知，可将已调制信号设为

y[n]=Ax[n]cos(w0n+θ)

(1)

1.1 数字包络解调

调制信号的信息包含在载波的包络中，而载波的各个幅值点组成了载波的信号包络。通过某种算法来得到幅值点以获得信号包络从而实现解调。

由式(1)知

在一个载波周期内有fs/f0个采样点，将每个载波周期中的最大幅值点取出，并在周期末输出。当载波频率非常大以及采样频率过高时，可多个载波周期输出一个幅值。数字包络解调流程图如图1所示。在图1中，描述的是某个载波周期处理的过程，第1步先输入初始值到存储大的幅值中储存；第2步将输入的值放入比较中；第3步将存储大的幅值与比较的值进行比较，将大的赋值给存储大的幅值，重复2、3、4步，一直到得到这个载波周期的最大值，最后一步是第5步，将这个最大的值给输出。

新载波周期图1 数字包络解调流程图

1.2 数字正交解调

数字正交解调框图如图2所示。

图2 数字正交解调框图

ri[n] =y[n]cos(w0n)

=Ax[n]cos(w0n+θ)cos(w0n)

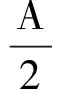
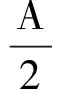
rq[n] =y[n]sin(w0n)

=Ax[n]cos(w0n+θ)sin(w0n)

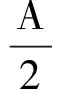
经低通滤波器滤波后

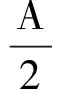
1.3 基于Goertzel算法解调

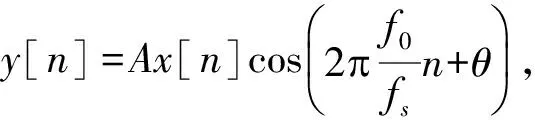
m[n] =y[n]w[n]

做傅里叶变换得

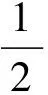
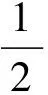
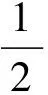
因而，在解调过程中仅需求载波频率处的DFT。

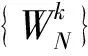
期望输出X(k)=yk(n)n=N，其中k=0,1，2，…，N-1。

式中，WN=e-j2p /N

相应的系统函数为

(2)

为了避免式(2)所蕴含的复数乘法和加法，可以合并拥有复共轭极点的谐振器对。这时，系统函数变为

(3)

差分方程描述为

(4)

(5)

2cos(2pk/N)vk(N)vk(N-1)

(6)

初始条件为vk(-1)=vk(-2)=0。

2 对比分析

设差动式电容传感器载波频率为100kHz，在Matlab仿真中，选取调制信号频率f为0～20Hz，载波频率f0=100kHz的信号进行解调，采样频率fs=800kHz，分别加入信噪比SNR为0～30dB的高斯白噪声。选取f=5Hz，SNR=10dB的仿真图进行比较，其中包络解调以10个载波周期输出一个幅值。程序是在Matlab2010上运行的，选取的是8个调制信号周期长度的数据量。

图3(a)是待解调信号的波形图及频谱图。图3(b)(c)(d)中的子图a1、a2、a3分别是用三种方法解调出的信号的波形图，可以看出，它们都成功实现了解调的功能；子图b1、b2、b3是加入噪声的波形图；子图c1、c2、c3是有噪声解调出的信号与无噪声解调出的信号之差。子图c1中信号的大小几乎是子图b1中信号大小的1/4，子图c2中信号的大小也几乎是子图b2中信号大小的1/4，子图c3中信号的大小与子图b3几乎一样。因此，在抗干扰方面，基于Goertzel算法的解调与正交解调都有一定的抗干扰能力，包络解调则没有。

图3 解调效果图

基于Goertzel算法的解调，由式(3)它的系统函数中可以看出，它的分母部分是一个二阶系统，相当于一个线性的二阶滤波器，因而有一定的滤波功能。从图2正交解调框图中，可以看到，在正交解调过程中，两路信号分别都需经过一个低通滤波器，因而解调出来的信号也有一定的滤波效果。在包络解调中，由于包络解调只是简单的将每个载波周期的最大值取出，因而无法对信号滤波，在信噪比低时，干扰严重，解调效果不好。

在基于Goertzel算法的解调中，由于它的系统函数式(3)合并了拥有复共轭极点的谐振对，因而在它的递归关系式(4)中，系数均为实数，将复数乘法简化成了实数乘法，节约了运算量。正交解调由于两路信号先要经过乘法器，再经过低通滤波器滤波，最后还要实现平方和再求根这个过程，实现过程较复杂，耗用资源。

从图3子图a1、a2、a3及图3(e)中，还可以看出，基于Goertzel算法的解调还有一定的放大功能，它将信号放大了4倍。

表1～表3列出了f=1、5、10、20Hz，SNR=1、5、10、15、20、25、30dB的条件下，三种方法输出的幅度最大点,其中包络解调以10个载波周期输出一个幅值的方式。程序是在Matlab2010上运行的，选取的是8个调制信号周期长度的数据量。

表1 包络解调输出幅值最大点

表2 正交解调输出幅值最大点

表3 基于Goertzel算法解调输出幅值最大点

从3个表格可以看出，在同频率的情况下，基于Goertzel算法解调输出值幅度最大点是正交解调输出幅度最大点的4倍，包络解调由于选取的是8个点取1个值，计算频谱值时点数是正交解调的1/8，因此，它的幅度最大点是正交解调的1/8。

3 结论

数字相干解调实现过程复杂，非常耗用资源；数字包络解调实现原理简单，但在信噪比低的情况下，解调性能非常差，抗干扰能力差而无法将被噪声淹没的信号取出，而基于Goretzel算法的解调抗干扰能力好，运算过程为实数运算因而运算速度较快并且易于实现。因此，在仪器的数字化改造中，与模拟解调对应的数字解调方法可以采用基于Goertzel算法解调进行尝试。

[1] Joyce Van de Vegte.数字信号处理基础[M].北京：电子工业出版社，2003

[2] SanjitK.Mitra.数字信号处理-基于计算机的方法(第四版)[M].北京：电子工业出版社，2012

[3] 李莹.静电反馈技术在倾斜仪中的应用研究[D].武汉：中国地震局地震研究所，2009

[4] 王庆河,王庆山.数据处理中的几种常用数字滤波算法[J].计量技术,2003(04):53-54

[5] 张肃文.高频电子线路(第四版)[M].北京：高等教育出版社，2004

[6] 梁志国.周期信号的谐波分析述评[J].计量技术,2003(02)

[7] 胡国新.新型倾斜仪机械结构研究及误差分析[D].武汉：中国地震局地震研究所，2012

[8] 陈怀琛.数字信号处理教程-MATLAB释义与实现(第3版)[M].北京：电子工业出版社，2013

[9] 胡广书.数字信号处理理论算法与实现(第三版)[M].北京：清华大学出版社，2012

[10] 江志红.深入浅出数字信号处理[M].北京：北京航空航天大学出版社，2012

湖北省科技支撑计划项目(2014BEC090)

10.3969/j.issn.1000-0771.2015.08.01