坐标转换在应用中的问题及解决方法

李明慈 黄桂平 李 冰 周克勤 张姝颖 林德欣

(1.北京建筑大学，北京 100044；2.华北水利水电大学，河南 450045；3.成都理工大学，四川 610059;4.天津市电子机电产品检测中心，天津 300074)



坐标转换在应用中的问题及解决方法

李明慈1黄桂平2李 冰3周克勤1张姝颖4林德欣4

(1.北京建筑大学，北京 100044；2.华北水利水电大学，河南 450045；3.成都理工大学，四川 610059;4.天津市电子机电产品检测中心，天津 300074)

随着坐标转换在测量中的广泛使用，针对不同的应用情况就可能面临不同的问题，本文对于坐标转换时面对的公共点匹配、简易且严密的转换参数算法等问题，提出了距离匹配和自由匹配解决公共点匹配的问题，简捷的精密参数解算法解决转换参数严密快速解的问题。最后通过数据进行实验，证明了精密计算转换参数方法的可行性。

坐标转换；罗德里格矩阵；公共点匹配；严密解

0 引言

空间直角坐标的转换在大地测量、工程测量、工业测量、摄影测量以及三维激光扫描测量等领域中[1-2]起着关键作用，特别是在工业测量中经常会进行测量坐标系与设计坐标系以及多个测量坐标系之间的转换，还有在摄影测量中空间后方交会、共线方程的建立以及在电子经纬仪交会测量系统中的软件数据处理中都要用到空间直角坐标系的转换[3-4]。

目前坐标转换的方法有很多，如非线性最小二乘法[5]、奇异值分解法(SVD)、四元数法和罗德里格矩阵法等，这些方法针对坐标转换时出现的大旋转角、迭代初始值选取等情况，从理论上很好地解决了这些问题，然而，在运用这些理论进行坐标转换的过程中还会面临另外一些更加现实的问题。比如，当两组坐标公共点之间的对应关系知之甚少或者完全不知道时，该如何自动地建立公共点的对应关系；如何快速获得两坐标系之间的精密转换参数？本文考虑到罗德里格矩阵法既可以解决大旋转角情况，又无需初始值的特点，选取此法作为坐标转换的计算方法，对转换过程中出现的问题加以阐述并提出相应的解决方法。

1 罗德里格矩阵方法的数学模型

(1)

此处的测量点和参考点视为同长度基准，即尺度因子默认为1。

式(1)中旋转矩阵可由罗德里格矩阵3个独立参数a,b,c表示[8]，设反对称矩阵S为：

(2)

则R可由S构成罗德里格矩阵表示：

R=(I-S)-1(I+S)

(3)

经计算旋转矩阵可表示为：

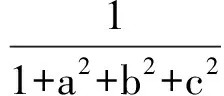
(4)

将式(3)代入式(1),得

(5)

设式中

(6)

(7)

将式(2)、(6)代入式(5)，变换得

(8)

根据式(8)可知，n个点对共有3n个方程，其矩阵形式如下

(9)

则式(9)可简写为

MD=L

(10)

由最小二乘法得

D=(MTM)-1(MTL)

(11)

将a,b,c代入式(4)，便可得旋转矩阵R，进而求得旋转角。将u,v,w代入式(7)可得平移参数T。由此求得转换参数。

2 实际面临问题

2.1 公共点匹配问题

在测量中尤其是在工业测量中经常会面对通过一系列公共点将测量的坐标转换到设计坐标系下。由于测量时公共点的编号和设计坐标系下公共点的编号方式不同，经常要手动对测量坐标系下的公共点进行重新编号或调整顺序，使两个坐标系下的公共点编号或公共点的排列顺序相同。若是存在大量公共点时这种手工操作不仅会影响工作效率，还可能出现错误。于是就面临如何准确、快速地完成公共点之间的匹配。

2.2 严密转换参数的简捷计算

使用罗德里格矩阵法只能获得坐标转换参数的初值，也就是说仅单次使用罗德里格矩阵方法计算精度不高。文献[9]中详细介绍了使用最小二乘的方法来计算转换参数的严密解，但是该方法复杂不易实现。如何才能较容易地实现转换参数的精密解也是现实中面临的一个问题。

3 解决方法

3.1 公共点匹配

解决公共点匹配的问题可以分为两种情况：已知部分公共点的对应关系和完全不知道公共点的对应关系。前一种问题的解决方法称之为距离匹配；后一种称之为自由匹配。

3.1.1 距离匹配

设测量点中Pi与参考点中的Qi(i=1,2,…)是一对公共点。

计算步骤如下：

1)利用已知的公共点信息(测量点和参考点中必须存在3对或3对以上的已知公共点)进行初始计算，获得初步的转换参数R0,T0；

2)使用初步转换参数将测量点Pi的坐标转换到参考坐标系下，设Pi转换后为Qpi；

3)利用Qpi的坐标与对应参考点Qi的坐标计算距离匹配时的阈值，公式如下：

(12)

4)利用R0,T0将所有的测量点转换到参考点坐标系中获得初步转换坐标；

5)利用第3步中获得匹配阈值hold，以参考点顺序为基准在第4步中获得的初步转换坐标中寻找与自己距离最小且小于阈值的点，若找到则记录下此时的参考点点名和测量点点名组成公共点对；

6)使用第5步中获得的点对进行坐标转换参数的计算，获得转换参数R，T。

以上过程我们称之为距离匹配。

3.1.2 自由匹配

根据刚体变换中，坐标转换前后的点间距不变的性质[10]，首先在参考点集中根据RANSAC算法[11]随机选取4个点记为q1,q2,q3,q4，并计算这4个点之间的距离S12，S13，S23，S14，S24，S34。根据距离S12，S13，S23在测量点中寻找与这三边距离相对应的点，记为p1，p2，p3，然后再根据S14，S24，S34寻找p4。若在测量点中找不到对应的点则重新在参考点中取点直到在测量点和参考点之间找到4个对应的公共点对。

在获得4个公共点对之后，其后的过程和距离匹配一样。我们把此种方法叫做自由匹配。

3.2 精密计算转换参数

由于基于罗德里格矩阵的最小二乘严密算法复杂不易实现，在此考虑将参考点在转换过程中固定，使测量点逐渐向参考点逼近，使测量点与参考点最佳贴合，最终达到精密转换的目的。

设测量点为Coord1，参考点为Coord2，转换一次后的测量点为Coord1(1)，转换k次后的测量点为Coord1(k)。Coord1和Coord2求得的旋转矩阵为R0，平移参数为T0，Coord1(k)和Coord2求得的旋转矩阵为Rk，平移参数为Tk。则：

Coord1(k+1)=Rk·Coord1(k)+Tk

(13)

得：

(14)

此时测量点Coord1(k+1)所在坐标系已经非常接近参考点Coord2所在坐标系，可把Coord1(k+1)所在坐标系看做参考坐标系。

由式(11)得平移参数计算较困难，因此可先计算旋转矩阵，再根据旋转矩阵求得平移参数，设

(15)

(16)

则：

T=Coord1(k+1)-R·Coord1

(17)

设定迭代次数k进行计算，最终求得测量点的转换坐标和转换参数。经过试验当迭代次数k>2时测量点转换后的精度便很难再有提高，而过多的迭代次数反而增加了运算量。

这种方法避免了最小二乘法中对观测值方程的线性化，极大地简化了计算过程。尤其是在通过编程实现时只需编写一个计算转换参数和计算转换坐标的函数，在进行精密计算时反复地调用这两个函数便可实现坐标转换的严密解，使计算简易的优越性更加突出。

4 计算示例与结果

这里主要验证精密计算转换参数的方法是否有效。取8组实测数据(如表1所示)代入计算。总体转换精度用点位偏差的均方根(RMS)来评定。设测量点转换得到Coord1′。

(18)

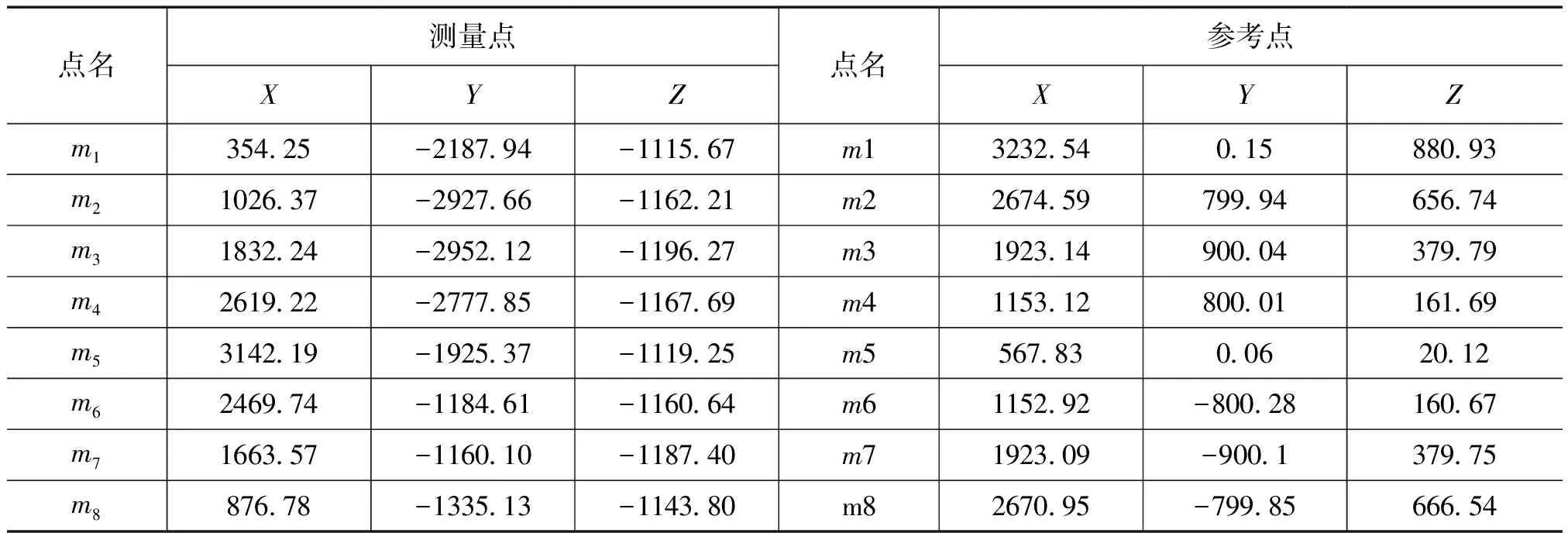
表1 实验数据 单位：mm

将测量点坐标分别使用罗德里格矩阵法和本文提出的精密简捷算法转换到参考点坐标系中，转换后的对应点位偏差如图1所示。

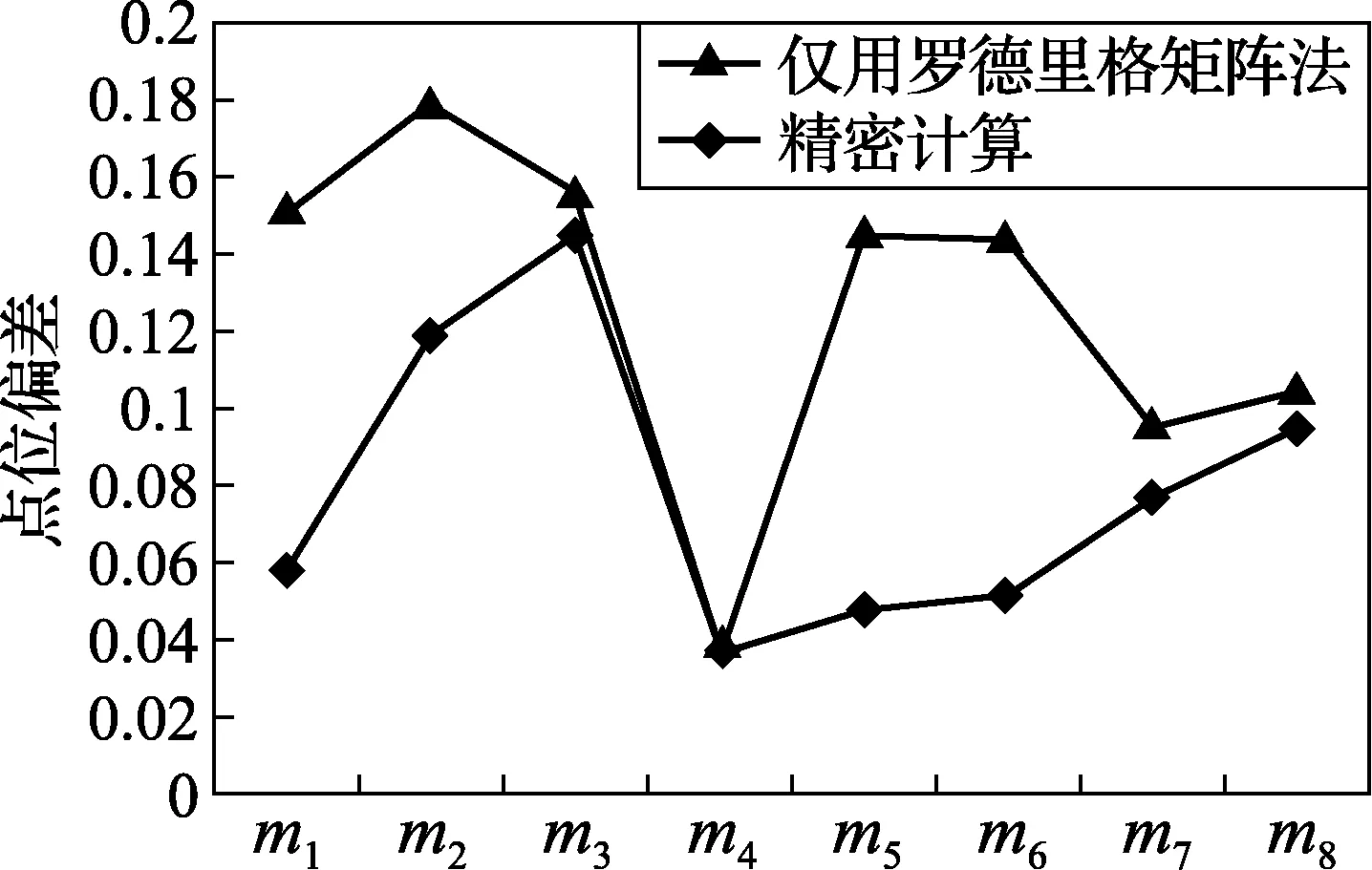
图1 罗德里格矩阵法和精密计算结果对比

从图1可以看出使用本文提出的精密简捷算法与仅用罗德里格矩阵法相比转换后的点位偏差明显偏小。运用公式(18)计算仅用罗德里格矩阵法转换后的点位偏差均方根为0.134，使用精密简捷算法转换后的点位偏差均方根为0.087，两者相对比精密简捷算法对最后测量点的转换精度有明显的提高。

下面验证精密计算的方法能否达到文献[9]中最小二乘严密计算的结果。实验采用文献[9]中表1的数据。采用本文中精密计算的方法，结果如表2所示。

表2 文献中数据精密计算结果 单位：m

由文献[9]中公式

(19)

计算转换总误差为0.0000441与文献[9]中表2给出的通过最小二乘严密解计算的总误差0.000045相比稍好。因此可得本文中的精密计算方法完全可以实现坐标转换的高精度严密解。

5 结束语

由于坐标转换在测量中使用的广泛性，使得如何在各种条件下准确、快速的求得转换结果成为一个无法回避的问题。本文以罗德里格矩阵法计算坐标转换参数为基础，阐述了坐标转换在实际计算过程中面临的公共点匹配、如何简捷地求得严密解等问题，并提出了各自相应的解决办法。其中距离匹配、自由匹配使得两个不同坐标系间能够自动且快速地完成公共点匹配，不仅减少了手动匹配错误的概率，而且提高了计算效率；转换参数的精密快速解在得到精密的坐标转换参数同时也对计算效率有所提高，而且与最小二乘严密解相比该算法还降低了程序实现的难度。最后对本文提出的精密计算转换参数方法的有效性进行了验证，并将其与基于罗德里格矩阵最小二乘严密解的方法进行对比，证明了本文提出的方法完全可以满足严密解的需要。

[1] 秦世伟，谷川,等.任意旋转角坐标转换的简便模型[J].工程勘察，2009，37(6)

[2] 黄桂平.多台电子经纬仪/全站仪构成混合测量系统的研究与开发[D].郑州：解放军测绘学院，1999

[3] 杨凡，李广云，王力.三维坐标转换方法研究[J].测绘通报，2010(6)

[4] 徐忠阳.工业测量系统与应用[J].计量技术，1996(6)

[5] 陈宇，白征东.基于非线性最小二乘算法的空间坐标转换[J].大地测量与地球动力学，2010，30(2)

[6] 冯其强.数字工业摄影测量技术研究与实践[D].郑州：解放军信息工程大学，2010

[7] 黄维彬.近代平差理论及其应用[M].北京:解放军出版社，1992

[8] 原玉磊，蒋理兴，刘灵杰.罗德里格矩阵在坐标系转换中的应用[J].测绘科学，2010，35(2)

[9] 杨凡，李广云，王力.一种基于罗德里格矩阵的最小二乘迭代坐标转换方法[J].工程勘察，2010，38(9)

[10] 李选福.散乱点云自动配准技术研究[D].哈尔滨：哈尔滨工业大学，2010

[11] 于起峰，尚洋.摄像测量学原理与应用研究[M].北京：科学出版社，2009

10.3969/j.issn.1000-0771.2015.08.07