两种不同势函数下半空间饱和多孔介质中Rayleigh波求解比较①

刘志军， 夏唐代， 黄 睿， 熊衍飞， 郑晴晴

( 1.浙江大学软弱土与环境土工教育部重点实验室，浙江 杭州 310058；2.浙江大学滨海和城市岩土工程研究中心，浙江 杭州 310058)

两种不同势函数下半空间饱和多孔介质中Rayleigh波求解比较①

刘志军1，2， 夏唐代1，2， 黄 睿1，2， 熊衍飞1，2， 郑晴晴1，2

( 1.浙江大学软弱土与环境土工教育部重点实验室，浙江 杭州 310058；2.浙江大学滨海和城市岩土工程研究中心，浙江 杭州 310058)

分别对“考虑两种压缩波和幅值比例系数”和“考虑一种压缩波(P1或P2波)但不考虑幅值比例系数”两种不同势函数下的半空间饱和多孔介质中Rayleigh波求解进行详细推导，理论分析表明“考虑两种压缩波和幅值比例系数”下Rayleigh波求解推导更为严密，与饱和多孔介质中存在两种压缩波的事实相一致。在研究半空间饱和多孔介质中Rayleigh波时应采用“考虑两种压缩波和幅值比例系数”的势函数。

势函数； Rayleigh波； 压缩波； 幅值比例系数； 理论分析； 数值计算

0 引言

基于20世纪50年代Biot建立的流体饱和多孔介质波动理论(简称“Biot理论”)[1]，国内外很多学者对半空间饱和多孔介质中Rayleigh波传播特性进行了研究[2-11]。Rayleigh波的能量集中在介质表面且衰减慢，在波场中占主导地位，由于Rayleigh波传播速度与介质物理力学性质密切相关，可以利用实测的Rayleigh波频散曲线反演介质的相关参数。这些特性使得Rayleigh面波法在地震勘探、地基评价、环境振动等领域得到了广泛应用。

尽管饱和多孔介质中存在两种压缩波是一个在理论和实验上均已得到验证的事实，从已有的相关文献中可以看出，半空间饱和多孔介质中Rayleigh波主要存在以下两种不同的求解：(1)势函数中考虑两种压缩波，且考虑流相和固相两者的标量势函数及矢量势函数之间的幅值比例系数[4-11]；(2)势函数中仅考虑一种压缩波，但不考虑前面提及的幅值比例系数[2-3]。

遗憾的是，迄今没有学者对上述两种不同的求解进行过理论比较或对其合理性进行过分析。另外，目前已有的文献在研究由上述两种不同势函数求解得到的Rayleigh波传播特性时均是在不同的算例(介质参数不同)下进行的，无法对两者的计算结果进行直观比较，对两者之间存在的差异程度无法做出判断。掌握半空间饱和多孔介质中Rayleigh波的正确求解对于指导Rayleigh面波法的工程应用有重要意义。

基于此，本文以自由透水边界为例，首先分别对“考虑两种压缩波和幅值比例系数”和“考虑一种压缩波但不考虑幅值比例系数”两种不同势函数下半空间饱和多孔介质中Rayleigh波求解进行详细的推导，然后从理论分析和数值计算的角度对两者进行比较，最后得出结论。

1 半空间饱和多孔介质中Rayleigh波求解

1.1 基本控制方程

根据Biot理论，u-U位移矢量形式的饱和多孔介质波动控制方程为[1]：

N▽2u+grad[(A+N)e+Qε]=

(1-1)

grad[Qe+Rε]=

(1-2)

式中，u、U分别为固相和流相绝对位移矢量；e=·u，ε=·U；b为Biot自定义的一个与达西渗透系数有关的介质耗散参数，b=n2η/κ=n2ρfg/k；g为重力加速度(m/s2)；η为流体黏滞系数(Pa·s)；κ为固体骨架动力渗透系数(m2)；k为固体骨架渗透系数(m/s)；ρ11、ρ22、ρ12分别为固相、流相质量系数和固-液质量耦合系数(kg/m3)，其中，(1-n)ρs=ρ11+ρ12，nρf=ρ12+ρ22；ρs、ρf分别为固体颗粒和流体密度(kg/m3)；A、N、Q和R为Biot弹性系数，A=λ+(α-n)2M，R=n2M，Q=n(α-n)M，N=μ，λ、μ为弹性固体骨架Lame常数，其中有：

(2)

式中，α、M为表征土颗粒和流体压缩性的Biot系数；Ks、Kb、Kf分别为固体颗粒、固体骨架和流体的体变模量(Pa)。

基于上述波动控制方程，分别对以下两种不同势函数下的半空间饱和多孔介质中Rayleigh波进行理论求解。

1.2 考虑两种压缩波和幅值比例系数

根据矢量场的Helmholtz分解定理，引入标量势φs、φf和矢量势ψs、ψf，则位移矢量u和U可表示为：

(3)

将式(3)代入式(1)，并对方程两边分别取散度和旋度，可得：

(4)

(5)

式中，P=A+2N。

结合Helmholtz分解定理和Biot理论，由矢量势和标量势所表示的应力为：

(6-1)

(6-2)

(6-3)

假设式(4)、(5)的平面波解为：

(7)

将式(7)代入式(4)、(5)，

(8-1)

(8-2)

(8-3)

(8-4)

式(8-1)两边同乘以R、式(8-2)两边同乘以Q后，两式相减，化简后可得：

(9)

式中，

(10-1)

(10-2)

将式(9)代入式(8-1)，化简后可得：

(11)

式中，

(12-1)

(12-2)

联立式(10)和式(12)，可得：

(13)

其中，

(14-1)

(14-2)

式中，υP1、υP2分别为饱和多孔介质中快纵波(P1)和慢纵波(P2)的波速理论表达式。需特别指出的是，这里的υP1和υP2并不是波传播速度(相速度)。波速理论表达式是复数形式，而波传播速度为实数，两者不能混淆，不然会得出错误结论。

求解微分方程(11)，并考虑到波应随着水平距离(x)和深度(z)的增加而呈指数衰减，其解为：

(15)

将式(15)代入式(9)，得：

(16)

式中，

(17-1)

(17-2)

由式(8-4)可得：

(18)

式中，B1、B2为流-固标量势函数幅值比例系数；B3为流-固矢量势函数幅值比例系数

将上式代入式(8-3)，并考虑到波应随着水平距离(x)和深度(z)的增加而呈指数衰减，求解可得：

(19)

(20)

式中，υS为饱和多孔介质中剪切波的波速理论表达式。

由式(15)、(16)、(18)和(19)可知，考虑两种压缩波和幅值比例系数下的势函数表达式为：

(21-1)

(21-2)

(21-3)

(21-4)

将式(21)代入式(6)，可得：

(22-1)

(22-2)

(22-3)

当半空间饱和多孔介质表面为自由透水边界，则在其表面(z=0)有：

(23)

将式(22)代入式(23)，可以得到三个关于A1、A2和A3的方程，要使得存在非零解，则其系数行列式须等于零，即：

(24)

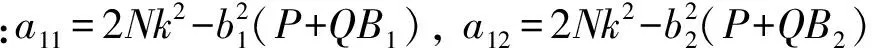
由上式可以求解出Rayleigh波的波数k(复数)，Rayleigh波传播速度c和衰减系数δ为：

(25)

1.3 考虑一种压缩波势函数但不考虑幅值比例系数

也有学者[2-3]在研究半空间饱和多孔介质中Rayleigh波时仅考虑一种压缩波(P1或P2波)，但没有考虑流相和固相两者的标量势函数及矢量势函数之间的幅值比例系数，在此种情况下，式(21)中所表示的势函数形式变为：

(26-1)

(26-2)

(26-3)

(26-4)

式中，当考虑的压缩波是P1波时，E0=E3；当考虑的压缩波是P2波时，E0=E4。

将式(26)代入式(6)，可得出应力表达式：

(27-1)

(27-2)

(27-3)

同样的，当半空间表面为透水边界时，将式(27)代入边界条件式(23)，可以得到三个关于A1、A2和A3的方程，要使得存在非零解，则其系数行列式须等于零，即：

(28)

求解上述方程，可得到Rayleigh波的波数k，由式(25)便可得出此种情况下Rayleigh波传播速度c和衰减系数δ。

2 比较

2.1 理论分析

多孔介质波传播分析的一般步骤是：① 波动控制方程→② Helmholtz分解并代入后分别取散度、旋度运算→③ 假设平面波解并求解得到势函数表达式→④ 代入由步骤②中或运用边界条件得到特征方程→⑤ 求解特征方程得到波速或波数→⑥ 波传播速度及衰减系数。

本文在“考虑两种压缩波和幅值比例系数”中，遵循上述步骤对半空间饱和多孔介质自由透水表面Rayleigh波求解进行了严密的理论推导(限于篇幅，本文对推导过程中的具体细节有所省略，详细推导过程可向作者索要)，势函数中z方向上的指数项(如iωE3z)与体波波速理论表达式(如vP1)之间的关系以及幅值比例系数(B1、B2、B3)均是推导得到，而非人为定义。我们知道饱和多孔介质中存在三种体波，即两种压缩波和一种剪切波，而由求解得到的式(21)所表示的标量势函数和矢量势函数则正好反映了这一点。

在“考虑一种压缩波但不考虑幅值比例系数”中，式(26)所表示的势函数中仅考虑了一种压缩波(P1或P2波)，这样的势函数并非问题的通解。另外，由于没有考虑幅值比例系数，存在四个振幅参数A1、A2、A3和A4。一般情况下，需有四个与A1、A2、A3和A4有关的非线性相关方程才能进行求解，而透水边界条件中只有三个方程，之所以能求解得到特征方程式(28)，原因在于将势函数式(26)代入边界条件式(23)后得到的三个方程均与A4无关，但这种情况在数理逻辑上并不严密，算是一种巧合。

因此，从理论求解推导角度上分析，相比“考虑一种压缩波但不考虑幅值比例系数”，“考虑两种压缩波和幅值比例系数”的势函数下Rayleigh波求解更为严密、合理。

2.2 数值算例

以某一具体的饱和多孔介质为例，通过数值计算对在自由透水边界下由上述两种不同的势函数求解得到的结果进行更为直观的比较，饱和多孔介质相关基本参数取值如表1所列。

图1为“考虑两种压缩波和幅值比例系数”(简称“考虑两种压缩波”)、“仅考虑P1波但不考虑幅值比例系数”(简称“仅考虑P1波”)和“仅考虑P2波但不考虑幅值比例系数”(简称“仅考虑P2波”)三种不同势函数求解下半空间饱和多孔介质中Rayleigh波传播速度和衰减系数随频率的变化曲线。

表1 饱和多孔介质基本参数

图1 不同势函数下Rayleigh波传播速度和衰减系数Fig.1 Propagation velocity and attenuation coefficient of Rayleigh wave under different potential functions

从图1(a)可以看出，由三种不同势函数求解得到的Rayleigh波传播速度在数值和变化趋势上存在明显差异。随着频率的增加，Rayleigh波传播速度“在考虑两种压缩波”时先减小后增大； “仅考虑P1波”时先是几乎保持不变后快速增大；“仅考虑P2波”时则逐渐增大。从图1(b)可以看出，由三种不同势函数求解得到的Rayleigh波衰减系数在变化趋势上完全一致，均是随着频率增大先缓慢增大后快速增大，其中，“考虑两种压缩波”和“仅考虑P2波”两种情况下Rayleigh波衰减系数在数值上也几乎相同。

从图1还可以发现，“仅考虑P1波”的Rayleigh波传播速度最大，而衰减系数最小；“仅考虑P2波”的Rayleigh波传播速度最小，衰减系数大；“考虑两种压缩波”的数值计算结果介于上述两者之中。这是因为Rayleigh波是由非均匀的平面P波和非均匀的平面SV波在一定条件下叠加产生的一种面波，而对于饱和多孔介质中的体波，P1波传播最快，衰减最慢，而P2波传播慢，衰减最快。

3 结 论

本文对两种不同势函数下Rayleigh波求解进行了理论分析，并通过数值计算对各自的结果进行了比较，数值计算结果表明由以上两种不同势函数求解得到Rayleigh波传播速度和衰减系数存在明显差异。与“考虑一种压缩波(P1或P2波)但不考虑幅值比例系数”相比，“考虑两种压缩波和幅值比例系数”的势函数下Rayleigh波的理论求解更为严密、合理，也与饱和多孔介质中存在两种体波的事实相一致。

References)

[1] Biot M A.Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid[J].Journal of the Acoustical Society of America，1956，28(2)：168-191.

[2] Jones J P.Rayleigh Waves in a Porous，Elastic，Saturated Solid[J].Journal of the Acoustical Society of America，1961，33(7)：959-963.

[3] Mei C C，Foda M A.Wave-induced Responses in a Fluid-filled Poro-elastic Solid with a Free Surface-a Boundary Layer Theory[J].Geophysical Journal of the Royal Astronomical Society，1981，66(3)：597-631.

[4] Tajuddin M.Rayleigh Waves in a Poroelastic Half-space[J].Journal of the Acoustical Society of America，1983，75(3)：682-684.

[5] 陈龙珠，黄秋菊，夏唐代.饱和地基中瑞利波的弥散特性[J].岩土工程学报，1998，20(3)：6-9.CHEN Long-zhu，HUANG Qiu-ju，XIA Tang-dai.Dispersion of Rayleigh Wave in a Saturated Soil Ground[J].Chinese Journal of Geotechnical Engineering，1998，20(3)：6-9.(in Chinese)

[6] Yang J.A Note on Rayleigh Wave Velocity in Saturated Soils with Compressible Constituents[J].Canadian Geotechnical Journal，2001，38(6)：1360-1365.

[7] 夏唐代，颜可珍，孙鸣宇.饱和土层中瑞利波的传播特性[J].水利学报，2004，11：81-84.XIA Tang-dai，YAN Ke-zhen，SUN Ming-yu.Propagation of Rayleigh Wave in Saturated Soil Layer[J].Journal of Hydraulic Engineering，2004，11：81-84.(in Chinese)

[8] 周新民，夏唐代.半空间准饱和土中瑞利波的传播特性研究[J].岩土工程学报，2007，29(5)：750-754.ZHOU Xin-min，XIA Tang-dai.Characteristics of Rayleigh Waves in Half-space of Partially Saturated Soil[J].Chinese Journal of Geotechnical Engineering，2007，29(5)：750-754.(in Chinese)

[9] Zhang Y，Xu Y X，Xia J H.Analysis of Dispersion and Attenuation of Surface Waves in Poroelastic Media in the Exploration-seismic Frequency Band[J].Gephysical Journal International，2011，187(2)：871-888.

[10] Zhang Y，Xu Y X，Xia J H.Wave Fields and Spectra of Rayleigh Waves in Poroelastic Media in the Exploration Seismic Frequency Band[J].Advances in Water Resources，2012，49：62-71.

[11] Zhang Y，Xu Y X，Xia J H，et al.On Effective Characteristic of Rayleigh Surface Wave Propagation in Porous Fluid-saturated Media at Low Frequencies[J].Soil Dynamics and Earthquake Engineering，2014，57：94-103.(in Chinese)

Comparative Study on Different Solutions to Rayleigh Waves in Half-space Saturated Porous Media under Two Different Potential Functions

LIU Zhi-jun1，2， XIA Tang-dai1，2，HUANG Rui1，2， XIONG Yan-fei1，2， ZHENG Qing-qing1，2

(1.MOEKeyLaboratoryofSoftSoilsandGeoenvironmentalEngineering，ZhejiangUniversity，Hangzhou，Zhejiang310058，China；2.ResearchCenterofCostalandUrbanGeotechnicalEngineering，ZhejiangUniversity，Hangzhou，Zhejiang310058,China)

Theoretical solutions of the Rayleigh wave in half-space saturated porous media were derived under two different potential functions corresponding to a case with two kinds of compressional waves and amplitude ratio coefficient and a case with a compressional wave (P1or P2wave) without considering the amplitude ratio coefficient，respectively.The theoretical analysis shows that the derivation of the solution of the Rayleigh waves for the case with two kinds of compressional waves and amplitude ratio coefficient is more rigorous，which is consistent with the fact that there exist two kinds of compressional waves in saturated porous media.Through numerical calculation，we compared the propagation velocities and attenuations of the Rayleigh wave in three different cases，namely，the case with two kinds of compressional waves and amplitude ratio coefficient，the case with P1wave without the amplitude ratio coefficient，and the case with P2wave without the amplitude ratio coefficient.The numerical calculation shows that there exists distinctive differences among the results obtained in the three cases above.We recommend that the potential functions that consider the two kinds of compressional waves and the amplitude ratio coefficient be applied when studying Rayleigh waves in half-space saturated porous media.

potential function； Rayleigh wave； compressional wave； amplitude ratio coefficient； theoretical analysis； numerical calculation

2014-08-20

国家自然科学基金高铁联合基金(U1234204)；国家自然科学基金面上项目(51378463)

刘志军(1988-)，男，江西吉安人，博士研究生，从事土动力学研究.E-mail：zj_lew@126.com

TU435

A

1000-0844(2015)02-0559-06

10.3969/j.issn.1000-0844.2015.02.0559