基于多因素修正的结构件疲劳寿命预估方法

朱 林 贾民平 石光林 张 菀

(1东南大学机械工程学院, 南京 211189)(2广西科技大学机械工程学院, 柳州 545006)



基于多因素修正的结构件疲劳寿命预估方法

朱 林1贾民平1石光林2张 菀1

(1东南大学机械工程学院, 南京 211189)(2广西科技大学机械工程学院, 柳州 545006)

针对传统疲劳寿命预估算法精度低且适用性窄的问题,结合工程结构件的实际特点确定了对疲劳寿命估算精度造成影响的主要因素,将影响因素量化为具体的修正因子,并在此基础上提出了一种基于多因素修正的结构件疲劳寿命预估方法.然后应用修正后的算法对实例构件的疲劳寿命进行估算,并将估算结果与应用局部应力-应变法估算的结果及台架疲劳试验结果进行对比.结果表明,修正后的算法能够实现一般大型结构件疲劳寿命的准确估算,是一类预测精度高、实施方便且具有广泛工程应用前景的疲劳寿命估算方法.

结构件;疲劳寿命;多因素;修正因子

随着科学技术的发展,人们对疲劳这一学科的认识更加深入,一系列疲劳寿命预测方法得到广泛应用:如名义应力法、局部应力-应变法、临界区域法等[1].临界区域法是一类具有工程应用前景的疲劳寿命估算方法.Karolczuk等[2]应用临界区域法将试样缺口附近区域中的应力特征参数值作为材料失效的判断准则,从而较好地解释了缺口效应的现象.应力场强法和临界距离法作为临界区域法中常见的两类方法已得到一些应用.但这些应用大多只针对平面结构,而以结构件作为分析对象的还很少.

工程实际中则更倾向于使用名义应力法和局部应力-应变法.传统名义应力法的核心是分析零件的最大应力,将最大应力与材料的应力寿命S-N曲线相结合来估算疲劳寿命.Tevatia等[3]将传统名义应力法与有限元技术相结合有效地实现了板材复杂受力情况下疲劳寿命的预估.这种方法的最大优点是分析步骤简单、适用面广且实用性强.但由于结构件与材料试样间的疲劳性能参数存在差异,故疲劳寿命的估算精度无法得到保证.

局部应力-应变法以应变分析为基础,用应变寿命σmax-N曲线代替S-N曲线来预测疲劳寿命.Lim等[4]应用局部应力-应变法对大应变条件下试样的疲劳寿命进行了预估.局部应力-应变法的估算精度较高,但其适用面较窄.

本文结合工程结构件的实际特点确定了结构件中对疲劳寿命造成影响的主要因素,将这些因素量化为具体数值的修正因子,并基于多个修正因子提出了基于多因素修正的结构件疲劳寿命预估方法.最后通过实例分析介绍了这一算法的具体分析流程,并对这一疲劳寿命预测方法的可行性和分析准确性进行了验证.

1 多因素修正的疲劳寿命预估算法

影响疲劳寿命的因素很多,大致可分为可控因素和不可控因素.不可控因素受到环境、人为因素等的影响,难以量化.而可控因素主要包括残余应力、结构件应力集中、结构件尺寸及表面加工处理方式[5].因此,定量分析上述因素对准确预测结构件疲劳寿命是非常必要的.

1.1 残余应力对疲劳寿命的影响

残余应力会改变受载结构件的应力状态,从而对结构件的疲劳寿命造成影响.

平均应力和分析强度的关系[6]可描述为

(1)

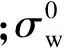
(2)

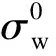
1.2 应力集中对疲劳寿命的影响

应力集中会影响受载结构件的应力状态,从而影响结构件的疲劳寿命.应力集中因子是判别影响程度的指标.常见应力集中因子的获取方法包括计算法和测量法.测量法是基于弹性变形实现的,主要适用于材料试样,但对大型结构件来说并不合适.文献[8]研究发现,将有限元法与数值模拟相结合是计算大型构件应力集中因子最合适的方法.其具体求解过程如下.

① 对结构件进行分析以确定其最大应力,沿最大应力横截面选取反映应力场分布的积分路径.

② 在积分路径上取点,即可获得应力根部截面方向上点距L与名义应力s之间的对应值,通过拟合上述数据即可获得对应的应力场函数表达式.

③ 将应力场函数表达式代入下式,求解与应力场所对应的名义应力:

(3)

④ 将名义应力代入下式,获得结构件所对应的应力集中因子:

(4)

式中，smax为最大名义应力.为验证上述方法的精度,本文运用有限元分析的方法对B/b=2,ρ/b=0.16(其中，B为材料试样宽度,ρ为圆角半径,b为最小横截面宽度)的Q345b材料试样进行分析,所得的应力集中因子为1.539,而通过文献[9]查得的应力集中因子为1.551,误差为0.77%.从而说明通过有限元方法所获得的应力集中因子的精度是可以保证的.

1.3 结构件尺寸对疲劳寿命的影响

结构件尺寸因子是表示结构件尺寸对疲劳寿命影响的参数.结构件的疲劳极限σ0r与材料的疲劳极限σr之间的关系可表示为

(5)

式中,f(x1,x2)为反映局部最大应力附近应力场的函数;x1及x2为平面场的坐标参数.

应力场函数可通过应力场中应力路径下某点与最大局部应力根部的距离Li来表示,即

(6)

当构件1与构件2材料相同时,满足相似性原理的两构件之间尺寸因子可表示为

(7)

联合式(5)～(7)可得到尺寸因子计算式,即

(8)

式中,a1,a2,a3,a4及b1,b2,b3,b4表示拟合函数表达式中的系数.如式(8)所示,结构件尺寸因子为结构件与参照标准试样间应力场函数积分的比值.

1.4 表面加工处理方式对疲劳寿命的影响

不同的表面处理方式对构件应力状态的影响是不同的,故也会对疲劳寿命造成不同的影响.这里所指的表面处理方式通常是指机加工完成后的处理方式,主要包括淬火、高频淬火、表面氮化处理、渗碳处理、滚压、喷丸等.常见处理方式所对应的表面质量系数[10]如表1所示.

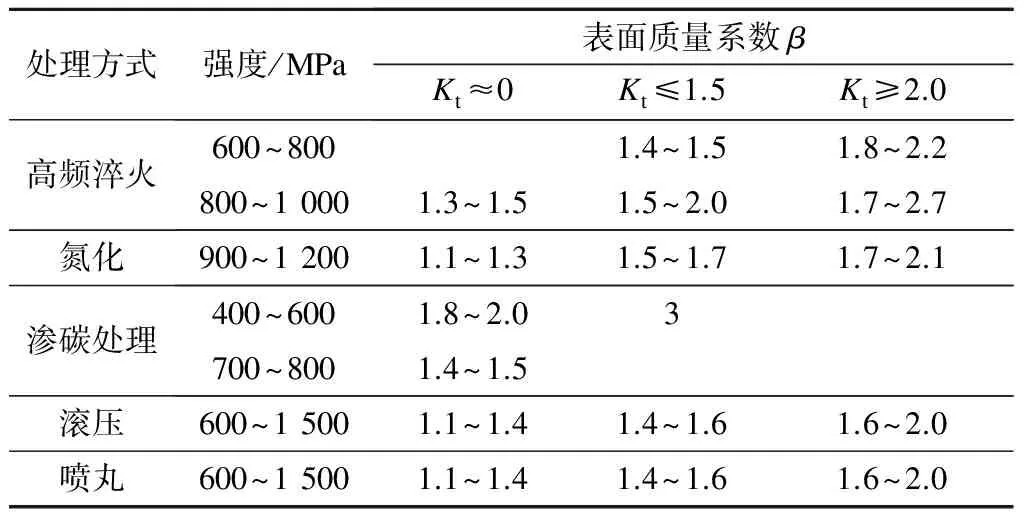
表1 常见处理方式所对应的表面质量系数

1.5 多因素修正后的疲劳寿命预估算法

传统名义应力法的计算方法可表述为

SmN=C

(9)

式中，S为应力.结合上述各因素对应力状态的影响,即可建立基于多因素修正的疲劳寿命预估算法，即

(10)

式中,N为疲劳寿命;m,C为与材料、应力比有关的参数.

通过式(10)的计算不仅可以实现材料试样疲劳寿命的预测,还能实现一般结构件疲劳寿命的估算.

2 疲劳寿命预估实例

为进一步说明基于多因素修正的疲劳寿命预估方法的实施步骤并验证其预测疲劳寿命的精确程度,本文以装载机后桥壳为例对其疲劳寿命进行预估,其实施流程如图1所示.

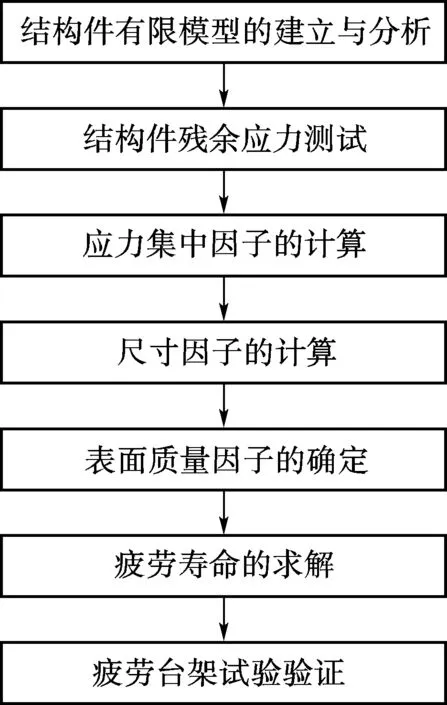
图1 分析方法的实施流程图

2.1 桥壳有限元模型的建立与分析

载荷谱是构件疲劳寿命分析的基础,故首先需要获得桥壳的模拟载荷谱.利用Pro-E软件建立桥壳的三维模型,并将其导入ANSYS软件中.设置材料为Q345b,待前处理设置完毕后对3种典型恶劣工况[11]下的应力状态进行求解,即可得到如表2所示的计算结果.由表可见,最大应力出现在工况3,其最大等效应力为259.1 MPa.由于疲劳寿命取决于应力幅值的大小,因此后续疲劳寿命的分析只需以工况3为分析对象.如图2所示,工况3的等效最大应力出现在桥壳支撑处.

表2 桥壳有限元强度计算结果

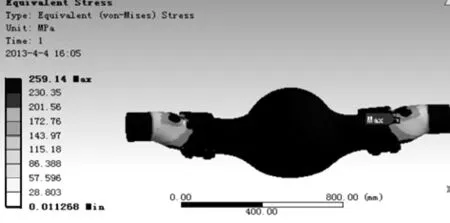
图2 桥壳工况3的应力云图

2.2 结构件残余应力的测试

根据有限元分析的结果,确定测点的分布如图3所示.为保证测量精度,每个测量位置测量3次.

图3 测点分布

Q345b材料的最佳测量方法为侧倾固定ψ法,定峰方法为交相关法,其他设置参数如表3所示.如图4所示,采用X射线残余应力测试设备对桥壳进行测试,得到如表4所示的对应于桥壳测点的残余应力测量结果.桥壳左右两侧测点的残余应力分布如图5所示.由图可见,对应于桥壳弯角区域的残余应力偏大.

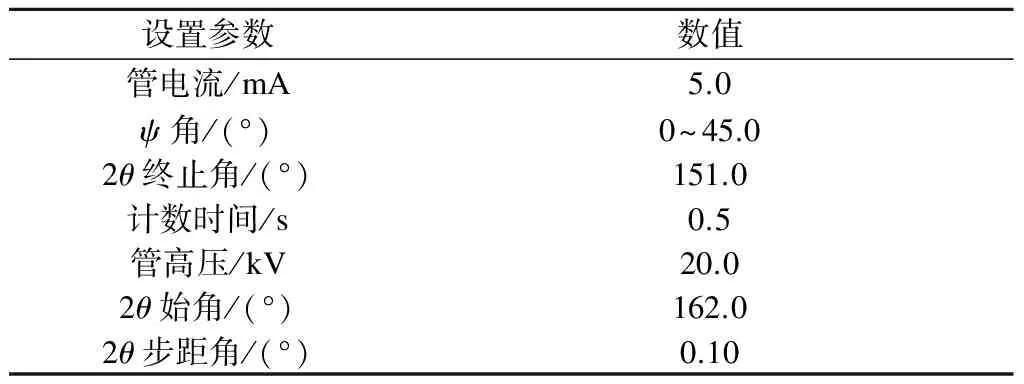
表3 X射线残余应力设置参数

图4 残余应力测定

最后,将所有测点的残余应力和有限元分析中所对应的最大等效应力代入式(2),修正后的最大应力值为276.1 MPa.

2.3 应力集中因子的计算

据有限元分析结果,沿最大应力根部横截面方向选取积分路径,并在积分路径上按距取点,即可获得点距L与名义应力s之间的对应值(见表5).

(a) 测点A～C

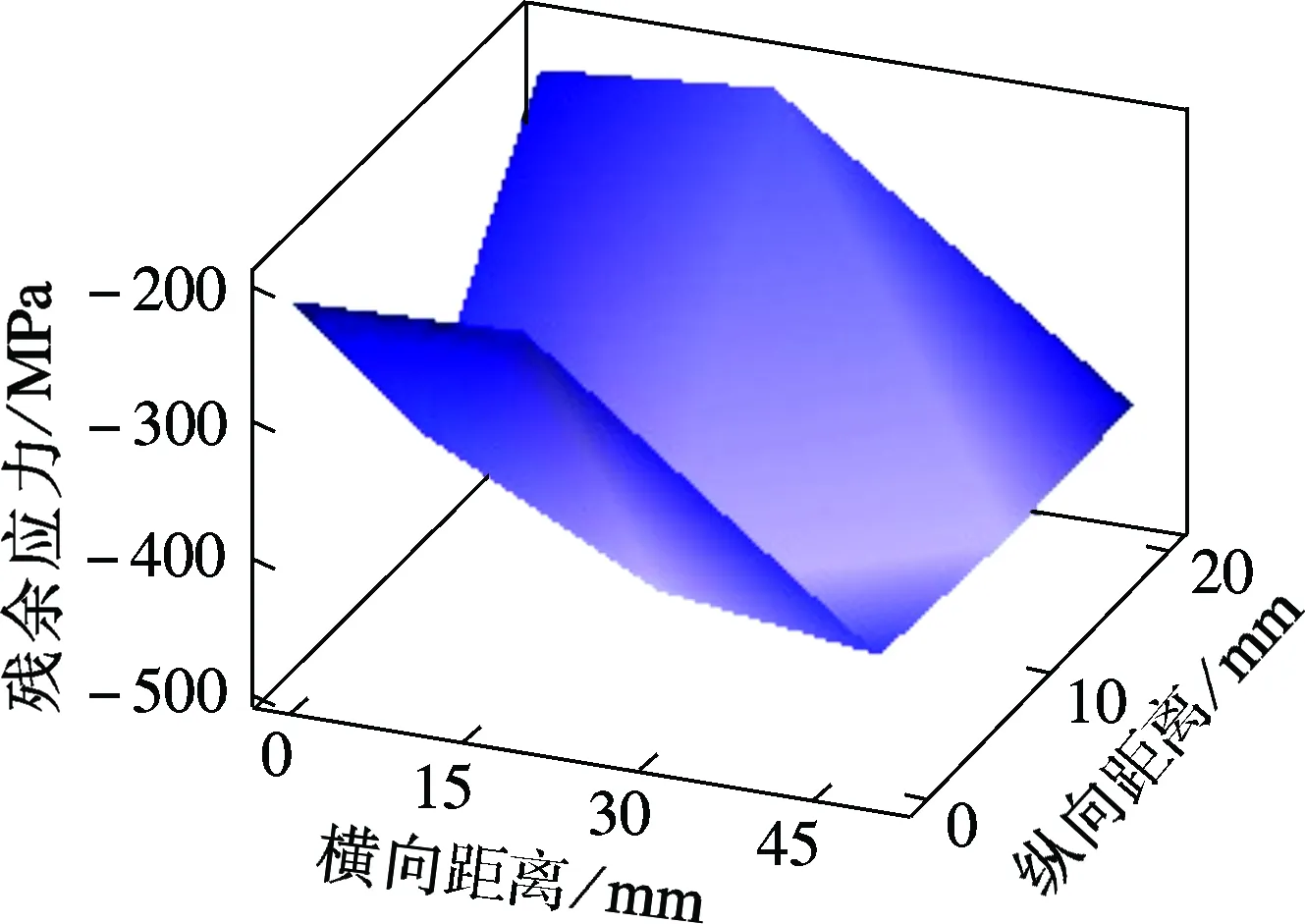
(b) 测点D～F

L/mm257．510203040s/MPa259．1211．7177．7151．33139．672．135．735．1

对表5数据进行拟合,得到

y=p1L4+p2L3+p3L2+p4L+p5

(11)

式中,p1=0.000 312 85,p2=-0.027 988,p3=0.973 98,p4=-19.815,p5=254.85.式(11)即为最佳拟合函数方程.将式(11)代入式(3)和(4),即得到桥壳的应力集中因子为2.016.

2.4 尺寸因子及表面质量因子

将2.3节中的计算结果与Q345b所对应的材料参数代入式(8),计算出尺寸因子为0.970 25.桥壳表面经喷丸处理且Kt≥2.0,查阅表1，即可得表面质量系数为1.6.

2.5 疲劳寿命的求解

将修正因子及材料参数代入根据修正算法编制的软件中,求解桥壳疲劳寿命.同时,为了对分析的准确性进行评估,使用局部应力-应变法对桥壳的疲劳寿命进行估算,结果如表6所示.

表6 疲劳寿命估算结果 万次

2.6 弯曲疲劳台架试验

如图6(a)所示,对桥壳进行垂直弯曲疲劳试验,获得如表7所示的疲劳试验数据.由表可见,桥壳直至断裂的平均疲劳寿命为116.223 7万次,与基于多因素修正的疲劳寿命分析结果基本吻合.

(a) 桥壳疲劳试验台架

(b) 桥壳断裂件

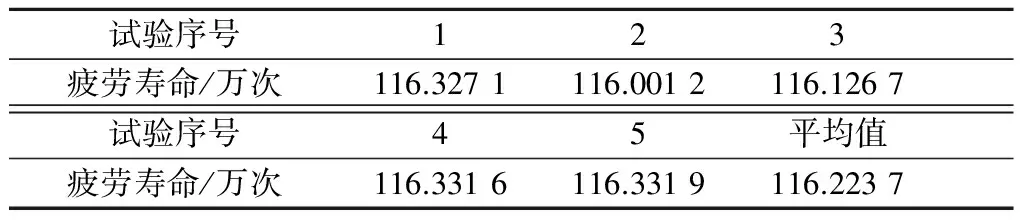
试验序号123疲劳寿命/万次116．3271116．0012116．1267试验序号45平均值疲劳寿命/万次116．3316116．3319116．2237

同时,对比图6(b)和图2即可发现，桥壳的断裂位置与有限元分析最大应力位置完全重合.

3 结论

1) 针对传统疲劳寿命估算方法精度低且适用性窄的问题,在研究对结构件疲劳寿命造成影响因素的基础上,通过引入修正因子提出了基于多因素修正的疲劳寿命预估算法.

2) 实例验证表明，本文提出的基于多因素修正的疲劳寿命预测算法的预测结果与台架试验结果基本吻合,且预测精度优于局部应力-应变法.从而证明该预测方法是可行的,且提高了预测结果的精度.

3) 基于多因素修正的疲劳寿命分析方法不仅增加了分析数据的可靠性,而且为结构件疲劳寿命预估提供了新的技术路径.

References)

[1]Gagg C R, Lewis P R.In-service fatigue failure of engineered products and structures—case study review [J].EngineeringFailureAnalysis, 2009, 16(6): 1775-1793.

[2]Karolczuk A, Macha E. Selection of the critical plane orientation in two-parameter multiaxial fatigue failure criterion under combined bending and torsion [J].EngineeringFractureMechanics, 2008, 75(3/4): 389-403.

[3]Tevatia Abhishek, Srivastava Sunil Kumar. Modified shear lag theory based fatigue crack growth life prediction model for short-fiber reinforced metal matrix composites[J].InternationalJournalofFatigue, 2015, 70(1): 123-129.

[4]Lim Jae-Yong, Hong Seong-Gu, Lee Soon-Bok. Application of local stress-strain approaches in the prediction of fatigue crack initiation life for cyclically non-stabilized and non-Masing steel [J].InternationalJournalofFatigue, 2005, 27(10/11/12): 1653-1660.

[5]Kotousov A, Chang D.Theoretical and experimental study of fatigue growth of interacting cracks[J].InternationalJournalofFatigue, 2015, 70(1): 130-136.

[6]Ikushima Kazuki, Shibahara Masakazu. Prediction of residual stresses in multi-pass welded joint using idealized explicit FEM accelerated by a GPU[J].ComputationalMaterialsScience, 2014, 93(10): 62-67.

[7]万鑫,詹科,姜传海.X射线衍射方法分析粗晶铁硅合金的残余应力[J].机械工程材料,2014,38(6):95-99. Wan Xin, Zhan Ke, Jiang Chuanhai. Analysis of residual stress in coarse-grained Fe-Si alloy by X-ray diffraction[J].MaterialsforMechanicalEngineering, 2014, 38(6): 95-99. (in Chinese)

[8]Carter B J, Schenck E C, Wawrzynek P A, et al. Three-dimensional simulation of fretting crack nucleation and growth[J].EngineeringFractureMechanics, 2012, 96(3): 447-460.

[9]王滨.ASTM金属材料拉伸试验方法介绍[J].理化检验：物理分册,2004,40(9):477-480. Wang Bing. Brief introduction of tension test specimen of metallic materials of ASTM[J].PhysicalTestingandChemicalAnalysisPartA:PhysicalTesting, 2004, 40 (9): 477-480. (in Chinese)

[10]Petrucci G, Zuccarello B. Fatigue life prediction under wide band random loading [J].Fatigue&FractureofEngineeringMaterials&Structures, 2004, 27(12): 1183-1195.

[11]刘良臣,石光林.装载机维修图解手册[M].南京:江苏科学技术出版社,2007:156-161.

Estimation approach study of structural fatigue life based on multiple factors correction

Zhu Lin1Jia Minping1Shi Guanglin2Zhang Wan1

(1School of Mechanical Engineering, Southeast University, Nanjing 211189, China) (2School of Mechanical Engineering, Guangxi University of Technology, Liuzhou 545006, China)

To solve the low accuracy and narrow application of traditional estimation approaches, the main factor affecting the estimation accuracy of fatigue life are determined according to practical characteristics of engineering structures. These factors are quantified as the concrete correction coefficients. Then, estimation approach of structure fatigue life based on multiple factors correction is proposed. The fatigue life of an instance is estimated by this corrected estimation approach. The estimation results are compared with those of the local stress-strain method and the fatigue test data. It is shown that this corrected approach can accurately estimate the fatigue life of general large structures. It has high estimation accuracy, convenient implementation and extensive engineering application prospects.

structure; fatigue life; multiple factors; correction factor

10.3969/j.issn.1001-0505.2015.03.010

2014-11-29. 作者简介: 朱林(1989—)，男，博士生；贾民平(联系人)，男，博士，教授，博士生导师,mpjia@seu.edu.cn.

国家自然科学基金资助项目(51075070)、高等学校博士学科点专项科研基金资助项目(20130092110003).

朱林,贾民平,石光林,等.基于多因素修正的结构件疲劳寿命预估方法[J].东南大学学报:自然科学版,2015,45(3):469-473.

10.3969/j.issn.1001-0505.2015.03.010

V263.5

A

1001-0505(2015)03-0469-05