轴对称二次非球面镜面几何参数的算法

杜建祥,宗肖颖

(北京空间机电研究所,北京 100190)



轴对称二次非球面镜面几何参数的算法

杜建祥,宗肖颖

(北京空间机电研究所,北京 100190)

在现代的空间光学遥感器中，越来越多地使用二次非球面光学元件代替以往的球面光学元件，消除球面镜不能消除的像差。二次非球面的几何参数包括其顶点曲率半径和非球面系数，它们对相机的性能有着重要的影响。三座标仪的使用使得二次非球面几何参数的测量变得方便快捷。在三坐标测量数据基础上，给出了一种新型的二次非球面几何参数计算方法，通过采集座标点、寻找旋转轴、计算法线像差等步骤求解出顶点曲率半径和非球面系数。通过仿真分析和实验验证，顶点曲率半径的计算精度可达0.01%，非球面系数的精度可达0.0002。

光学测试；几何参数；非球面系数；顶点曲率半径；二次曲面

引言

随着现代光学遥感器的发展，大口径、长焦距、高像质成为了发展趋势，这使得光学元件的光学面从原来的球面向二次非球面转变。使用二次非球面的光学元件表面能够有效地防止轴外像差的产生，对提高光学镜头的像质有着重要的作用。现在二次非球面的加工技术已经非常成熟，其使用已经非常广泛。二次非球面的几何参数检测主要包括顶点曲率半径的检测和二次非球面系数的检测，几何参数对光学镜头的焦距、像质有着重要的影响。现在国内对此最常用的方法是无像差法，就是在无像差法面形测试光路中使用标准的量杆加刀口的方法实现二次非球面2个焦点距离及长轴或者短轴的测试，这种方法有较高的精度，但是对操作人员的要求较高，对刀口的定位、对量杆操作的把握会引起测量误差，如果测试环境有较大的气流，会影响无像差法面形测试光路的调整，这也会带来测试误差。使用三坐标测量仪测试二次非球面镜面的点座标，根据这些座标计算其顶点曲率半径和非球面系数，这样在实现稳定的高精度测试的同时，对人员要求及操作环境的要求也降低了，提高了测试效率。本文介绍了基于三座标测试数据的计算顶点曲率半径和非球面系数的算法。包括采集座标点、拟合曲面、寻找旋转轴、求解顶点曲率半径和非球面系数e2的步骤。根据仿真和实验数据，本算法能够满足多数情况下的测试精度要求。

1 算法介绍

1.1 最小二乘曲面拟合

根据三坐标测量仪得到的坐标数据，适用最小二乘曲面拟合算法计算出二次非球面一般方程的系数，二次非球面的一般三维曲面方程为

F(x,y,z)=x2+a2y2+a3z2+a4xy+

a5xz+a6yz+a7x+a8y+a9z+a10=0

(1)

由此可得到误差函数：

(2)

为了使得E达到最小，它应满足下列极值的必要条件：

(3)

由这个必要条件得到了关于aj(j=2,3,4,5,6,7,8,9,10)的一组包含9个方程的线性方程组，由此就能解出各个aj的值。

1.2 顶点曲率半径和二次非球面系数的计算

在二维情形中，关于二次曲线有一个重要的性质[1]：

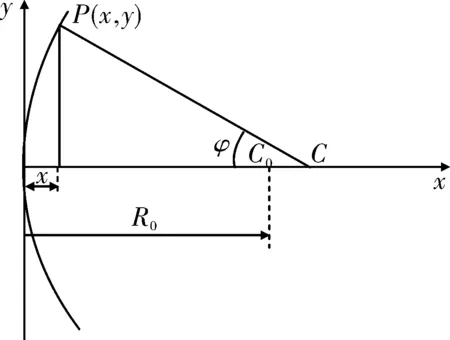
图1 二次曲线示意图Fig.1 Conic curve

图1中，P(x,y)是二次曲线上的任意一点，C为P点法线和x轴的交点，C0是曲线顶点的曲率中心，R0为曲线的顶点曲率半径，φ为P点法线和x轴的夹角,有：

(4)

再回到三维情形中，图1中的x轴就是二次曲面的顶点法线，也是曲面的旋转对称轴。φ就是二次曲面上一点P(x,y,z)的法线和其旋转对称轴的夹角，由(4)式可知，只要知道二次曲面上任意2个点的φ值，就能够求出R0和e2。由此可进行以下步骤：

1) 获得曲面F(x,y,z)的旋转对称轴

在曲面F(x,y,z)的包含其顶点的有限区间里任意取一点P0(x0,y0,z0)，其法向量为

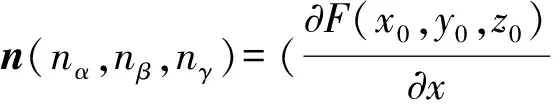
(5)

此法向量的直线方程为

(6)

在曲面上取一点P1(x1,y1,z1)，可求得P1关于P0点法线的对称点P2(x2,y2,z2)。

假设：

(7)

则有：

x2=2(x0+nαt)-x1

y2=2(y0+nβt)-y1

z2=2(z0+nγt)-z1

(8)

再将P2(x2,y2,z2)带入曲面方程F(x,y,z)=0，可得到

ε=|F(x2,y2,z2)|>0

(9)

可设定一个允许的ε值，如果|F(x2,y2,z2)|小于这个允许值，就可以认为P2(x2,y2,z2)在曲面上，此时应该再选择一点P3(x3,y3,z3)，过P1点做P0点法线的垂线L1，过P3点做P0点法线的垂线L2，L1和L2垂直，因为此时的ε值对是否旋转对称最为敏感，同理求得P3的关于P0点法线的对称点P4，得到|F(x4,y4,z4)|，如果|F(x2,y2,z2)|和|F(x4,y4,z4)|有一个大于最大允许的ε值，那就继续计算下一个P0点。如果|F(x2,y2,z2)|和|F(x4,y4,z4)|同时小于最大允许的ε值，那么P0就为此曲面的顶点，其法线就是曲面的顶点法线，也是曲面的旋转轴。

2) 计算顶点曲率半径和二次非球面系数e2

确定了曲面顶点P0(x0,y0,z0)和顶点法线n=(nα,nβ,nγ)后，在曲面上再取两点A(xa,ya,za)和B(xb,yb,zb)，可得到A、B两点的法线向量分别为

(10)

得到na、nb和n的夹角正切值为

(11)

(12)

计算A、B两点在P0法线上的垂足，设

(13)

则两垂足分别为

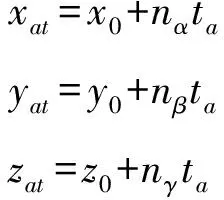
(14)

得到A、B两点关于P0的轴向和径向距离分别为

轴向：

(15)

径向：

(16)

最后可得此二次曲面的顶点曲率半径e2和R0分别为

(17)

(18)

2 算法仿真结果

旋转对称二次非球面无平移和倾斜量时的三维方程为

x2+y2=2R0z-(1-e2)z2

(19)

将其延x和y方向分别平移3 mm和2 mm，并且绕x轴旋转0.1°，参数设置如表1所示。

表1 二次非球面参数设置

用matlab进行采样取点，采样数为1 600个。使用第2节中的算法进行计算，得到结果如表2所示。

表2 通过采样点计算得到的二次非球面参数

Table 2 Conic aspheric surface parameters calculated with sample points

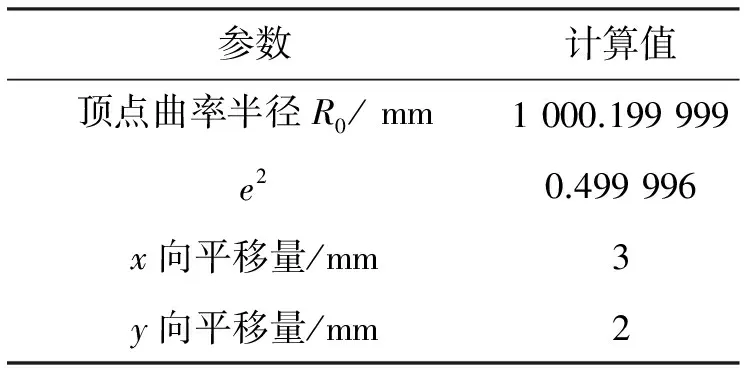
参数计算值顶点曲率半径R0/mm1000．199999e20．499996x向平移量/mm3y向平移量/mm2

计算得到的参数值和实际值相差很小，在使用过程中已经完全可以忽略，验证了此算法的可行性。

3 实验验证

使用本算法对下列5块凹非球面镜S1-S5进行验证测试。其参数如表3所示。

表3 被测凹二次非球面镜参数

Table 3 Parameters of concave conic aspheric surface under test

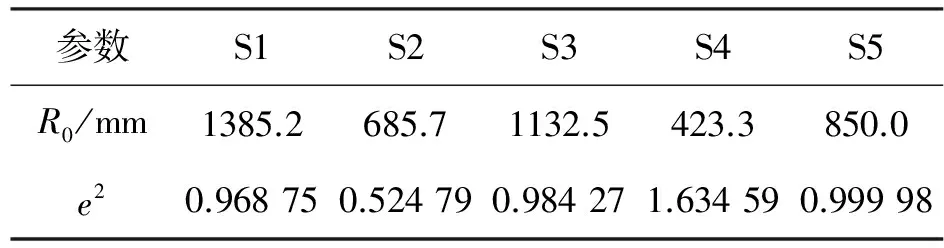
参数S1S2S3S4S5R0/mm1385．2685．71132．5423．3850．0e20．968750．524790．984271．634590．99998

首先使用三座标仪进行这些镜面进行采点，采点范围为口径100 mm的镜面点，采点数500个。根据这些座标点，通过本算法计算得到非球面顶点曲率半径R0和非球面系数e2分别如表4所示。

表4 通过本算法计算得到的被测凹二次非球面镜参数

Table 4 Parameters of concave conic aspheric surface calculated with our algorithm

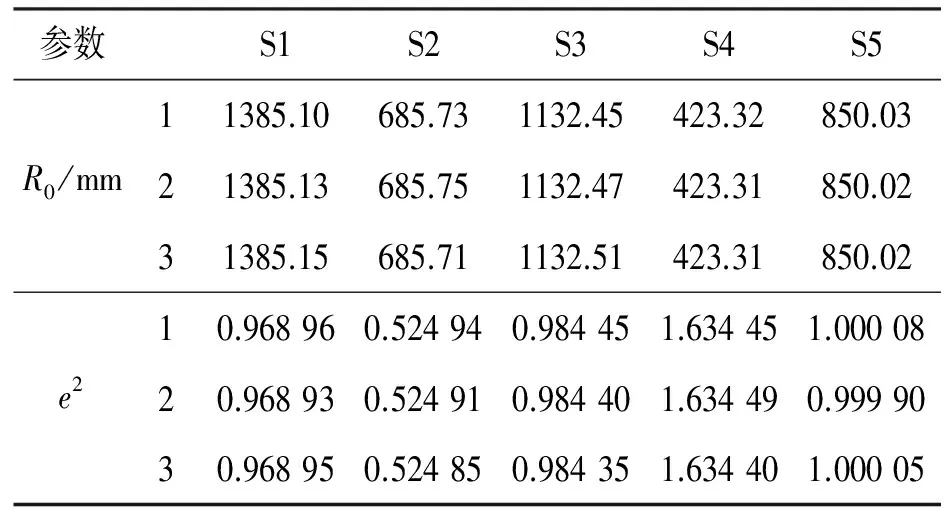
参数S1S2S3S4S5R0/mm11385．10685．731132．45423．32850．0321385．13685．751132．47423．31850．0231385．15685．711132．51423．31850．02e210．968960．524940．984451．634451．0000820．968930．524910．984401．634490．9999030．968950．524850．984351．634401．00005

表5 凹二次非球面镜参数测试误差

Table 5 Test errors of parameters of concave conic aspheric surface

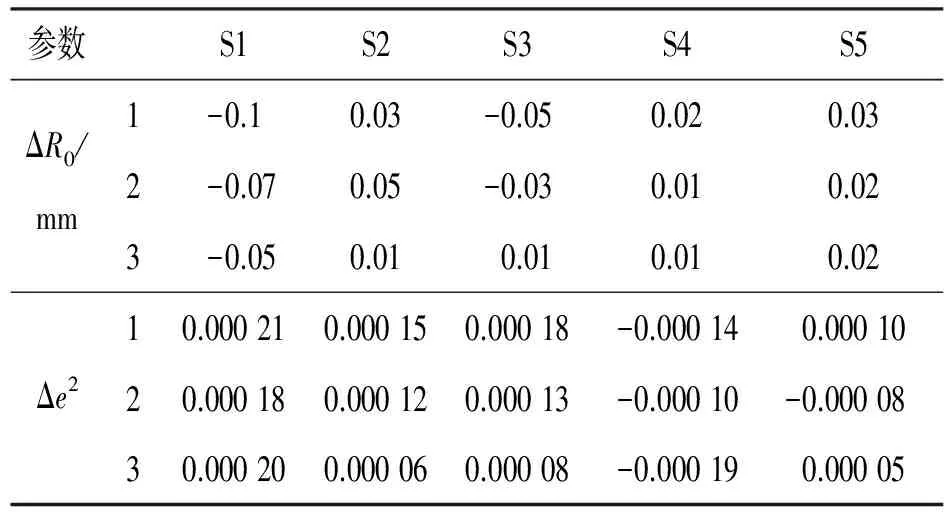
参数S1S2S3S4S5ΔR0/mm1-0．10．03-0．050．020．032-0．070．05-0．030．010．023-0．050．010．010．010．02Δe210．000210．000150．00018-0．000140．0001020．000180．000120．00013-0．00010-0．0000830．000200．000060．00008-0．000190．00005

从表5中可看出顶点曲率半径R0和二次曲面系数e2的测试精度已经很高，测试误差主要包含了三座标仪测试误差和本算法中的一些近似处理带来的误差。二次曲面系数e2对镜面点座标的测试误差比较敏感，需要多次测量才能够达到比较好的重复性。综合来说，顶点曲率半径R0测试精度可达到0.01%，非球面系数测试精度可达到0.000 2。

4 结论

为了提高二次非球面几何参数的测试效率，本文提出了基于三座标测试数据的几何参数计算算法，并详细给出了算法实现过程，再通过仿真及实测数据，表明了算法的可行性。实验数据表明，顶点曲率半径测试精度为0.01%，非球面系数测试精度为0.000 2，该测试精度已经能够满足使用要求。

[1] Pan Junhua. The design,manufacture and test of the aspherical optical surfaces[M]. Suzhou:Suzhou University Press,2004:5-6. 潘君骅.光学非球面的设计、加工与检验[M].苏州：苏州大学出版社，2004:5-6.

[2] Sha Dingguo, Quan Shuxue, Zhu Qiudong, et al. An optical asphericity definition and its accurate calculation[J].Acta Photonica Sinica, 1995, 24(1):91-95. 沙定国，全书学，朱秋东，等.光学非球面度的定义及其准确计算[J].光子学报，1995，24(1):91-95.

[3] Liu Huilan,Sha Dingguo,Hao Qun,et al. A method of high order asphericity definition[J].Opto-Electronic Engineering, 2004, 31(6):44-47. 刘惠兰，沙定国，郝群，等.一种高次光学非球面度的计算方法[J].光电工程，2004，31(6):44-47.

[4] Mathematics Department of Tongji Univercity. Higher mathematics[M]. Beijing: Higher Education Press,2004:95-125. 同济大学应用数学系.高等数学[M].北京：高等教育出版社，2004:95-125.

[5] Shi Wanming, Yang Huafei, Wu Yushu, et al. Numerical analysis[M]. Beijing: Beijing Institute of Technology Press,2002:30-65. 史万明，杨骅飞，吴裕树, 等.数值分析[M].北京：北京理工大学出版社，2002:30-65.

[6] Chen Qinfang,Xu Changjie. Coaxial measurement of axisymmetric aspheric lens[J].Journal of Applied Optics,2008,29,(6):870-873. 陈钦芳,徐昌杰.轴对称非球面透镜光轴共轴度的测量研究[J]. 应用光学，2008,29(6):870-873.

[7] Wang Shengyun,Zheng Xue,Zhang Mei. Testing technology for aspheric wavefront aberration[J]. Journal of Applied Optics, 2006,27(sup.): 65-67. 王生云,郑雪,张玫.非球面波像差的检测技术[J]. 应用光学, 2006,27(增刊): 65-67.

[8] Wang Hongjun,Tian Ailing,Du Yujun. Determination of aspheric reference sphere by tri-point method[J]. Journal of Applied Optics,2004,25(4):63-65. 王红军,田爱玲,杜玉军. 非球面最适球面的确定方法——三点法[J]. 应用光学,2004, 25(4):63-65.

[9] Duan Cunli,Tian Ailing,Chen Zhichao. Simulation calculation of measuring optical aspheric surface based on light pattern projection[J]. Journal of Applied Optics, 2004,25(5): 62-66. 段存丽,田爱玲,陈志超.光学非球面器件检测新方法探究[J].应用光学, 2004,25(5): 62-66.

[10]Yang Pengli. Elimination method of adjustment error in measurement of aspheric optical elements[J]. Journal of Applied Optics, 2006,27(sup.):58-60. 杨朋利. 非球面光学零件测量中调整误差消除方法[J]. 应用光学,2006,27(增刊):58-60.

Algorithm for calculating geometric parameter of axial symmetry conic surface

Du Jianxiang，Zong Xiaoying

(Beijing Institute of Space Mechanics & Electricity,Beijing 100190,China)

Modern space telescopes use conic surfaces rather than sphere surfaces in optical systems to avoid the unnecessary aberration brought by sphere surfaces. Geometric parameters of conic surfaces include the vertex radius and aspheric coefficient (e2), they are significant to the performance of the telescopes. As the coordinate measuring machine (CMM) is widely used, the measurement for the geometric parameters of conic surface is much more convenient. We introduced a new algorithm for calculating vertex radius ande2based on the data measured by the CMM through a few steps: measuring the coordinates, finding the axis and calculating the normal aberration theory. According to the simulation and experiment, the error of vertex radius is less than 0.01%, the error ofe2is less than 0.0002,which can meet the demands for most measurements.

optical test; geometric parameters; aspheric coefficient; vertex radius; conic surface

1002-2082(2015)06-0900-05

2015-05-12；

2015-09-17

杜建祥(1984-)，男，浙江嵊州人，硕士，工程师，主要从事光学装调测试工作。E-mail：13911017584@163.com

TQ171

A

10.5768/JAO201536.0602004