药物经皮吸收数学模型研究进展
何星垚,王 晖
(广东药学院中药学院,广东 广州 510006)
药物经皮吸收数学模型研究进展
何星垚,王 晖
(广东药学院中药学院,广东 广州 510006)
经皮给药是一种能避免肝脏的首过效应及肠胃灭活、维持血药浓度、提高生物利用度的给药途径。而药物经皮吸收需透过角质层、活性表皮层、真皮层的屏障。近年来,随着计算机技术的发展,根据药物的不同理化特性及皮肤各层的生理特征,建立了许多预测药物经皮吸收方面的数学模型。该文就预测药物经皮吸收数学模型的研究进展进行了综述。
经皮吸收;透皮吸收;预测药物经皮吸收;数学模型;透皮系数;经皮给药;经皮转运
皮肤药理学(dermatopharmacology) 作为药理学的一个新分支,其主要任务是研究药物对皮肤的作用及作用机制、药物在皮肤的影响下所发生的变化及变化规律,以及药物的经皮吸收特性等。经皮给药是一种能避免肝脏的首过效应及肠胃灭活、维持血药浓度、提高生物利用度的给药途径,越来越引起医药界的重视。近年来,随着计算机技术的发展,根据药物的不同理化特性及皮肤各层的生理特征,建立了许多预测药物经皮吸收方面的数学模型,并逐步成为经皮给药制剂研究的有用工具。
1 药物经皮吸收的概况
经皮给药是药物通过皮肤吸收的一种方法,具有保持血药浓度、避免首过效应、改善患者顺应性与安全性等优点[1]。
药物分子进入体循环的过程中可能经过的物理变化与化学变化见Fig 1[2],药物透过角质层一般可通过以下3种途径:跨细胞通路、细胞间通路与皮肤附属器通路[3](Fig 2[4])。对于亲脂性的小分子药物(r<4Å, KO/W>1),更趋向于细胞间通路的自由体积扩散;对于亲脂性的大分子药物(r>4Å,

Fig 1 Physical and chemical changes that drug percutaneous delivery relates to
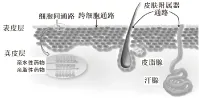
Fig 2 Passages of percutaneous delivery
KO/W>1),更趋向于细胞间通路的径向扩散;对于水溶性的药物(KO/W<1),大分子药物更趋向于皮肤附属器通路(KO/W<0.01),小分子药物更趋向于细胞间通路透过角质层[5]。小分子药物或离子型化合物也可经跨细胞通路进入体内,但药物通过速率很慢,甚至被细胞吸附而消除,但在促透剂辅助下,其跨细胞转运速率大大增加[3]。目前,评价药物经皮吸收效率主要是看皮肤的透皮系数,测量药物透皮系数需要用到哺乳动物的离体皮肤,而人类以外的哺乳动物由于毛孔密度比人体大,因而结果会有一定偏差。此外,测量透皮系数耗时长,用于筛选药物的效率低。使用数学模型初步筛选药物具有成本低、测量时间短的优点,是一种比较有前景的方法。数学模型用于预测药物透皮吸收能力主要是通过研究分配系数、扩散系数与药物透皮进入体内的路径长度之间的关系[6]。
2 经角质层转运模型
角质层厚度约为10~30 μm,由多层已退化的僵硬扁平角化细胞经紧密排列而成,细胞内充满致密的角蛋白丝与丝聚蛋白,细胞外包被着角质化的细胞被膜,这些细胞被膜能有效地防止外界化合物进入细胞[4],细胞间隙由多层高度有序排列的致密脂质双分子层交替组成,该双分子层主要含神经酰胺、脂肪酸、胆固醇、甘油三脂等脂质[7-8](Fig 3[3]),这些性质决定了角质层是外源性物质进入体内的主要屏障[9],而由于细胞内致密的蛋白与纤维,药物透皮吸收主要是通过细胞间质进入体内。
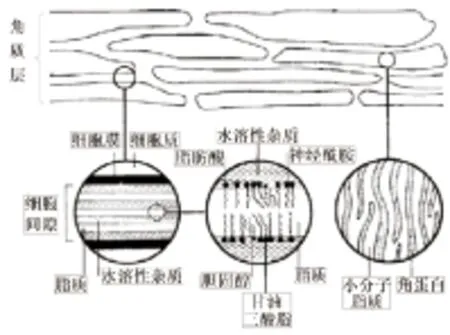
Fig 3 Microstructure of stratum corneum
2.1 经细胞间隙转运
2.1.1 网络模型 基于细胞间脂质的微观结构,Schumm等[10]建立一个含580个节点、3903条边的网络,连接两个节点的边可加速药物分子的转移,并基于该网络建立三个模型描述药物分子在不同细胞间的转移过程,以计算机模拟方法得到不同浓度的药物从细胞间通路进入体内的动力学过程:
一般模型:描述药物分子呈线性关系转移的过程,类似传统的菲克扩散。以NA表示在节点A中药物分子的数量,HEB表示节点B中高能量分子的数量,SAB表示节点A与节点B之间的接触面积,D表示扩散系数,SBtot表示节点B与其相邻节点的总接触面积,RB表示节点B的平均面积,其他以此类推,得到公式(1):
(1)
比例模型:在持续的高浓度差作用下,在菲克扩散基础上增加药物分子转移的速率,其与一般模型的区别在于药物分子较多的节点HE的值偏大,见公式(1)。
容量模型:在一定时间内限制药物分子在一个节点中的量,是对菲克扩散的扩展,需乘以容量系数y(x),当分子移动的目标节点远未达到饱和时,用公式(2)计算,当目标节点接近饱和时,以公式(3)计算,其中x表示两个节点之间分子转移的量,最后把得到的系数y代入公式(4)。
(2)
(3)
(4)
2.1.2 多孔扩散模型Mitragotri等[11]认为亲脂性小分子药物经细胞间质通路进入体内并不是单纯的扩散过程,需要通过曲折的空隙,并基于菲克扩散与定标粒子理论建立多孔扩散模型,得到公式5。Mitragotri等[11]使用Johnson[12]的脂溶性小分子药物数据库对模型进行线性回归,得到公式6,结果表明该模型预测结果较好,平均误差为5%,比Potts-Guy的溶解扩散模型误差小1.3%。
(5)
(6)
2.2 经细胞间隙与细胞内转运
2.2.1 两相模型Nitsche等[13]认为药物有两种途径透过角质层:细胞间隙通路与跨细胞通路,因此建立两相模型计算药物在含水角质层与载体之间的分配系数KSC/w(公式7),其中ølip表示细胞间隙脂质在角质层中的含量,øcor表示细胞在角质层中的含量,Klip/w表示药物在细胞间隙与载体之间的分配系数(公式8),Kcor/w表示药物在细胞与载体之间的分配系数(公式9),Ko/w表示药物在辛醇与水中的分配系数,PCpro/w表示药物在蛋白与水中的分配系数,ωpro表示蛋白质与无水角质层的质量比,υ表示水与无水角质层的质量比,ρwater与ρpro分别表示水与角蛋白的密度。Nitsche等[13]用72个水化的角质层数据进行线性回归,可得到最终公式(公式10),实验结果良好。
KSC/w=ølipKlip/w+øcorKcor/w
(7)
Klip/w=c(Ko/w)β
(8)
(9)
(10)
2.2.2 水泥砖块模型Chen等[14-15]基于角质层的形态学结构,结合机械原理、定标粒子理论与流体力学的阻碍扩散理论,把每个细胞与其周围的细胞间质划为一网格,得到了药物在两网格之间转移质量的计算公式(公式11),其中SAB表示两网格的接触面积,δ表示该网格的相对扩散长度,D表示该网格的扩散系数,PAB为药物在A、B网格的分配系数,C为该网格的浓度。Chen等[14-15]使用计算机模拟后,计算127个化合物的透皮系数,并与实测数据比较,预测结果较好(R2=0.74),比Potts-Guy模型[16](R2=0.52)与Mitragotri模型[11]好(R2=0.58)。
(11)
2.3 经角质层转运
2.3.1 溶解扩散模型 1990年,Flynn在相同的人体离体皮肤样本中测定97种化合物的吸收系数,这些数据表现出了吸收系数、化合物的亲油性与相对分子质量之间存在某种关系[17]。基于该数据库,Potts等[16]假设角质层为主要限速屏障,药物进入角质层后为被动稳态扩散,建立溶解扩散模型,得到公式12,最后使用Flynn的97个数据进行线性拟合,得到公式13,其中Kp表示透皮系数,Kow为辛醇-水分配系数,MW为相对分子质量,拟合效果良好(R2=0.67)。
(12)
logKP=0.711logKOW-0.0061MW-6.3
(13)

(14)
(15)
(16)
2.3.3 二维瞬态扩散模型 为了全面了解经皮给药后药物在角质层的分布情况,Simon等[20]基于菲克扩散提出了一个二维瞬态扩散模型(公式17),并假设药物层的浓度不变,且除了皮肤与毛细血管外,皮肤周围无其他物质交换。Simon等[20]通过拉普拉斯转换,代入已知的初始条件,得到微分方程的通解(公式18),并求得浓度与时间的一阶微分方程的解(公式19),其中x表示纵向扩散距离x1与角质层厚度ls的比值,y表示横向扩散距离x2与ls的比值,w=lsKcl/D(Kcl表示药物的消除系数,D表示药物的扩散系数)。
(17)

(18)
3 经角质层与活性表皮层转运模型
活性表皮层是指表皮层中的基底层、棘细胞层与颗粒层,均为活细胞组成,具有分裂增殖、新陈代谢的功能。药物经皮进入体内的主要屏障是角质层,其他层一般情况可以忽略,但当药物的脂溶性很强时,通过角质层的速率较快,而活性表皮层有较多水溶性物质,脂溶性药物透过较难,此时不能忽略活性表皮层对药物的屏障作用。
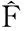
(20)
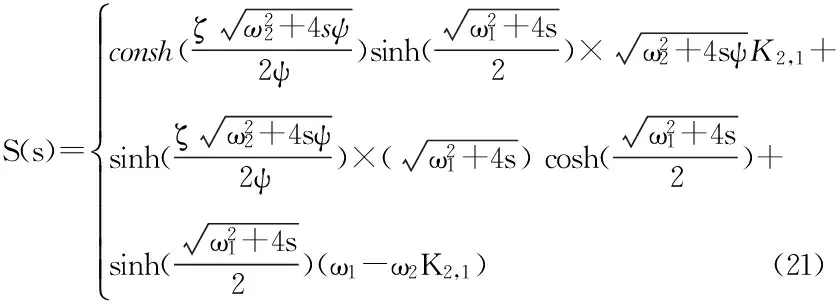
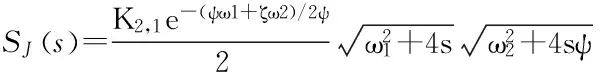
(22)
3.2 扩散/挥发瞬态模型Ray等[22-23]考虑药物的挥发作用以及角质层的向外推送对药物进入体内的影响,假设药物层、活性皮肤层皆为均质层,建立扩散/挥发瞬态模型,以质量守恒方程与菲克扩散第一定律计算药物从角质层到活性表皮层过程中浓度随时间变化的关系,得到公式23-24。
(23)
(24)
4 其他转运模型
药物进入体内的方式除了经角质层外,还可以经皮肤附属器进入真皮层,但不是主要通路,且特定情况下,活性表皮层和真皮层的屏障作用不能忽略。考虑到以上因素,部分文献报道了药物经这些途径进入体内的数学模型。
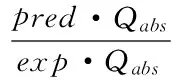
(25)
(26)
(27)
4.2 经皮肤附属器转运模型人体皮肤含有较多皮肤附属器,包括毛发、汗腺等,其毛囊总面积占人体皮肤中面积的0.1%,汗腺面积占0.01%[26]。对于分子量较大的亲水性药物,皮肤附属器是一条进入体内的重要通路[8,27]。Peck等[26,28]用多孔渗透模型计算药物经皮肤附属器进入体内的渗透系数(公式28),其中ε,τ与h分别表示皮肤的多孔性,路径曲折性与角质层的厚度,D是药物在载体中的扩散系数,λ表示药物分子的流体动力学半径。
(28)
4.3 经真皮转运药物进入充满毛细血管与毛细淋巴管的真皮层后,小分子的药物会通过毛细血管进入体循环,大分子的药物通过毛细淋巴管进入体循环,因此,经真皮转运的模型大多为消除模型[9]。根据前人的经验,Anissimov等[29]建立分布模型,描述药物在真皮层与皮下组织中血管与淋巴管对药物的摄取情况,并考虑血液流动、血蛋白吸附与真皮吸附对药物分布的影响,得到公式29,并分别用去羟米松(desoximetasone)、益康唑(econazole)、氢化可的松(hydrocortisone)、甲氧沙林(8-methoxypsoralen)、维甲酸(retinoicacid)、曲安奈德(triamcinoloneacetonide)在体内分布的实验数据进行线性回归,得到其确定系数(coefficientofdetermination)分别为0.54、0.84、0.91、0.94、0.33、0.39。
(29)
5 总结
本文介绍了多种预测药物经皮吸收的模型,这些模型大多是在扩散模型与室模型的基础上[2],采用菲克扩散理论、定标粒子理论、拉普拉斯转换的方法进行转换[9],最后通过有限差分法、直线法、有限元法、有限体积法、随机游动法等进行数值计算[30]。根据使用范围的不同,模型的着重点也有所不同,有些针对水溶性药物的经皮给药,有些针对脂溶性药物的经皮给药。
如今,数学模型建立时考虑的因素越来越多,如药物本身的性质、药物在皮肤中的吸附与解吸附、角质层本身的外排性、药物在皮肤转运的机制等。另外,模型的建立方法也越来越复杂,由原来的一维模型发展到二维甚至三维模型。除此之外,模型的类型也由原来Potts与Guy的稳态模型过渡到瞬态模型,研究的对象也由宏观向微观过渡,因此表达药物的吸收情况也由代数方程向微分方程过渡,更显复杂。
虽然药物经皮吸收的研究越来越多,但更多的是动力学方面的研究,一般使用微积分建立模型,且部分微积分方程无法得到精确解,只能通过计算机模拟的方式估算。此外,动力学研究所需的数据十分有限,同一皮肤样本所测数据稀少,数学模型能否准确预测还有待验证。而基于数据的定量构效关系研究(QSPR)由原来的简单的QSPR模型向基于机械理论的复杂模型过渡[5],但仍无重大突破,还有待发展。
从最近的研究趋势看,研究药物经皮转运的数学模型将有以下变化:(1)研究对象以经角质层转运的模型为主;(2)模型建立基于机械理论;(3)模型建立的范畴主要为三维微观模型;(4)模型的建立将主要考虑药物的扩散、吸附与代谢;(5)角化细胞将模拟为六角晶或间四边六角体(tetrakaidekahedral,TKD)。随着数学模型的不断优化,预测药物经皮吸收的结果将越准确,经皮给药途径将有助于经皮给药药物的研究。
[1]PrausnitzMR,MitragotriS,LangerR.Currentstatusandfuturepotentialoftransdermaldrugdelivery[J]. Nat Rev Drug Discov, 2004, 3(2):115-24.
[2]NaegelA,HeisigM,WittumG.Detailedmodelingofskinpenetration-Anoverview[J]. Adv Drug Deliv Rev, 2013, 65(2): 191-207.
[3]BhowmickM,SengodanT.Mechanisms,kineticsandmathematicalmodellingoftransdermalpermeation-anupdatedreview[J]. Int J Res Dev Pharm L Sci, 2013, 2(6): 636-41.
[4]VanGeleM,GeusensB,BrochezL,SpeeckaertR.Three-dimensionalskinmodelsastoolsfortransdermaldrugdelivery:challengesandlimitations[J]. Expert Opin Drug Deliv, 2011, 8(6): 705-20.
[5]ChenL,HanL,LianG.Recentadvancesinpredictingskinpermeabilityofhydrophilicsolutes[J]. Adv Drug Deliv Rev, 2013, 65(2): 295-305.
[6]CoutoA,FernandesR,CordeiroMN,etal.Dermicdiffusionandstratumcorneum:Astateoftheartreviewofmathematicalmodels[J]. J Control Release, 2014, 177(1): 74-83.
[7]JeppsOG,DancikY,AnissimovYG,RobertsMS.Modelingthehumanskinbarrier-towardsabetterunderstandingofdermalabsorption[J]. Adv Drug Deliv Rev, 2013, 65(2): 152-68.
[8]NorlénL.Thephysicalstructureoftheskinbarrier[M]//RobertsMS,WaltersKA. Dermal Absorption and Toxicity Assessment. Second Edition.England:CRCPress, 2007: 37-68.
[9]AnissimovYG,JeppsOG,DancikY,RobertsMS.Mathematicalandpharmacokineticmodellingofepidermalanddermaltransportprocesses[J]. Adv Drug Deliv Rev, 2013, 65(2): 169-90.
[10]SchummP,ScoglioCM,vanderMerweD.Anetworkmodelofsuccessivepartitioning-limitedsolutediffusionthroughthestratumcorneum[J]. J Theor Biol, 2010, 262(3): 471-7.
[11]MitragotriS.Atheoreticalanalysisofpermeationofsmallhydrophobicsolutesacrossthestratumcorneumbasedonscaledparticletheory[J]. J Pharm Sci, 2002, 91(3): 744-52.
[12]JohnsonME,BlankschteinD,LangerR.Evaluationofsolutepermeationthroughthestratumcorneumlateralbilayerdiffusionastheprimarytransportmechanism[J]. J Pharm Sci, 1997, 86(10):1162-72.
[13]NitscheJM,WangTF,KastingGB.Atwo-phaseanalysisofsolutepartitioningintothestratumcorneum[J]. J Pharm Sci, 2006, 95(3): 649-66.
[14]ChenL,LianG,HanL.Useof“bricksandmortar”modeltopredicttransdermalpermeation:modeldevelopmentandinitialvalidation[J]. Ind Eng Chem Res, 2008, 47(17): 6465-72.
[15]ChenL,LianG,HanL.Modelingtransdermalpermeation.PartI.Predictingskinpermeabilityofbothhydrophobicandhydrophilicsolutes[J]. AIChE J, 2010, 56(5): 1136-46.
[16]PottsRO,GuyRH.Predictingskinpermeability[J]. Pharm Res, 1992, 9(5): 663-9.
[17]MossGP,WilkinsonSC,SunY.Mathematicalmodellingofpercutaneousabsorption[J]. Curr Opin Colloid Interface Sci, 2012, 17(3): 166-72.
[18]AnissimovYG,RobertsMS.Diffusionmodellingofpercutaneousabsorptionkinetics: 4.Effectsofaslowequilibrationprocesswithinstratumcorneumonabsorptionanddesorptionkinetics[J]. J Pharm Sci, 2009, 98(2): 772-81.
[19]FraschHF,BarberoAM,HettickJM,NitscheJM.Tissuebindingaffectsthekineticsoftheophyllinediffusionthroughthestratumcorneumbarrierlayerofskin[J]. J Pharm Sci, 2011, 100(7): 2989-95.
[20]SimonL,OspinaJ.Two-dimensionaltransportanalysisoftransdermaldrugabsorptionwithanon-perfectsinkboundaryconditionattheskin-capillaryinterface[J]. Math Biosci, 2013, 244(1): 58-67.
[21]SimonL,GoyalA.Dynamicsandcontrolofpercutaneousdrugabsorptioninthepresenceofepidermalturnover[J]. J Pharm Sci, 2009, 98(1): 187-204.
[22]RayChaudhuriS,KastingGB,KrantzWB.Percutaneousabsorptionofvolatilesolventsfollowingtransientliquidexposures:I.Modeldevelopment[J]. Chem Eng Sci, 2009, 64(5): 1027-35.
[23]RayChaudhuriS,GajjarRM,KrantzWB,KastingGB.PercutaneousabsorptionofvolatilesolventsfollowingtransientliquidexposuresII.Ethanol[J]. Chem Eng Sci, 2009, 64(8): 1665-72.
[24]DancikY,MillerMA,JaworskaJ,KastingGB.Designandperformanceofaspreadsheet-basedmodelforestimatingbioavailabilityofchemicalsfromdermalexposure[J]. Adv Drug Deliv Rev, 2013, 65(2): 221-36.
[25]KastingGB,MillerMA,BhattVD.Aspreadsheet-basedmethodforestimatingtheskindispositionofvolatilecompounds:applicationtoN,N-diethyl-m-toluamide(DEET)[J]. J Occup Environ Hyg, 2008, 5(10): 633-44.
[26]MitragotriS,AnissimovYG,BungeAL,FraschHF.Mathematicalmodelsofskinpermeability:Anoverview[J]. Int J Pharm, 2011, 418(1): 115-29.
[27]MeidanVM,BonnerMC,MichniakBB.Transfolliculardrugdelivery—isitareality[J]? Int J Pharm, 2005, 306(1): 1-14.
[28]PeckKD,GhanemAH,HiguchiWI.Hindereddiffusionofpolarmoleculesthroughandeffectiveporeradiiestimatesofintactandethanoltreatedhumanepidermalmembrane[J]. Pharma Res, 1994, 11(9): 1306-14.
[29]AnissimovYG,RobertsMS.Modellingdermaldrugdistributionaftertopicalapplicationinhuman[J]. Pharm Res, 2011, 28(9): 2119-29.
[30]FraschHF,BarberoAM.Applicationofnumericalmethodsfordiffusion-basedmodelingofskinpermeation[J]. Adv Drug Deliv Rev, 2013, 65(2): 208-20.
Progress of mathematical modeling for trandermal drug absorption
HE Xing-yao, WANG Hui
(GuangdongPharmaceuticalUniversity,Guangzhou510006,China)
Transdermal drug delivery is an administration route which can avoid the first-pass effect, maintain steady plasma concentrations and enhance bioavailability. Drug transporting through the skin by passage through the stratum corneum leads to the viable epidermis and the dermis. With the development of the computer technology, many mathematical models for predicting the absorption of drugs have been built according to physical and chemical properties of drugs and physiological characteristics of each skin layer. This article presented provides a summary of the progress of mathematical models for predicting percutaneous absorption of drugs.
percutaneous absorption; transdermal absorption; prediction of percutaneous absorption; mathematical model; permeability coefficient;transdermal drug delivery; percutaneous transport
时间:2015-4-15 15:44 网络出版地址:http://www.cnki.net/kcms/detail/34.1086.R.20150415.1545.004.html
2014-12-15,
2015-01-18
国家自然科学基金资助项目(No 81072591);广东省科技计划项目(No 2012B060300030)
何星垚(1990-),男,硕士生,研究方向:皮肤药理学,E-mail:719660180@qq.com; 王 晖(1964-),男,教授,研究方向:皮肤药理学,通讯作者,Tel:020-39352880,E-mail:gdwanghui2006@126.com
10.3969/j.issn.1001-1978.2015.05.002
A
1001-1978(2015)05-0596-05
R-05;R322.99;R334.5;R452; R969.1

