基于空间谱插值的DOA估计算法*

陈 雨，王旭东，樊 涛

（南京航空航天大学电子信息工程学院，江苏南京210016）

基于空间谱插值的DOA估计算法*

陈 雨，王旭东，樊 涛

（南京航空航天大学电子信息工程学院，江苏南京210016）

现有的MUSIC、ESPRIT等基于特征值分解算法，在信号DOA估计时运算复杂度较高，不利于硬件实现，而经典空间FFT算法虽然运算速度快，但在天线数不甚多时，其较大的离散角度间隔限制了DOA估计精度。为此，提出了一种基于空间谱插值的DOA估计算法。该方法在经典空间FFT算法的基础上，对量化空间谱进行线性插值，只增加1次除法运算，不改变原有算法结构，利于硬件实现。当信噪比大于9dB时，其均方根误差接近克拉美-罗限（CRLB）。仿真实验证明了算法的精确度和有效性。

DOA估计；FFT空间谱；线性插值；CRLB

0 引言

利用阵列信号处理技术实现对远场信号的DOA估计，近年来一直是人们研究的热点，其在通信、雷达、电子侦察、水声信号处理等领域得到广泛应用。空间谱估计技术可实现对多目标测向，对阵元排列没有特殊要求，这给阵元及天线阵设计带来极大灵活性且其测向精度优于传统比幅、比相方法［1］。本文提出了一种基于FFT空间谱插值的DOA估计算法，该算法运算速度快，估计精度高于传统空间谱DOA算法，且算法结构规整，能够进行并行流水化数据处理。易于用FPGA等硬件实现。解决了MUSIC、ESPRIT等基于特征值分解的DOA估计算法难以硬件实现，不利工程应用的难题。本文对算法进行了详细分析和仿真验证，给出了在FPGA芯片内实现时的硬件设计框图。

1 算法分析

1.1 FFT空间谱DOA估计

间距为d的M个阵元排列成一个均匀线阵，假定一位于阵列远场的信号源，其波长为λ，传播速度为c，阵列方向与信号入射方向的夹角即DOA为θ1，如图1所示。

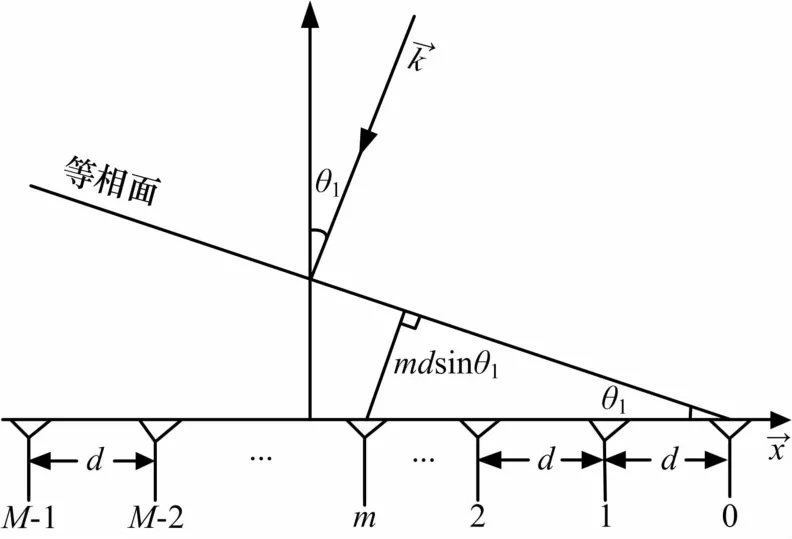
图1 平面波入射均匀线阵模型

设定最右边一个阵元为参考阵元，假定基带信号幅度不变，则第m个阵元的接收信号为：

式中，A、f分别表示接收信号的幅度和载波。为公式推导方便，令→k1为一个与波的传播方向相同的单位向量，→x是一个沿着阵列方向的单位向量，式（1）可以写为：

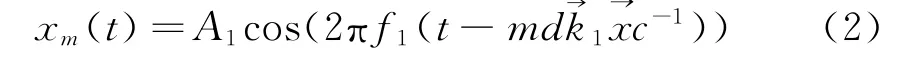
此处

因此，在t＝0时刻天线接收信号的复指数形式可表示为：

那么在空间域上的傅里叶变换为：

其模值为：

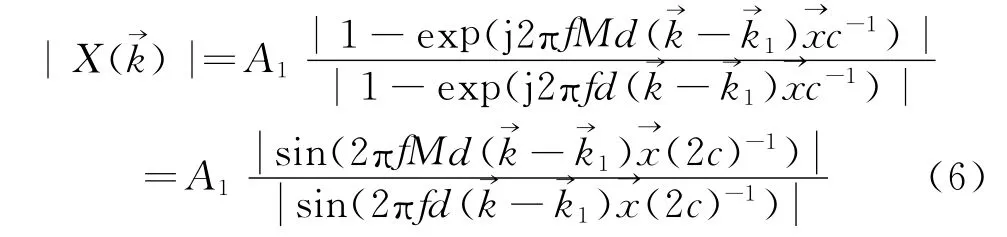
因（→k－→k1）→x＝－sin（Δθ），Δθ表示信号DOA矢量与第k根离散空间谱矢量的夹角。当→k＝→k1时，Δθ＝0，|X（→k）|达到峰值Max。即空间谱的峰出现在入射波方向上，据此可以估计出信号的波达方向。工程中一般采用快速傅里叶变换（FFT）来计算上述算法。

对M元均匀线阵，采用FFT算法可以至多形成M个独立的谱峰，且这些谱峰的相移量是等间距的，即：

第k个谱峰相对于第1个谱峰的相移量为：

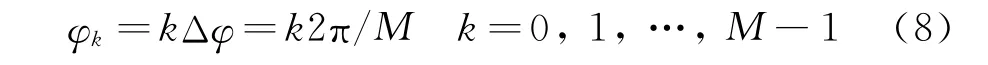
由式（5）知：

由此可得：

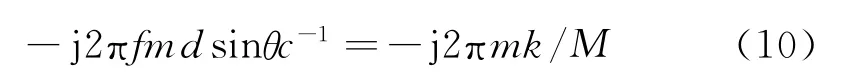
进一步推导可得：

即M个FFT空间谱峰与信号DOA的对应关系。

1.2 空间谱插值

根据FFT空间谱峰位置，进行DOA估计的方法，结构规整、便于实时处理。但由于FFT得到的是离散谱，谱线间隔限制了波达角估计精度。只有当信号波达角与量化FFT空间谱对应时，空间FFT法得到的DOA估计值才是准确的。当信号波达角与FFT的离散空间谱不重合时，信号的实际波达角位于两条谱线之间，与FFT量化空间谱对应的DOA值相差较大，算法的估计精度显著下降。本文通过对FFT运算后的空间谱线进行插值，可显著提高DOA估计精度。

由于Δθ较小，式（6）可以简化为：

考虑有限阵元空间傅里叶变换的加窗效应，由上式所描述的FFT空间谱，可以看成是对空间采样信号加入了宽度为M的矩形窗，M为阵元数。这种空间谱是离散的，且以辛格函数为轮廓，如图2所示。

图2中辛格函数的峰值位于Δθ＝0处，且第1个最小值出现在±1／M处。但是空间谱的最大分量与辛格函数的最大值并不一致。在这里各空间谱分量间隔是相同的，都相距1／M。假设X0表示空间谱分量的幅度最大值，X1表示次大值，X2表示第3大值。从图2可见，2个最大值位于主瓣，第3大值位于副瓣。根据这些空间谱分量可估计最大值的真实位置。

假设k是辛格函数峰值与X0之间的距离，则X1位于k－1／M处，它们相应的幅度为：

图2 M元均匀线阵空间谱包络

即：

从上述方程可以得到：

式（16）可以用来计算空间谱峰值位置。如果对应于X0和X1的空间谱位置分别为k0和k1，那么一旦求出k，就可以计算峰值位置：

带入式（11），即可得到FFT空间谱插值后的DOA估计值。当次大谱线位于左侧时，上式取负号，反之取正号。

为提高低信噪比时算法DOA估计性能，本文对FFT空间谱在时域按快拍数进行累加，然后再在空间谱进行插值，算法流程如图3所示。

图3 空间谱插值算法流程图

1.3 复杂度分析

MUSIC算法主要由构成信号的协方差矩阵、对协方差矩阵进行特征分解以构成噪声子空间、谱峰搜索三部分运算组成［2］。对于1个M元均匀线阵，当信号快拍数为N时，其复杂度分别为O（NM2）、O（M3）和O（M2）。因此，MUSIC算法的复杂度可记为O（NM2+M3+M2）。时域累加空间FFT算法进行DOA估计，需进行FFT运算、时域累加等运算［3］，共需NM／2log2M次复数乘法，以及NM log2M次复数加法。由于硬件实现时主要考虑乘法运算复杂性，因此，时域累加空间FFT算法的复杂度记为O（NM／2log2M）。本文提出的空间谱插值算法只要在空间FFT算法基础上，进行1次谱线插值运算，因此只增加1次除法运算，其复杂度为O（NM／2log2M+1）。

分析结果表明插值算法的复杂度要远小于MUSIC算法，与空间谱FFT算法相当。而对于各类改进的MUSIC算法［4-5］，主要集中在谱峰搜索时减少运算量，自相关矩阵计算、特征分解的计算量依然较大，所以此类算法计算量与MUSIC算法在同一量级。

由于算法运算复杂度低，且FFT和插值算法结构规整，能够进行流水线处理，因此，可以在FPGA芯片内实现这种并行DOA估计算法，其硬件实现如图4所示。

图4 插值算法的硬件实现框图

图4 中对天线接收的射频信号首先进行模拟下变频，在中频用ADC器件进行量化，然后对16路并行数据做FFT运算，得到空间谱。累加提高信噪比，谱线搜索加门限比较，可确定最大、次大谱线及信号个数，插值后得到DOA估计结果。

算法所需硬件资源有限，可在1片中等规模的FPGA芯片内得以实现，运算速度快，能够满足实时工程应用的需求。

2 仿真验证

仿真1：参数设置均匀线阵阵元数M＝16，基线波长比d／λ＝0.5，快拍数N＝512，高斯白噪声，信噪比为12 dB，信号的波达角设置为10°、40°、60°，分别采用FFT空间谱DOA估计方法、MUSIC算法和插值算法，得到的谱图如图5所示。

从图5可以看到，FFT空间谱DOA估计的谱图中3个谱峰对应的角度与信号的波达角有一定的偏差，而MUSIC算法与空间谱插值算法的谱图中谱峰对应的角度则比较接近，可以准确估计多信号的波达方向。但是插值算法的角度分辨率受到接收天线阵元数的限制，比MUSIC算法精度低。

为便于比较，这里给出均匀线阵DOA估计克拉美-罗限（CRLB）。由文献［6］知，当快拍数和阵元数较大时，DOA估计的CRLB为：

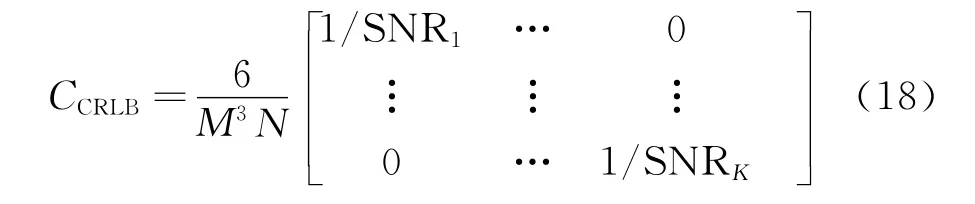
SNR i（i＝1，2，…，K）是第i个信号的信噪比，M、N分别为阵元数和快拍数。

仿真2：信号源为单信号，DOA设置为33°至44°，步进为0．1°，蒙特卡洛仿真次数为1000，其它参数设置与仿真1相同。

分别采用时域累加FFT空间谱DOA估计方法、MUSIC算法和插值算法，得到DOA估计均方根误差，并与CRLB进行比较，如图6所示。

图5 三种算法测向谱图比较

图6 算法在FFT量化空间谱区间内的性能

图6 中33．7°和44°是FFT量化空间谱对应的角度值。可以看出，当信号到达角位于FFT量化空间谱附近时，FFT法DOA估计误差很小，但是当DOA位于两根谱线中间区域时，估计误差很大。而插值算法在整个区域内的性能较平坦，量化点处误差稍大，绝大部分区域性能优越，接近CRLB。而MUSIC算法虽然性能最优，但是计算复杂，硬件实现难，限制了其在实时或准实时信号处理领域的应用。

仿真3：入射信号的信噪比为－10 dB到10 dB，步进为1 dB，信号入射角为38°，其它仿真条件不变，仿真结果如图7所示。

图7 算法性能比较

仿真结果表明，FFT空间谱插值DOA估计算法能明显改善单纯基于FFT量化空间谱的DOA估计算法，与MUSIC算法相当。当SNR≥9dB时，插值算法的DOA估计精度接近克拉美-罗限。

3 结束语

本文在分析原始FFT空间谱DOA估计算法基础上，通过对时域累加离散空间谱进行插值，可得到真实谱峰位置的高效估计，进而显著提高了算法性能。该算法只要在原始算法基础上，增加1次除法运算，不改变原有算法架构，因此可以充分利用FFT的高效运算结构，实现并行、流水线操作。仿真结果表明，算法在整个FFT量化空间谱区域内性能平稳，能有效克服FFT空间谱DOA估计算法在中心区域性能恶化问题，与MUSIC算法性能相当。可应用于雷达、电子侦察等对DOA估计实时性要求高的工程领域。■

［1］ 龚享铱，皇甫堪，袁俊泉．基于相位干涉仪阵列二次相位差的波达角估计算法研究［J］．电子学报，2005，33（3）：444－445．

［2］ Schmidt R．Multiple emitter location and signal parameter estimation［J］．IEEE Trans on Antennas＆Propagation，1986，34（3）：276－280．

［3］ Tsui J．Special design topics in digital wideband receivers［M］．Chapter 16，Nor wood，MA：Artech House，2010．

［4］ 计征宇，杨向华．基于FFT与MUSIC的改进DOA估计算法［J］．系统仿真学报，2010，22（2）：487－490．

［5］ 袁国靖，丁君，郭陈江．一种快速高分辨率的DOA估计方法——FFT-BMUSIC法［J］．微波学报，2005，21（1）：10－13．

［6］ Stoica P，Nehorai A．MUSIC，maximum likelihood，and Cramer-Rao Bound［J］．IEEE Trans on ASSP，1989，37（5）：720－741．

DOA estimation method based on spatial spectrum interpolation

Chen Yu，Wang Xudong，Fan Tao
（Department of Electronic and Information Engineering，Nanjing University of Aeronautics＆Astronautics，Nanjing 210016，Jiangsu，China）

Classical eigenvalue decomposition based signal DOA estimation method like MUSIC，ESPRIT are computation complex．These DOA estimation methods are not suit for hardware implementation．The conventional spatial FFT algorithm is faster，but the larger discrete angle interval restrict DOA estimate precision when the antenna number is not so many．Therefore，a novel DOA estimation method based on spatial spectrum interpolation is proposed．This method is based on the classical spatial FFT algorithm．Linear interpolation on the two maximum quantization spatial spectrums is used．Compared with the original algorithm，this method only adds a division operation．And，the algorithm structure is not modified．Thus，it is convenient for hardware implementation．When SNR exceed 9dB，the DOA estimation root mean-square error approach Cramer-Rao Low Bound（CRLB）．Accuracy and effectiveness of this DOA estimation method are verified by abundant simulation results．

DOA estimation；FFT spatial spectrum；linear interpolation；CRLB

TN971

A

国家自然科学基金（61201208）

2014-08-20；2015-03-10修回。

陈雨（1990－），女，硕士研究生，研究方向为信号处理。