基于MSP430系列微控制器的FFT算法实现

李小光

（西安航空学院 理学院，陕西 西安 710077）

随着各种电力电子装置在电力系统越来越广泛的应用，其非线性的特点使得供电中的谐波失真问题日益严重。监测技术的研究对市电质量的补偿具有很高的价值，考虑到实际情况，在供电系统质量监测中需要一些低成本，但分析速度较快的监测系统。

离散时间采样的快速傅里叶变换FFT （fast Fourier transform）算法是目前最主要的谐波检测和分析方法。FFT算法的实现可以采用专用芯片[1]37－40、DSP 芯片[2]6－11[3]41－44、FPGA芯片[4]193－207以及微控制器等。随着集成电路制造技术和数字计算机技术的进步，微控制器芯片的功能和所能提供的逻辑资源越来越多。MSP430F1611微控制器芯片属于TI公司 MSP430x1xx系列产品中的一种[5－6]，该芯片具有10240字节的 SRAM（Static Random Access Memory）存储器、48 k 字节的程序存储器、8通道 12位 ADC、2通道 12位 DAC、16位×16位硬件乘法器模块等片内资源。硬件乘法器模块支持8/16位×8/16位有符号，或者无符号的乘法运算，并可以选择“乘法与累加”功能。采用MSP430系列微控制器实现FFT算法具有超低功耗、低电压工作、低成本、分析速度快等优点，它比采用专用芯片和DSP芯片价格便宜，比采用FPGA芯片容易实现。

1 利用微控制器实现FFT算法

快速傅里叶变换在信号处理中的线性滤、相关计算、谱分析等方面起着重要的作用。将N点采样数据分解为更短的数据段来进行计算可以提高计算效率，目前使用最广泛的是基2的FFT算法。图1给出基2按时间抽取的快速傅里叶变换中的基本运算过程[5]379－388[6]181－189。

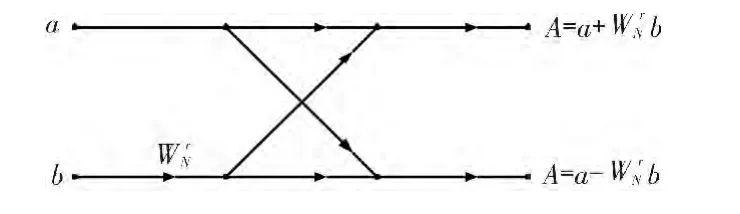
图1 基2按时间抽取的快速傅里叶变换中的基本运算Fig.1 Base 2 extraction according to time the basic operation of the fast Fourier transform

这种运算过程被称为蝶形运算，因为它的流程图看起来就像一个蝴蝶。每次蝶形运算包括一次复数乘法运算和两次复数加法运算。一旦对一对复数（a，b）执行了产生（A，B）的蝶形运算，原数据就无须再保存，所以可以将结果（A，B）保存在与数据（a，b）相同的数据存储单元。

由于MSP430系列微控制器的开发软件不支持复数运算[7]，这里复数运算需要分解成实部和虚部分别来完成，下面的函数“fft_2sin”用来实现蝶形运算。

2 利用查表代替相位因子中的三角函数运算

图2给出8点数据的基2按时间抽取的快速傅里叶变换流程图。整个数据分析需要多个阶段才能完成，每个阶段需要多次调用基2的FFT算法函数。在前面给出的函数“fft_2sin”中需要通过三角运算分别完成相位因子实部和虚部的计算。三角函数计算需要花费大量的时间，但是在分析的数据点数量给定以后可以首先完成相位因子的计算，将计算值存储在一个数据表中，通过查表的方法代替三角函数计算。修改后的基2的FFT算法函数如下。

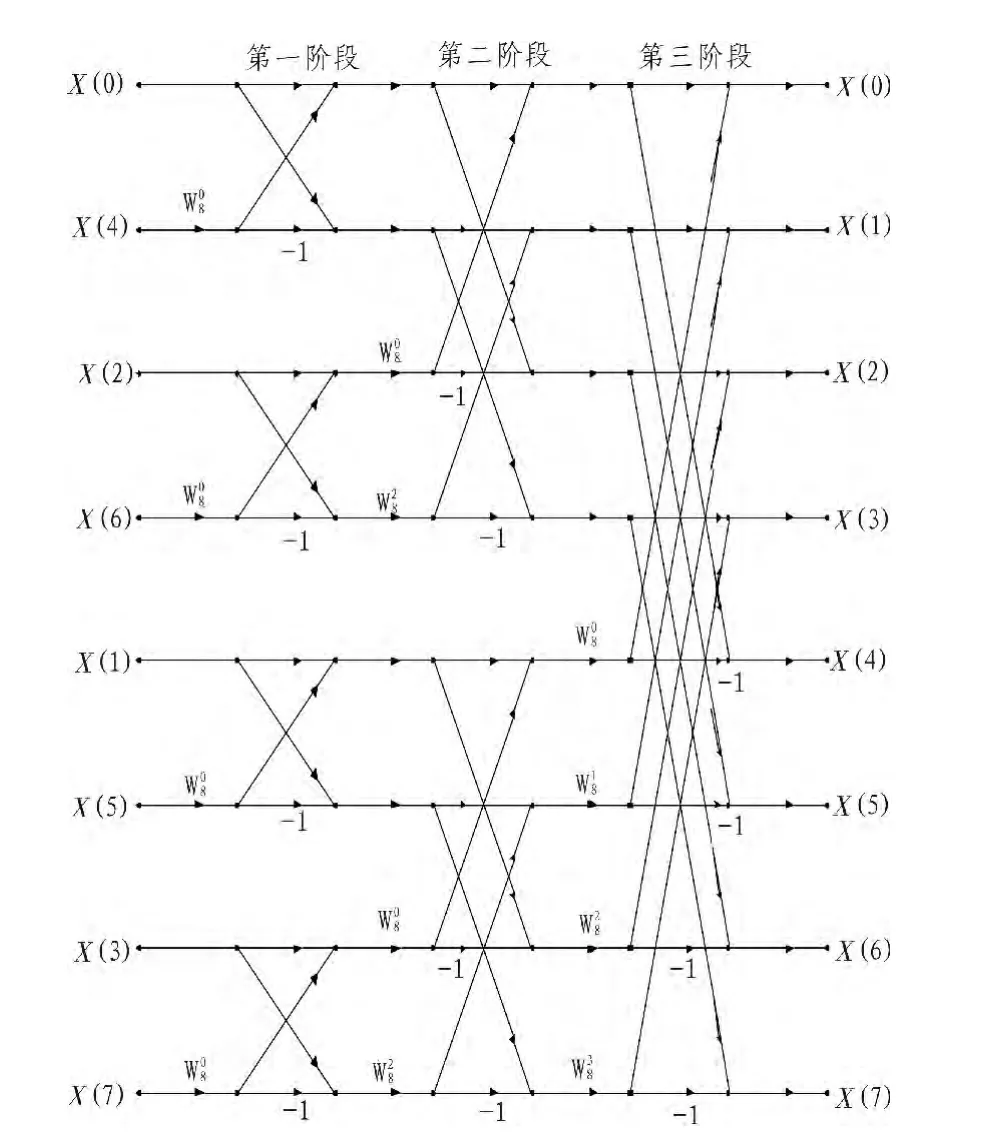
图2 8点数据的基2按时间抽取的快速傅里叶变换流程图Fig.2 8 data base 2 according to the time of extraction flow chart of fast Fourier transform

使用MSP430系列微控制器的开发软件IAR模拟显示，在基2的FFT算法函数中计算相位因子的情况下，完成一次函数计算需要花费7422时钟周期；利用查表获得相位因子的情况下，完成一次函数计算只需要花费1242时钟周期。

3 使用硬件乘法器进一步加快运算速度

完成采样数据的FFT分析的过程中需要进行大量的乘法运算，像其它的微控制器一样，MSP430系列芯片也是通过调用内部函数完成这些乘法运算的。利用硬件的方法完成要求的工作比使用软件模拟的方法快，也就是比利用编程实现的方法要快，但是添加硬件电路也将占用更多的逻辑资源。

TI公司在MSP430系列中的部分芯片中添加了硬件乘法器，利用开发软件中的编译选项可以方便地使用硬件乘法器代替内部函数来实现乘法运算。以完成图2给出8点数据的基2按时间抽取的快速傅里叶变换流程图为例，过程包括从采样数据的倒序排列，3个阶段基2的FFT计算，最终给出频谱分量的幅度数值。不使用硬件乘法器需要46592时钟周期，使用硬件乘法器需要41183时钟周期。

4 结 论

使用MSP430F1611微控制器芯片完成一个信号周期256个采样点的FFT分析，当被分析信号为50%占空比的方波，变换频率分量为 0，1，2，3时，方波信号频谱实际测量值分别为 127.500，162.342，0，54.1250，理论上的计算值分别为127.500，162.338，0，54.1127。 分析上诉结果可以得到实际测量值与理论计算值之间的绝对误差分别为0，0.004，0，0.012 3，相对误差为 0，0.002 5，0，0.023。

由上面的结论可以看出，利用程序产生256个采样数据，低电平数据为0，高电平数据为255，整个模拟程序占用芯片程序存储器3 492字节，数据存储器3 156字节。完成一次分析需要2 410 975时钟周期，当采用8 MHz的时钟信号需要约0.3 s，前10次谐波的计算相对误差低于千分之一。

TI公司新推出的MSP430F5xx系列产品的指令执行速度达到25MIPS，并提供32位×32位硬件乘法器模块[8]，这将进一步提高运算速度。

[1]孙国栋，雷在拴，周玉国，等.综合电力监控仪表的设计[J].电测与仪表，2007，44（7）:37-40.SUN Guo-dong，LEI Zai-shuan，ZHOU Yu-guo，et al.The design of the integrated power monitoring instrument[J].Electric Measurement and Instrument，2007，44（7）:37-40.

[2]任明炜，韩雪冰.基于TMS320F2812的混合型动态无功补偿控制系统的数字化实现[J].电测与仪表，2007，44（7）:6-11.REN Ming-hui，HAN Xue-bing.The hybrid dynamic reactive power compensation control system based on TMS320F2812 digital implementation[J].Electric Measurement and Instrument，2007，44（7）:6-11.

[3]周军，李志霞，陆勇.基于DSP的电能质量在线监测系统的研制[J].电测与仪表，2007，44（7）:41-44.ZHOU Jun，LI Zhi-xia，LIU Yong.Power quality online monitoring system based on DSP development[J].Electric Measurement and Instrument，2007，44（7）:41-44.

[4]Uwe Meyer-Baese著.刘凌，胡永生译.数字信号处理的FPGA实现[M].北京：清华大学出版社，2003.

[5]John G.Proakis，Dimitris G.Manolakis.数字信号处理[M].方艳梅，刘永清，等译.北京：电子工业出版社，2007：379-388.

[6]Steven W.Smith.实用数字信号处理——从原理到应用[M].张瑞峰，詹敏晶，等译.北京：人民邮电出版社，2010:181-189.

[7]IAR Embedded Workbench Version 3+for MSP430?User Guide[EB/OL].（2011-11-28）.[2012-2-10]http://www.ti.com/litv/pdf/slau138x.pdf.

[8]MSP430x5xx/MSP430x6xx Family User’s Guide［EB/OL］.（2011-12-19）. [2012-2-10]http://www.ti.com/litv/pdf/slau208j.pdf.