基于氢钟组的AT1及其改进原子时算法研究*

吴文娟 朱江淼 高 源 宋文峰

(1.北京工业大学电子信息与控制工程学院，北京 100124；2.中国计量科学研究院，北京 100029)



基于氢钟组的AT1及其改进原子时算法研究*

吴文娟1朱江淼1高 源2宋文峰1

(1.北京工业大学电子信息与控制工程学院，北京 100124；2.中国计量科学研究院，北京 100029)

本文针对中国计量科学研究院守时实验室内的氢钟组，研究基于氢钟组的AT1原子时算法，并对该算法进行一定程度的改进,并给出了这两种基于氢钟组的原子时算法的基本原理，流程图。然后，根据守时实验室测得的氢钟差数据，分别对这两种算法进行数据处理得到氢钟组的时间尺度。结果表明，由这两种原子时算法计算得到的钟组时间尺度的频率稳定度高于单台氢钟的频率稳定度，并且改进AT1原子时算法的实验结果更优，达到了预期的要求。

氢钟组；AT1算法；改进AT1算法；频率稳定度

0 引言

每台原子钟都可以维持一个时间尺度，但是，为了避免一台原子钟出现故障而影响时间尺度，守时实验室都使用多台原子钟组成一个钟组来守时。这样，就要求由各个原子钟的时间计算出标准时间，这就是原子时算法。原子时算法的优化程度及选用对原子时标的稳定度有着很大的影响[1]。

氢钟和铯钟的最大区别在于氢钟有很明显的频率漂移，而铯钟的频率漂极小，可忽略不计[2]。经典的AT1原子时算法中直接设定了频率漂移为零，而对于氢钟组频率漂移是需要考虑的，所以，这在一定程度上影响了AT1算法的处理结果。因此，本文对基于氢钟组的AT1原子时算法进行了研究，并尝试对该算法进行一定程度的改进。

1 基于氢钟组的AT1原子时算法

令xi(t),yi(t)分别表示第i台原子钟在t时刻的时差值与频率值，t 表示测量的时间间隔。对于基于铯钟组的AT1原子时算法即传统的AT1原子时算法，t+t 时刻的第i台原子钟的时差值可以根据式(1)进行估算[3]：

(1)

本文研究基于氢钟的原子时算法，氢钟与铯钟的最大区别在于氢钟具有频漂。所以，在基于氢钟的AT1原子时算法中，t+t 时刻的第i台原子钟的时差值不能根据式(1)来估计，需要在式(1)的基础上引入频漂量zi(t)，得到基于氢钟的时差估计式[4]，如式(2)所示：

(2)

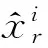
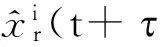
(3)

其中xri(t+t )表示第i台钟与参考钟之间的钟差。联立式(2)和式(3)可以得到式(4)：

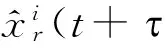
xri(t+t )

(4)

若氢钟组中有N台氢钟，那么上式可以重复N-1次，得到N-1个独立的估算值。最终的参考钟与组合钟之间的时差值是由这些估算值加权平均得到，如式(5)所示：

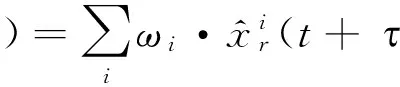
(5)

同时可以得到当前时刻第i台钟与组合钟之间的时差计算值xi(t+t )见式(6)：

xi(t+t )=xr(t+t )+xri(t+t )

(6)

在AT1原子时算法中，权重ωi是根据每台钟相对组合钟的预期值和当前计算值之差来确定。

2 基于氢钟组的改进AT1原子时算法

2.1 基于氢钟组的改进AT1原子时算法模型

由氢钟模型可以得到第i台钟的时差估算公式如式(7)所示[5]：

(7)

将式(7)两端同时加上钟差(设氢钟组中1号钟为参考钟)x1i(t)，可以得到式(8)：

(8)

假设有N组测量数据，也就是说有N组x1i，分别是{x1i1,x1i2,…,x1iN-1,x1iN}，对应的测量时间为{t1,t2,…,tN-1,tN}。钟差值与测量时间之间的数学关系如式(9)所示。

X=R·V+E

(9)

其中

(10)

根据最小二乘法可以得到R的最优估计如式(11)所示[6]：

(11)

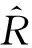
若选取第一台钟为参考钟，则氢钟组的时间尺度可以表示为：

(12)

因为当前时刻第i钟的时差是不可知的，所以，式(12)无法计算出钟组时间。但是因钟差值是可测的，所以可以对上式进行校正，如式(13)、式(14)所示：

(13)

(14)

其中，x1i(t)表示当前时刻第i台钟与参考钟之间的测量钟差；ωi是第i台钟的权重。下面具体介绍本部分确定权重ωi的方法。

2.2 基于SVM的权重确定方法

按照优化钟组时间的稳定度的思想，每台钟都将根据它的稳定度优劣来给定它的权重。因此，可以设定氢钟组中每台钟的权重反比于钟差的实际值与预测值的差，如式(15)所示：

(15)

x1i是测量值具有实时性，所以，需要提前预测当前时刻的钟差值来做比较。在本文中，选用支持向量机算法(SVM)进行预测。

SVM的基本思想是首先通过内积函数定义的非线性变换将输入空间变换到一个高维空间，然后，在高维空间中确定输入变量和输出变量之间的非线性关系[7]。设给定的训练集为：

{[x1i(t0),y1i(t0)],[x1i(t0+t ),y1i(t0+t )],…

[x1i(t0+m·t ),y1i(t0+m·t )]}

其中y1i表示频差，x1i,y1i∈R。支持向量机的拟合函数为：

y=f(x)=ω·φ(x)+b

(16)

其中，ω表示权重；b表示偏差；φ(·)是非线性映射函数，它可以用核函数代替。为了确定式(16)的平坦，必须找出最小的ω。这个问题可以表示为凸优化问题即：

(17)

约束条件为：

(18)

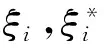
(19)

其中c是个正常数，其值越大数据的拟合程度越高。最后，通过引入拉格朗日乘子，式(19)转换为：

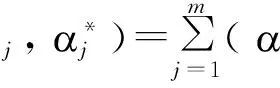
j·t )]+b

(20)

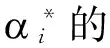
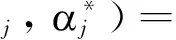
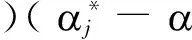
ak)K[x1i(t0+j·t ),x1i(t0+k·t )]

(21)

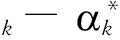
b= average{δk+y1i(t+k·t )-

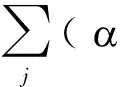
x1i(t0+k·t )]}

(22)

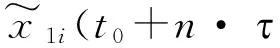
(23)

训练支持向量机的回归函数为：

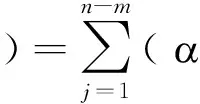
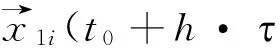
(24)

得到第一步预测[8]：

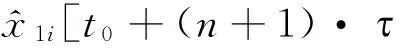
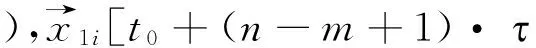
(25)

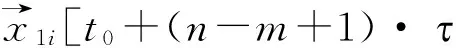
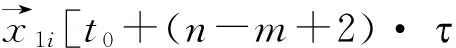
(26)

以此类推，可以得到第l步预测：

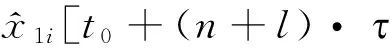
K{x1i(t0+j·t ),

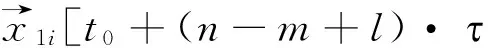
(27)

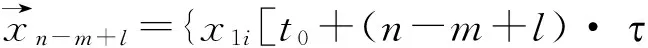
本文选用了守时实验室内钟差数据进行预测，并与传统的二元线性回归预测的结果进行了比较。预测结果表明支持向量机算法的预测准确度优于二元线性回归算法，更适用于钟差数据的预测。

3 实验数据处理

本文选取了守时实验室内的5台氢钟(其中1号为参考钟,其他分别是3号、4号、6号、7号)，对2013年11月到2014年3月之间测量的4组氢钟钟差数据(如图1所示)进行算法验证。最终通过两种原子时算法得到氢钟组的时间尺度如图2、图3所示。本文选用哈德曼方差来计算这五组数据的频率稳定度，结果如图4所示。从中可以看出氢钟组的时间尺度的稳定度优于单个氢钟，并且改进AT1原子时算法的结果优于传统的AT1原子时算法。

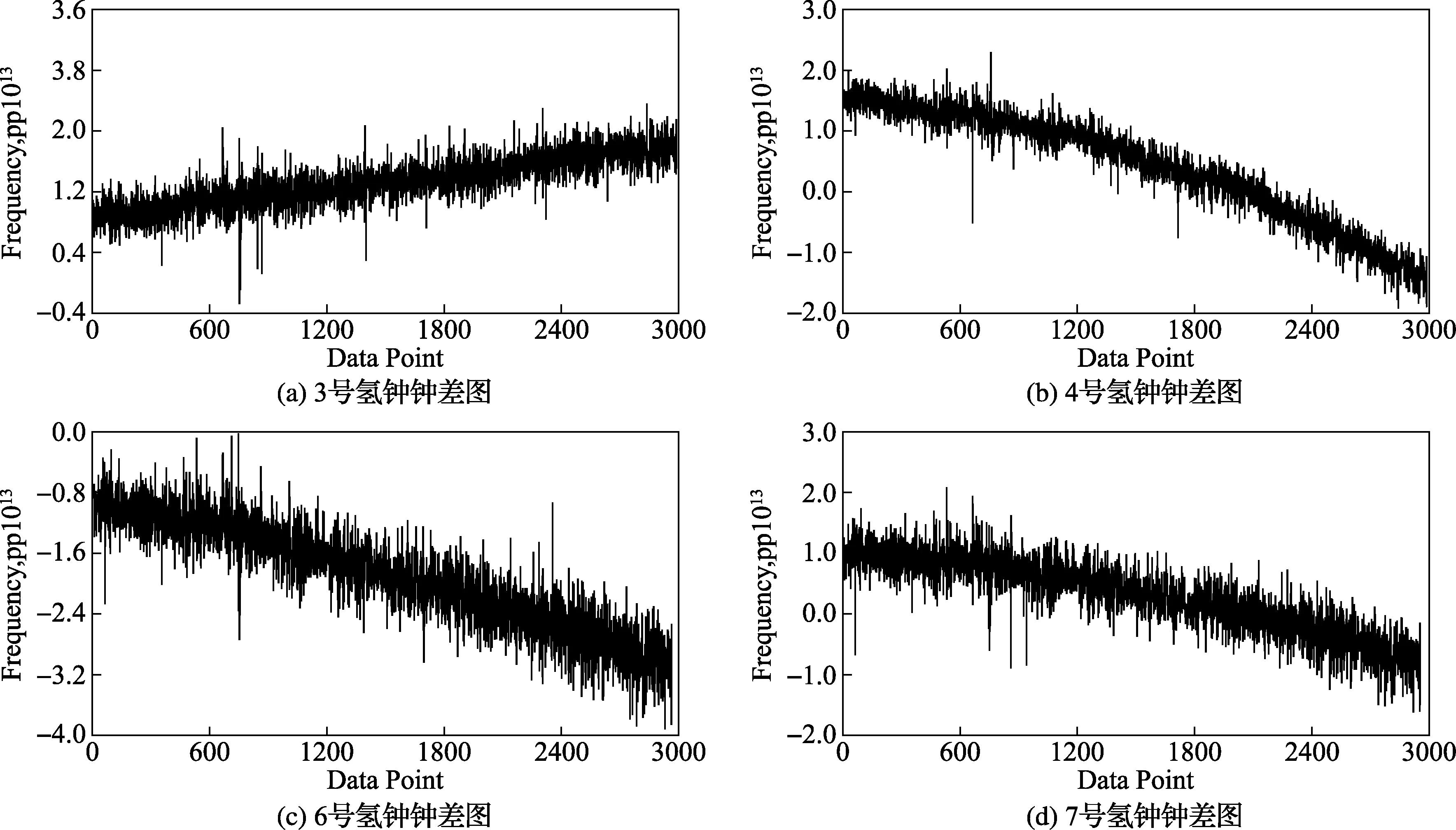
图1 氢钟钟差数据

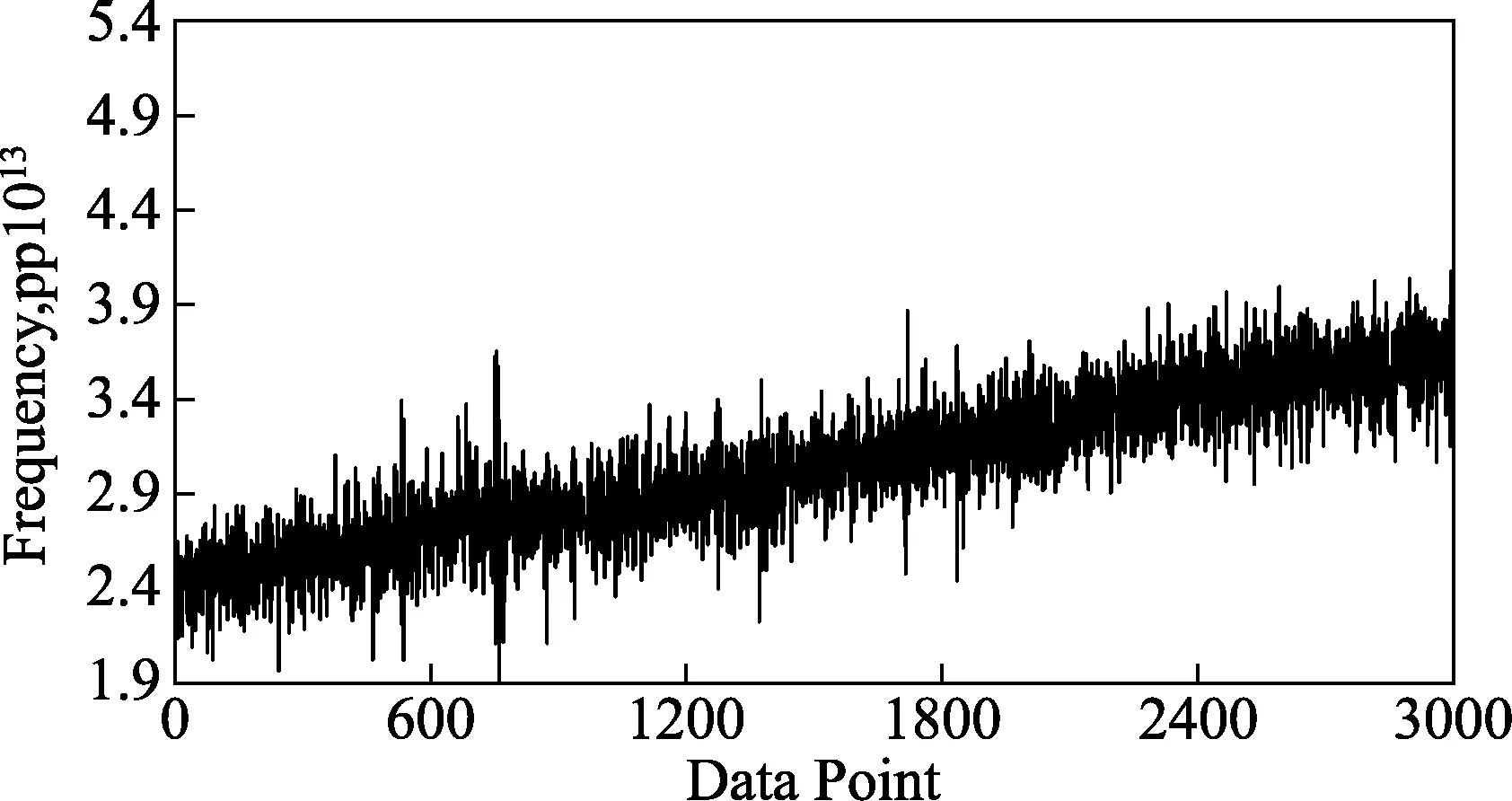
图2 基于氢钟组AT1原子时算法实验结果

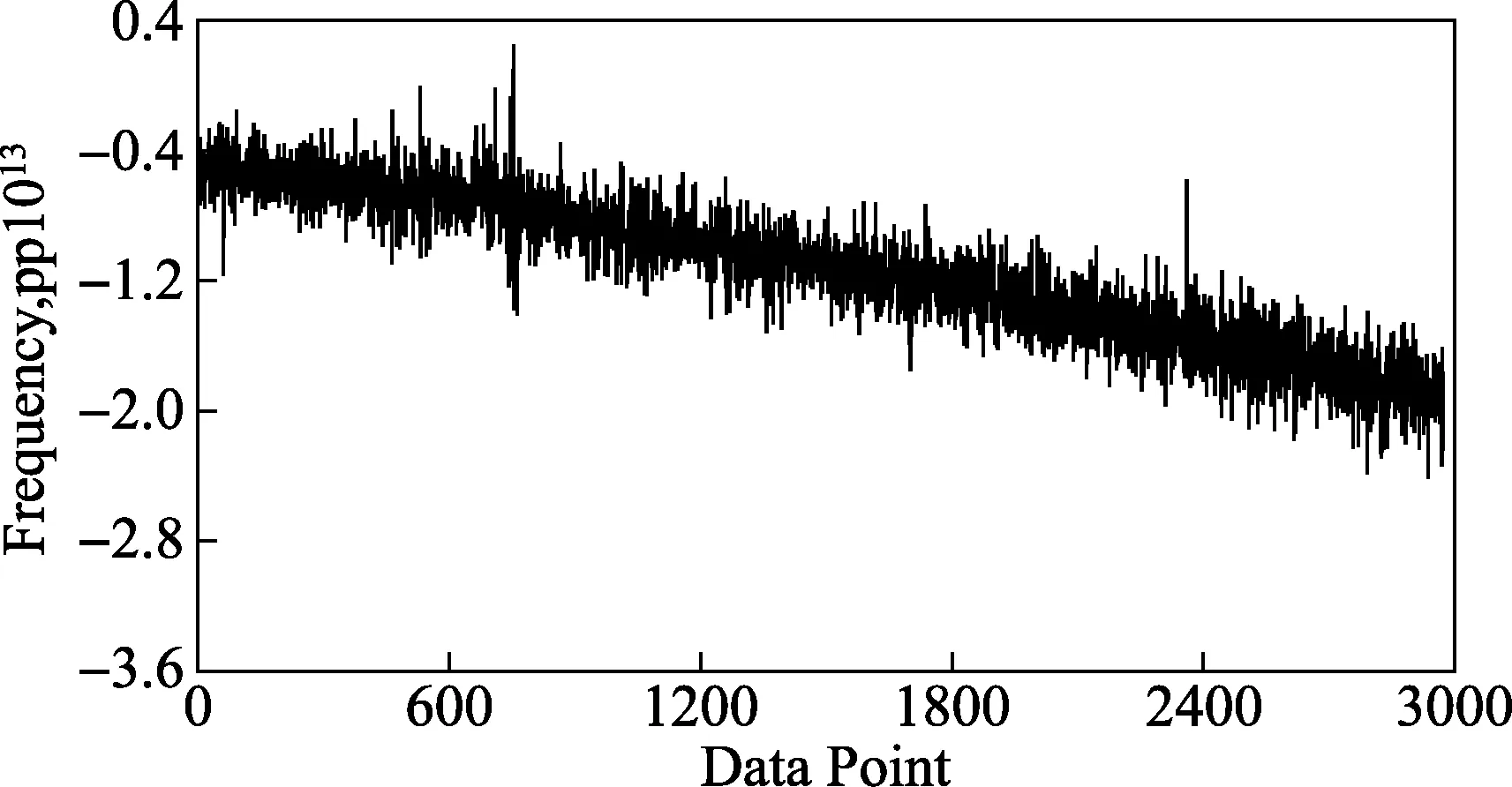
图3 基于氢钟组改进AT1原子时算法实验结果

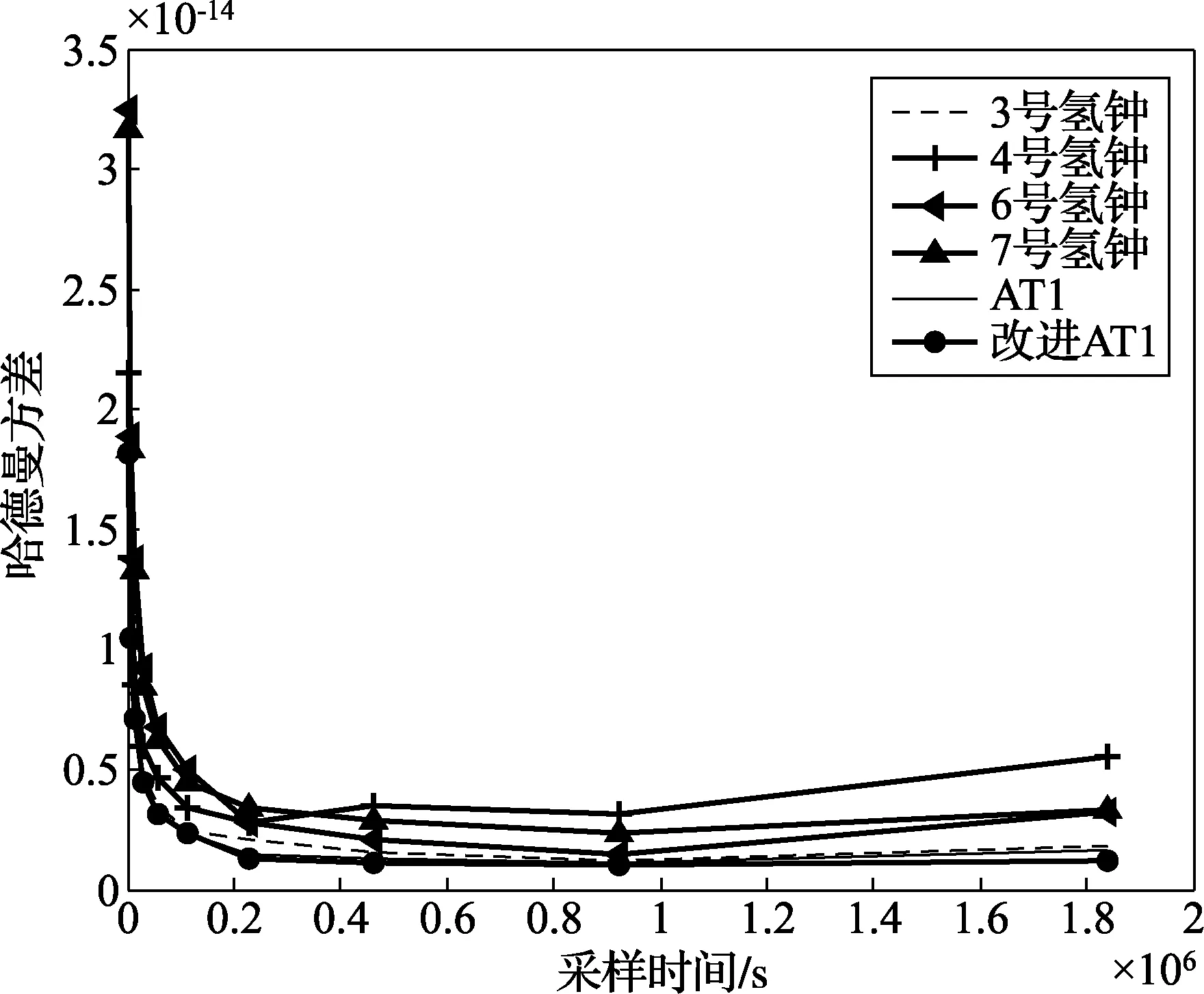
图4 频率稳定度

4 结论

本文研究了基于中国计量科学研究院守时实验室的氢钟组的AT1原子时算法及基于SVM改进AT1算法，并根据实际测量的钟差数据，通过上述两种算法分别得到了对应的氢钟组时间尺度和频率稳定度。氢钟组频率稳定度优于单台氢钟的稳定度，并且改进AT1原子时算法的稳定度高于AT1原子时算法，达到了本文的预期目标。

[1] TAKAOM.Definitions of Time andFrequency Standard[J].Journal of the National Institute of Information and Communications Technology，2003，50(2)

[2] 屈俐俐.氢钟守时应用.时间频率学报，2012，35(2)

[3] 张莉莉，高源.AT1原子时算法的研究.电子测量技术，2007，30(11)[4] Barnes J A, Jones R H, Tryon P V and Allan D W, Stochastic models for atomic clocks Proc.14th Annual PreciseTime and Time Interval (PTTI) Application and Planning Meeting，1982

[5] A.Cernigliaro and I.Sesia, INRIM Tool for Satellite Clock Characterization: Frequency Drift Estimation and Removal，MAPAN-Journal of Metrology Society of India (March 2012) 27(1)

[6] S.Weisberg, Applied Linear Regression，Wiley，New York(2005)

[7] 张娟，孙剑.基于SVM的城市快速路行程时间预测研究.交通运输系统工程与信息，2011，11(2)

[8] 尉询楷，李应红.基于支持向量机的时间序列预测模型分析与应用.系统工程与电子技术，2005，27(3)

科技部基础平台项目(2005DKA10703)

10.3969/j.issn.1000-0771.2015.3.01