柱帽的结构形式对无梁楼盖体系的成本影响

周 炜

(方兴地产(中国)有限公司，北京 100045)

柱帽的结构形式对无梁楼盖体系的成本影响

周 炜

(方兴地产(中国)有限公司，北京 100045)

以某地库工程项目为例，通过对“无梁楼盖”结构体系中柱帽的受力分析，指出在适当调整柱帽结构形式后能够使柱帽受力更为合理，并且整个无梁楼盖结构体系具有明显的经济优势。

无梁楼盖，柱帽，刚性角，冲切计算，弯矩

1 项目概述

某地库采用无梁楼盖结构体系。混凝土C40，顶板覆土2.0 m，柱网8.1 m×8.1 m，柱子600×600，层高3.6 m。地库顶板厚450，柱帽采用平托板形式，托板厚350，柱帽为2.7 m×2.7 m。

2 “平托板柱帽”结构形式的相关计算

2.1 荷载统计

地库顶板处场地活载q活=10.0 kN/m2，覆土q1=18×2=36.0 kN/m2，车库内电气设备管线以及板底抹灰等q2=4.0 kN/m2，车库顶板自重q3=25×0.45=11.25 kN/m2。荷载统计结果(恒载起主要控制作用)：

q设=1.35×(q1+q2+q3)+1.4×0.7×1.0×q活=78.99 kN/m2。

2.2 冲切计算

依据GB 50010—2010混凝土结构设计规范(以下简称“混凝土规”)6.5.1条之规定，取柱网中的“中柱”为研究对象，计算及图示如图1所示。

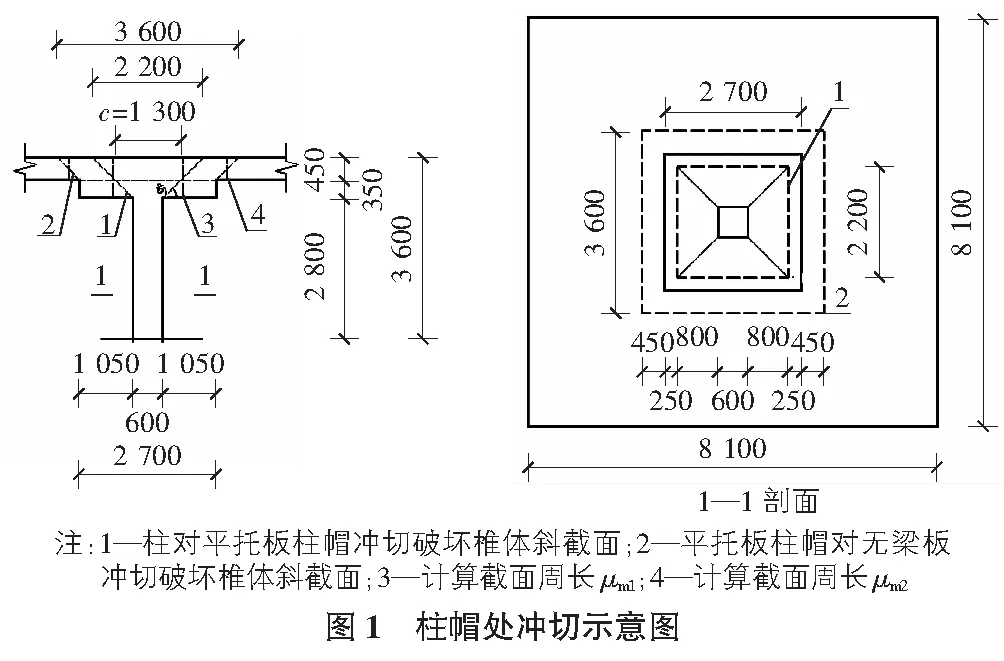
2.2.1 柱子对柱帽的冲切计算

计算参数：h01=450+350-40=760 mm；βh=1.0；ft=1.71 N/mm2；βs=2.0；中柱αs=40；μm1=(600+2×0.5×h01)×4=5 440 mm；η取η1和η2中的较小值，其中η1=0.4+1.2/βs=1.0，η2=0.5+(αs×h01)/(4×μm1)=1.90。

局部荷载设计值Fl=8.12×q设-(0.6+2×0.76)2×q设=4 827.52 kN。

截面抗冲切承载力[F]=0.7×βh×ft×η×μm1×h01=4 948.88 kN。

[F]/Fl=4 948.88/4 827.52=1.03>1，截面抗冲切满足要求。

2.2.2 平托板柱帽对无梁板的冲切计算

计算参数推导参考2.2.1，其中,h02=410 mm；μm2=12 440 mm；η=0.83。

局部荷载设计值Fl=8.12×q设-(2.7+2×0.41)2×q设=4 203.82 kN。

截面抗冲切承载力[F]=0.7×βh×ft×η×μm2×h02=5 067.30 kN。

[F]/Fl=5 067.30/4 203.82=1.21>1，截面抗冲切满足要求。

2.3 经验系数法求弯矩

2.3.1 经验系数法适用条件

无梁楼板在竖向均布荷载作用下，当符合下列条件时，其内力的计算可采用经验系数法：1)每个方向至少有三个连续跨；2)任一区格内的长边与短边之比不大于2；3)同一方向上的相邻跨度不相同时，大跨与小跨之比不大于1.2；4)活荷载与恒荷载之比应不大于3[1]。

该地库满足经验系数法适用条件，计算如下：

x方向总弯矩设计值：

M0=0.125×q设×Ly(Lx-2×c/3)2

(1)

y方向总弯矩设计值：

M0=0.125×q设×Lx(Ly-2×c/3)2

(2)

由于本项目柱网为8.1 m×8.1 m矩形柱网，即L=Lx=Ly=8.1 m，因此式(1)和式(2)可改写如下：

M0=0.125×q设×L(L-2×c/3)2

(3)

柱上板带弯矩设计值：

Mc=β1M0

(4)

跨中板带弯矩设计值：

Mm=β2M0

(5)

其中，q设为板的竖向均布荷载设计值；c为柱帽在计算弯矩方向的有效宽度(见图1)；β1,β2分别为柱上板带和跨中板带弯矩系数。

表1 弯矩系数

2.3.2 利用经验系数法计算弯矩

依据式(3)可得：

M0=0.125×q设×L(L-2×c/3)2=4 184.50 kN·m。

将表1中弯矩系数β1,β2分别代入式(4),式(5)后可得到内跨在支座和跨中处的弯矩设计值，如表2所示。

2.4 问题的提出

从对式(1)～式(3)的分析中发现，当柱网尺寸、柱帽尺寸以及荷载一定时，总弯矩M0只与变量c有关，即M0随着c值的增大而减小。而c值又与柱帽的结构形式有关，因此通过对柱帽结构形式的合理调整可以有效地增大c，而使得M0减小。

表2 弯矩设计值(一) kN·m

3 合理改变柱帽结构形式

3.1 刚性角及车库净高

混凝土结构的刚性角为45°。并且“混凝土规”6.5.1条有关板的受冲切承载力计算中，局部荷载或集中反力对板进行冲切破坏时，冲切破坏椎体斜截面与板面呈45°。如图2所示，即柱a对无梁板及平托板柱帽的冲切等效于柱b的冲切效果。

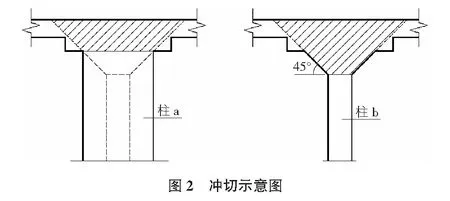
依据JGJ 100—98汽车库建筑设计规范4.1.13条，普通民用地下车库，对于微型及小型汽车而言，汽车库室内最小净高为2.2 m。

3.2 平托板+斜柱帽

在考虑民用建筑地下车库室内最小净高的前提下，将“平托板无梁楼盖”改成“平托板+斜柱帽无梁楼盖”的结构形式，可有效地增大柱帽的有效宽度c，如图3所示。

4 关于“平托板+斜柱帽”结构形式的相关计算

4.1 斜柱帽对平托板的冲切计算

计算参数推导参考2.2.1，其中：h01=760 mm；μm1=10 240 mm；η=1.0。

局部荷载设计值Fl=8.12×q设-(1.8+2×0.76)2×q设=4 311.87 kN。

截面抗冲切承载力[F]=0.7×βh×ft×η×μm1×h01=9 315.53 kN。

[F]/Fl=9 315.53/4 311.87=2.16>1，截面抗冲切满足要求。

4.2 平托板柱帽对无梁板的冲切计算

计算参数推导参考2.2.1，其中,h02=410 mm；μm2=12 440 mm；η=0.83。

局部荷载设计值Fl=8.12×q设-(2.7+2×0.41)2×q设=4 203.82 kN。

截面抗冲切承载力[F]=0.7×βh×ft×η×μm2×h02=5 067.30 kN。

[F]/Fl=5 067.30/4 203.82=1.21>1，截面抗冲切满足要求。

4.3 经验系数法求弯矩

依据式(3)可得：

M0=0.125×q设×L(L-2×c/3)2=3 310.09 kN·m。

将表1中弯矩系数β1,β2分别代入式(4)，式(5)后可得到内跨在支座和跨中处的弯矩设计值，见表3。

表3 弯矩设计值(二) kN·m

5 两种不同柱帽结构形式对弯矩计算值的影响比较

通过对柱帽结构形式的合理调整，调整后的柱上板带和跨中板带在跨中处的弯矩设计值均较调整前有了大幅减小，减小比例约为21%，如表4所示。

表4 柱帽形式对弯矩计算值的影响比较 kN·m

6 采用等代框架法进行验证

6.1 采用等代框架法进行弯矩计算

在前提条件均不变的情况下，采用等代框架法进行上述两种柱帽结构形式的柱上板带和跨中板带跨中弯矩的计算。其中“平托板+斜柱帽”的柱帽结构形式利用刚性角理论(如图2，图3所示)采用1.8 m×1.8 m的方柱进行计算。计算结果如下，其中图4表示采用“平托板柱帽”结构形式，柱上板带和跨中板带的支座及跨中弯矩计算结果；图5表示采用“平托板柱帽+斜柱帽”结构形式，柱上板带和跨中板带的支座及跨中弯矩计算结果。均以内跨“中柱”为研究对象。

6.2 分析比较

从图4和图5的计算统计结果来看，采用“平托板+斜柱帽”的结构形式较“平托板柱帽”，对于中柱而言，柱上板带及跨中板带在支座处弯矩计算值减小18.61%，在跨中处弯矩减小25.08%。支座及跨中平均减小21.85%，同经验系数法在统计结果上接近。具体比较结果如表5所示。

表5 不同结构形式对弯矩设计值的影响 kN·m

7 结语

通过合理改进柱帽的结构形式，增大柱帽在计算弯矩方向的有效宽度c能有效地减小柱上板带及跨中板带在跨中部位的弯矩，达到增加安全储备，合理控制成本的目的。

[1] 李国胜.多高层钢筋混凝土结构设计中疑难问题的处理及算例[M].第2版.北京：中国建筑工业出版社，2011.

[2] GB 50010—2010，混凝土结构设计规范[S].

[3] 北京市建筑设计研究院.建筑结构专业技术措施[M].北京：中国建筑工业出版社，2007.

[4] 理正结构工具箱V5.62版[Z].

The cost influence of column cap structure to floor without beam system

Zhou Wei

(FranshionProperties(China)Limited,Beijing100045,China)

Taking a library project as an example, through the force analysis on column cap in “floor without beam” structure system, pointed out that suitable adjusting column cap structure could make the column cap stress more reasonable, and made the floor without beam structure system had obvious economic advantages.

floor without beam, column cap, rigid angle, punching calculation, bending moment

2014-12-11

周 炜，男，身份证号：132402197801121214，工程师

1009-6825(2015)06-0034-03

TU318

A