面向矢量数据叠加分析的拓扑一致性处理研究

王 少 华,钟 耳 顺,李 绍 俊,3,卢 浩

(1.中国科学院地理科学与资源研究所，北京 100101；2.北京超图软件股份有限公司，北京 100015；3.中国科学院大学，北京 100039)



面向矢量数据叠加分析的拓扑一致性处理研究

王 少 华1,2,钟 耳 顺1,李 绍 俊1,2,3,卢 浩2*

(1.中国科学院地理科学与资源研究所，北京 100101；2.北京超图软件股份有限公司，北京 100015；3.中国科学院大学，北京 100039)

在叠加分析、缓冲区分析、拓扑分析等各种矢量数据分析过程中，首要面对的便是矢量数据拓扑一致性问题。拓扑一致性处理是对GIS矢量数据中由于采集、存储、压缩、转换导致的空间拓扑关系不一致问题进行的拓扑处理,其使得待处理数据在容限范围内具有拓扑一致性，从而便于后续相关分析功能的进行。该文在分析和总结已有拓扑一致性处理算法的基础上，提出了一种更为高效的拓扑一致性处理改进算法，包括弧段间拓扑处理、节点与弧段间拓扑处理、节点间邻近搜索等核心过程。对比实验表明，该算法在保证拓扑一致性处理效果的基础上具有较高的处理性能，是一种实用性较强的拓扑一致性处理算法。

矢量数据；叠加分析；均匀格网索引；拓扑一致性

0 引言

GIS中的叠加分析实质是地理信息图层间的空间关系运算。由于受到数据精度的限制，在地理信息图层叠加分析过程中，不同图层间对象可能出现边界线段不一致问题，极易造成叠加结果产生不符合规范的细碎多边形,如不对其进行有效处理，将引起后续分析计算的异常[1]。因此在进行叠加分析计算时引入了容限概念，从而在矢量数据几何计算中修正与维护数据的拓扑一致性。但单纯通过高精度节点捕捉低精度节点的处理方式很难从根本上避免和消除所有的拓扑不一致情况，因此一种较为系统的解决方案就显得尤为重要。

在拓扑一致性处理和叠加分析过程中存在着大量的计算几何运算，而基于计算几何的算法实现过程主要面临两个挑战：一是计算机在进行数值计算时不可避免的数值精度误差[2]。例如计算几何中经常需要判断点和线段的空间位置关系，在通过求算线段方程判断时，对方程结果是否为零的判断极易出现求算结果略大或略小于零的情况，导致判断失效。程序计算时的精度损失引起的误差一般通过两种方法解决，第一种方法是在中间计算过程中提高表达精度，进行尽可能的“精确”计算[3]，第二种方法是设定对象间的“容限”使得计算结果都在容限范围内[2]。另一种挑战称之为表达误差，由于矢量数据的本质是真实地物对象的映射和模拟，因此在生产矢量数据的过程中不可避免地会引入表达误差，即矢量数据和真实情况的偏移，或称之为矢量数据的不确定性，这种误差同样会导致叠加计算过程出现细碎多边形等异常情况。现有算法中主要通过一种称为“epsilon geometry/tolerance”[4,5]的方法来处理表达误差，即主要通过对待处理数据的规范化来避免误差，且通过“epsilon geometry/tolerance”这一框架，可同时处理数值精度误差和表达误差问题[6,7]。

Milenkovic针对以上问题提出了数据规范化(data normalization)[8]，其解决思路是在计算分析之前对数据进行预处理，用以纠正所存在的拓扑不一致问题。Pullar提出了一种效果较好的解决方案[9]，称之为地图调整(map accommodation)过程,该方法基于Milenkovic算法的思路进行数据调整，但为了避免Milenkovic算法存在的问题，在节点捕捉过程中引入聚类分析的概念。通过对待捕捉的节点进行整体的聚类分析达到改进拓扑一致性捕捉效果的目的，同时也可以通过在聚类分析中增加限制条件，解决多次移动导致的节点偏移过大问题。Harvey等提出了一种控制更加严格的以节点移动为主要方法的拓扑一致性处理算法[10]，该算法主要基于聚类分析实现，通过近似的启发式算法选择节点，要求用户先选择一个数据集中的节点，而后自动调整另一个数据集中的节点与之匹配。ArcGIS的处理模式[11]整体上和Pullar算法接近，且Pullar算法中提及的需要迭代多次操作的情况在ArcGIS中也有体现。

1 拓扑一致性处理改进算法

针对已有的拓扑一致性处理算法存在的不足，本文提出一种性能较优的拓扑一致性处理改进算法，并对算法核心数据结构以及弧段间拓扑处理、节点与弧段间拓扑处理、节点间邻近搜索3个核心处理过程进行详细阐述。

1.1 核心数据结构

(1)均匀格网索引信息结构。在对待处理数据中需进行拓扑一致性处理的各种情况进行搜索查询时，由于均匀格网索引结构实现简单且能有效提升查询性能[12]，因此，本文使用均匀格网索引结构建立空间数据索引，其核心数据结构主要包括以下3个组成部分：

structTopoGridInfo

{

IntnSegmentCount;

TSegmentInfo*pSegmentUnit;

};

structTSegmentInfo

{

IntnDTIndex;

IntnObjIndex;

IntnPntIndex;

IntnPntPos;

};

ArrayPnts

其中：TopoGridInfo为基础的均匀网格索引结构单元结构体，整数类型nSegmentCount记录此网格索引单元中索引的节点(或弧段)数目；TSegmentInfo为基本索引信息结构，其由4个Int型整数构成，其中nDTIndex记录图层索引值，nObjIndex记录该图层中的对象索引值，nPntIndex记录该对象中的节点索引值(当针对弧段建立索引时，即记录弧段的起始节点索引值)，nPntPos记录该节点的索引节点数组Pnts中的位置，数组长度为nPntCount；pSegmentUnit是一个TSegmentInfo类型的指针数组，该指针指向网格索引单元中具体索引的空间数据信息。经过均匀格网索引建立过程后，空间数据中的节点都存储在索引节点数组Pnts中，同时被均匀格网索引单元结构TopoGridInfo管理；而整体的索引结构为单元结构的数组，数组数目即格网索引行数和列数的乘积：

TopoGridInfo*pTopoGridInfo=

newTopoGridInfo[nGridRows*nGridCols]

其中:nGridRows为格网索引行数目，nGridCols为格网索引列数目，行列数目根据待处理数据规模确定。整体索引结构如图1所示。

图1 索引核心结构示意

Fig.1Indexcorestructurediagram

(2)数据调整信息数据结构。为支持多图层间的拓扑一致性处理，本文设计了一种较为简洁统一的数据结构来存储各图层中数据对象需要进行调整的信息，核心数据结构为一个结构体和节点数组：

struct TopoUnitNodeInfo

{

Array nIntersetPntIndex;

Array nIntersetPntPos;

};

ArrayIntersetPnts

每个结构体TopoUnitNodeInfo对应一个待调整的空间对象，nIntersetPntIndex记录该对象需要调整的节点索引(或需要进行节点插入的弧段起始节点索引)，nIntersetPntIndex记录该节点所需调整的坐标在节点数组中的位置，即IntersetPnts中记录的调整结果节点数组的索引。由于拓扑一致性处理方法需支持多图层多对象的处理，因此算法中使用的结构为：

VectorparrTopoUnitNodes

parrTopoUnitNodes长度为所需处理的图层数目，每个图层需要根据其对象数目nObjCount申请所需的内存。

TopoUnitNodeInfo*pTopoUnitNodeInfo=new TopoUnitNodeInfo[nObjCount]

1.2 弧段间拓扑处理

弧段间拓扑处理过程主要是进行弧段与弧段拓扑关系的判别，以及对不满足弧段与弧段间拓扑关系的数据进行修正和维护。当两弧段位置关系出现类似“十字”形的相交情况时，需在两弧段的相交处各插入一个节点，即弧段间的相交情况只允许出现在弧段的起始或终止端点处。此过程基本对应于Pullar算法中的弧段相交情况，但由于Pullar算法中弧段相交过程新增的节点有可能存在和其它弧段造成的二次修正情况，因此把该过程放在第一个流程进行处理，使得新增节点可能导致的和其它弧段或者节点距离小于容限的情况在后续过程中依次进行修正，避免了多次迭代修正的问题。

整体处理过程可以划分为检测和修复两大过程，在检测过程中则对拓扑处理的各图层数据进行遍历查询。通过建立均匀格网索引结构提升弧段间关系判定效率，在建立索引后，依次遍历所有格网索引结构，在一个或周边多个格网范围内进行弧段间相交情况的判定。应注意：当出现两弧段交点距某一弧段起始或终止节点距离在容限范围内的情况时，则此节点不需要插入到两弧段中，而是在后续的节点与弧段拓扑处理过程中进行处理。

如图2所示，弧段L1L2和L3L4相交于点P，但由于点P距离节点L3小于节点容限，因此此时点P不被插入到弧段L1L2和L3L4当中，而将此情况在后面的节点与弧段间拓扑处理过程进行处理。整体处理流程如下：1) 依次遍历矢量数据图层，取出每个对象，根据对象每条弧段位置建立网格索引，索引中记录弧段所属的数据集ID、对象ID、节点索引值等信息，并将所有弧段中节点统一存储到一个节点数组中(相邻两弧段共用的起始终止节点只需存储一次)。2) 索引建立后，遍历所有索引格网，依次取出每个单元格内的弧段，并将此弧段和格网内其它弧段进行相交计算。需注意：如果两弧段交点不在此网格内，则不记录，将此情况交由交点所在网格处理，防止重复记录插入交点。3) 相交计算结束后，按照相交计算记录的交点信息，进行交点插入处理。需注意：当对象某一弧段需添加多个节点时，对新添加的节点排序，根据排序后的顺序添加交点。

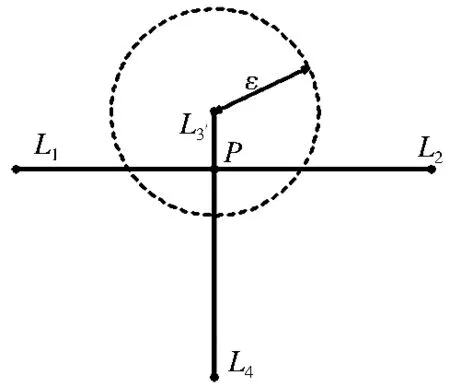
图2 弧段间拓扑处理特殊情况

Fig.2Specialcasesofarcstopologyconsistencyprocess

1.3 节点与弧段间拓扑处理

在节点与弧段间拓扑处理过程中主要是判别节点与弧段的拓扑关系，以及对于不满足节点与弧段拓扑关系的数据进行修正和维护，即当节点距某弧段距离小于容限时，需在弧段上添加此节点的垂足。此过程基本对应于Pullar算法中的弧段插点过程，但由于Pullar算法流程中弧段插点过程理论上存在和其它弧段造成的二次修正情况，因此把该过程放在第二流程进行处理，修正过程由第三过程完成。

整体处理过程同样可以划分为检测和修复两大过程，在检测过程中遍历数据，通过建立均匀格网索引结构提升后续判定速度，在索引建立后，则依次遍历所有格网，在一个或周边多个格网范围内判定节点和邻近弧段的距离。需注意：当出现节点到弧段端点距离小于容限情况时，则无论节点与弧段的距离为多少都不进行插入，而当出现节点到弧段端点距离大于容限，但节点的垂足到弧段端点距离小于容限的情况时，则此垂足点也需插入到弧段中，此情况会在后续的节点间邻近搜索过程中进行处理。

如图3所示，以弧段v1v2为例进行节点与弧段拓扑处理的说明，当节点v距弧段左右两端点v1或v2的距离小于容限，即位于图3中左右端A区域时，无需进行处理，此情况会在后续的节点间邻近搜索中处理。当节点v距弧段端点距离大于容限，但距弧段距离小于容限，即位于图3中C区域时，需要计算节点v到弧段的垂足点，并将此垂足点插入弧段中。有一种特殊情况需要注意：当节点v距弧段端点距离大于容限，但垂足点到弧段端点距离小于容限时，即图3中4个B区域，此时仍需将垂足点插入到弧段中，且后续节点间邻近搜索会处理此特殊情况。整体处理流程如下：1) 依次遍历矢量数据集图层，取出每个对象，将其节点和线段建立网格索引，并将所有节点存储到一个节点数组中。使用两个网格索引结构分别存储所有的节点信息和所有的弧段信息。需注意：节点索引中只需记录节点的坐标信息，无需记录其所属的数据图层、对象、点串索引等信息。弧段存入弧段网格索引结构中，索引结构中需要同步记录该弧段所属的数据图层、对象、点串索引等信息。2) 遍历所有索引网格，依次取出每个索引网格内的节点v，以v为中心点，扩散一个容限的距离，查询是否符合节点插入条件。需注意：如果计算出的垂足点不在当前处理网格内，则不记录，将此情况交由垂足点所在网格处理，防止重复记录所需的插入节点。3) 节点与弧段位置计算结束后，按照记录的节点插入信息，进行数据调整。

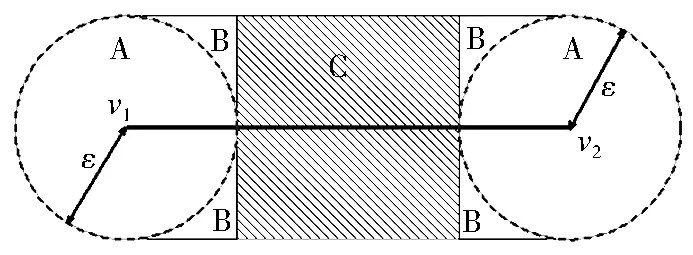
图3 节点与弧段间拓扑处理特殊情况

Fig.3Specialcasesofvertexandarctopologyconsistencyprocess

1.4 节点间邻近搜索

在经过弧段间拓扑处理和节点与弧段间拓扑处理两个过程后，已对数据中的弧段相交情况进行了节点插入，并将数据中存在的节点与弧段距离小于容限的情况通过插入垂足节点的方式转化为距离在容限范围内的节点问题，此时需要通过节点间邻近搜索过程对这些距离在容限范围内的节点情况进行搜索和处理。不同于Pullar算法中的聚类过程，本文采用节点间邻近搜索的策略将这些通过容限相关的节点搜索出来，而后统一调整为同一坐标。

如图4所示，通过节点v1进行邻近点搜索时可将距离v1在容限范围内的节点v2搜索出来，而继续通过v2进行邻近点搜索时可将距离v2在容限范围内的节点v3搜索出来，直到通过v3进行邻近点搜索时不再发现容限范围内的节点为止。找到的v1、v2、v33个节点被称为邻近点簇，如果邻近点簇中节点数目小于用户设置的阈值则直接将这些点调整为与v1点坐标一致，如数目大于用户设置的阈值则将这些点的坐标位置记录下来并反馈给用户进行手动编辑处理。整体处理流程如下：1) 依次遍历矢量数据图层，取出每个对象，对其节点建立网格索引，并将所有节点存储到一个节点数组中。索引结构中需要同步记录该节点所属的数据图层、对象、点数组索引等信息。2) 遍历所有索引网格，依次取出每个索引网格内的节点v，以v为中心点，扩散一个容限的距

图4 节点间邻近搜索

Fig.4Vertexneighboringsearch

离，如找到距离节点v在容限范围内的节点，则以此节点为当前节点继续进行邻近搜索，直到找不到容限范围内的节点为止，而后计算找到的邻近点簇需调整到的节点v1位置。3) 节点间邻近搜索结束后，按照记录的节点调整信息并调整数据。

2 实验与分析

为验证本文算法的有效性，使用C语言实现了上文描述的拓扑一致性处理改进算法，并与ArcGIS桌面软件拓扑一致性处理的相关功能进行测试比较。实验环境为一台主频2.6GHz的双核处理器PC机，内存为2GB。由于叠加分析操作是对矢量数据质量要求较高的分析操作，且在叠加分析操作中涉及大量的节点间匹配计算、弧段间相交计算、多边形生成计算等复杂处理，因此选用叠加分析操作作为拓扑一致性处理效果的验证手段，即在拓扑一致性处理后使用叠加分析操作验证拓扑一致性处理的有效性。首先选取两个面数据，分别在ArcGIS和改进算法中进行拓扑一致性处理和后续叠加分析处理，而后对两种处理结果进行比较分析。为了保证测试验证的有效性，针对该数据分别使用“相交”和“对称差”两种叠加模式，且每种模式下都使用大小不等的两种处理容限进行测试。如表1所示，ArcGIS的拓扑一致性处理和叠加分析操作在同样的叠加模式下对于容限的改变较不敏感，而改进算法中结果对于容限的改变较为敏感。在4组实验中，结果数据集总面积一项中表现出和ArcGIS较好的一致性，ArcGIS处理结果和改进算法处理结果总面积偏差都在十万分之一以下，且有一组测试数据的总面积偏差在百万分之一以下，即经过拓扑一致性改进算法处理后的数据在叠加分析操作过程中表现出较好的数据质量和处理效果。

表1 改进算法和ArcGIS对比测试结果

Table 1 The result comparison of improved algorithm and ArcGIS

序号叠加方式叠加容限ArcGIS总面积(m2)改进算法总面积(m2)面积偏差(m2)1相交5．25461348429912294．371348429614234．562．21042E-072相交0．00011348429912294．371348424580959．503．95374E-063对称差5．25468183976303662．088183956850405．882．37699E-064对称差0．00018183976303662．088183961789600．571．77347E-06

在保证拓扑一致性处理效果的基础上，针对该改进算法的性能与ArcGIS进行进一步的对比测试，为了保证测试的有效性，分别针对常用的线数据类型和面数据类型，选用了多组规模不等的空间数据进行对比测试(表2)。由表2可知，无论是在线数据类型还是在面数据类型对比测试中，在多种数据规模下的改进算法性能都优于ArcGIS中的拓扑一致性处理方法，其中在线数据类型中平均性能提升约为41.75%(图5)，在面数据类型中平均性能提升约为36.94%(图6)。改进算法在保证处理结果有效性的基础上具有较优的处理性能，是一种实用性较强的处理方法。

表2 线和面数据类型性能对比测试结果

Table 2 The comparison of line and polygon dataset performance

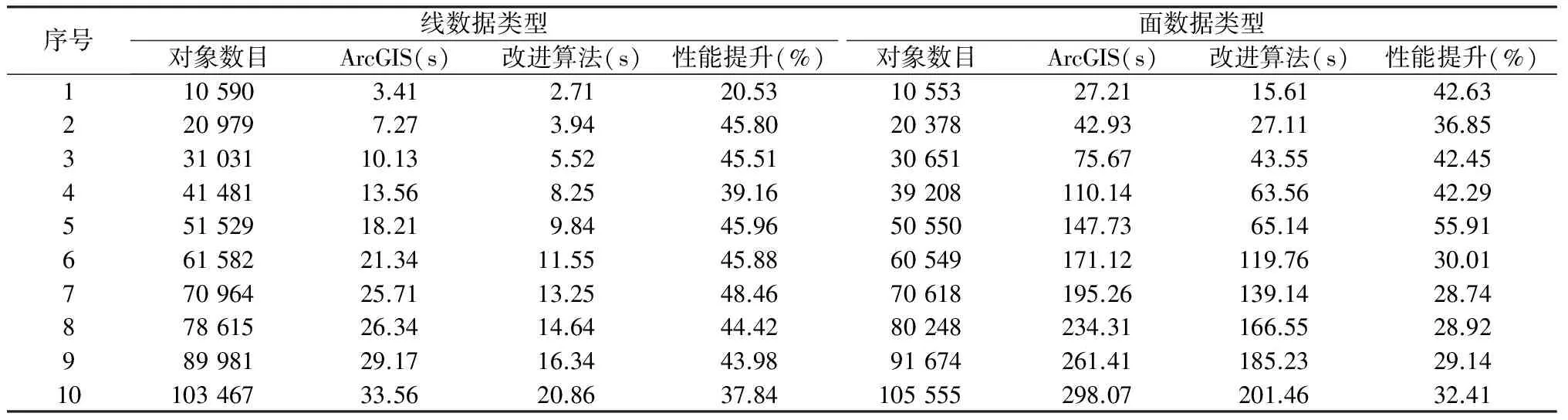
序号线数据类型面数据类型对象数目ArcGIS(s)改进算法(s)性能提升(%)对象数目ArcGIS(s)改进算法(s)性能提升(%)1105903．412．7120．531055327．2115．6142．632209797．273．9445．802037842．9327．1136．8533103110．135．5245．513065175．6743．5542．4544148113．568．2539．1639208110．1463．5642．2955152918．219．8445．9650550147．7365．1455．9166158221．3411．5545．8860549171．12119．7630．0177096425．7113．2548．4670618195．26139．1428．7487861526．3414．6444．4280248234．31166．5528．9298998129．1716．3443．9891674261．41185．2329．141010346733．5620．8637．84105555298．07201．4632．41

图5 线数据集性能对比测试 图6 面数据类型性能对比测试

Fig.5 Comparison of the line dataset performance Fig.6 Comparison of the polygon dataset performance

3 结语

在GIS矢量数据相关的各种空间分析中，拓扑一致性的处理效果与处理性能对于后续包括叠加分析、缓冲区分析、空间查询等各种空间分析效果有较大的影响。本文首先针对已有的较为典型的拓扑一致性处理算法进行了阐述和分析，主要包括Milenkovic算法、Pullar算法、Harvey&Vauglin算法以及ArcGIS的处理方式，重点针对各算法的使用情况以及局限性进行了分析。在此基础上提出了一种性能较优的改进算法，主要包括弧段间拓扑处理、节点与弧段间拓扑处理、节点间邻近搜索3个核心过程，并重点针对处理过程中容限的设置与处理、算法的核心数据结构等内容进行了详细阐述。通过3组实验对该改进算法的处理效果和处理性能进行了对比验证与分析，实验结果表明，本文所描述的改进算法在保证处理效果有效的前提下具有较高的分析处理性能，是一种实用性较强的拓扑一致性处理算法。

[1] GOODCHILD M F.Statistical aspects of the polygon overlay problem[J].Harvard Papers on Geographic Information Systems,1978,6:1-22.

[2] HOFFMANN C M.Geometric and Solid Modeling[M].New York:Morgan Kaufmann,1989.

[3] OTTMANN T,THEIMT G,ULLRICH C.Numerical stability of geometric algorithms[A].Proceedings of the Third Annual Symposium on Computational Geometry[C].ACM,1987.119-125.

[4] BLAKEMORE M.Generalization and error in spatial databases[J].Cartographica,1984,21:131-139.

[5] SALESIN D,STOLFI J,GUIBAS L.Epsilon geometry:Building robust algorithms from imprecise computations[A].Proceedings of the Fifth Annual Symposium on Computational Geometry[C].ACM,1989.208-217.

[6] DOUGENIK J.WHIRLPOOL:A geometric processor for polygon coverage data[A].Proceedings of Auto-Carto 4[C].1980,2:304-311.

[7] CHRISMAN N R.Epsilon filtering:A technique for automated scale changing[A].Technical Papers of the 43rd Annual Meeting of the American Congress on Surveying and Mapping[C].Washington DC,1983.322-331.

[8] MILENKOVIC V J.Verifiable implementations of geometric algorithms using finite precision arithmetic[J].Artificial Intelligence,1988,37(1):377-401.

[9] PULLAR D V.Spatial overlay with inexact numerical data[A].Proceedings Auto-Carto 10[C].Baltimore,1991.313-329.

[10] HARVEY F,VAUGLIN F.No fuzzy creep! A clustering algorithm for controlling arbitrary node movement[A].Proceedings Auto-Carto 13[C].Seattle,ASPRS/ASCM,1997.

[11] ArcGIS 9.3 Help,2009,URL:http://webhelp.esri.com/arcgisdesktop/9.3/index.cfm?TopicName=welcome.2009-12-30.

[12] 王少华,钟耳顺,卢浩,等.基于非均匀多级网格索引的矢量地图叠加分析算法[J].地理与地理信息科学,2013,29(3):17-20.

Study on Topology Consistency Processes for Vector Data Overlay Analysis

WANG Shao-hua1,2,ZHONG Er-shun1,LI Shao-jun1,2,3,LU Hao2

(1.InstituteofGeographicSciencesandNaturalResourcesResearch,CAS,Beijing100101;2.SuperMapSoftwareCo.Ltd.,Beijing100015;3.UniversityofChineseAcademyofSciences,Beijing100039,China)

Topology consistency issues of vector data need to be faced with primary,which in various vector data analysis processes including overlay analysis,buffer analysis and topological analysis.The topology consistency process is handling with inconsistencies of spatial data topological relations,which generated by acquisition,storage,compression and conversion of GIS vector data.It allows data to keep topology consistency within the tolerance range,so as to facilitate subsequent analysis functions.In this paper,a more efficient topology consistency processing improved algorithm is proposed,which is based on analyzing and summarizing the existing topology consistency processing algorithms.The algorithm contains three core processes,including arcs topology processing,vertexes and arcs topology processing and vertexes proximity searching.The comparison experiments show that the algorithm processing performance is improved and can ensure the processing results are correct,and it is a practical topology consistency processing algorithm

vector data;overlay analysis;uniform grid index;topology consistency

2014-01-28；

2014-04-17

交通运输部科技项目(2012-364-X04-102);中国科学院重点部署项目(KZZD-EW-07-01-001);国家科技支撑计划项目(2011BAH06B03);资源与环境信息系统国家重点实验室自主研究项目(088RAC00YA);中国科学院国防科技创新基金项目(CXJJ-14-M13);北京市科技专项(Z141101004414011)

王少华(1983-)，男，博士，主要研究方向为GIS软件技术。*通讯作者E-mail:luhao@supermap.com

10.3969/j.issn.1672-0504.2015.01.003

P208

A

1672-0504(2015)01-0012-05