土地利用结构指标新探及计算程序研究

吴 堑 虹，刘 琼，段 雪 刚

(中南大学有色金属成矿预测教育部重点实验室，地球科学与信息物理学院，湖南 长沙 410083)



土地利用结构指标新探及计算程序研究

吴 堑 虹，刘 琼，段 雪 刚

(中南大学有色金属成矿预测教育部重点实验室，地球科学与信息物理学院，湖南 长沙 410083)

针对目前土地利用结构指标众多，但因对其意义及相互间关系缺少深入分析而出现的普遍复用现象，选取常用表征土地利用数量和空间结构的7个指标，探讨指标间相关性，并对指标意义、分类和模型展开分析和新的探讨。研究表明：原表征土地利用空间格局的多样性指数、优势度指数和均匀度指数应归属于土地利用数量结构指标；因同类指标高度相关，进行土地利用结构分析时在同类指标中择一即可，无需复用；优化的集中化指数模型简化了计算，且能表达区域自身的集中化程度。提出了根据斑块形态差异程度而选择采用算术或加权法进行平均分维数和平均形状指数计算的建议，可使对斑块空间形态特征的测度更为准确；创建的基于斑块拐点数的形态指数模型为描述斑块形态复杂程度提供了新指标。针对目前土地利用结构指标计算软件大而复杂、均为英文界面，且不具备计算数量结构指标的功能，编写了土地利用结构指标的计算程序，可实现各类指标的自动、快速生成。

土地利用结构；指标；相关分析；优化；创建；计算程序

近年来，众多学者对土地利用结构特征进行了定量研究，从不同角度或方法总结出了许多定量表征的指标，但大量有关土地利用的文献或报告普遍存在指标复用现象[1-6]。本文以湖南长江经济带的土地利用数据为基础，开展土地利用结构各类指标的定量分析与相关分析，同时在大量有关文献中随机抽取前人相关的指标数据进行相关性验证，定量化同类指标间的相关程度。在此基础上对指标意义、分类和模型展开深入分析和新的探讨，对指标分类方案进行优化，对部分指标模型进行改进并尝试性地创建新指标模型。针对现有Spatial scaling、Fragstats、APACK、RULE、SIMMAP、Patch Analyst等土地利用结构指标计算软件缺少土地利用数量结构指标的计算功能，且存在大型、复杂、英文界面等不利于基层土地部门对其应用的不利因素，基于VS201 0平台、C#、Microsoft Access 2010进行常用指标计算程序的编写，实现对各类土地利用结构指标的快速计算。

1 数据来源及研究方法

1.1 数据来源

数据源于湖南长江经济带(包括岳阳市的华容县、君山区、岳阳楼区、云溪区、临湘市和岳阳县共6个县市区)2011年土地利用变更数据及2011年1∶50 000 数字化土地利用现状图，以及用于验证指标相关性而抽取到的前人[1-5,7-14]相关的指标数据。

1.2 研究方法

基于前人对土地利用结构指标的常用分类，选取多样化指数和集中化指数进行土地利用数量结构分析；选取多样性指数、优势度指数及均匀度指数进行土地利用空间格局分析；选取分维数、形状指数测度斑块空间特征。对所选取的3类7个指标模型进行公共因子查找，并将查找出的公共因子进行统一表达处理，定性分析指标之间的相关性。

为定量确定指标之间的相关程度，从湖南长江经济带2011年土地利用变更数据中获取各区各地类面积，并将面积数据转换为地类面积百分比，从2011年1∶50 000 数字化土地利用现状图的属性表中获取斑块的面积和周长，按照指标模型计算出湖南长江经济带的3类7个指标，利用SPSS软件对3类指标分别进行相关分析，并结合前人的指标数据进行相关性验证(相关系数均为笔者应用SPSS软件所获得)。

在相关分析基础上，对指标意义和模型展开分析，重新厘定指标分类。运用函数分析法对指标模型的变量及变量之间的关系进行分析，基于GIS功能并结合空间形态基本原理对部分指标模型进行优化或创建。

2 结果与分析

2.1 指标模型分析

3类7个指标模型列于表1，多样化指数和集中化指数模型显示二者的自变量数量及意义虽不同，但其自变量均只涉及地类面积百分比和地类数两个公共因子；多样性指数、优势度指数和均匀度指数同样也只涉及地类面积百分比和地类数两个公共因子，且这3个指标模型的表达式形似，符合数学上线性函数的表达；而分维数与形状指数的自变量均只涉及斑块面积和周长。由此表明同类结构指标之间应存在相关性，下文将通过相关分析对各类指标相关性进行定量测度。

2.2 各类指标相关性分析

2.2.1 数量结构指标相关性 多样化指数和集中化指数相关分析结果(表2)表明二者呈现高度负相关，其中，湖南长江经济带二者的相关系数为-0.979，其它地区的相关系数均在-0.95左右，表明二者在定量测度土地利用数量结构上所起作用相同，互为补充。

表1 指标模型

Table 1 List of index models

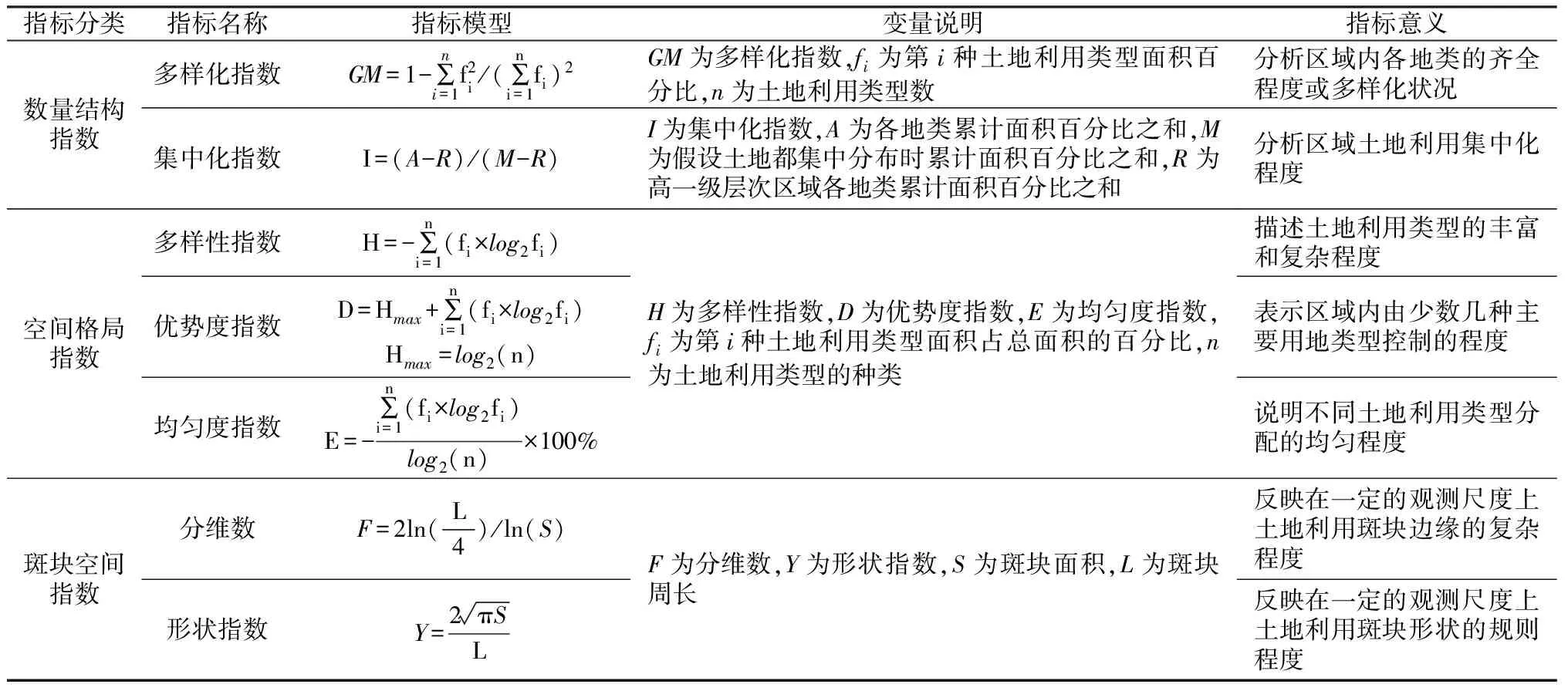
指标分类指标名称指标模型变量说明指标意义数量结构指数空间格局指数斑块空间指数多样化指数GM=1-∑ni=1f2i/(∑ni=1fi)2集中化指数I=(A-R)/(M-R)多样性指数H=-∑ni=1(fi×log2fi)优势度指数D=Hmax+∑ni=1(fi×log2fi)Hmax=log2(n)均匀度指数E=-∑ni=1(fi×log2fi)log2(n)×100%分维数F=2ln(L4)/ln(S)形状指数Y=2πSLGM为多样化指数，fi为第i种土地利用类型面积百分比，n为土地利用类型数I为集中化指数，A为各地类累计面积百分比之和，M为假设土地都集中分布时累计面积百分比之和，R为高一级层次区域各地类累计面积百分比之和H为多样性指数，D为优势度指数，E为均匀度指数，fi为第i种土地利用类型面积占总面积的百分比，n为土地利用类型的种类F为分维数，Y为形状指数，S为斑块面积，L为斑块周长分析区域内各地类的齐全程度或多样化状况分析区域土地利用集中化程度描述土地利用类型的丰富和复杂程度表示区域内由少数几种主要用地类型控制的程度说明不同土地利用类型分配的均匀程度反映在一定的观测尺度上土地利用斑块边缘的复杂程度反映在一定的观测尺度上土地利用斑块形状的规则程度

表2 多样化指数和集中化指数相关系数

Table 2 Correlation coefficient of Gibbs-Martin index and centralization index

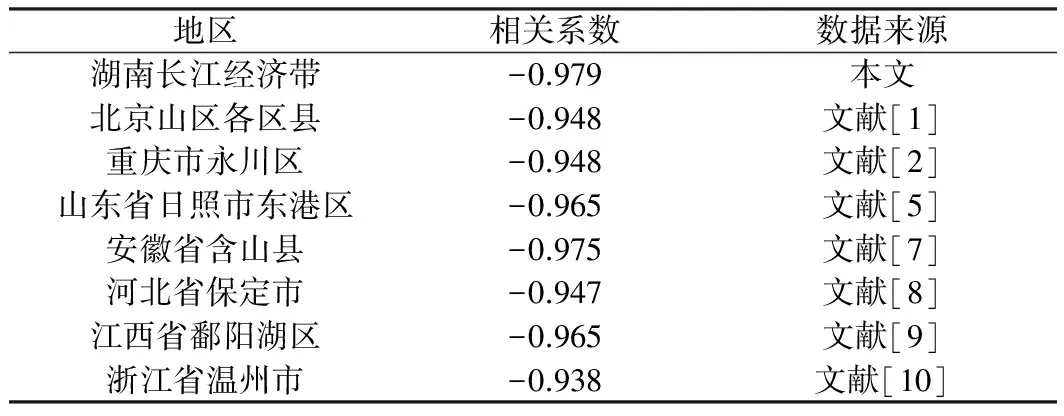
地区相关系数数据来源湖南长江经济带-0．979本文北京山区各区县-0．948文献[1]重庆市永川区-0．948文献[2]山东省日照市东港区-0．965文献[5]安徽省含山县-0．975文献[7]河北省保定市-0．947文献[8]江西省鄱阳湖区-0．965文献[9]浙江省温州市-0．938文献[10]

2.2.2 空间格局指标相关性 土地利用多样性指数、优势度指数和均匀度指数相关分析结果(表3)表明,多样性指数与优势度指数呈高度负相关，二者相关系数介于-0.979～-1；优势度指数与均匀度指数呈高度负相关，相关系数介于-0.984～-1；多样性指数与均匀度指数则呈高度正相关，相关系数均在0.99左右。说明这3个指数从不同的侧面反映同一个问题，互为验证。

表3 多样性指数、优势度指数和均匀度指数相关系数

Table 3 Correlation coefficient of diversity index,dominance index and evenness index

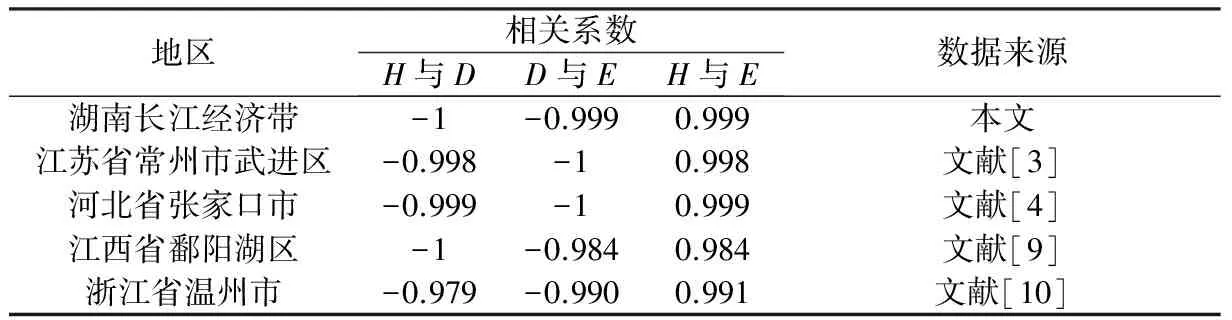
地区相关系数H与DD与EH与E数据来源湖南长江经济带-1-0．9990．999本文江苏省常州市武进区-0．998-10．998文献[3]河北省张家口市-0．999-10．999文献[4]江西省鄱阳湖区-1-0．9840．984文献[9]浙江省温州市-0．979-0．9900．991文献[10]

2.2.3 斑块空间指标相关性 分维数和形状指数相关分析结果见表4，对湖南长江经济带和安徽省含山县各地类平均分维数和形状指数做相关分析，结果显示二者呈高度负相关。此外，对湖南长江经济带和吉林省长岭县各地类的分维数和形状指数分别做相关分析，发现除湖南长江经济带中受人类活动干扰最强的城镇村及工矿用地二者的相关系数为-0.649(中度负相关)外，其它地类二者的相关系数介于-0.931～-0.992，为高度负相关。由此得出分维数和形状指数高度负相关的结论，两者在定量表征斑块形态的复杂程度上所起的作用一致。

表4 分维数和形状指数相关系数

Table 4 Correlation coefficient of fractal dimension and shape index

地区相关系数备注数据来源湖南长江经济带-0．987安徽省含山县-0．805湖南长江经济带-0．649，-0．931～-0．983吉林省长岭县-0．957～-0．992各地类平均分维数和形状指数做相关分析各地类分维数和形状指数分别做相关分析本文文献[7]本文文献[11]

2.2.4 指标相关性分析意义 各类指标相关性分析表明，同类指标高度相关，各类指标在相应测度的土地利用数量或空间结构上所起的作用相同，互为补充和验证。在土地利用结构分析的实际工作中若对每个指标都进行计算，不仅加大了工作量，而且会使得对土地利用结构特征的描述复杂化。笔者建议在进行土地利用结构分析时同类指标择一即可，无需复用。此外，在进行土地利用结构分析时，应根据实际需要和侧重点选取指标。当欲强调区域地类的丰富程度时，可选择多样化指数或多样性指数；当拟强调区域地类集中程度时，可选择集中化指数或优势度指数；而要强调区域不同地类分配的均匀程度时，可选择均匀度指数；分析斑块形态的复杂程度时，则可选择分维数或形状指数。

2.3 空间格局指标重新分类

多样化指数、集中化指数与多样性指数、优势度指数和均匀度指数的公共因子均为地类面积百分比和地类数。此外，虽然这两类指标分属于数量、空间结构指标，但其表达的意义相似，应有密切相关性。在两类指标中分别选取一个指标进行跨类相关分析，以确定其相关程度，结果见表5。

表5 多样化指数和多样性指数相关系数

Table 5 Correlation coefficient of Gibbs-Martin index and diversity index

地区相关系数数据来源湖南长江经济带0．991本文江西省鄱阳湖区0．976文献[9]浙江省温州市0．989文献[10]

相关性计算表明多样化和多样性指数呈高度正相关。其它指数的两两相关分析(因篇幅原因，不一一列表)的相关系数绝对值也均在0.9以上，故得出两类指标间存在高度相关性。基于两类指标间存在高度相关性、指标模型的公共因子均为地类面积百分比和地类数以及指标意义相近，笔者认为原表征土地空间格局的多样性指数、优势度指数和均匀度指数用于表达土地利用数量结构更为合适。

2.4 部分指标优化

2.4.1 集中化指数的优化 对集中化指数模型进行分析，发现该指标是通过建立区域与上级区域的土地利用集中化程度的关系来表征区域的集中化程度，而其他表征数量结构的指标均未涉及上级区域，均为区域本身的数量结构，因此表征土地利用数量结构的指标间不具有可比性。此外，集中化指数不能独立表达区域本身的集中化程度，且其模型表达式尽管简单，但其包含3个变量，这些变量还暗含2个次级变量，故其计算繁琐。对原有模型进行优化，其表达式为：

I优=A/n

式中：A仍为各地类(按照地类面积百分比由高到低顺序排列，即对地类面积百分比进行Huffman编码)累计面积百分比之和，n为土地利用类型数。

优化后的模型变量数由原来的5个减至2个，大大简化了计算，而且能独立、准确地表达区域自身的集中化程度。

2.4.2 平均分维数和平均形状指数的优化 前人在计算某一地类或区域的平均分维数和平均形状指数时，多采用该地类或区域所有斑块的分维数和形状指数的算术平均值，这种处理方法在某一地类或区域内各斑块形态接近时具有简便的优点。但在实际情况中，某一地类或区域内的斑块形态一般存在不定差异，其差异主要体现为斑块面积及周长大小的不同，笔者认为为了更准确地表达某一地类或区域的平均分维数和平均形状指数，可将斑块面积及周长作为权重因子加入到计算中。其表达式为：

F均=∑(Fw) ,Y均=∑(Yw)

式中：F均、Y均分别为某一地类或区域的平均分维数、平均形状指数；F、Y分别为斑块分维数、斑块形状指数；w为斑块综合权重，其模型可表达为：

w=w1(Li/∑Li)+w2(Si/∑Si)

式中：w1为斑块长度权重系数，w2为斑块面积权重系数，Li为第i种地类或区域单个斑块长度，Si为第i种地类或区域单个斑块面积。

显然当某一地类或区域内的斑块形态存在较大差异时，加权平均法计算结果更贴近真实情况，但该方法的缺点是计算量明显增加，且权重系数的确定有层次分析法、综合评价法和专家评价法等多种方法，也使工作量大大增加，但增加的工作量可以通过编程方法实现自动计算来解决(有待进一步研究)。所以笔者建议在开展研究斑块空间形态特征的工作时，应先对同一地类或区域内的所有斑块面积或周长做频率分布直方图，若频率分布直方图服从或近似服从正态分布，则可采用算术平均法；反之，则应采用加权平均法。

2.5 新指标创建尝试

分维数、形状指数是最常见的测度斑块形态特征的指标，其模型中均只包含斑块面积和周长两个因子。实际上斑块的拐点数同样可以反映斑块形态的复杂程度，且单位周长或面积上的拐点数越多斑块形态越趋复杂。现有的GIS软件具有自动提取斑状拐点数的功能，因此笔者认为可以斑状拐点数作为变量，构建斑块形态指数模型，其表达式为：

T=N/ln(L) 或T=N/ln(S)

式中：T为斑块形态指数，N为斑块的拐点数，L为斑块的长度,S为斑块的面积。

在计算某一地类或区域的平均形态指数时，先进行相关优化，若要采用加权平均法，则需构建权重模型。斑块权重w模型为：

w=Li/∑Li或w=Si/∑Si

式中：Li为第i种地类或区域单个斑块长度，Si为第i种地类或区域单个斑块面积。

原有的分维数、形状指数是基于周长-面积法，创建的形态指数是基于拐点数-周长法或拐点数-面积法，而数学上曲线的凹凸用拐点表达，故笔者认为该法在定量测度斑块形态特征上更为准确。

3 土地利用结构指标计算程序开发

基于VS2010平台、C#、Microsoft Access 2010进行土地利用结构指标计算程序开发。基于各参数的关联性，绘制E-R图(图1)，数据库包括行政区各地类面积表(从土地利用变更数据中获取)和各地类斑块表(从土地利用现状图的属性表中获取，提取面积和周长)。根据数据流程(图2)分析，采用C#提供“OleDb”接口实现对Access数据库连接及功能集成。基于人-机友好原则将复杂的指标计算功能设置于后台运行，实现使用者在界面对拟计算的指标进行勾选就可自动完成计算，且结果数据以表格形式自动展示，并可以Excel格式导出(图3)。

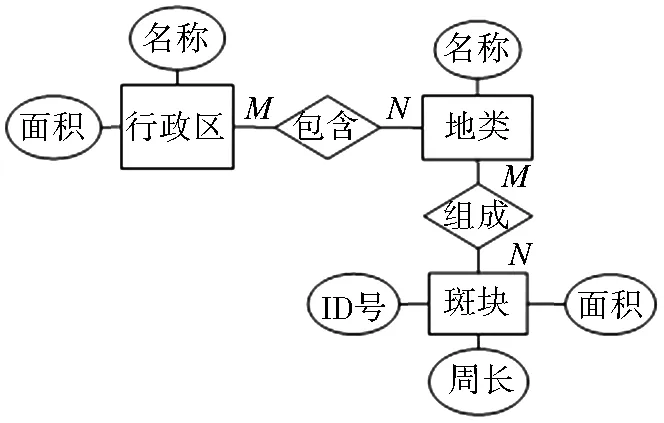
图1 E-R图

Fig.1 E-R diagram

4 结论

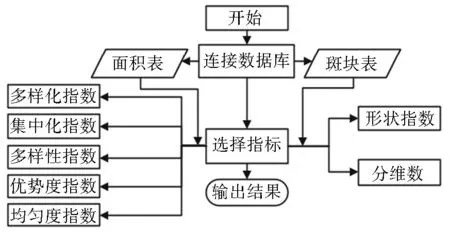
图2 土地利用结构指标计算程序流程

Fig.2 Calculation program flowchart of land use structure indices

图3 土地利用结构指标计算程序界面

Fig.3 Calculation program interface of land use structure indices

以湖南长江经济带为例，同时结合前人的指标数据，开展对土地利用结构常用指标的重新认识、优化及指标自动计算等工作，结论如下： 1)原表征土地空间格局的多样性指数、优势度指数和均匀度指数应归属于土地利用数量结构指标，因同类指标高度相关，进行土地利用结构分析时同类指标择一即可，无需复用；2)集中化指数模型的优化不仅具有表达及计算简单的优势，而且能独立且准确表达区域自身的集中化程度；3)提出的根据斑块周长或面积频率分布直方图特征选择采用算术平均法或加权平均法进行平均分维数和平均形状指数计算的建议，使得对斑块空间形态特征的测度更为准确；4)创建的基于斑块单位长度或面积上的拐点数的斑块形态指数模型，为描述斑块形态复杂程度提供了新的参考指标；5)计算程序为中文界面、平台简单、操作可行，实现了土地利用结构指标的自动、快速生成，具有应用价值。

中南大学数学与统计学院侯木舟教授对本文提出了专业指导，此致谢忱！

[1] 王秀丽,关小克,薛剑.北京山区区县土地利用结构定量分析及农业产业研究[J].中国农业资源与区划,2013,34(2):85-91.

[2] 施开放.西南丘陵山区县域土地利用结构特征研究——以重庆市永川区为例[D].重庆:西南大学,2013.

[3] 张群,张雯,李飞雪,等.基于信息熵和数据包络分析的区域土地利用结构评价——以常州市武进区为例[J].长江流域资源与环境,2013,22(9):1149-1155.

[4] 郭洪峰,许月卿,田媛.张家口市土地利用结构特征及其动态变化[J].水土保持通报,2013,33(3):259-264.

[5] 魏鲁,张兰梅,郭晨.日照市东港区土地利用结构与空间布局分析[J].山东国土资源,2011,27(3):54-56.

[6] 林源,刘木生,林联盛,等.赣州市土地利用结构定量分析[J].江西科学,2009,27(3):360-364.

[7] 陈其春,吕成文,李壁成,等.县级尺度土地利用结构特征定量分析[J].农业工程学报,2009,25(1):223-231.

[8] 赵志革,赵明,杨庆朋.保定市土地利用结构定量分析[J].江西农业学报,2007,19(11):89-92.

[9] 刘桃菊,蔡海生,邵建英,等.鄱阳湖区的土地利用结构定量分析[J].江西农业大学学报,2003,25(6): 934-938.

[10] 朱凤武,彭补拙,丁建中,等.温州市土地利用空间格局研究[J].经济地理,2001,21(1):102-104.

[11] 王平,卢珊,杨桃,等.地理图形信息分析方法及其在土地利用研究中的应用[J].东北师范大学学报(自然科学版),2002,34(1):93-99.

[12] 王爱民,刘加林,缪磊磊,等.人地关系研究中的土地利用特征指标分析[J].经济地理,1999,19(1):62-66.

[13] 傅伯杰.黄土区农业景观空间格局分析[J].生态学报,1995,15(2):113-120.

[14] 曹天邦,朱晓华,肖彬,等.土地利用类型分布的分形结构及其应用——以江苏省扬中县丰裕镇为例[J].地域研究与开发,1999,18(4):9-12.

New Exploration and Calculation Program Research of Land Use Structure Indices

WU Qian-hong,LIU Qiong,DUAN Xue-gang

(KeyLaboratoryofMetallogenicPredictionofNonferrousMetals,MinistryofEducation,SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China)

In view of the current there are many indices for land use structure,the lack of deep analysis of their significance and mutual relations results in widespread mix-use.The authors selected 7 indices which were commonly used to express the quantitative and spatial structure of land use to investigate the correlation between the indices.In addition,expanding analysis and new exploration in significance,classification and model of the indices were done.Result shows: diversity index,dominance index and evenness index which were used to express the spatial pattern of land use should be attributed to the quantitative structure indicators of land use.Owing to the high correlation between similar indices,one index of similar indices should be selected to analyze structure of land use without mix-use.The optimized centralization index model can simplify the calculation,and can express the extent of its own regional centralization.According to the differences degree in plaque morphology,the arithmetic method or the weighted average method should be chosen to calculate the average fractal dimension and the average shape index.This proposal makes plaque morphology measure more accurate.The created morphology index model which is based on the number of inflection of plaque provides a new index to describe the complexity of plaque morphology.The present calculation softwares of land use structure indices are large,complex,English interface,and can′t calculate the indices of quantitative structure.The paper programs calculation procedure of land use structure indices,various types of indices of land use structure can be automatically and quickly calculated.

land use structure;indices;correlation analysis;optimization;creation;calculation procedures

2014-04-30；

2014-08-05

湘江水环境重金属污染整治关键技术研究与综合示范项目(2009ZX07212-001-06)

吴堑虹(1957-)，女，博士，教授，主要从事GIS教学及其在地学中的应用研究。 E-mail：qhwu19@163.com

10.3969/j.issn.1672-0504.2015.01.023

F301.23;TP319

A

1672-0504(2015)01-0110-05