一种基于模糊相似度的球面格网几何变形评价指标

张 斌，苑 争 一，赵 学 胜，张 新 建

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)



一种基于模糊相似度的球面格网几何变形评价指标

张 斌，苑 争 一，赵 学 胜，张 新 建

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

全球离散格网模型的不确定性，包括格网单元的几何变形及空间分布问题，是制约其广泛应用的主要因素之一。该文从三角形相似的角度出发，构造了球面三角格网的模糊相似度评价指标，以此对球面四元三角格网模型的几何变形特征及其收敛性进行分析评价，并给出了格网单元变形在八面体单元和全球区域的位置分布规律。最后，与传统评价指标进行对比实验，结果表明：该指标不但能够反映剖分模型的几何变形分布，而且还具有两大优势：1)能够同时反映剖分单元的几何形状和面积变形，可作为格网形状和面积变形的综合评价指标；2)该指标是相对于不同递归层次上理想剖分单元的绝对变形量，相比其他统计量，更便于表达不同层次间的格网几何变形。

全球离散格网；球面四元三角网；格网几何变形；模糊相似度

0 引言

近年来，全球离散格网(Discrete Global Grid,DGG)模型的提出，为构建大范围、多分辨率、全球统一无缝的空间定位基础框架提供了新思路[1,2]。尽管国内外学者在全球离散格网的剖分类型、索引结构及建模方法等方面取得了丰富成果，但是由于格网单元的不均匀性及其变形分布的不规则性，很难进行变形误差的传播和控制，使其在不同领域的应用受到极大的限制。

目前，针对球面格网单元几何变形评价和分析的研究成果，大致可分为三类：第一类是对格网评价标准的研究。这些标准最早由Goodchild于1992年提出，被称为“Goodchild标准”[3]，后经不断补充和修改，Kimerling等[4]把它确定为研究全球格网划分所遵循的一般标准。该标准共有14条，可以作为对全球离散格网系统的理想描述。第二类是对格网评价指标的研究，基于“Goodchild标准”构造可以量化的格网评价指标，进而通过分析各指标值来寻找格网模型的几何变形特征。例如，Heikes等[5,6]在应用全球离散格网进行大气建模的过程中，构造了“Cell Wall Midpoint Ratio”指标；Gregory等[7]基于“参考点到邻近格网是等距的”及“任何两个邻近格网的边是连接两个格网中心的大圆弧平分线”这两条标准，构造了“Coefficient of Variation(CV)”和“Cell Wall Midpoint Ratio”两个指标，并应用这些指标对比分析了几种剖分模型的变形特征。第三类是基于格网结点分布的研究，从格网结点的分布特性出发，对比分析不同剖分模型的均匀性特征。例如，明涛等[8]通过计算每个格网结点到邻近结点的距离、结点与两邻近结点间连线的夹角，作为格网结点空间分布均匀性的评价标准；周良辰等[9]通过计算球面格网总的电势能来评价格网结点分布的均匀性。

本质上看，部分理想格网的标准是相互矛盾的，任何一个全球离散格网系统在数学上不可能同时满足上述全部指标，一个比较优秀的格网系统应该根据具体的应用条件选择一个合理的平衡。然而目前的研究仅限于探讨不同球面格网几何特征(长度、面积、角度等)的总体变化及收敛性特征[10-17]，缺乏对不同位置上的变形分布规律的研究[18,19]；另外，对于不同剖分层次上的理想剖分单元，一些传统的格网变形评价指标(如密实度)的取值是变化的，不适合层次间格网几何变形的比较分析。为此，本文在相似三角形原理的基础上，把平面三角形模糊相似度扩展到球面上，构造了一个“球面格网模糊相似度”评价指标，并通过计算实际剖分单元相对于理想剖分单元的模糊相似度，来评定格网的形状和面积综合变形特征，进而分析其在球面上的位置分布规律，为构建全球离散格网变形的评价体系及数据质量控制提供参考。

1 球面三角形的模糊相似度

1.1 模糊相似度基本原理及其改进方法

根据三角形相似原理构造平面三角形相似模糊度[20]，用于判定两个三角形是否相似，基本原理为：如果一个三角形的一个内角为a，则在另一个三角形的对应角x和该角的差异性应遵循以下正态分布：

d(x)=e-k(x-a)2

(1)

大于0的系数k可由下式计算：

(2)

式中:a*Pa为正态分布的3σ点，这里令Pa为50%。这样对角度的相似度可由下式得到：

Ia=cosn(ks(1-d(x)))

(3)

基于余弦曲线的特征，可定义n=3，ks=π/2。对于一对三角形，可先利用式(3)分别计算3个内角的相似度，而后利用式(4)计算整个三角形的相似度。

It=k1Ia+k2Ib+k3Ic

(4)

通常取k1=k2=k3=1/3，即取3个内角相似度的算术平均值作为整个三角形的模糊相似度，但这容易受极大值的影响，使得所求三角形的模糊相似度偏大。而几何平均值受极大值的影响小于算术平均值，且几何平均值更适用于求比率(大于0小于1)的均值,因此，采用几何平均值代替上述算术平均值，作为整个三角形的模糊相似度，计算公式如下：

(5)

1.2 模糊相似度在球面三角形的扩展

把上述平面三角形的模糊相似度扩展到球面上。 从球面几何可知，没有一种剖分方法能使球面格网在每个层次上获得像平面栅格那样完全相同的几何特征(如：面积、长度、角度)，只能达到近似相等[13]。对于球面三角剖分，理想的剖分单元应当满足面积相等、几何形状相同(即球面正三角形)。由球面三角形面积计算式(8)可知，球面三角形的内角和不是定值，因此需要计算每一层的理想剖分单元的内角，进而计算每一个剖分单元的内角，并带入模糊相似度计算公式求解每个球面三角形单元的模糊相似度。具体过程如下：

(1)用球面面积除以每一层剖分的格网单元的个数，得到该层理想剖分单元的面积，进而根据球面三角形面积和式(8)反算出理想剖分单元的内角，经计算可得理想剖分单元的面积和内角的计算如式(6)、式(7)所示，其中n为剖分层次，R为球半径。

Sideal=4×PI×R2/(8×4n)

(6)

(7)

S=R2×(A+B+C-π)

(8)

(2)设A、B、C为球面上任意3点，X1、X2、X3分别为A、B、C 3点的向量(笛卡尔坐标系)，则球面三角形ABC的内角ai为：

(9)

(3)将球面三角形单元的内角ai及理想剖分单元的内角Aideal带入式(1)—式(3)，分别求得三角形单元3个内角的模糊相似度Ia、Ib、Ic，由式(5)求出该球面三角形的模糊相似度。式(8)为球面三角形的面积公式，其中E=A+B+C-π为球面三角形角超，A、B、C为球面三角形的3个内角。角超反映了球面几何与平面欧式几何的差异，在平面几何中三角形内角和等于π，角超等于0，三角形面积与角超没有关系；在球面几何中，三角形的内角和大于π，角超大于0，三角形的面积随角超的变化而变化。

在球面几何中，有“对应角相等的两个球面三角形全等”的判定定理，即模糊相似度为1的两个球面三角形，其对应角和面积均相等，两个三角形全等。因此将平面三角形的模糊相似度扩展到球面上后，该指标既能反映出剖分单元几何形状的变形，又能反映出面积的变形。面积形状均无变形的剖分单元，模糊相似为1，其他情况下都小于1。

2 实验设计及结果分析

2.1 实验设计

本实验以基于正八面体的QTM剖分为例，采用面积近似的“经纬度平分法”剖分，直接采用经纬度平均值作为新的结点。以正八面体的一个原始球面三角形ABC为例，A与极点重合，其他两个顶点位于赤道上，具体剖分过程如下：1)将正八面体每个原始球面三角形的两个大圆弧(AB和AC)剖分成2n个相等的部分，分别得到2n-1个新点{p1,p2,…,p2n-1}和{q1,q2,…,q2n-1};2)沿纬线分别连接pi和qi，然后对纬线进行i等分，得到2i-1个新点，其中i∈[1,2n](当i=2n+1时，弧piqi对应于BC)；3)用大圆弧线连接邻近3个球面点，得到第n层的球面剖分。剖分效果如图1所示[11]。选取球面格网模糊相似度(similarity)及其传统的密实度(compactness)和格网单元面积，作为剖分单元形状和面积的变形指标，对比分析各指标随剖分层次的变化及其分布特征。

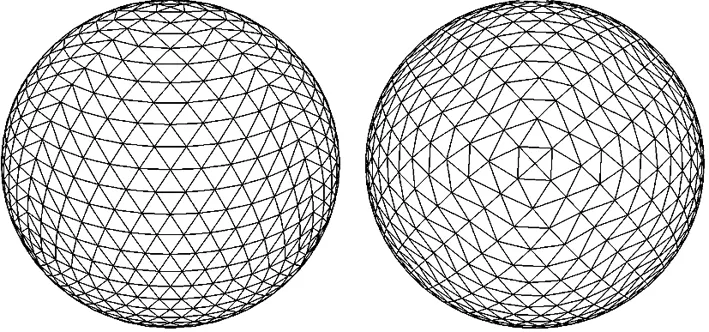
图1 O-QTM剖分模型(第5层)

Fig.1O-QTMsubdivisionmodel(infifthlevel)

传统密实度是通过表面积和周长的比值来测定。为了便于比较不同剖分模型、不同剖分层次该指标的变化，Kimerling等[12]对上述指标进行了标准化处理，即选取与格网等面积、以极点为中心的球形区域的密实度作为比较对象，用格网单元的密实度去除球形区域的密实度，得到区域标准化密实度(ZSC)，计算公式如下：

(10)

式中:cell area为格网单元的面积，cell perimeter为格网单元的周长，zoon area为与格网等面积、以极点为中心的球面区域的面积，zoon perimeter为球形区域的周长，r为球半径。

2.2 结果分析

剖分单元面积、单元密实度、模糊相似度的最大、最小值比(Max/Min)及标准差(SD)随剖分层次的变化见表1所示。

表1 各指标在不同剖分层次的取值

Table 1 Index values in different levels

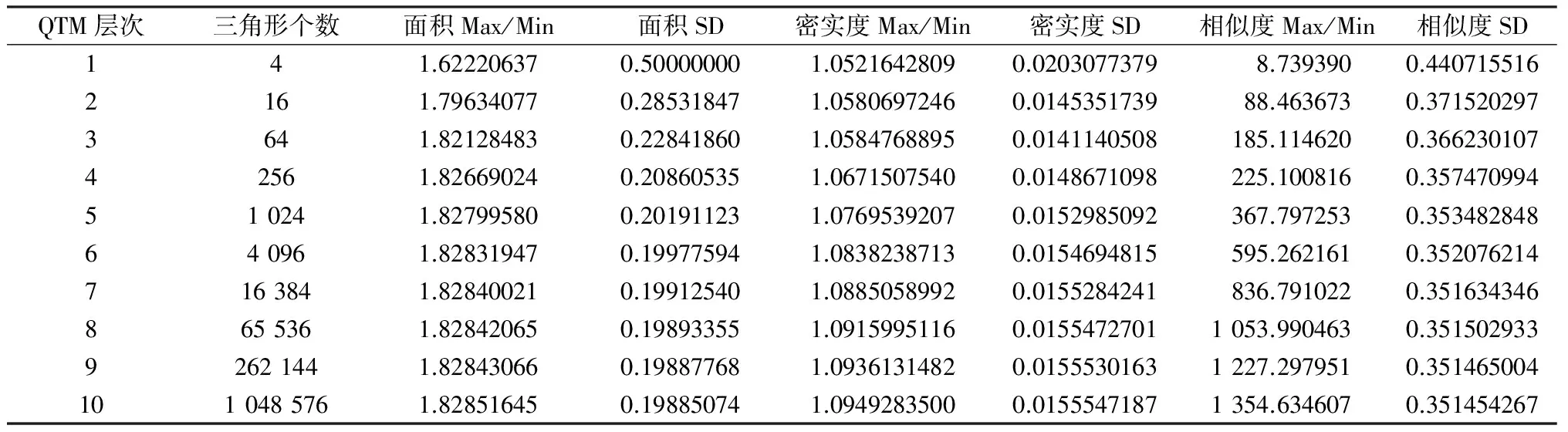
QTM层次三角形个数面积Max/Min面积SD密实度Max/Min密实度SD相似度Max/Min相似度SD141．622206370．500000001．05216428090．0203077379 8．7393900．4407155162161．796340770．285318471．05806972460．014535173988．4636730．3715202973641．821284830．228418601．05847688950．0141140508185．1146200．36623010742561．826690240．208605351．06715075400．0148671098225．1008160．357470994510241．827995800．201911231．07695392070．0152985092367．7972530．353482848640961．828319470．199775941．08382387130．0154694815595．2621610．3520762147163841．828400210．199125401．08850589920．0155284241836．7910220．3516343468655361．828420650．198933551．09159951160．01554727011053．9904630．35150293392621441．828430660．198877681．09361314820．01555301631227．2979510．3514650041010485761．828516450．198850741．09492835000．01555471871354．6346070．351454267

2.2.1 剖分模型收敛性分析 根据表1数据绘制随剖分层次增加的格网变形趋势图(图2-图4)。从图2和图3可以看出，随着剖分层次的增加，格网面积及密实度的最大、最小值之比逐渐增大并趋于稳定；指标的标准差逐渐减小并趋于稳定。从图4可以看出，尽管模糊相似度的最大、最小值比的收敛性较差，但该指标的标准差收敛性较好。这表明该指标对极值较为敏感，但随着剖分层次的增加，格网间的差别逐渐减小，模型的稳定性良好，格网变形是收敛的。

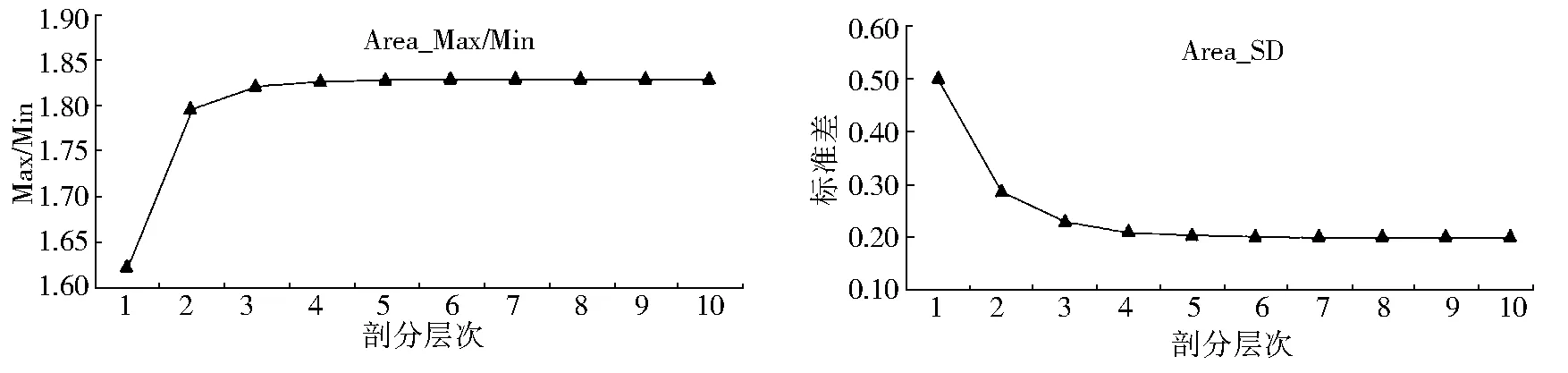
图2 格网面积最大最小值比、标准差随剖分层次的变化

Fig.2 Variations of Area_Max/Min and Area_SD in different levels

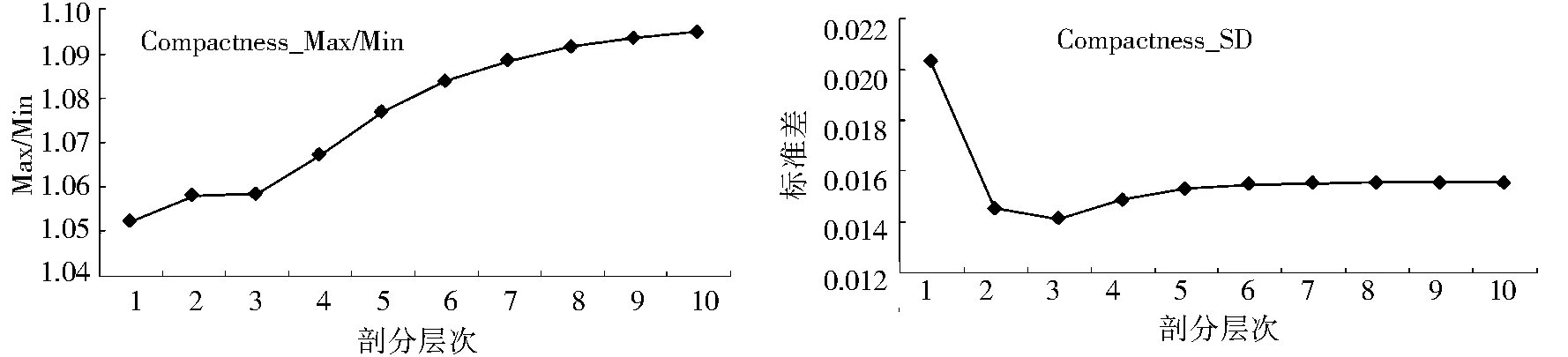
图3 格网密实度最大最小值比、标准差随剖分层次的变化

Fig.3 Variations of Compactness_Max/Min and Compactness_SD in different levels

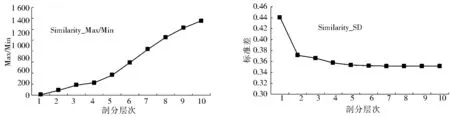
图4 格网相似度最大最小值比、标准差随剖分层次的变化

Fig.4 Variations of Similarity_Max/Min and Similarity_SD in different levels

2.2.2 格网变形在八面体上的位置分布 以八面体的一个单元面为例，将球面剖分5层，计算各剖分单元的以上3种指标值，并借助可视化方法直观地展现在球面上，进而分析球面上不同位置的变形分布规律。图5a显示了剖分单元面积变形率(相对于理想剖分单元)在球面上的分布规律，深色区域的变形率较小，主要分布在八面体的中间区域，呈带状分布；往极点和赤道方向逐渐变大。图5b显示了格网单元密实度在球面上的分布规律，其中深色区域的密实度较小。从图中可以看出八面体中心区域的密实度较大，即格网形状较规则，接近于理想剖分；从中心向八面体的3个顶点逐渐减小，变形逐渐增大。图5c显示了格网单元模糊相似度在球面上的变化规律，其中深色区域的模糊相似度较小。图中八面体中心区域模糊相似度最大，即最接近理想剖分；从中心向八面体3个顶点方向逐渐减小，变形增大。

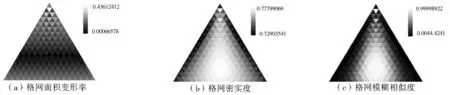
图5 三种变形指标在八面体上的位置分布

Fig.5 Location distributions of three deformation indices on the octahedral

2.2.3 特定格网单元评价指标的取值及其变化分析 为了体现模糊相似度在评价格网变形方面的综合性特征，抽取特定的格网单元，定量分析三种指标(面积、密实度、模糊相似度)的差别。如图6所示，以八面体的一个面为例，剖分4层，得到256个球面三角形，取中央经线上三角形单元，分别计算上述各格网单元的三种指标值。为了便于对比分析，将各指标分别进行归一化处理，计算结果见表2。根据表2中的数据绘制指标变化曲线(图7)。由图7可知：1)从赤道到两极，沿中央经线，随着纬度的增加，密实度和模糊相似度指标都逐渐减小，极点附近区域震荡现象明显；2)格网的面积变形先随纬度增加减小，后又增加，极点附近区域震荡现象明显；3)模糊相似度指标同密实度指标的变化趋势一致，其变化曲线介于密实度和面积变形指标之间。

3 结语

本文从三角形相似的角度出发，构造了球面三角形模糊相似度评价指标，用于评价不同剖分层次上的实际剖分单元与理想剖分单元间的差异，并与传统的密实度和面积变形指标在O-QTM剖分的变形收敛特性及空间分布特性进行了对比。实验及分析表明：1)球面模糊相似度指标同其他指标一样，能够反映剖分模型的收敛规律，其分布特征同密实度指标相似，能够很好地反映格网几何形状变形的分布规律；2)由于球面三角形的面积受其内角和的影响，该指标还能够间接地反映出格网的面积变形，可作为衡量格网形状和面积变形的综合评价指标；3)该指标是相对于理想剖分单元的绝对变形量，相比于其他统计量，更便于表达不同剖分层次间格网的几何变形。因此，无论是在评价指标的综合性，还是层次间的可比较性方面，球面模糊相似度指标都要优于传统的密实度等变形评价指标。

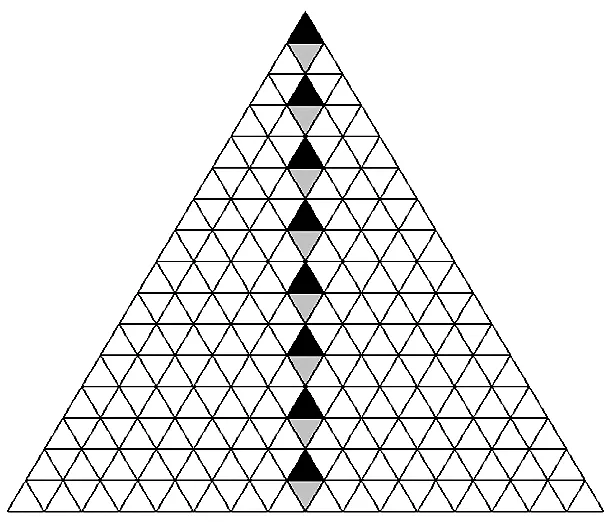
图6 特定测试单元

Fig.6 Specific test grids

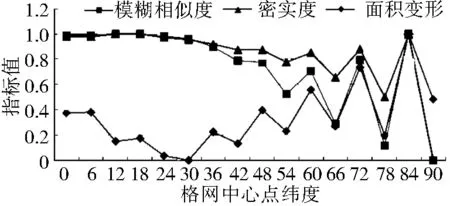
图7 特定格网上的各个指标变化曲线

Fig.7 The changing curve of each index on specific grids

表2 中央经线(45°)上的格网指标值

Table 2 Index values of grids on the central meridian

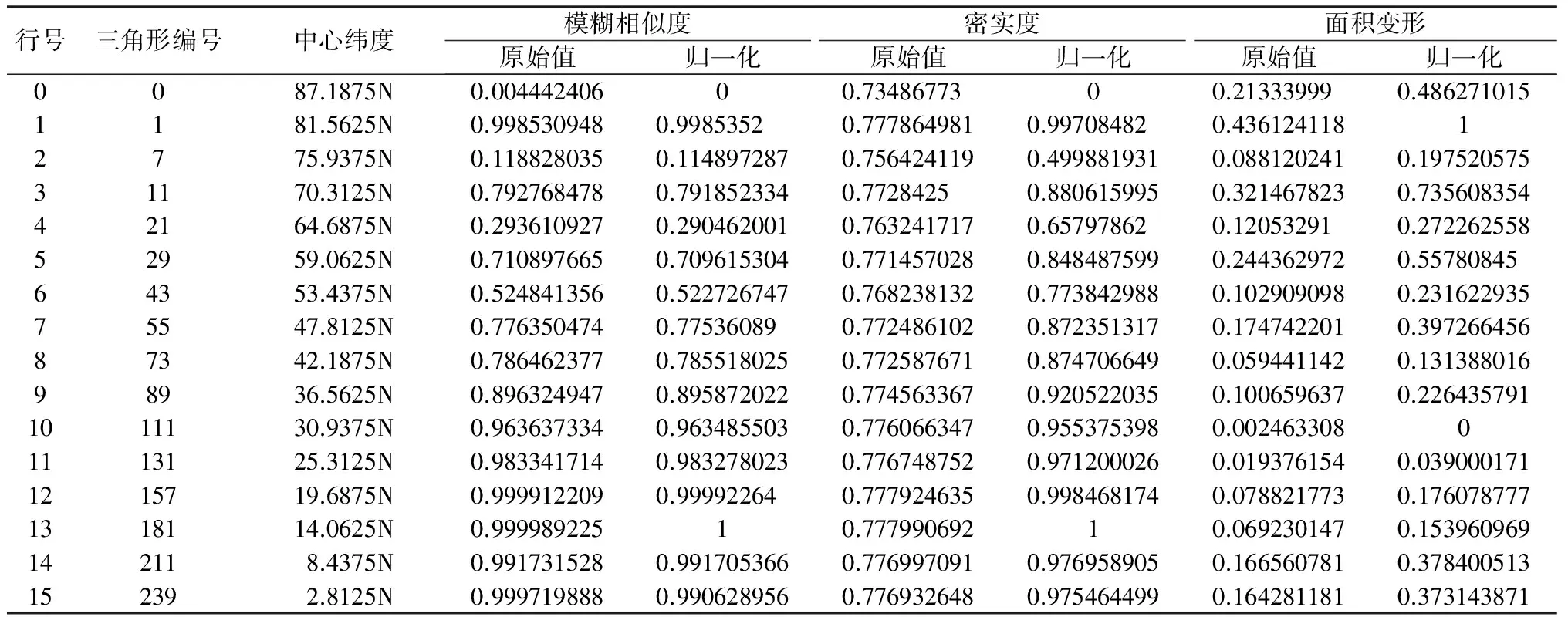
行号三角形编号中心纬度模糊相似度密实度面积变形原始值归一化原始值归一化原始值归一化0087．1875N0．00444240600．73486773 00．21333999 0．4862710151181．5625N0．9985309480．9985352 0．7778649810．99708482 0．43612411812775．9375N0．1188280350．1148972870．7564241190．4998819310．0881202410．19752057531170．3125N0．7927684780．7918523340．77284250．8806159950．3214678230．73560835442164．6875N0．2936109270．2904620010．7632417170．657978620．12053291 0．27226255852959．0625N0．7108976650．7096153040．7714570280．8484875990．2443629720．5578084564353．4375N0．5248413560．5227267470．7682381320．7738429880．1029090980．23162293575547．8125N0．7763504740．775360890．7724861020．8723513170．1747422010．39726645687342．1875N0．7864623770．7855180250．7725876710．8747066490．0594411420．13138801698936．5625N0．8963249470．8958720220．7745633670．9205220350．1006596370．2264357911011130．9375N0．9636373340．9634855030．7760663470．9553753980．00246330801113125．3125N0．9833417140．9832780230．7767487520．9712000260．0193761540．0390001711215719．6875N0．9999122090．999922640．7779246350．9984681740．0788217730．1760787771318114．0625N0．99998922510．77799069210．0692301470．153960969142118．4375N0．9917315280．9917053660．7769970910．9769589050．1665607810．378400513152392．8125N0．9997198880．9906289560．7769326480．9754644990．1642811810．373143871

[1] DUTTON G.A hierarchical coordinate system for geoprocessing and cartography[A].Lecture Notes in Earth Sciences[C].Berlin Springer-Verlag,1999.

[2] LUKATELA H.Ellipsoidal area computations of large terrestrial objects[A].The First International Conference on Discrete Grids′2000[C].2000.

[3] GOODCHILD M F.Criteria for evaluation of global grid models for environmental monitoring and analysis[R].NCGIA Technical Report,1994.9-47.

[4] KIMERLING J A,SAHR K,WHITE D,et al.Comparing geometrical properties of global grids[J].Cartography and Geographic Information Science,1999,26(4):271-288.

[5] HEIKES R,RANDALL D A.Numerical integration of the shallow-water equations on a twisted icosahedral grid.Part II.A detailed description of the grid and an analysis of numerical accuracy[J].Monthly Weather Review,1995,123(6):1881-1887.

[6] HEIKES R,RANDALL D A.Numerical integration of the shallow-water equations on a twisted icosahedral grid.Part I:Basic design and results of tests[J].Monthly Weather Review,1995,123(6):1862-1880.

[7] GREGORY M J,KIMERLING A J,WHITE D,et al.A comparison of intercell metrics on discrete global grid systems[J].Computers,Environment and Urban Systems,2008,32(3):188-203.

[8] 明涛,庄大方,袁文,等.几种离散格网模型的几何稳定性分析[J].地球信息科学,2007,9(4):40-43.

[9] ZHOU L,LV G.Distortion distribution and convergence analysis of spherical diamond discrete grids[J].ISPRS-International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2013,1(2):89-93.

[10] MING T,ZHANG D,YUAN W.The study on geometrical distortion of triangular partitions in discrete global grid[A].Education Technology and Training,2008 and 2008 International Workshop on Geoscience and Remote Sensing[C].2008,2:175-178.

[11] 赵学胜,孙文彬,陈军.基于QTM的全球离散格网变形分布及收敛分析[J].中国矿业大学学报,2005,34(4):438-442.

[12] KIMERLING J A,SAHR K,WHITE D,et al.Comparing geometrical properties of global grids[J].Cartography and Geographic Information Science,1999,26(4):271-288.

[13] 贲进,童晓冲,张永生,等.球面离散网格在椭球面上的扩展及变形分析[J].测绘科学,2006,31(4):25-27,59.

[14] 孙文彬,赵学胜,高彦丽,等.球面似均匀格网的剖分方法及特征分析[J].地理与地理信息科学,2009,25(1):53-56.

[15] 白建军,孙文彬,赵学胜.基于QTM的WGS84椭球面层次剖分及其特点分析[J].测绘学报,2011,40(2):243-248.

[16] 崔马军,赵学胜.球面退化四叉树格网的剖分及变形分析[J].地理与地理信息科学,2008,23(6):23-25.

[17] WHITE D,KIMERLING A J,SAHR K,et al.Comparing area and shape distortion on polyhedral-based recursive partitions of the sphere[J].International Journal of Geographical Information Science,1998,12(8):805-827.

[18] 赵学胜,王磊,王洪斌,等.全球离散格网的建模方法及基本问题[J].地理与地理信息科学,2012,28(1):29-34.

[19] 赵学胜,侯妙乐,白建军.全球离散格网的空间数字建模[M].北京：测绘出版社,2007.

[20] 李赣华,周东祥,董黎,等.基于Delaunay三角化的有效角点匹配算法[J].信号处理,2007,23(5):695-698.

An Geometry Deformation Evaluation Index of the Spherical Discrete Grid Based on the Fuzzy Similarity

ZHANG Bin,YUAN Zheng-yi,ZHAO Xue-sheng,ZHANG Xin-jian

(CollegeofGeoscienceandSurveyingEngineering,ChinaUniversityofMining&Technology(Beijing),Beijing100083,China)

The uncertainty problem of discrete global grid models,including geometry deformation and spatial distribution,has been one of the restricting factors in its broad applications.In this paper,a fuzzy similarity evaluation index which based on the principle of similar triangles is constructed,and the geometry deformation characteristics and the convergence property of QTM (Quaternary Triangular Mesh) grid are analyzed using the above index.Meanwhile,the location distribution rules of the grid deformation on the octahedral unit and sphere are also presented.Finally,the contrast experiment with the traditional evaluation index (such as the compactness index) is given.The results show that the index not only can reflect the geometry deformation distribution of subdivision models,but also has two advantages just as follows.Firstly,it can reflect both the shape and area deformation of subdivision units,so it can be used as a synthesized evaluable index for the grid′s shape and size.Secondly,the index is an absolute deformation relative to the ideal subdivision units in different recursion levels,and compared with other statistics,it is easier to express the grid geometry deformation in different levels.

discrete global grid system;QTM;geometry deformation of grid;fuzzy similarity

2015-04-20

国家自然科学基金项目(41171306、41171304)

张斌(1990-)，男，硕士研究生，主要研究方向为全球离散格网及三维可视化。E-mail：1289711551@qq.com

10.3969/j.issn.1672-0504.2015.05.005

P208

A

1672-0504(2015)05-0020-05