G′／G展开法在Riccati方程中的应用

魏帅帅，李凯辉，刘汉泽

（聊城大学数学科学学院，山东聊城 252059）

G′／G展开法在Riccati方程中的应用

魏帅帅，李凯辉，刘汉泽

（聊城大学数学科学学院，山东聊城 252059）

通过齐次平衡原理和G′／G展开法对Riccati方程进行求解，得到了满足一定条件的Riccati方程的G′／G解。扩大了对Riccati方程的研究成果，扩展了G′／G展开法的应用。

齐次平衡原理；G′／G展开法；Riccati方程；精确解

0 引言

由于非线性变系数发展方程可以描述许多非均匀介质的物理现象，因此，这些方程的求解近年来得到了人们的广泛关注［1］。非线性变系数发展方程往往比非线性常系数发展方程具有更广泛的物理意义，所以寻求非线性变系数发展方程的解具有重要意义［2］。本文研究如下形式的Riccati方程：

其中：P（x）、Q（x）、R（x）是连续的函数。

Liouville在1841年已经证明：Riccati方程没有初等解法［3］，但是如果能找到Riccati方程的一个特解，再通过初等变换，可求出方程的通解。许多文献对Riccati方程的特解进行了研究［4－5］，但本文并没有从求其特解这方面入手，而是用G′／G展开法［6－17］和齐次平衡原理［18－19］对Riccati方程进行了研究，得到满足一些条件的Riccati方程［20］具有G′／G解，并列举一些特例。然后对一些特例进行了验证，并求出其精确解。

1 Riccati方程G′／G解的存在性

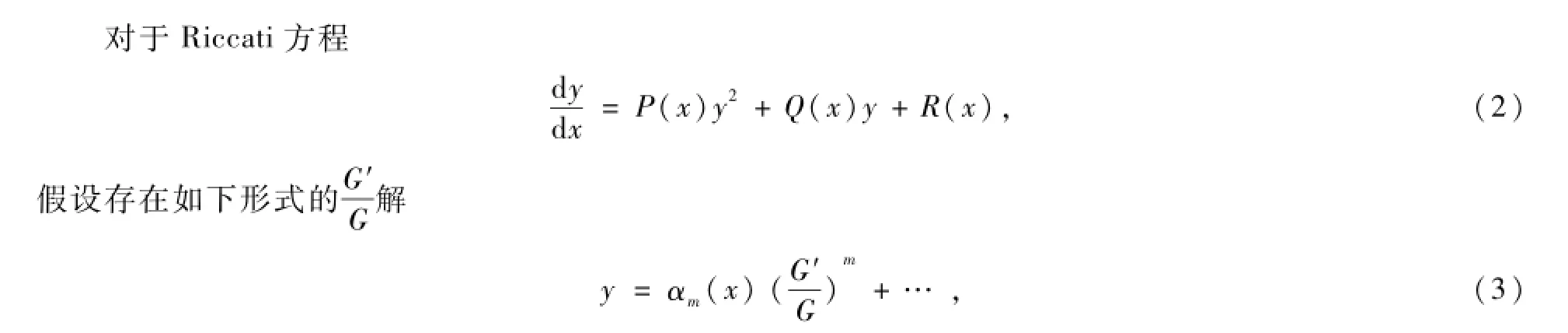
其中：G＝G（x）并且满足二阶线性常微分方程

把式（3）、式（5）和式（6）代入式（2）后，平衡最高阶导数项和最高阶次数项得到m＝1。那么，可设

2 求解举例

对于上面列举的一些例子，下面针对其中2个求出其精确解，具体过程如下。

例1如下方程：

把式（4）、式（19）和式（20）代入式（18）可以得到如下形式的解：

其中：C1和C2是任意的常数。

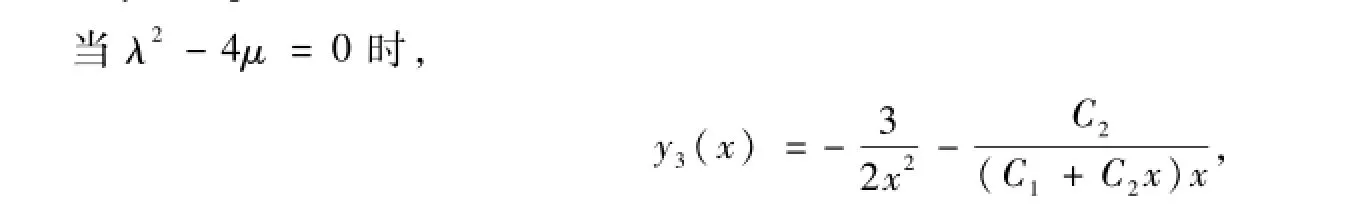
其中：C1和C2是任意的常数。

3 结论

开法求解有很大的便利性和发展前景。利用Lie群分析，可以将非线性发展方程约化为常微分方程，其中有些约化方程即为Riccati方程，这样，利用本文的方法，可以求出某些Riccati方程的解，从而得到非线性发展方程的解。因此，本文的方法在求解非线性发展方程中也起着重要的作用。

［1］ 刘睿.相容性方法在求解变系数发展方程中的应用［J］.河北师范大学学报：自然科学版，2011，35（5）：442－447.

［2］ 王岗伟，刘希强，张颖元.变系数mKdV方程的精确解［J］.井冈山大学学报：自然科学版，2012，33（5）：1－5.

［3］ 王高雄，周之銘.常微分方程［M］.3版.北京：高等教育出版社，2006.

［4］ 杜炜，师建国.Riccati方程的特解［J］.天中学刊，2003，18（5）：6－7.

［5］ 王建明.Riccati微分方程特解新求法的研究［J］.数学的实践与认识，2006，36（7）：382－386.

［6］ Wang M L，Li X Z，Zhang J L.The（G′／G）-expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics［J］.Physics Letters A，2008，372（4）：417－423.

［7］ 李帮庆，马玉兰.（G′／G）展开法和（2＋1）维非对称Nizhnik-Novikov-Veselov系统的新精确解［J］.物理学报，2009（7）：4373－4378.

［8］ 郭冠平，周国中，何宝钢.G′／G展开法对非线性耦合Klein-Gordon方程组的精确解磁［J］.浙江师范大学学报：自然科学版，2010，33（3）：286－290.

［9］ 牛艳霞，李二强，张金良.利用（G′／G）-展开法求解2＋1维破裂孤子方程组［J］.河南科技大学学报：自然科学版，2008，29（5）：73－76.

［10］ 施业琼.应用（G′／G）-展开法求解高阶非线性薛定谔方程［J］.广西工学院学报，2009，20（3）：45－49.

［11］ 张国栋，秦清锋.齐次平衡法在微分方程中的应用［J］.中国新技术新产品，2010（21）：243－244.

［12］ 李保安，李灵晓.（G′／G，1／G）-展开法在求解非线性演化方程中的应用［J］.河南科技大学学报：自然科学版，2015，36（3）：90－95.

［13］ 施业琼.（2＋1）维Davey-StewartsonⅡ方程的精确解［J］.广西科技大学学报，2015，26（1）：96－102.

［14］ 赵烨，徐茜.一类耦合Benjamin-Bona-Mahony型方程组的新精确解［J］.纯粹数学与应用数学，2015，31（1）：12－17.

［15］ 孔淑霞.应用（G′／G）展开法求非线性弦振动方程的精确解［J］.高师理科学刊，2014，34（3）：10－12.

［16］ 李保安，李灵晓.简化变形Ostrovsky方程的精确解［J］.河南科技大学学报：自然科学版，2014，35（2）：82－85.

［17］ 李向正.Sawada-Kotera方程的两类尖孤立波解［J］.河南科技大学学报：自然科学版，2014，35（2）：78－81.

［18］ 张辉群.齐次平衡方法的扩展及应用［J］.数学物理学报，2001，21（3）：321－325.

［19］ 刘式适，傅遵涛，刘式达，等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用［J］.物理学报，2001，50（11）：2068－2073.

［20］ Liu H Z，Li J B，Liu L，et al.Group Classifications，Optimal Systems and Exact Solutions to the Generalized Thomas Equations［J］.Journal of Mathematical Analysis and App lications，2011，383（2）：400－408.

O175.2

A

1672－6871（2015）05－0092－05

国家自然科学基金项目（11171041）

魏帅帅（1991－），男，山东济宁人，硕士生；刘汉泽（1962－），男，山东滨州人，教授，博士，硕士生导师，研究方向为微分方程理论与应用.

2015－03－25