砖孔内贴保温层对空心砖外墙保温性能的影响
刘峪良,李临平,王 飞,陶文铨,何雅玲
(1.太原理工大学环境科学与工程学院,山西太原 030024;2.西安交通大学能源与动力工程学院,陕西西安 710049)
砖孔内贴保温层对空心砖外墙保温性能的影响
刘峪良1,李临平1,王 飞1,陶文铨2,何雅玲2
(1.太原理工大学环境科学与工程学院,山西太原 030024;2.西安交通大学能源与动力工程学院,陕西西安 710049)
针对提高空心砖外墙保温性能有利于降低建筑能耗的问题,本文采用有限容积法,研究了空心砖孔内贴10 mm保温层对建筑外墙保温性能的影响,并进行了三维复合传热的数值模拟分析。文中选取12种具有不同孔洞数和排列方式的240 mm×115 mm×90 mm空心砖、4种不同导热系数的保温材料、两种厚度的空心砖外墙(24墙和37墙)作为研究对象。研究结果表明:砖孔内贴保温层可以有效提高墙体保温性能,24墙的墙体保温性能提高19.1%~59.3%,37墙的墙体保温性能提高16.9%~58.3%,尤其对于开孔率较大的砖型,采用该方法节能效果显著。
空心砖;保温材料;当量导热系数;数值模拟
0 引言
随着人们生活水平的提高,每年大量能源用于室内采暖和供冷以满足人们对室内舒适性的要求。据统计,中国建筑能耗约占到全国总能耗的30%,参照发达国家的发展历程,这个比例将逐步提高到40%左右。暖通空调能耗是建筑能耗的重要组成部分,由于化石能源日渐枯竭及可持续发展要求,建筑节能已经成为全球共识。空心砖由于其良好的热工性能和质轻等特点,在中国广泛用于砌筑建筑外墙。近10年来,国内外对于改善空心砖外墙的保温性能做了大量研究。文献[1]借助数值模拟和实验方法探究了砖孔填充膨胀珍珠岩对空心砖保温性能的影响。文献[2]研究了内插阻隔板将单个方形砖孔分割成多个三角形砖孔对空心砖当量导热系数的影响,研究结果表明:采用该方法可以有效提高空心砖的保温性能达37%~42%。文献[3-6]采用有限元法对空心砖传热性能的优化做了大量三维数值研究。文献[7-8]借助有限容积法分别对两种空心砖(240 mm×115 mm×90 mm和290 mm×140 mm×90 mm)进行了砖孔结构的优化,得到了最佳砖型。文献[9]采用有限容积法研究了外贴50 mm保温层对空心砖外墙保温性能的影响。然而,目前文献中关于砖孔内贴保温层对空心砖外墙保温性能影响这方面的研究很少。鉴于此,本文基于有限容积法,采用能够同时处理导热、对流、辐射传热的三维耦合程序(用Fortran语言编制),分别研究了砖孔内贴10 mm保温层在4种不同导热系数下,对两种空心砖外墙(24墙和37墙)传热性能的影响。
1 物理问题和数学模型
图1表示的是24墙最小的数值计算区域,由4块相同的空心砖经砂浆砌合而成,各砖孔表面贴有10 mm保温层。6块相同的空心砖组成的37墙计算模型如图2所示。文中采用LC1WC2HC3表示不同砖孔数目的砖型(该空心砖长度方向有C1个孔,宽度方向C2个孔,高度方向C3个孔)。本文选取了12种砖型、4种不同导热系数的保温材料和两种砌筑方式的外墙作为研究对象,数值模拟中,空心砖外墙内外表面为对流换热边界条件,其他4面为绝热边界条件。
根据物理过程的特点,数值模拟中采用如下假设:(1)空心砖、砂浆、保温层所用材料和砖孔内空气的热物性参数为常数;(2)砖孔内的空气不参与气体辐射,流动状态为不可压缩、稳态、层流流动;(3)Boussinesq假设适用。
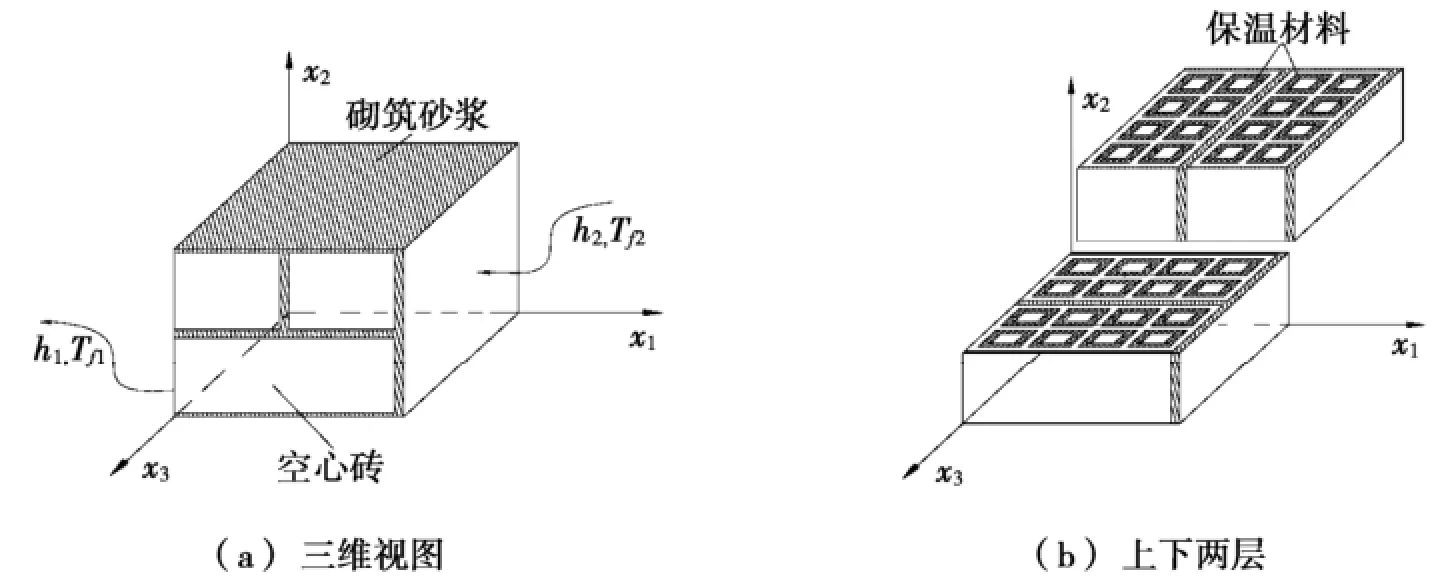
图1 24墙计算区域
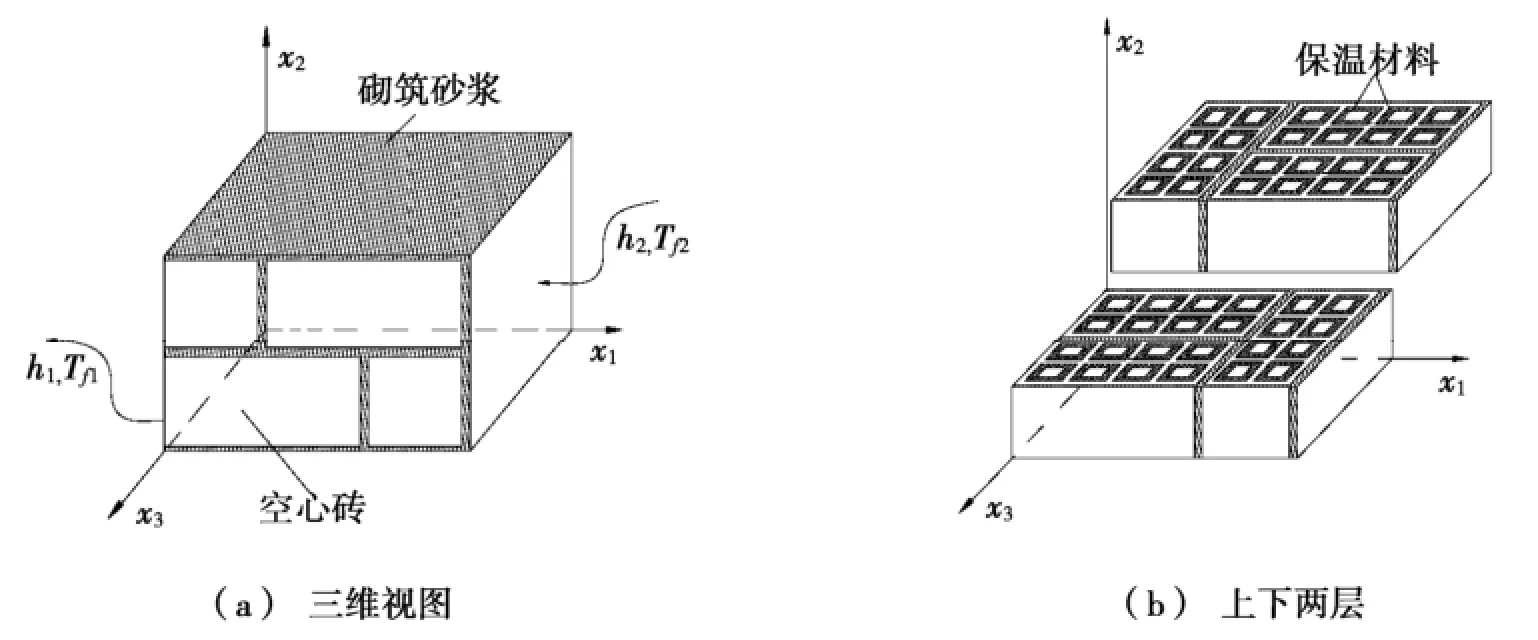
图2 37墙计算区域
1.1 物理模型的控制方程及边界条件式中:u1、u2、u3分别为x1、x2、x3方向的速度;s1、s2、s3分别为x1、x2、x3方向动量方程的源项;β为空气的体膨胀系数;L、H、W表示计算区域在x1、x2、x3方向的长度;h1、h2分别表示计算区域外表面和内表面对流换热表面传热系数;Tf1、Tf2分别表示室外、室内设计温度;Tin、Tout分别表示室内、室外墙壁表面温度;λs为空心砖材料的导热系数;λss为内抹灰的导热系数;数值模拟中用到的热物性参数见表1。


表1 热物性参数
1.2 导热系数求解
从图1和图2可以看出:通过计算区域的传热量分为3部分:室内空气以对流换热的方式将热量传入计算区域的内表面;传入计算区域内表面的热量,通过空心砖内复杂的传热过程传到计算区域的外表面;室外空气又以对流换热的方式将传到计算区域的外表面热量传出。根据热平衡原理,这3部分的传热量应相等,即
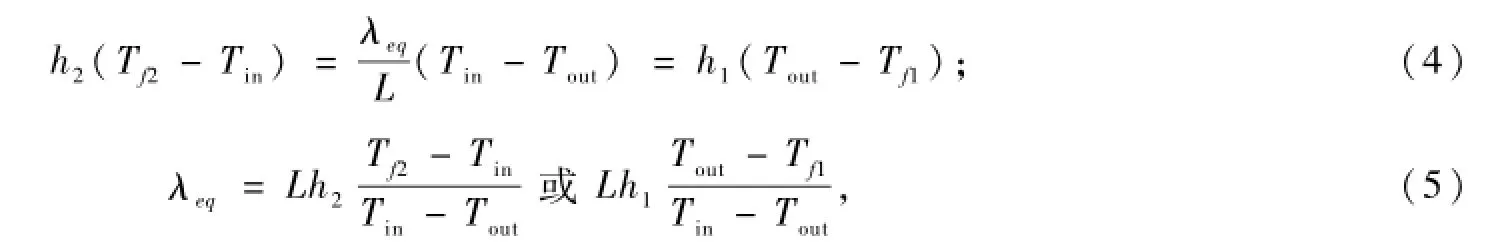
式中:λeq为空心砖外墙的当量导热系数,W/(m·K)。
1.3 辐射换热的处理
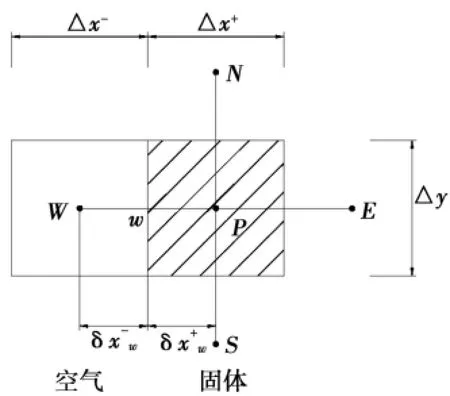
图3 W界面两侧的控制容积
由于砖孔各内表面温度不同,每个表面与其他表面之间必然存在辐射换热,求解空心砖墙当量导热系数时不能忽略空气孔辐射换热的影响。本文采用附加源项法处理辐射换热[10],以图3为例。

式中:Sc,ad,air为空气侧控制容积的附加源项;Sc,ad,solid为固体侧控制容积的附加源项;qrad为净辐射热流,J(n)为有效辐射量,可按下式求取:
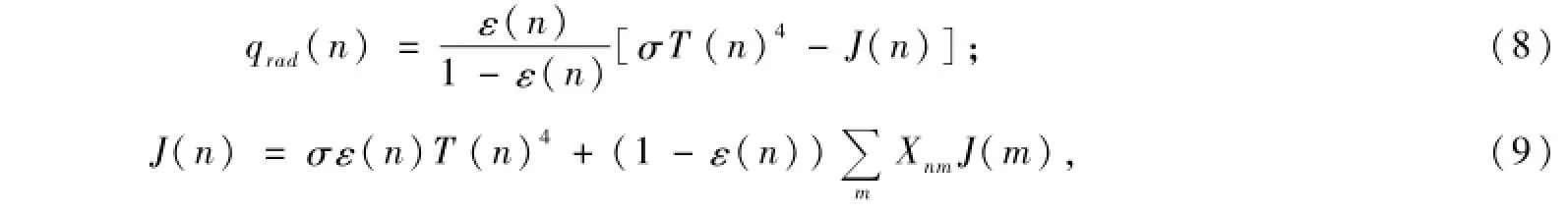
其中:n=1,2,3,4,5, 6;m=1,2,3,4,5,6,分别表示空气孔的6个内表面;Xnm为空气孔各表面角系数。
1.4 主要数值计算方法及收敛判据
本文利用有限容积法对微分方程进行离散,对流项的离散格式采用绝对稳定的具有二阶精度的差分格式(SGSD)[11],离散的代数方程采用三对角阵算法及交替方向隐式线迭代法(TDMA+ADI)进行整场变量求解[10],压力与速度耦合关系处理采用对压力方程进行两次内迭代的高效算法(IDEAL)[12]。
本文采用的迭代收敛判据为:
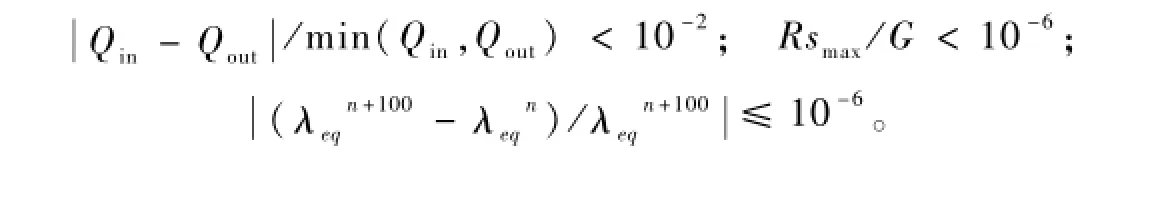
2 计算结果与分析
2.1 砖孔内贴保温层对24墙保温性能的影响
4种不同导热系数λb的保温材料,内贴保温层厚度为10 mm,在相同的条件下数值模拟结果见表2和图4。当宽度方向孔洞数目固定时,空心砖外墙当量导热系数随长度方向孔洞数目的变化规律基本一致。数值模拟结果显示:采用该方法可以显著提高墙体的保温性能达19.1%~59.3%,尤其对于开孔率大的砖型节能效果更加明显。
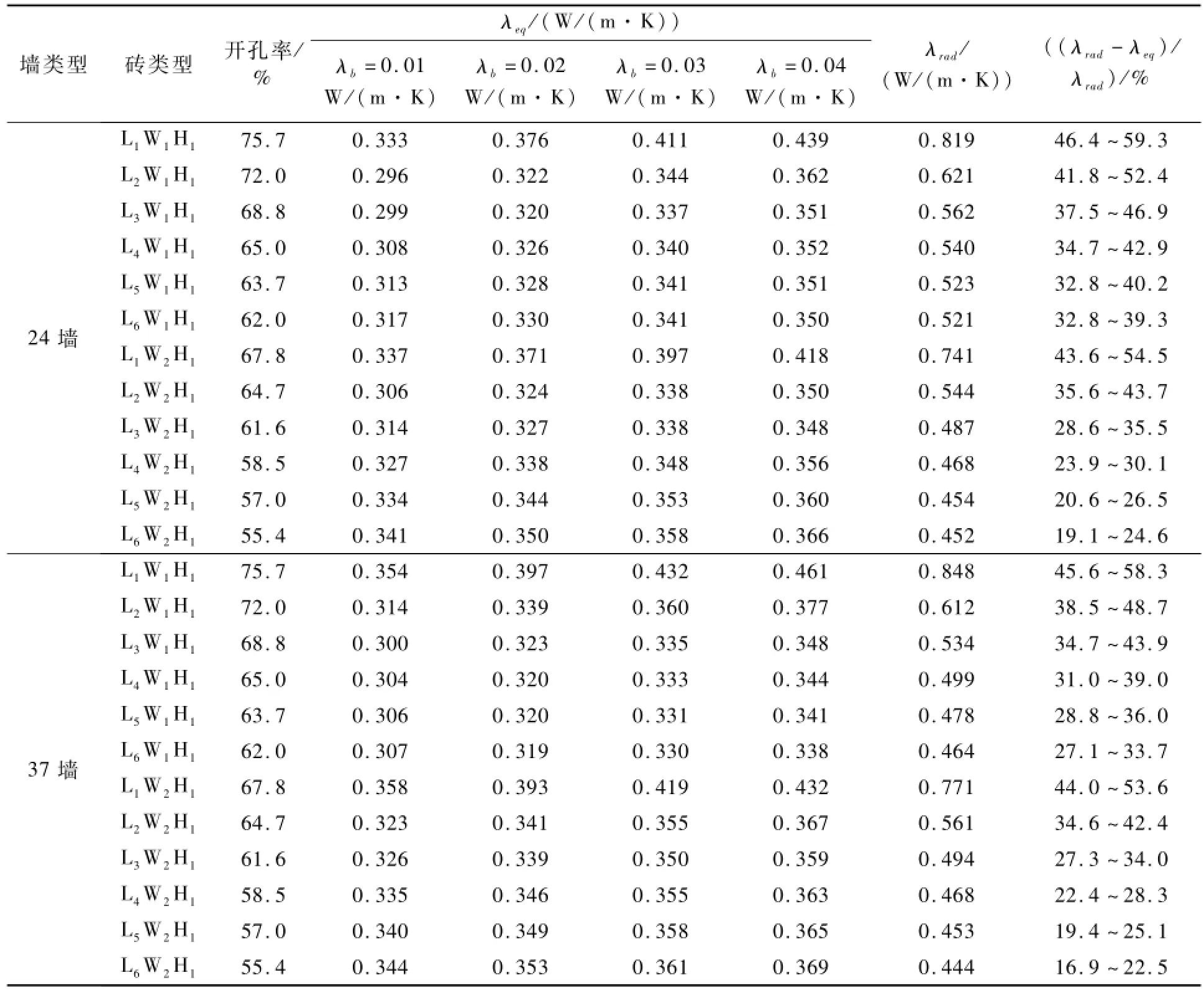
表2 24墙和37墙模拟结果
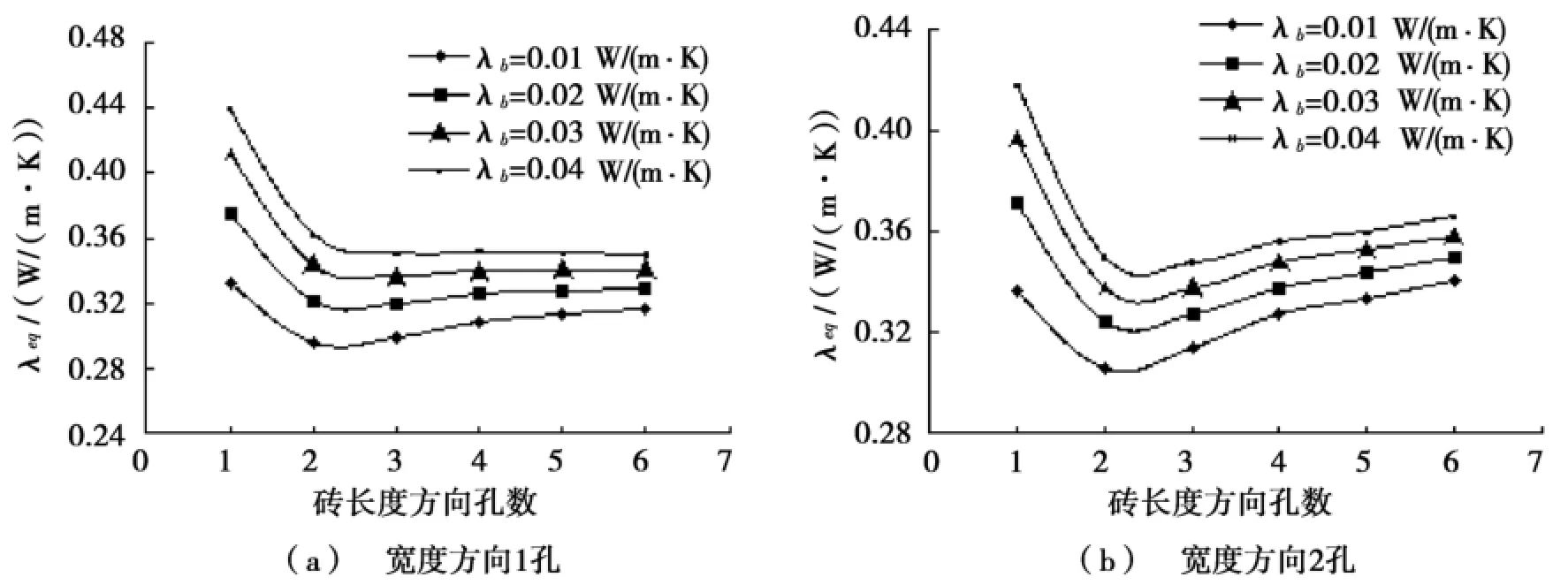
图4 24墙的当量导热系数随孔洞数的变化
以L1W1H1为例,采用4种不同导热系数λb的保温材料,空心砖墙保温性能的相对变化率为46.4%~59.3%,然而随着孔洞数目的增加,其相对变化率逐步减少。选用低导热系数保温材料对空心砖墙保温性能的强化效果越来越弱,对于L6W2H1来说,相对变化率差值仅为5.5%。
2.2 砖孔内贴保温层对37墙保温性能的影响
本节选取37墙作为研究对象,采用与上节相同的条件进行数值模拟,结果如表2和图5所示。与24墙对比可以发现:当宽度方向孔洞数一定时,两种外墙的当量导热系数随砖孔长度方向孔洞数的变化规律基本一致。对于37墙来说,采用该方法墙体的保温性能提高了16.9%~58.3%,对于开孔率大的砖型节能效果同样适用。以L1W1H1为例,采用4种不同导热系数λb的保温材料,空心砖墙保温性能的相对变化率为45.6%~58.3%。比较表2可以发现:当长度方向孔洞数目为1时,除L1W1H1和L2W1H1外,37墙的保温性能优于24墙,采用该方法可以得到更低的当量导热系数;然而,当宽度方向孔洞数为2时,情况恰好相反,24墙的保温性能反而优于37墙。从图5b可以发现:当宽度方向孔洞数目为1时,在所研究的保温材料所取导热系数范围内,空心砖墙的当量导热系数随长度方向孔洞数目的增加而减少,但减少的幅度趋于平缓;当宽度方向孔洞数目为2,空心砖墙的当量导热系数呈现先急剧降低,然后缓慢上升,对于每一种工况,都在长度方向孔洞数目为2时取得最小值。出现这种现象是因为当宽度方向的孔洞数给定时,随着长度方向的孔洞数的增加,孔内辐射换热量和自然对流换热量减少,但导热热量增加,当孔内辐射换热量和自然对流换热量减少的程度大于导热热量增加的程度时,空心砖墙的当量导热系数呈下降的趋势,反之则上升。

图5 37墙的当量导热系数随孔洞数的变化
2.3 两种典型砖型的温度速度场分布图
选取两种典型的砖型L1W1H1和L6W2H1作为分析对象,空气孔内贴10 mm保温层前后温度场见图6和图7。图6和图7分别给出砖型L1W1H1和L6W2H1在截面x3=0.03处的温度分布。两种比较可以发现:内贴保温层可以显著抑制空气孔内部的对流和辐射换热强度。随着砖型孔洞数目的增大,导热所占的比重越来越大,如图7b所示,温度场内各等温线几乎是平行的直线。
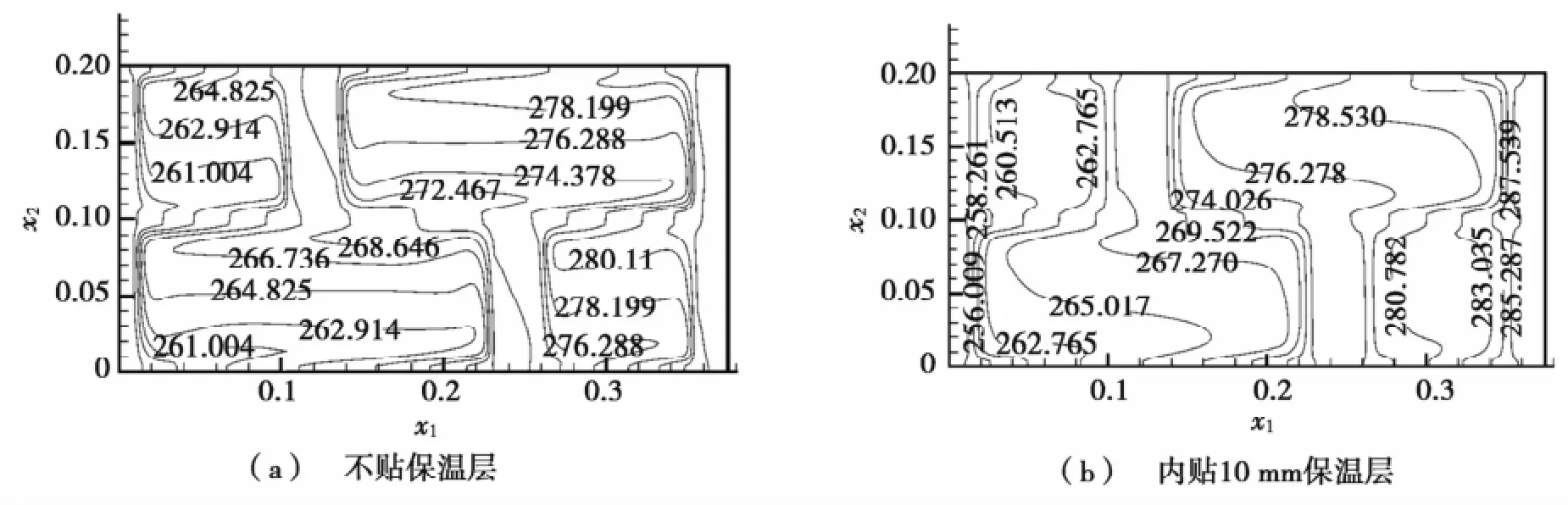
图6 L1W1H1空心砖墙的温度分布(x3=0.03断面)
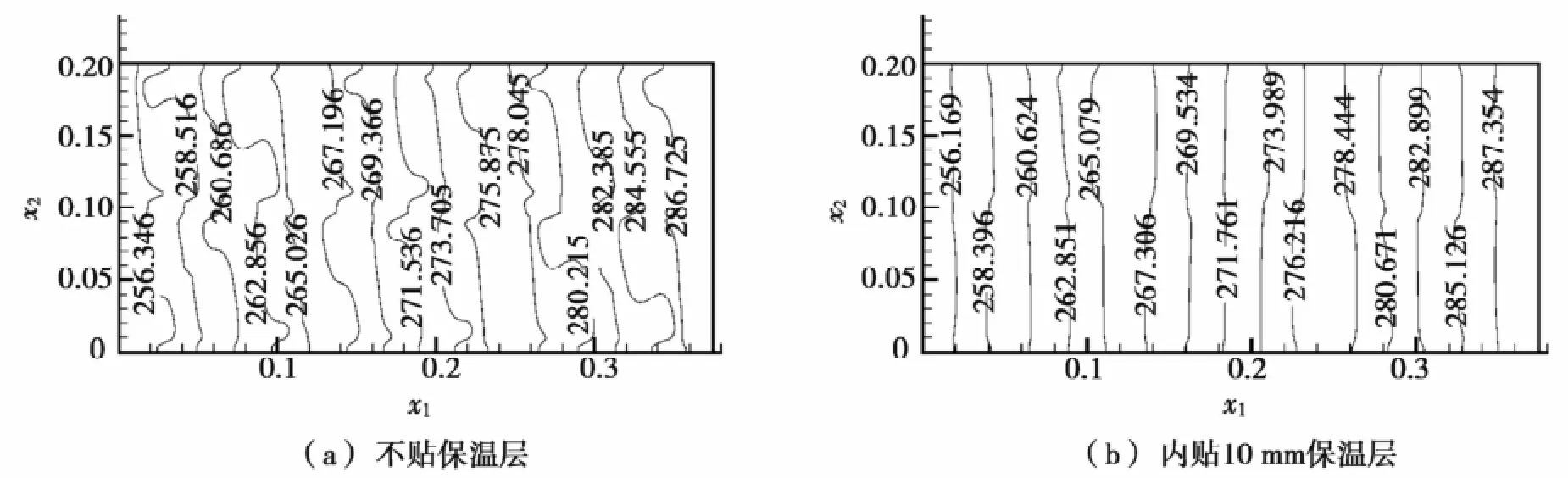
图7 L6W2H1空心砖墙的温度分布(x3=0.03断面)
3 结论
本文采用自编三维程序,研究了砖孔内贴10 mm保温层在4种不同导热系数下,对两种空心砖外墙保温性能的影响进行了数值分析。主要结论如下:
(1)砖孔内贴10 mm保温层可以有效提高空心砖墙体的保温性能,尤其对于开孔率大的砖型,如L1W1H1、L2W1H1、L3W1H1和L1W2H1。对24墙,墙体保温性能提高了19.1%~59.3%;37墙可以提高16.9%~58.3%。
(2)空心砖选用低导热系数的保温材料可以得到更好的保温效果,如L1W1H1砌筑的24墙,当保温材料的导热系数从0.040 W/(m·K)变化到0.010 W/(m·K)时,墙体的当量导热系数从0.439 W/(m·K)降低到0.333 W/(m·K),保温效果从46.4%变化到59.3%,增加了12.9%。随着砖型孔洞数增加及开孔率的减小,保温效果提高的幅度逐渐变小,如L6W2H1砌筑的24墙,在相同的保温材料导热系数的变化范围内,墙体的当量导热系数从0.366 W/(m·K)降低到0.341 W/(m·K),保温效果从19.1%变化到24.6%,仅增加了5.5%。
(3)对于宽度方向为1孔的砖型,L1W1H1和L2W1H1除外,采用该方法37墙的当量导热系数比24墙低。然而,当宽度方向孔洞数为2时,24墙的当量导热系数反而低于37墙。
[1] Zukowski M,Haese G.Experimental and Numerical Investigation of a Hollow Brick Filled with Perlite Insulation[J]. Energy and Buildings,2010,42(9):1402-1408.
[2] Alhazmy M M.Numerical Investigation on Using Inclined Partitions to Reduce Natural Convection Inside the Cavities of Hollow Bricks[J].International Journal of Thermal Sciences,2010,49(11):2201-2210.
[3] Del C D J J,García N P J,Martín A,et al.Non-linear Thermal Analysis of Light Concrete Hollow Brick Walls by the Finite Element Method and Experimental Validation[J].Applied Thermal Engineering,2006,26(8):777-786.
[4] Del C D J J,García N P J,Suárez S J L,et al.Nonlinear Thermal Optimization of External Light Concrete Multi-enclosured Brick Walls by the Finite Element Method[J].International Journal of Heat and Mass Transfer,2008,51(7):1530-1541.
[5] Del C D J J,García N P J,Alvarez R F P,et al.Non-linear Thermal Analysis of the Efficiency of Light Concrete Multiholed Bricks with Large Recesses by FEM[J].Applied Mathematics and Computation,2012,218(20):10040-10049.
[6] Del C D J J,García N P J,Alvarez R F P,et al.The Use of Response Surface Methodology to Improve the Thermal Transm ittance of Lightweight Concrete Hollow Bricks by FEM[J].Construction Building Material,2014,52:331-44.
[7] Li L P,Wu Z G,Li Z Y,et al.Numerical Thermal Optimization of the Configuration of Multi-holed Clay Bricks Used for Constructing Building Walls by the Finite Volume Method[J].International Journal of Heat and Mass Transfer,2008,51(13):3669-3682.
[8] Li L P,Wu Z G,Li Z Y,et al.Optimization of the Configuration of 290×40×90 Hollow Clay Bricks with 3-D Numerical Simulation by Finite Volume Method[J].Energy and Buildings,2008,40(10):1790-1799.
[9] 马静,李临平,陶文铨,等.保温层对空心砖当量导热系数影响的数值研究[J].工程热物理学报,2012,33(11):1947-1949.
[10] 陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.
[11] Li Z Y,Tao W Q.A New Stability-guaranteed Second-order Difference Scheme[J].Numerical Heat Transfer:Part B,2002,42(4):349-365.
[12] 孙东亮,屈治国,何雅玲,等.求解流动与传热问题的一种高效稳定的分离式算法—IDEAL[J].工程热物理学报,2009,30(8):1369-1372.
TK124
A
1672-6871(2015)05-0030-06
山西省自然科学基金项目(2014011033-2)
刘峪良(1991-),男,山西运城人,硕士生;李临平(1957-),女,通信作者,山西太原人,副教授,博士,硕士生导师,主要从事空心砖外墙传热传质学方面的研究.
2015-01-19

