滚石冲击下孔隙率和孔隙分布对空心砖缓冲性能的影响

邵国建，刘超福，苏宇宸，吕亚茹

(河海大学力学与材料学院，江苏 南京 211100)

滚石灾害作为三大山区地质灾害之一，严重地威胁着山区人民的生命财产安全和建筑物安全[1-3]。挡土墙作为防止土体坍塌的永久或临时性建筑物, 广泛应用于土木建筑、水利水电、铁道桥梁、水土保持和矿山坑道等工程中[4]。为了预防滚石灾害造成的损失，通常会在滚石预测路径上设置挡板、拦石墙等刚性拦挡结构，并在拦挡结构之前安装缓冲垫层来削减滚石的冲击力和吸收滚石的冲击能量。因此，垫层材料的选择是滚石灾害防护能否成功的关键之一。砂石材料是滚石灾害防护中最常见的垫层材料[5-6]，但是在一些场合如陡峭的山坡上，由于砂石材料的运输、安装等难度较大，损坏后的维护、更换也较为困难，因此砂石材料并非总是最优的选择。为此，国内外许多学者为探寻新型垫层材料展开了大量的冲击试验和数值模拟研究。

邓力源等[7]利用ANSYS/LS-DYNA软件建立轮胎有限元模型，研究了废旧轮胎在新型柔性拦石墙中的应用，结果表明废旧轮胎吸能作用明显,能够有效减缓落石对刚性拦石墙的冲击,并显著提高新型柔性拦石墙的防护能力。Ng等[8]针对泡沫玻璃开展了现场冲击试验，结果表明泡沫玻璃破碎强度较低，在滚石冲击下大量泡沫玻璃破碎，相比传统碎石垫层对冲击力的削减提高了25%，说明低强度的泡沫玻璃材料可有效提高垫层材料缓冲性能。余跃[9]利用ANSYS/LS-DYNA软件建立了基于弹-塑性响应的新型材料泡沫铝结构的数值模型，模拟分析了该结构在冲击载荷下变形量最小即抵抗结构变形能力最强时的相对密度分布情况。Peila等[10]通过足尺试验对高塑性黏土拦石墙进行了研究，并与传统防护拦石墙进行了对比验证。Pohrt等[11]调查了用混凝土填充管状钢梁(CFT)建造的落石防护装置，结果表明CFT结构在冲击荷载作用下具有很大的变形和能量吸收能力。魏培勇等[12]研究了碾压混凝土动态力学特性，预测了真实应变率效应对碾压混凝土结构在冲击荷载下的动态响应。Renato等[13]为防岩石坠落设计了钢混凝土复合结构，该结构具有高抗冲击能力和延展性，保持的抗冲击安全边际大于RC/PC结构。王东坡等[14-16]对滚石冲击泡沫铝夹芯板动力响应以及EPS垫层棚洞的耗能机理进行了分析。方有珍等[17]研究了新型卷边PEC柱-钢梁组合框架抗震性能，从试件的承载力、刚度衰减规律、自复位功效、耗能能力和节点传力机理等方面分析了试件的抗震机理。Lam 等[18]、Su 等[19]分别针对EVA 泡沫和泡沫混凝土等新型垫层材料开展了冲击试验和数值模拟研究，试验结果均表明冲击荷载下泡沫结构内部孔洞的严重垮塌可耗散大量滚石冲击能，进而有效削减滚石冲击力。可见多孔隙、破碎强度低的垫层材料具有更好的缓冲性能。

本文基于空心砖多孔隙、易破碎、 高耗能、易安装等特点，采用大型摆锤冲击试验和LS-DYNA数值模型研究空心砖孔隙率和孔隙分布对其缓冲特性的影响。

1 试验装置和试验方法

现场试验装置如图1所示，采用摆锤冲击装置模拟滚石冲击。摆锤冲击装置主要由落石运动装置、缓冲垫层与刚性拦挡结构、数据采集装置3部分组成。

图1 摆锤冲击装置Fig.1 Pendulum impact device

落石运动装置由尺寸为3 m×5 m×6 m的立体钢架、混凝土球以及钢绞线组成。钢架固定在地面上，混凝土球质量为2 000 kg,直径为1.16 m，用吊车将混凝土球向后拉升到设定的高度以获得20 kJ的冲击能量，由释放装置控制其释放。缓冲垫层与刚性拦挡结构由空心砖缓冲层与钢筋混凝土挡墙两部分组成。空心砖缓冲层由尺寸为0.39 m×0.19 m×0.19 m、密度为2 000 kg/m3的2孔空心砖(图2)砌成，宽3 m、高3 m、厚0.4 m。钢筋混凝土挡墙为宽3 m、高3 m、厚1.5 m的墙体。在钢筋混凝土挡墙上安装8个测压元件(图3)，以测量缓冲层水平和垂直方向传递力分布，其中测压元件的测压面积为15×15 cm2,其分布如图2所示。安装压阻式加速度计(1B107)来测量混凝土球的加速度时程，滚石冲击力用测得的混凝土球加速度与混凝土球质量的乘积表示。侵彻深度时程曲线由摆锤冲击垫层的开始时刻到结束时刻之间的加速度时程二次积分得到。基于计算机数据采集系统以10 kHz的采样率记录数据。

图2 空心砖Fig.2 Hollow brick

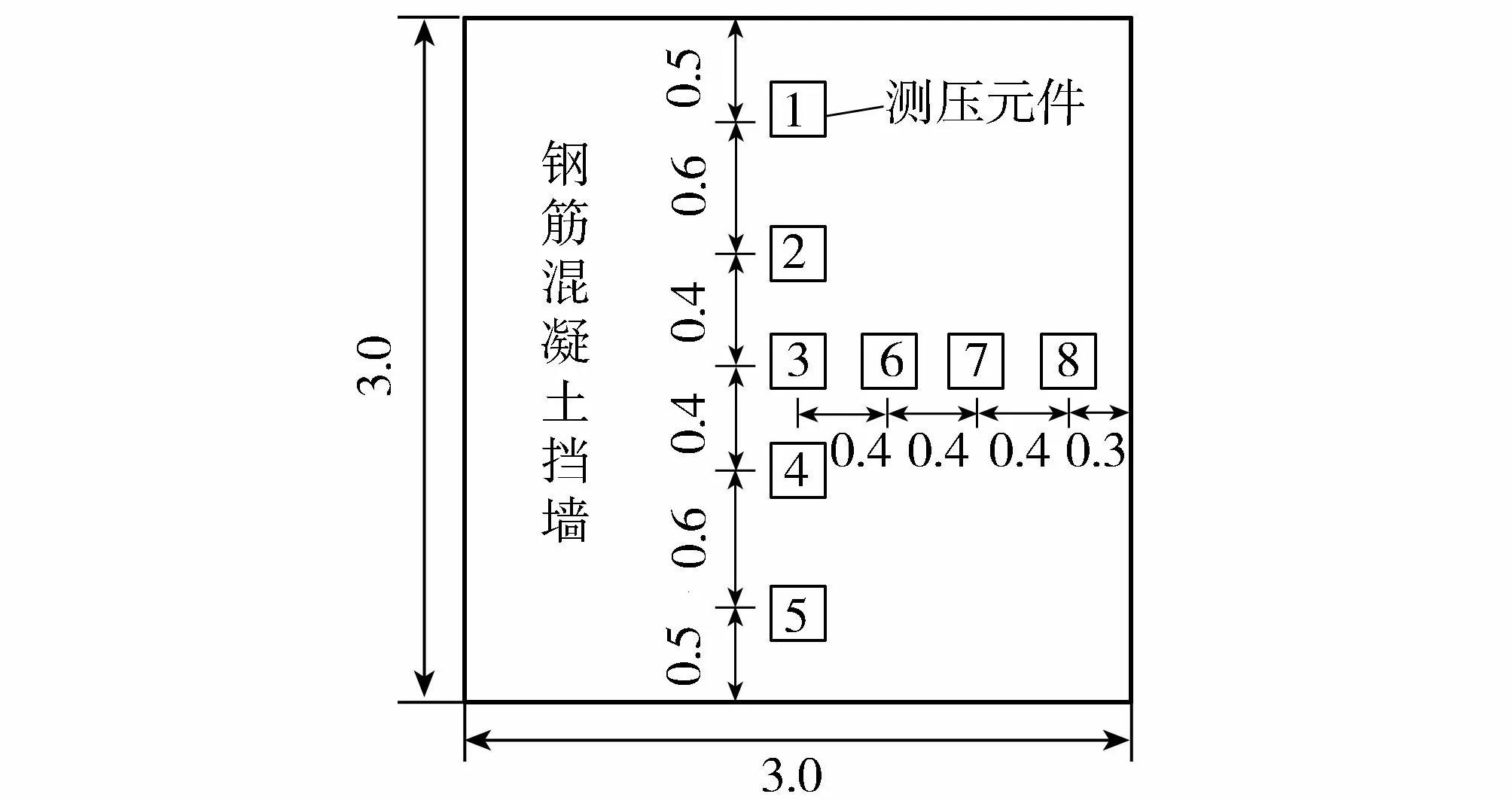
图3 测压元件布置(单位：m)Fig.3 Load cell layout (unit: m)

2 有限元数值模型的建立与验证

采用LS-DYNA显示动力分析程序进行20kJ冲击能量滚石冲击空心砖缓冲层的三维有限元模拟。

基于LS-DYNA建立了与现场试验相同尺寸的数值模型(图4)，几何模型采用AutoCAD软件建模, 然后导入Hypermesh软件进行网格划分，使用LS-PrePost做前处理，最后导入LS-DYNA有限元软件进行分析。其中，钢筋混凝土挡墙及空心砖缓冲层材料模型采用159号混凝土材料模型(MAT_CSCM_CONCRETE), 密度取为实际空心砖的密度(2 000 kg/m3)，单元为六面体Solid164实体单元，单元数分别为72 000和468 000。混凝土球材料模型采用刚体材料模型(MAT_RIGID)，即假定其不发生变形，采用四面体Shell163壳单元减少单元数目以提高计算效率。由于重力远小于冲击力，并且冲击过程持续时间短暂，因此不考虑重力的影响。数值模型滚石初始速度设为4.5 m/s(冲击能量为20kJ)。数值模型无侧限抗压强度由现场试验结果得到。考虑混凝土材料模型应变率的影响，连续帽盖模型参数irate设为1，ERODE侵蚀破坏参数设为1.25，最大骨料粒径为0.015 m，单位选项为UINT，当采用国际单位制时数值为4，其余参数(如泊松比等)均可采用默认值或由程序自行算出。钢筋混凝土挡墙模型的密度及骨料粒径取为现场试验相同的数值，其余计算参数与空心砖模型的计算参数一致。约束钢筋混凝土挡墙上、下、左、右4个面的x、y、z方向上的位移。空心砖之间采用共用节点的方式定义接触，不考虑黏结滑移。采用自动单面接触定义滚石曲面与空心砖缓冲层表面接触。

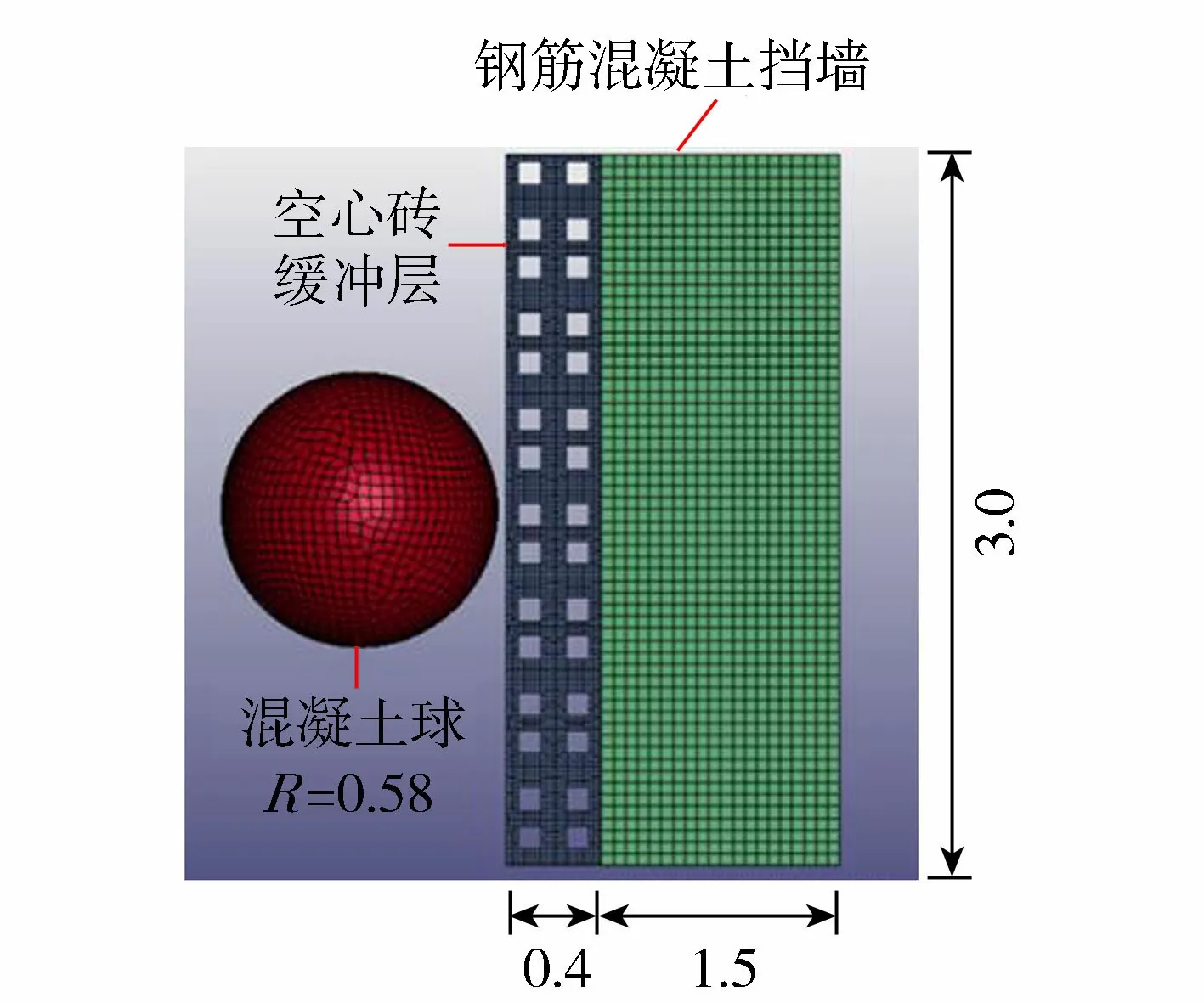
图4 数值模型(单位：m)Fig.4 Numerical model (unit: m)

图5给出了在20 kJ滚石冲击能量下，数值模拟与现场试验的滚石冲击力-位移曲线，两者吻合程度较高，现场试验滚石冲击力峰值为908kN，数值模拟滚石冲击力峰值为808 kN，误差为11.2%，这是由于现场试验中破碎的砖块会被混凝土球压缩密实，而数值模拟中缓冲层的侵彻部分由删除单元承担，由此导致数值模拟中的滚石冲击力略小于现场试验中的滚石冲击力。通过对滚石冲击力-位移曲线积分得到缓冲垫层耗散的总能量，其中现场试验中缓冲层耗散的能量为19.1 kJ，数值模拟中缓冲层耗散的能量为20.0 kJ，二者误差不到5%，误差的原因是现场试验中存在摩擦力和钢绞线拉力对混凝土球做负功，使得混凝土球的实际冲击能量减小。此外数值模拟的冲击时间与现场试验冲击时间十分接近，分别为0.023 s和0.024 s，误差仅为4%。数值模拟曲线与试验曲线吻合较好，可以认为数值模型能够准确地模拟滚石冲击试验。

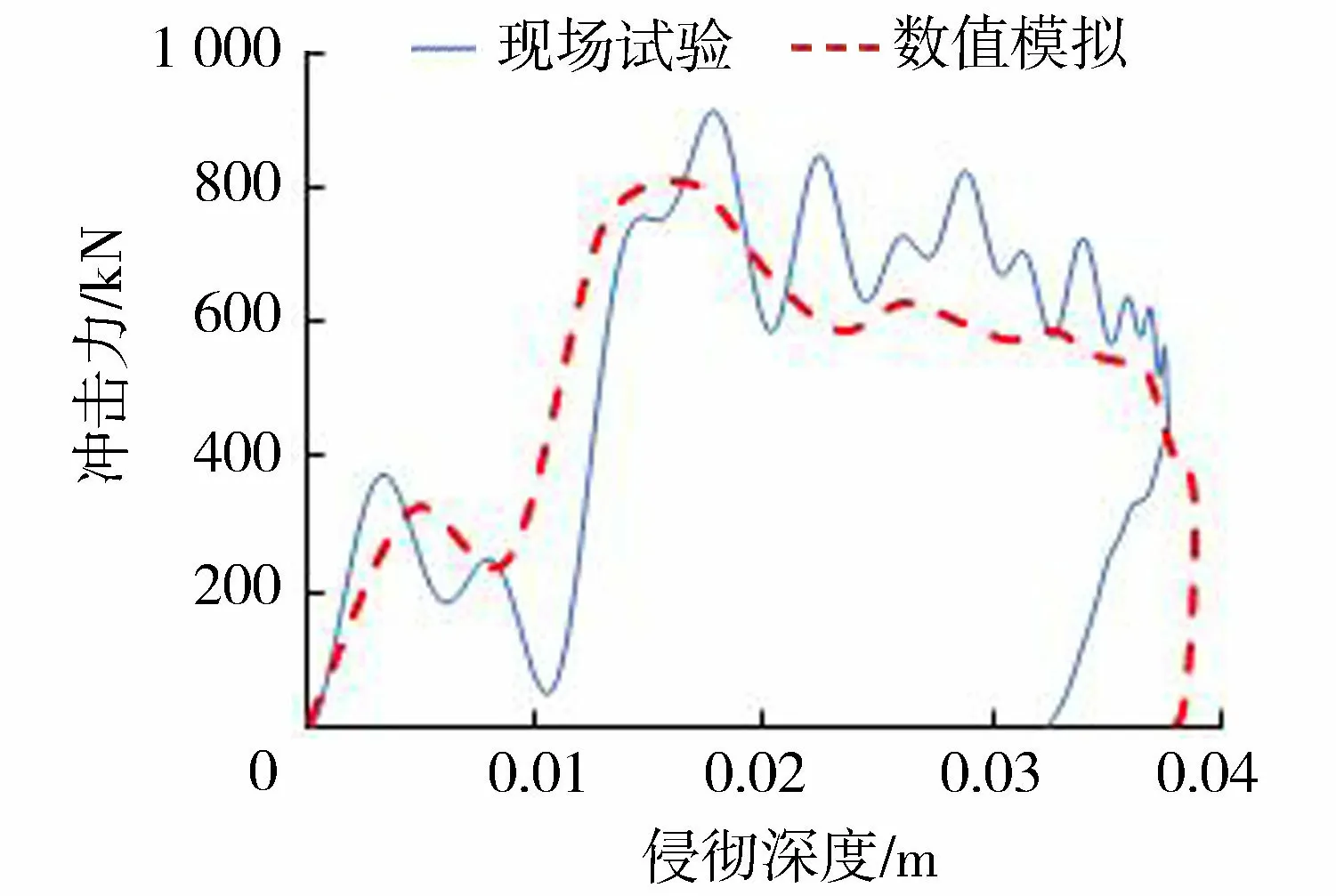
图5 滚石冲击力-位移曲线Fig.5 Impact force-displacement curve of rolling rock

图6给出了空心砖缓冲层的水平方向和垂直方向的传递力分布。图6(a)中横坐标表示的是水平方向上的4个测压元件(标号为3、6、7、8)的水平距离，纵坐标为对应测压元件接收的传递力峰值；图6(b)中纵坐标表示的是垂直方向上的5个测压元件(标号为1、2、3、4、5)的垂直高度，横坐标为对应测压元件接收的传递力峰值。可以看出，现场试验与数值模拟的垫层传递力分布也较为一致，最大垫层传递力都出现在垫层中心点3号测压元件处，传递力由中心点径向往外急剧减小，其中误差最大处仅为15%，证明数值模型能够较为可靠地反映出试验时混凝土球冲击空心砖缓冲层的冲击响应。

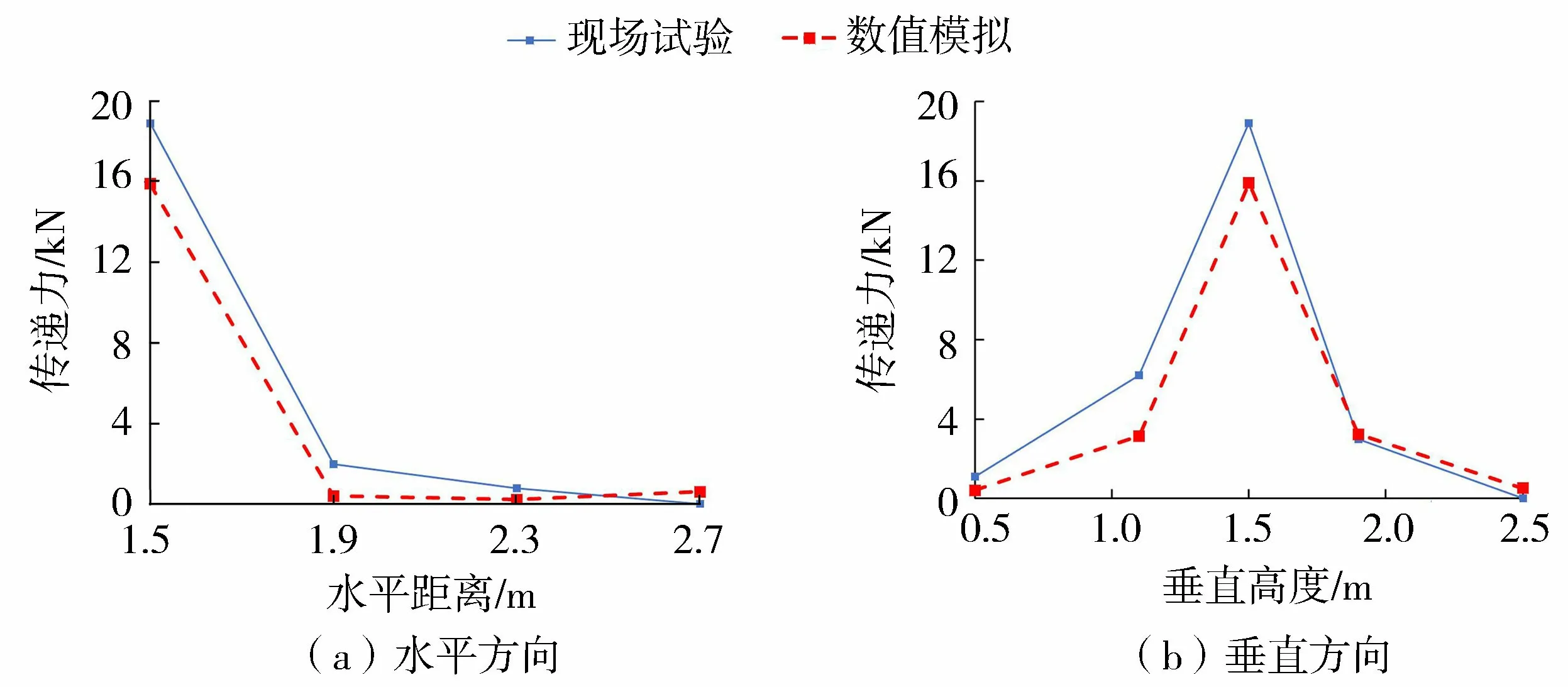
图6 空心砖缓冲层传递力分布Fig.6 Distribution of transfer force of hollow brick buffer layer

3 数值模拟结果与分析

统一使用标定得到的数值模型参数，分别建立孔隙率为28%、42%、54%以及保持孔隙率不变孔隙数目为2、8、18、32、50的空心砖有限元模型(图7)进行不同孔隙率和孔隙数目的数值模拟试验。28%孔隙率的2孔空心砖孔隙边长为10.6 cm，孔隙深度为19 cm，8孔、18孔、32孔和50孔的空心砖是由2孔空心砖孔隙按边长2等分、3等分、4等分、5等分得到，孔隙边长分别为5.30 cm、3.53 cm、2.65 cm和2.15 cm，孔隙深度均为19 cm。孔隙数目表现的是空心砖的孔隙分布状况，孔隙数目越少其孔隙分布越集中，反之则表示孔隙分布越均匀。由不同空心砖有限元模型进一步探讨孔隙率和孔隙分布对空心砖缓冲性能的影响。

图7 不同孔隙数目的空心砖Fig.7 Hollow bricks with different number of holes

3.1 孔隙率对缓冲性能的影响

图8为不同孔隙率的2孔空心砖缓冲层在混凝土球撞击时的滚石冲击力-位移关系，其中位移表示为混凝土球在空心砖缓冲层上的侵彻深度。随着孔隙率的增大，混凝土球的冲击力在不断减小，其侵彻深度在不断增加。42%孔隙率的空心砖缓冲层比28%孔隙率的空心砖缓冲层减小了 13%的滚石冲击力，增大了9%的侵彻深度，54%孔隙率的空心砖缓冲层比28%孔隙率的空心砖缓冲层减小了23%的滚石冲击力，增加了14%的侵彻深度。可见，增大空心砖的孔隙率，可以有效减小滚石冲击力，使得空心砖缓冲层获得更好的缓冲性能，这是由于空心砖孔隙率的增大可以使得空心砖的变形空间增大，从而降低空心砖的抗压强度，增大空心砖缓冲层的侵彻深度，使其缓冲性能也变得更好。图8结果与Gibson-Ashby模型[20-22]预测的多孔材料抗压强度与孔隙率关系的结果一致，两种模型中材料屈服强度都与孔隙率呈正相关关系。由此可以得出，以空心砖作为缓冲垫层材料时应当适当增大其孔隙率以增强其缓冲性能。

图8 不同孔隙率的滚石冲击力-位移曲线Fig.8 Rolling rock impact force-displacement curve under different porosity

由图9可知，不同孔隙率的空心砖缓冲层在传递力上有着较大差异，孔隙率越大其传递力越小。以2孔空心砖为例，28%孔隙率的空心砖缓冲层最大传递力为109 kN，当孔隙率增加到42%时，最大传递力减小到93 kN，降低了15%；当孔隙率增加到54%时，最大传递力减小到59 kN，降低了46%。可见增大空心砖孔隙率能够有效地减小滚石的冲击力和垫层的传递力，提高空心砖缓冲层的缓冲性能。

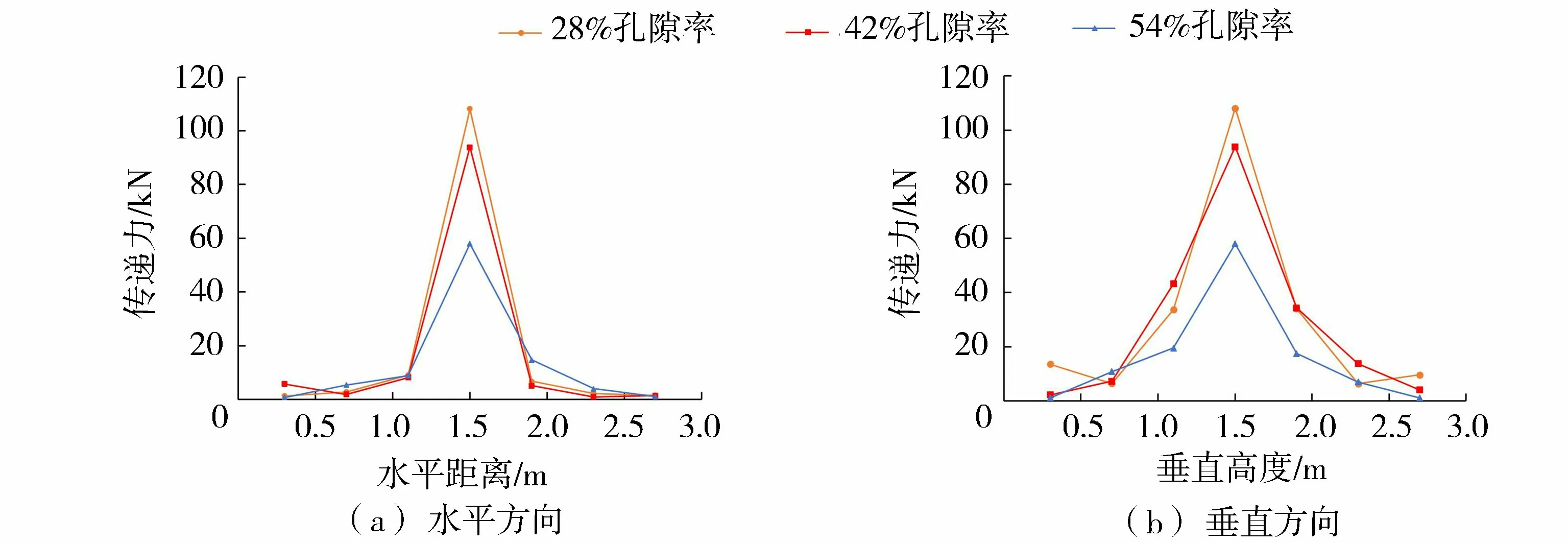
图9 不同孔隙率空心砖缓冲层传递力分布Fig.9 Distribution of transfer force of hollow brick buffer layer with different porosity

此外，对比水平轴上的传递力与垂直轴上的传递力，对于2孔空心砖可以发现，垂直轴上的传递力传递距离为0.80 m，水平轴上的传递力传递距离为0.45 m，垂直轴上的传递力扩散角明显大于水平轴上的传递力扩散角，这是由于滚石冲击力只能沿着孔隙壁传递，而空心砖在摆放时孔隙是在垂直方向的，所以孔隙壁也沿着垂直方向，这就导致了滚石冲击力更容易在垂直方向而不是水平方向上传递，从而垂直方向上力传递得更远。因此，以空心砖作为垫层材料时可以通过错开空心砖孔隙方向来增大其传递力扩散角，从而起到更好的缓冲作用。

3.2 孔隙分布对缓冲性能的影响

由图10可以看出，在28%孔隙率下，滚石的侵彻深度都随着孔隙数目的增大而增大，其中8孔、18孔、32孔、50孔的空心砖分别比2孔空心砖产生的侵彻深度增加了12%、 41%、120%和132%。可见，随着孔隙数目的增多，孔隙分布越趋于均匀，空心砖结构本身更容易发生破坏和压缩变形，能在更大的位移上吸收滚石的冲击能量。

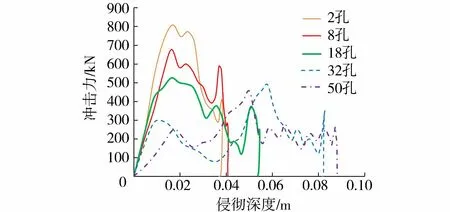
图10 不同孔隙数目的滚石冲击力-位移曲线(28%孔隙率)Fig.10 Rolling rock impact force-displacement curve with different number of pores distribution (28% porosity)

另一方面，如图11所示，在28%、42%、54%孔隙率下，8孔空心砖缓冲层比2孔空心砖缓冲层分别减小了16%、13%和10%的滚石冲击力峰值，18孔空心砖缓冲层比2孔空心砖缓冲层分别减小了32%、26%和23%的滚石冲击力峰值，32孔空心砖缓冲层比2孔空心砖缓冲层分别减小了39%、39%和36%的滚石冲击力峰值，50孔空心砖缓冲层比2孔空心砖缓冲层分别减小了44%、46%和45%的滚石冲击力峰值。可见，相同的孔隙率，孔隙分布越均匀，即孔隙数目越多，减小的滚石冲击力就越大，这是由于孔隙分布越均匀，空心砖越趋向于泡沫结构，其吸能效果越好。

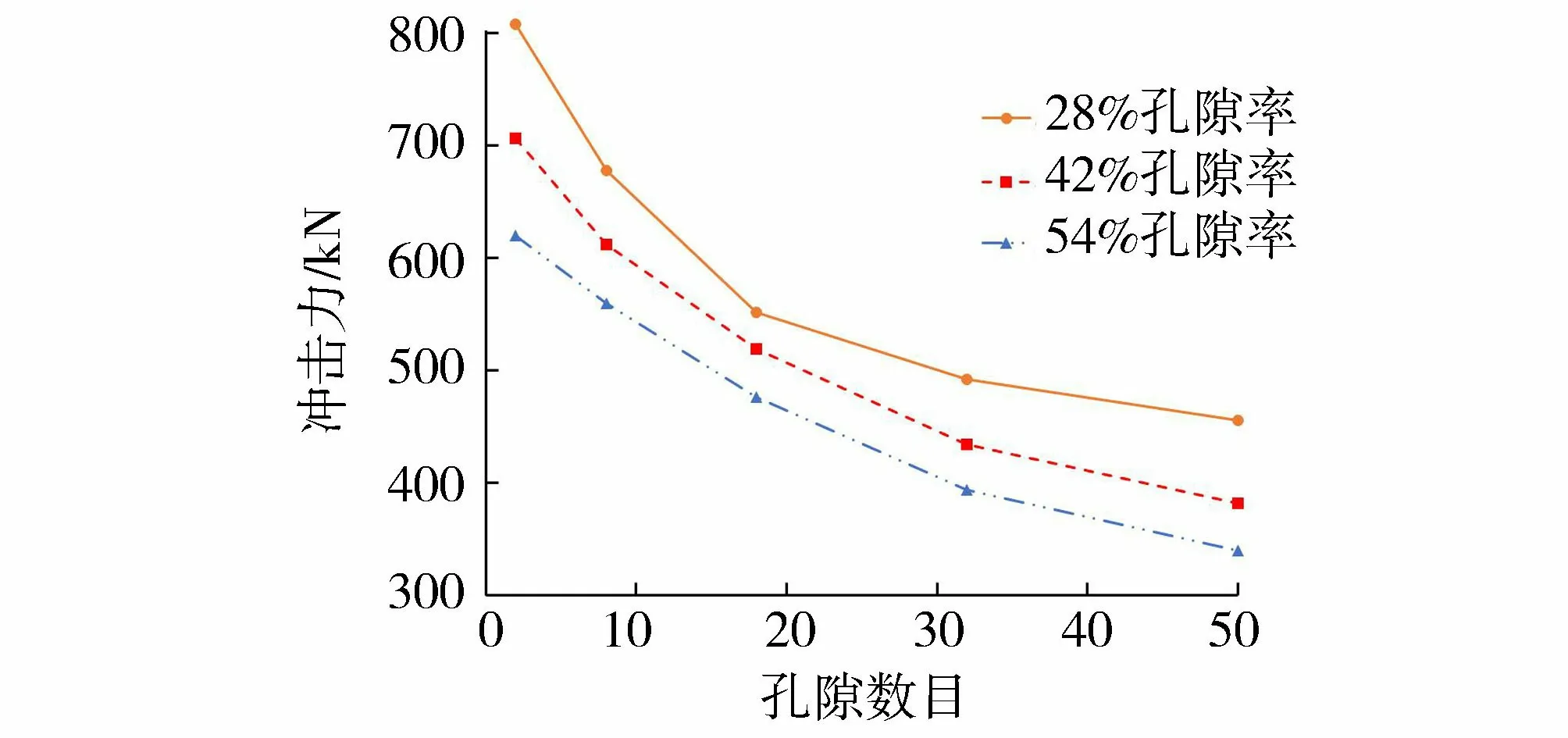
图11 滚石冲击力峰值随孔隙数目的变化Fig.11 Variation of peak impact force of rolling rock with the number of pores

图12为28%孔隙率时空心砖缓冲层传递力随空心砖孔隙数目的变化。其中，2孔、18孔、50孔空心砖缓冲层最大传递力分别为109 kN、94 kN和74 kN。空心砖孔隙数目从2孔增加都18孔再增加到50孔，最大传递力分别减小了23%和32%。因此，增加空心砖孔隙数目能够有效减小最大传递力。同时可以看出，与2孔空心砖缓冲层相比，当孔隙数目增加到50时，垫层传递力的横向传递距离由0.45 m增加到了0.75 m，传递距离增加了67%，垫层传递力扩散角由48°增加到70°，增大了46%，这是由于当增加孔隙数目时，空心砖的横向内支撑变得更加密集，逐渐承担起横向传递力的作用，使得滚石冲击力能沿着空心砖横向和纵向均匀传递。因此，以空心砖作为垫层材料时可以通过增加空心砖孔隙数目来增大其传递力扩散角，减小垫层最大传递力，从而起到更好的缓冲作用。

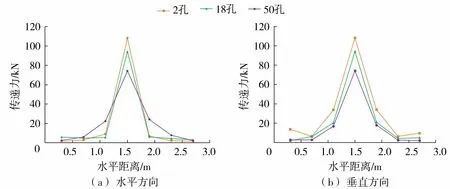
图12 不同孔隙数目空心砖缓冲层传递力分布(28%孔隙率)Fig.12 Transfer force distribution of hollow brick buffer layer with different number of pores(28% porosity)

3.3 滚石冲击位置对缓冲性能的影响

当更改滚石冲击的撞击点位置，即撞击点由中心偏移到距中心点30 cm的位置时，不同孔隙分布的空心砖表现出了不同的缓冲性能(图13)，即滚石冲击2孔、8孔空心砖时滚石冲击力出现较大的离散性，冲击18孔、32孔、50孔的空心砖时滚石冲击力离散性较小。由图14可以看出，随孔隙数目增加，滚石冲击力的标准差先急剧减小，孔隙数目增加到32后标准差趋于平缓。原因在于对于大孔隙空心砖，当滚石冲击在空心砖的内支撑、空腔、两砖黏结处时，空心砖缓冲性能表现出较大的差异，而小孔隙空心砖由于均匀的孔隙分布使得滚石冲击力能够在其上均匀地传递，从而具有较为均一的缓冲性能。因此，当采用孔隙率相同的空心砖作为缓冲垫层材料时，应采用小孔隙结构的空心砖，因为其对滚石冲击位置不敏感，滚石冲击力离散性较小，具有较为均一的缓冲性能。

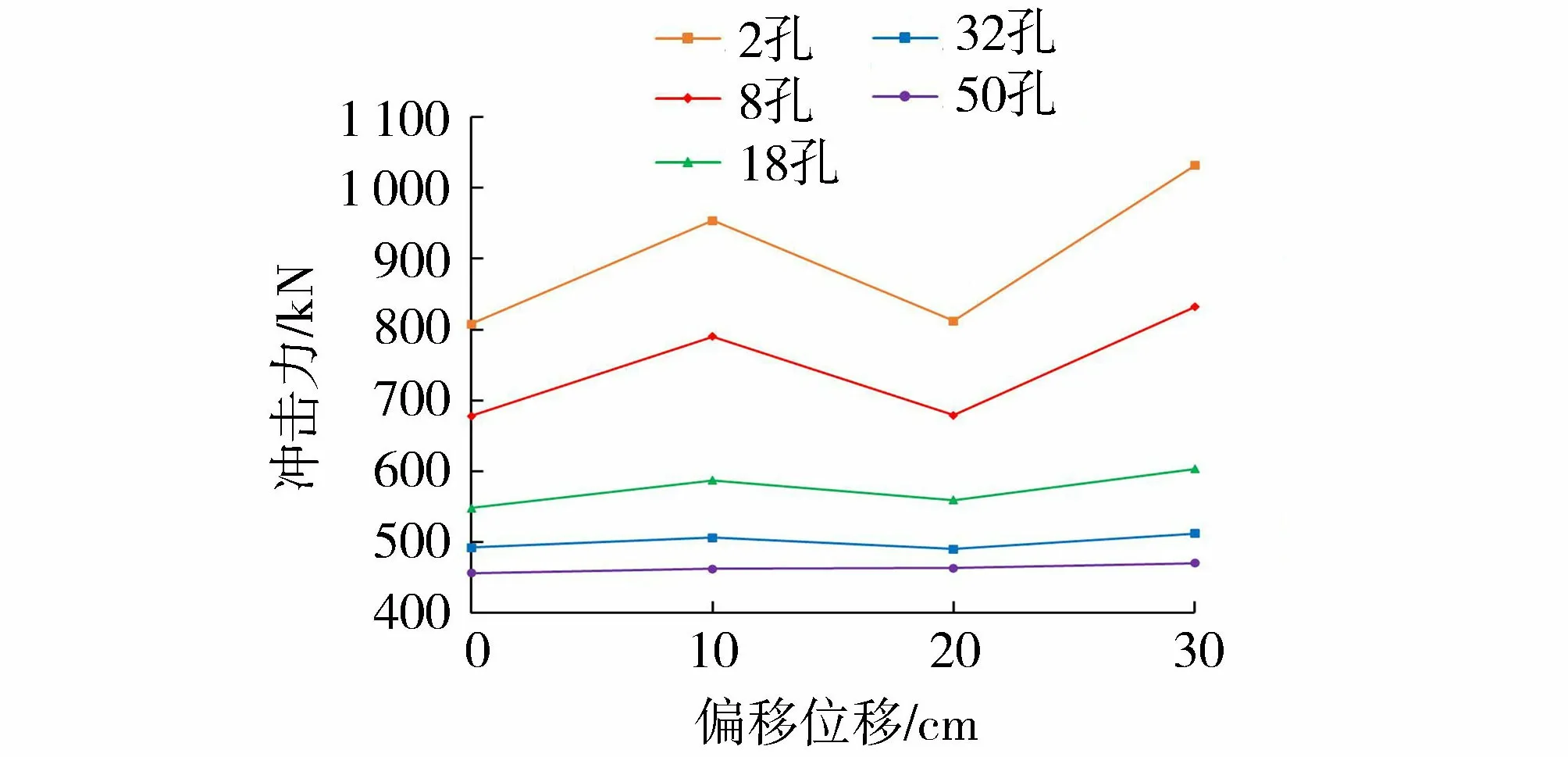
图13 滚石冲击力峰值随冲击位置变化(28%孔隙率)Fig.13 Variation of maximum boulder impact force with various impact point location(28% porosity)

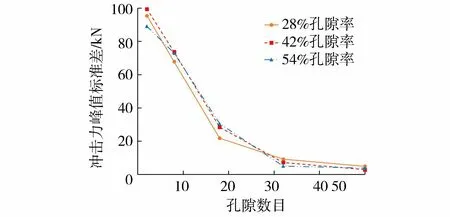
图14 滚石冲击力峰值标准差随孔隙数目的变化Fig.14 Variation of standard deviation of peak impact force with the number of pores

4 结 论

a.空心砖(2孔)孔隙率由28%增加到54%，其侵彻深度增加了14%，滚石冲击力峰值减小了23%。空心砖孔隙率的增大可以增大空心砖的变形空间，降低空心砖的抗压强度，提高空心砖的缓冲性能。

b.28%孔隙率的空心砖孔隙数由2孔增加到50孔，最大侵彻深度增加了132%，滚石冲击力峰值减小了44%。相同的孔隙率，孔隙分布越均匀，即孔隙数目越多，减小的滚石冲击力就越大，其吸能效果越好，更小的孔隙更容易破碎从而耗散能量。

c.滚石侵彻深度随着孔隙数目的增大而增大，孔隙分布越均匀，空心砖结构本身更容易发生破坏和压缩变形，能在更大的位移上吸收滚石的冲击能量。孔隙分布越均匀，滚石冲击力随冲击点位置改变的离散性越大，空心砖缓冲层表现出更为均一的削减冲击力性能。

d.空心砖孔隙数目由2孔增加到50孔，垫层传递力横向传递距离增加了67%，传递力扩散角增大了46%。 滚石冲击力主要沿空心砖孔隙壁传递，错开空心砖孔隙方向以及增加孔隙数目来增大其传递力扩散角，能起到更好的缓冲作用。