高减速比准双曲面齿轮设计与切齿试验
魏冰阳,仝昂鑫,张 辉,邓效忠
(河南科技大学机电工程学院,河南洛阳 471003)
高减速比准双曲面齿轮设计与切齿试验
魏冰阳,仝昂鑫,张 辉,邓效忠
(河南科技大学机电工程学院,河南洛阳 471003)
高减速比准双曲面齿轮的设计重点在节锥的确定和轮齿几何系数的选取。本文给出了少齿轮数准双曲面齿轮设计的几何限制条件,节锥设计新的收敛条件。以小轮体积最大为目标,通过优化求解的方法,确定了大、小轮的节锥。运用Matlab和UG软件对齿数比为3∶60的准双曲面齿轮进行了三维仿真,最后在GH-35机床上完成了切齿试验,验证了少齿数高减速比准双曲面齿轮在理论和实践上的可行性。
准双曲面齿轮;节锥;少齿数;仿真
0 引言
机器人、机电一体化集成技术的发展对齿轮传动装置的功率密度提出了很高的要求,为少齿数大减速比准双曲面齿轮提供了广阔的发展空间。准双曲面齿轮重合度大、运转平稳、承载能力强、空间配置灵活,尤其在高减速比传动时仍能保持较高的传动效率,同等条件下,其传动效率比普通蜗杆传动高15%以上[1],且制造工艺优良,大小轮均可采用硬齿面磨削工艺制造,故能保持长期的啮合精度。目前,国外一些精密分度、数控机床伺服、机电一体化设备中开始采用少齿数大减速比准双曲面齿轮替代蜗轮或行星齿轮传动[1]。文献[2]利用节锥变位的方法,通过三维仿真分析了大速比准双曲面齿轮传动的可行性。文献[3-4]在分析小轮齿形异变和啮合限制条件的基础上,完成了齿数比为4∶41的准双曲面齿轮的三维仿真和切齿。本文在上述研究的基础上,提出了准双曲面齿轮节锥设计新的收敛条件,利用综合变位、优化设计的方法,给出了齿数比为3∶60的准双曲面齿轮的几何参数,完成了三维仿真和切齿试验。
1 节锥设计
1.1 几何限制条件
对于准双曲面齿轮,美国齿轮精度标准(AGMA)对齿数有一定限制,小轮的齿数不得小于5,小轮与大轮的齿数和不应小于40。当小轮齿数减小到5个以下时,必须考虑的因素有:啮合限制条件、切削条件、强度平衡条件。
1.1.1 二类啮合界限点限制条件
准双曲面齿轮存在二类啮合界限点,为避免齿面出现二类啮合界限点,可通过限制极限压力角的办法来解决[5]。限制极限压力角计算公式为:
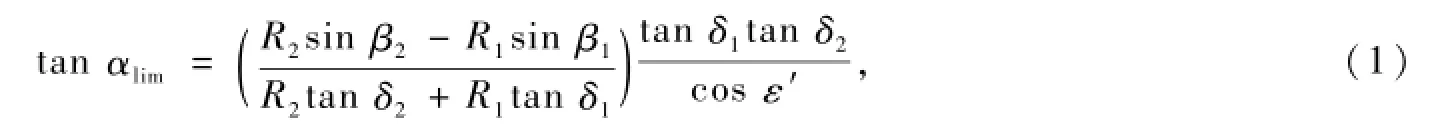
式中,符号的意义见文献[6],下同。本例限制极限压力角α<8°。
1.1.2 极限曲率半径
在准双曲面齿轮设计上,为了保证轮齿两侧相同的啮合特性,要求极限曲率半径rlim为:

极限曲率半径等于刀盘半径rc作为节锥设计的收敛条件。为了提高工作侧的啮合强度,现在新的设计理念有意采用非对称设计。因此,高减速比的准双曲面齿轮不再把此作为必须的收敛条件,而仅把其作为一个设计约束,即

1.1.3 切削限制条件
当齿数比达到一定数值后,大轮的节锥角将接近90°,切削时大轮面锥将会与刀盘发生干涉,因此,应限制大轮的节锥角:

因小轮的齿数很少,为避免其根切,同时防止其强度与大轮差别太大,根据传动比的大小限制其当量齿数:

本例限制小轮当量齿数不少于50齿。
1.1.4 几何限制条件
小轮的偏置距应在合适的范围内,要求:

为了避免轴向力过大,限制大轮的螺旋角:

对于给定的传动比,准双曲面齿轮的节锥并不唯一。要唯一的确定一对节锥,经典的设计方法给出了诸多的限制条件,这在没有计算机的年代当然是有意义的。对于高减速比设计,对极限曲率半径与刀盘半径之间的关系不再作严格的限制。
1.2 新设计的收敛条件
为保证小轮的强度,以准双曲面齿轮的小轮加大因数取最大值为目标求解。加大因数的计算公式如下[6]:
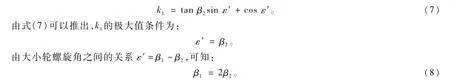
式(8)说明当大轮或小轮的某一螺旋角为定值时,按照该条件准双曲面齿轮的小轮的体积可达到最大。
根据式(1)~式(8),可确定大小轮的节锥参数为:大小轮螺旋角、大小轮节锥角、节锥顶点到交叉点的距离。
2 轮齿几何设计
轮齿的几何设计主要根据大轮中点的参数确定大、小轮的齿顶高、工作齿高、齿根角、根锥、面锥等参数[6]。这一部分主要在于选取合适的齿高系数和齿顶高系数,避免齿顶变尖,同时通过综合变位有意增大小轮的外径。
2.1 小轮齿顶厚的限制
小轮的齿顶宽受径向和切向变位系数的影响。本文设计的少齿数准双曲面齿轮的大轮采用成形法加工,故可以通过大轮精切的刀顶距来调整小轮的齿顶宽。大轮的刀顶距W2的计算公式为:

中点法向弧齿厚:
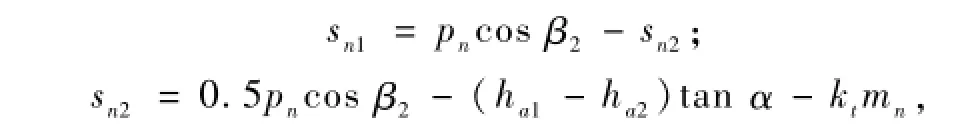
式中:α为中点平均压力角;pn为中点齿距,pn=πmn;kt为齿厚系数;ha1、ha2分别为小轮和大轮的齿根高;mn为小轮中点模数。
小轮的齿顶宽为:
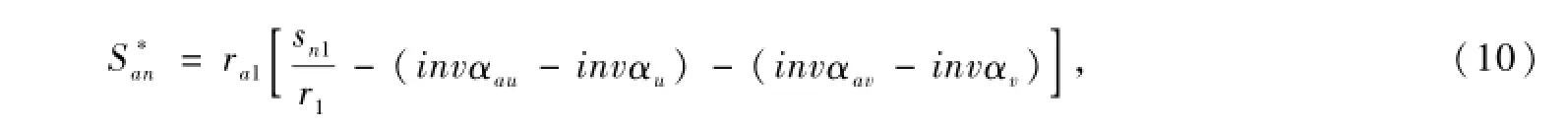
式中:ra1为小轮齿顶圆半径;r1为小轮分度圆半径;αau、αav分别为小轮左侧和右侧齿顶压力角;αu、αv分别为小轮左侧和右侧节点处压力角。
式(10)的值一般不应小于0.4倍的中点法向模数,即0.4mn。
2.2 最小齿槽宽的限制
要确保齿轮加工时良好的切削条件,小轮内端的最小齿底槽宽应做出一定的限制,不能太小,否则会给刀具的制造及切齿造成困难。该值一般也限定为0.4mn。其计算公式为:

式中:jmin为法向侧隙;pin为内端处的法向周节,
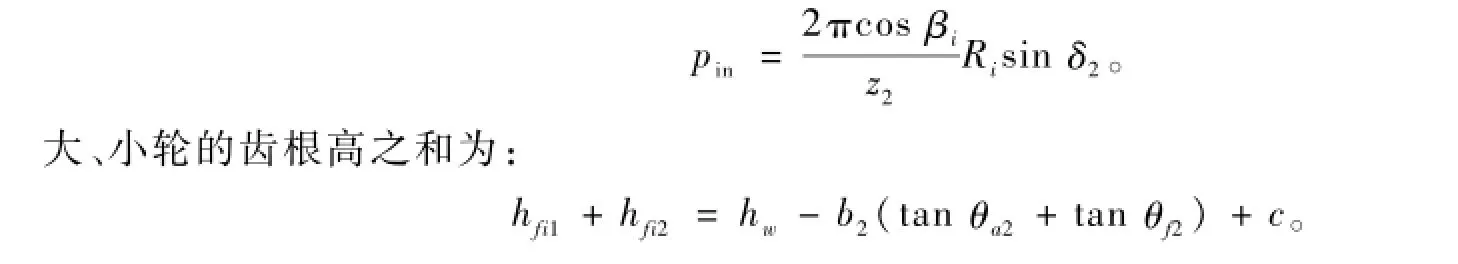
3 几何参数的计算
3.1 选择基本参数
一般情况下,需给定的基本参数为:大小轮齿数(z2,z1)、大轮节圆半径(r2)、轴夹角(∑)、偏置距(E2)、刀盘半径(rc)。
这些基本参数可根据用途、结构、经验或优化方法确定[6]。
3.2 节锥设计
以式(1)~式(7)为约束,以式(8)为目标,优化求解大小轮的节锥参数:小轮节锥参数δ1、β1、tz1,大轮节锥参数δ2、β2、tz2。
3.3 轮齿几何参数计算
根据式(10)和式(11)的限定条件,选取合适的齿高系数、齿顶高系数和弧齿厚修正系数。计算轮齿的几何参数:大小轮齿顶高、工作齿高、齿根角、根锥、面锥等参数[6]。根据上述过程,利用MatLab编程计算得到3∶60准双曲面齿轮的几何参数,如表1所示。

表1 齿轮的几何参数
4 轮齿的三维仿真与切齿试验
4.1 轮齿的三维仿真
大轮节锥角大于75°时都采用成形法加工,而本例的大轮节锥角达到了85°,所以其更接近于冠轮的形状,其理论齿廓也更接近于直线廓形。利用Matlab软件编程计算出三维离散坐标点[5],然后导入到UG软件中进行三维实体造型[7],得到成形法60个齿的大轮形状,如图1所示。然后,利用大轮包络小轮的原理,仿真小轮的实体模型,小轮的实际加工模型与全共轭模型齿面会有几到几十微米修形量的差别,不影响对轮齿形状的判断。小轮的三维模型如图2所示。在大轮和小轮的实体建模过程中,没有考虑轮齿的啮合侧隙,这不影响对轮齿几何拓扑结构、齿顶变尖、根切的判断[8]。由图2可看出:小轮齿数减小到3个齿后,齿形没有发生异变,说明所选取的螺旋角、变位系数合适[9]。当减速比达到20时,3齿小轮的方案是可行的。

图1 成形法60齿大轮

图2 准双曲面3齿的小轮
4.2 切齿试验
为了进一步检验齿数比为3∶60准双曲面齿轮的设计,在GH-35铣齿机上进行了切齿试验。大轮利用成形加工,大轮面锥与刀盘没有干涉现象发生[10]。在大轮切齿过程中发现85°几乎是大轮面锥的极限值,否则刀盘将与其干涉,破坏齿的切削。

图3 3∶60齿的准双曲面齿轮
由于所选齿轮模数小,小轮利用普通滚切法双面加工。切制出的大、小轮如图3所示,其轮齿形状与前述所建立的三维实体模型(见图1和图2)外形上一致[11],验证了本文关于少齿轮大速比准双曲面齿轮设计方法的可行性。
由于所选算例齿轮尺寸小,而本次试验重点在研究高减速比准双曲面齿轮的齿形变化,所以没有进行滚检试验。下一步研究工作的重点将在控制其接触质量上。
5 结论
(1)高减速比准双曲面齿轮设计的关键在节锥的确定和轮齿几何系数的选取,恰当的节锥参数、轮齿参数可避免轮坯干涉和小轮的齿形异变。
(2)对于接触质量要求不是很高的小模数高减速比准双曲面齿轮可以利用双面法加工。
(3)对于传动比到达20的准双曲面齿轮,在几何设计和加工上仍然是可行的。
[1]Hermann S.Tribology Aspects in Angular Transmission Systems Part VIII:Super-Reduction Hypoid Gears[J].Gear Technology,2011(8):42-48.
[2] 张金良,方宗德,邓效忠.大速比准双曲面齿轮的设计与分析[J].机床与液压,2007,35(4):13-15.
[3] 魏冰阳,张辉,仝昂鑫,等.少齿数大速比准双曲面齿轮的三维仿真与试验[J].机械传动,2014,38(10):155-157.
[4] 张辉.少齿数大减速比准双曲面齿轮的三维仿真与实验[D].洛阳:河南科技大学,2014.
[5] Litvin F L.Gear Geometry and Applied Theory[M].New Jersey:Prentice Hall,1994.
[6] 邓效忠,魏冰阳.锥齿轮设计的新方法[M].北京:科学出版社,2012:54-55.
[7] 王利环,魏冰阳.准双曲面齿轮节锥参数设计的新方法[J].河南科技大学学报:自然科学版,2008,29(2):25-27.
[8] 杨建军,魏冰阳,周彦伟,等.准双曲面齿轮设计加工集成系统的开发[J].河南科技大学学报:自然科学版,2004,25(25):17-20.
[9] 陈武营.准双曲面齿轮三维接触椭圆的可视化[J].机械传动,2008,32(2):27-29.
[10] 刘芳,吴训成,张钦超.准双曲面齿轮副几何参数设计研究现状与展望[J].上海工程技术大学学报,2010,24(2):127-129.
[11] 王红芳.基于Excel、Matlab与UG的准双曲面齿轮精确建模研究[J].现代机械,2010(5):11-12,49.
TH132
A
1672-6871(2015)05-0015-04
国家自然科学基金项目(51375144)
魏冰阳(1966-),男,河南嵩县人,教授,博士,博士生导师,主要从事齿轮啮合理论及先进制造技术方面的研究.
2015-01-23

