基于Vista的地震资料叠后偏移处理方法研究

李锦锋，崔 寓，郭志强，张 波，马永钊

(1.西安石油大学 地球科学与工程学院，陕西 西安 710065; 2.延长石油下寺湾采油厂 勘探开发研究所，陕西 延安 716000;3.西安森舍电子科技有限责任公司，陕西 西安 710100; 4.甘肃省地矿局第二地质矿产勘查院，甘肃 兰州 730020;5.中国石油集团测井有限公司，陕西 西安 710200)

基于Vista的地震资料叠后偏移处理方法研究

李锦锋1，2，崔 寓3，郭志强3，张 波4，马永钊5

(1.西安石油大学 地球科学与工程学院，陕西 西安 710065; 2.延长石油下寺湾采油厂 勘探开发研究所，陕西 延安 716000;3.西安森舍电子科技有限责任公司，陕西 西安 710100; 4.甘肃省地矿局第二地质矿产勘查院，甘肃 兰州 730020;5.中国石油集团测井有限公司，陕西 西安 710200)

叠后偏移处理能使倾斜反射层归位到它们真正的地下界面位置，并使绕射波收敛，横向分辨率提高。在分析了有限差分法和克希霍夫积分法偏移原理的基础上，借助Vista软件对地质模型资料进行叠后偏移处理与分析，通过改变叠后偏移处理过程中的参数后可以得到不同的偏移剖面，然后结合地质模型对这些不同的偏移剖面进行对比、分析和研究，取得了很好的效果。结果表明叠后偏移在一定范围内仍有其优势。

叠后偏移成像;有限差分法;克希霍夫积分法;Vista地震数据处理系统

地震资料经过水平叠加以后，输出成果是时间剖面。时间剖面上每个样点的记录，代表了地面共接收点的自激自收记录。当地层界面是水平时，其反射点就在该自激自收点的正下方。当然实际地层界面总是存在一定的倾角且由于地下地质构造的复杂性，如普遍存在的断层、地裂缝、地下暗穴及地层尖灭等现象，叠后地震波场变得十分复杂，直接造成成像结果不真实，横向分辨率降低［1－3］。这时时间剖面上的记录点与真实反射点的水平位置就产生了偏移，由于偏移现象的存在，使得地震解释工作很不方便。而偏移处理则能使倾斜反射界面归位、绕射波收敛，从而提高横向分辨率，使地震剖面能够再现地下构造的真实形态［2］。

近年来有关借助Vista软件进行实际地震资料叠后偏移处理与分析的外文文献很多，但有关这方面的国内文献相对较少。本文结合前人研究成果［4－9］，在分析了有限差分法和克希霍夫积分法偏移原理的基础上，借助Vista软件对地质模型资料进行叠后偏移处理与分析。结果表明对地质条件相对简单且信噪比较低的地震记录来说，采用叠后偏移处理的效果优于叠前偏移处理，因此叠后偏移在一定范围内仍有其优势。

1 叠后偏移成像方法原理

1.1 有限差分法波动方程偏移原理

在实际地震数据成像处理中有限差分法波动方程偏移是经常使用的一种偏移方法。为了方便求解上行波波动方程，需要将上行波波动方程转换为时间－空间域的表达式，然后将其表示为某种近似形式，最后在时间－空间域研究其差分方程及其求解问题［2，3］。

1.1.1 上行波的时间－空间域方程

为了减少计算工作量，保持计算的相对稳定性，利用浮动坐标系进一步将上行波波动方程简化，然后再利用傅里叶变换的微积分性质可以得到浮动坐标系下时间—空间域上行波各级近似方程［2］。

经简化后的浮动坐标系下45°上行波方程(一级近似式)

经简化后的浮动坐标系下45°上行波方程(二级近似式)

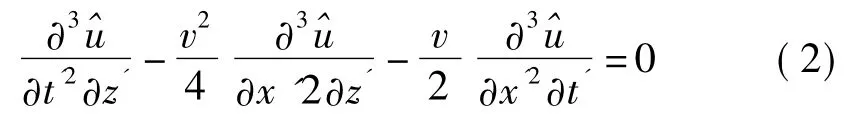
2.1.2 有限差分法波动方程偏移的实现

以浮动坐标系下15°上行波方程(1)为例，讨论有限差分偏移的具体解法［2］。经化简后(1)式可以重新写成

在习惯上，偏移结果在时间域τ显示，而不在深度域显示

在(x，τ，t)坐标系下，方程(3)可改写为

在下面的定解条件下求解该微分方程:

(1)侧线两端外侧的波场为零;

(2)地震记录最大时间之外的波场为零;

(3)地震观测的地震记录是给定的边界条件;

(4)当t=τ时的波场函数所组成的剖面就是偏移后的输出剖面。

为了在定解条件下求得该微分方程的数值解，将差分方程近似微分方程。由于在该微分方程式中包含二阶偏导项和二阶混合偏导项，因此采用12点差分格式，可得

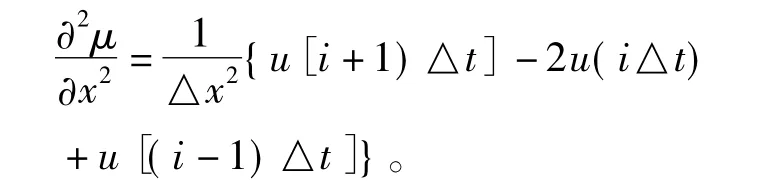
定义向量I、T为

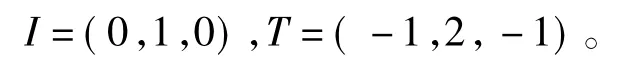
令向量

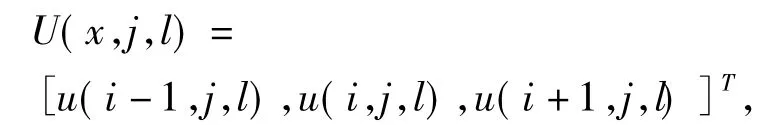
将以上各式带入(1－5)式中经简化后可得该微分方程的隐式差分表达式:

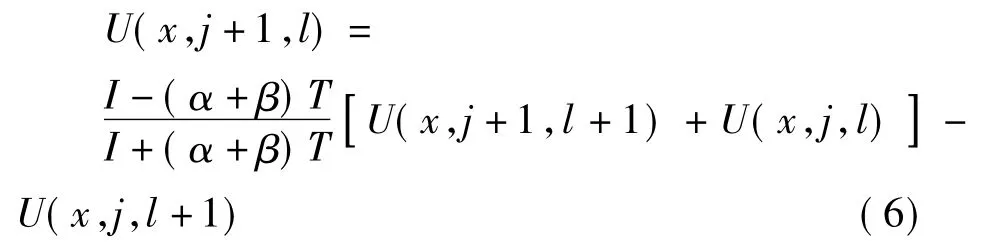
然后利用追赶法可求该解差分方程［2］。

在波场延拓的过程中，对于某一个τ值，从tmax开始向t减小的方向进行，一直计算到t=τ为止。t=τ时刻的波场就是该深度上的成像波场值。然后τ增加一个步长△τ，依此类推，就可以得到各深度上的成像波场值［2，3］。

1.2 克希霍夫积分法偏移原理

地震数据成像处理中经常使用的另一种叠后偏移处理方法就是克希霍夫积分法偏移［2］。

纵波齐次波动方程积分解为

式中 Q—扰动区内的闭合曲面;

n—Q的外法线;

r—p(xp，yp，zp)至Q上个点的距离;

u(xp，yp，zp，t)—Q内某点p(xp，yp，zp)于t时刻的波场值。

2 地震资料叠后偏移处理与分析

下面通过对地质模型数据的处理结果来说明用有限差分偏移和克希霍夫偏移对叠后地震资料进行偏移处理的效果。

2.1 地质模型

实际地质模型如图1所示。模型基本参数:单边放炮，每炮48道接收，共151炮，炮间距2 m，最小偏移距为4 m，采样率为500 ms。该地质模型中包括三条正断层，地裂缝和地下暗穴等地质特征。

图1 实际地质模型

2.2 有限差分法叠后偏移处理与分析

借助Vista软件对该模型数据进行处理后得到的未偏移的共中心点(CMP)叠加剖面如图2所示。由于未做偏移处理，从叠加剖面中可明显看出有绕射波的存在，断面反射波向下倾方向偏移，反射波同相轴发生错断等现象。

图3、图4和图5分别为借助Vista软件进行叠后偏移处理后得到的15°有限差分偏移剖面、45°有限差分偏移剖面和65°有限差分偏移剖面。从三个偏移剖面的对比中可以看出，15°有限差分偏移剖面和45°有限差分偏移剖面对倾角较大的反射波归位效果不好。剖面的畸变减小了，但断面波未完全归位，只有部分偏移后的地震波能够正确地收敛到产生他们的位置上去，而且振幅也只能够部分相对地保真，它们均受一定倾角的制约;65°有限差分偏移剖面中，偏移后的断面波真正归位，绕射波能够正确地收敛到产生他们的位置上去，而且振幅也能够很好地保真，三条正断层、裂缝及地下暗穴等均能构清晰地观测到，基本上真实地反映了模型剖面的形态。

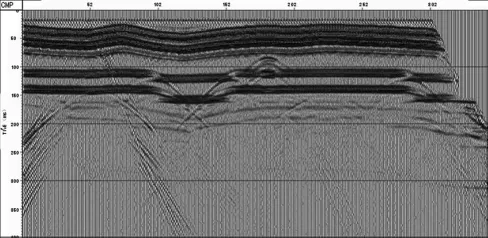
图2 共中心点(GMP)叠加剖面

图3 15°有限差分偏移剖面

图4 45°有限差分偏移剖面

图5 65°有限差分偏移剖面

通过对15°有限差分偏移剖面、45°有限差分偏移剖面和65°有限差分偏移剖面的对比分析中我们能够发现，较高的倾角近似方程得到了较好的偏移结果，随着近似方程级数的提高，偏移剖面越来越接近理想偏移效果。

2.3 克希霍夫积分法进行叠后偏移处理与分析

借助Vista软件运用克希霍夫积分法进行叠后偏移处理后得到的偏移剖面如图6所示，从该剖面中可以看出，偏移后的断面波真正归位，绕射波能够正确地收敛到产生他们的位置上去，而且振幅也能够很好地保真。裂缝能够比较清晰的观测出来，三条正断层也能构清晰地显示出来，暗穴也能构较好地观测到。从偏移剖面图中可以看出偏移剖面的信噪比高，断层清楚，波形特征相对来说得到了很好的保持。真实地反映了模型剖面的形态。

图6 克希霍夫偏移剖面

2.4 两种叠后偏移方法比较

通过对15°有限差分偏移剖面、45°有限差分偏移剖面和65°有限差分偏移剖面的仔细观察中能够发现，较高的倾角近似方程得到了较好的偏移结果，随着近似方程级数的提高，偏移剖面越来越接近理想偏移结果。但其受反射界面倾角的限制，当倾角较大时，产生频散现象，使波形畸变。克希霍夫偏移方法能适用于任意倾角的反射界面，对剖分网格要求较灵活［7，9］。通过对有限差分偏移剖面和克希霍夫偏移剖面的对比中我们能够发现，当对横向速度处理要求不是很严格且偏移噪声相对较小的情况下克希霍夫积分法叠后偏移要优于有限差分法叠后偏移。

3 结论

(1)有限差分波动方程叠后偏移中，近似波动方程的级数越高，其偏移剖面越来越接近理想偏移结果，65°有限差分偏移剖面(三级近似波动方程)的效果最佳。当地质条件相对简单且偏移噪声相对较小的情况下克希霍夫积分法叠后偏移的效果要优于有限差分法叠后偏移的效果。

(2)对低信噪比的地震记录来说，如果地质条件不是十分复杂，借助Vista软件对地震资料进行叠后偏移处理与分析，其偏移效果常常优于叠前偏移，因此叠后偏移在一定范围内仍有其优势。

［1］陆基孟，王永刚.地震勘探原理［M］.北京:中国石油大学出版社，2009.

［2］牟永光，陈小宏，刘洋，等.地震数据处理方法［M］.北京:石油工业出版社，2009.

［3］马在田.地震成像技术—有限差分法偏移［M］.北京:石油工业出版社，1989.

［4］Yilmaz O，Claerbout JF.Pre－stack partialmigration［J］. GEOPHYSICS，1980，(12):1753－1779.

［5］刘喜武，刘洪.波动方程地震偏移成像方法的现状与进展［J］.地球物理学进展，2002，04:582－591.

［6］Samuel H Gray.Seismic migration problems and solutions［J］.Goephysics，2001，(66):1622－1640.

［7］张关泉.利用低阶偏微分方程组的大倾角差分偏移［J］.地球物理学报，1986，03:273－282.

［8］Ristow D，Ruhl T.3－D implicit finite－differencemigration bymulti－way splitting［J］.Geophysics，1997，62(2):554－567.

［9］马在田.高阶近似有限差分偏移［J］.石油地球物理勘探，1982，17:6－15.

［责任编辑 李晓霞］

Study on Post－stacked M igration M ethod of Seism ic Data w ith Vista System

LI Jin－feng1，2，CUIYU3，GUO Zhi－qiang3ZHANG BO4，MA Yong－zhao5

(1.School of Earth sctences and Engtheering，Xian ShiYou University，Xi'an 710065，China; 2.Exploration and Production Research Institute of Yanchang Oilfield Yan'an Shaanxi716000; 3.Xi'an senshe Electronic Technology Corporation Xi'an shaanxi710100; 4.No.2 Geology and Mineral Exploration Team，Gansu Province Bureau of Geology and Mineral Exploration and Development，Lanzhou Gansu 730020;5.China Petroleum logging Xi'an shaanxi710200)

The process of post－stackmigration canmake the sloping reflectors homing to the true sub－surface position，the diffracted wave converge，and the lateral resolution improve.With the results of previous studies，in this paper，the principle of finite differencemethod and Kirchhoff integration method is introduced firstly，and with the help of Vista system，the geologicalmodel data is analyzed by the post－stack migration.Differentmigration profile is a good result

by the different values of post－stack migration parameters.Afterwards，combined with the geologicalmodel，the relatively good comparison，analysis and research is successfully carried out for the different migration profile.The results show that the post－stack migration still has its advantageswithin a certain range.

post－stackmigration;finite differencemethod;Kirchhoff integralmethod;Vista seismic data processing system

TE122.1

A

1004－602X(2015)03－0062－04

10.13876/J.cnki.ydnse.2015.03.062

2015 -04 -25

李锦锋(1987—)，男，陕西榆林人，延长石油助理工程师，西安石油大学在读硕士研究生。