一种基于局部对比度的分块压缩感知多聚焦图像融合算法*
黄晓生,付思思,曹义亲
(华东交通大学软件学院,江西南昌330013)
近年来,随着压缩感知 (CS)理论的发展[1],基于CS的图像融合方法研究受到了越来越广泛的关注,出现了不少基于CS的图像融合算法。这些算法总的来说包含三个部分:源图像的压缩测量、测量值的融合以及融合结果的图像重构。其中源图像的压缩测量主要涉及稀疏基、测量矩阵及采样率的选择,测量值的融合主要涉及如何针对不同特点图像设计有效的融合策略,融合结果的重构主要涉及在保证适当重构图像质量及重构效率的基础上如何选择或设计重构方法等。文献[2]提出了一种基于傅立叶稀疏、双星采样模式、绝对测量值最大融合策略的最小全变分 (min-TV)重构的压缩感知域图像融合方法。文献 [3]提出了一种基于傅立叶稀疏域、星形采样模式、min-TV重构的压缩感知域图像融合方法,其融合策略是将CS测量值进行小波变换,再分别对对逼近系数及细节系数进行融合。文献[4]提出了一种基于小波稀疏域、双放射状采样、min-TV重构的融合方法。文献[5]提出了一种基于傅立叶稀疏域、双星采样模式、简单最大融合规则的基于Bayesian重构的图像融合算法。文献 [6]提出了一种基于非下采样轮廓波变换 (NSCT)和压缩感知的图像融合方法,该方法对NSCT低频部分采用传统的加权融合,而对NSCT域高频部分则进行星形CS采样、标准差(SD)加权融合、min-TV重构的压缩感知融合,最后高频部分与低频部分一起经逆变换得到融合图像。文献 [7]与 [6]相似,该方法对图像小波变换 (DWT)的低频部分采用传统的平均加权融合,对高频系数进行部分哈达玛矩阵测量、简单绝对值取大融合、正交匹配追踪 (OMP)重构的压缩感知融合,最后低频与高频部分一起经逆变换得到最终融合图像。这些方法从CS采样模式、融合规则及重构方法等方面对CS图像融合进行了研究,取得了良好的融合效果,但是这些算法都是基于整幅图像进行全局压缩采样,所需存储空间大、重构复杂度高。对此,文献 [8]受 JPEG及MPEG中DCT分块编码思想的启发,提出了分块压缩感知 (BCS)方法。该方法更适于实时应用环境,其测量算子可以很容易地存储和实现,同时,由于对每个图像块的处理都是独立进行,因此可以更容易地获得初始解,从而大大加快重构过程[8],文献 [9]提出了一种基于BCS的数字水印方法。在图像融合领域,文献 [10]采用SBHE(Scrambled Block Hadamard Ensemble)对图像进行分块压缩测量、测量值采用熵加权平均融合规则、重构方法则采用梯度投影稀疏重构 (GPSR)。文献 [11]则先进行SBHE分块压缩测量,然后根据分块CS测量值进行相似性分类,对低相似度块、中相似度块以及高相似度块分别采用不同的融合规则,最后通过GPSR重构融合图像。文献[12]提出了一种基于块稀疏贝叶斯学习 (BSBL)的压缩图像融合算法,该算法首先将待融合图像进行离散小波变换,采用随机观测矩阵获取CS观测向量;然后对CS观测向量进行小波分解,对小波分解近似系数和细节系数进行加权融合,得到融合压缩观测向量;最后通过 BSBL方法重构融合图像。文献[13]则首先利用随机结构矩阵 (SRM)对输入图像进行分块压缩采样,再对压缩测量采用线性加权策略融合,最后采用迭代阈值投影重构算法重构融合图像。这些方法通过对图像进行分块压缩采样,减少了存储空间要求和降低了重构计算复杂度,但这些方法并不是针对多聚焦图像融合进行设计,没有考虑多聚焦图像的特性,不能对聚焦及非聚焦区域进行准确定位,从而影响了其对多聚焦图像融合的性能。
对此,本文针对聚焦图像的特点,提出一种基于局部对比度的BCS的多聚焦图像融合方法。该方法首先对2D图像进行分块压缩采样,然后基于CS域局部对比度的方法选择清晰图像块进行初步融合,再通过多数滤波进行一致性验证得到最终的CS融合结果,最后采用SPL(Smoothed Projected Landweber)算法进行重构[14],在有效消除分块效应的基础上,实现融合图像的高质量重构。
1 基于BCS的多聚焦图像融合
传统的多聚焦图像融合方法,通常通过选择聚焦清晰的区域进行融合[15],因此,如何有效地区分聚焦区域与离焦区域就成了有效进行多聚焦图像融合的关键。目前,主要有空域、频域和基于统计的几类清晰度评价方法[16],但在CS域,如何评价图像的清晰度,相关研究还很少。本文在文献[17]的基础上提出一种基于CS域的局部对比度的CS域清晰度度量,并应用于多聚焦图像融合中。算法的总体思想是,根据BCS原理,首先将源图像分成大小为B×B的非重叠块并对每一块进行矢量化,再选择合适的测量矩阵以一定的采样率对矢量化信号进行压缩测量,通过比较各块的清晰度来判断聚焦与离焦块,将不同源图像中最清晰的部分融合在一起,然后通过一致性校验对融合块进行校正得到最终融合结果,最后采用SPL算法对融合结果进行图像重构。基于BCS的多聚焦图像融合框架如图1所示。
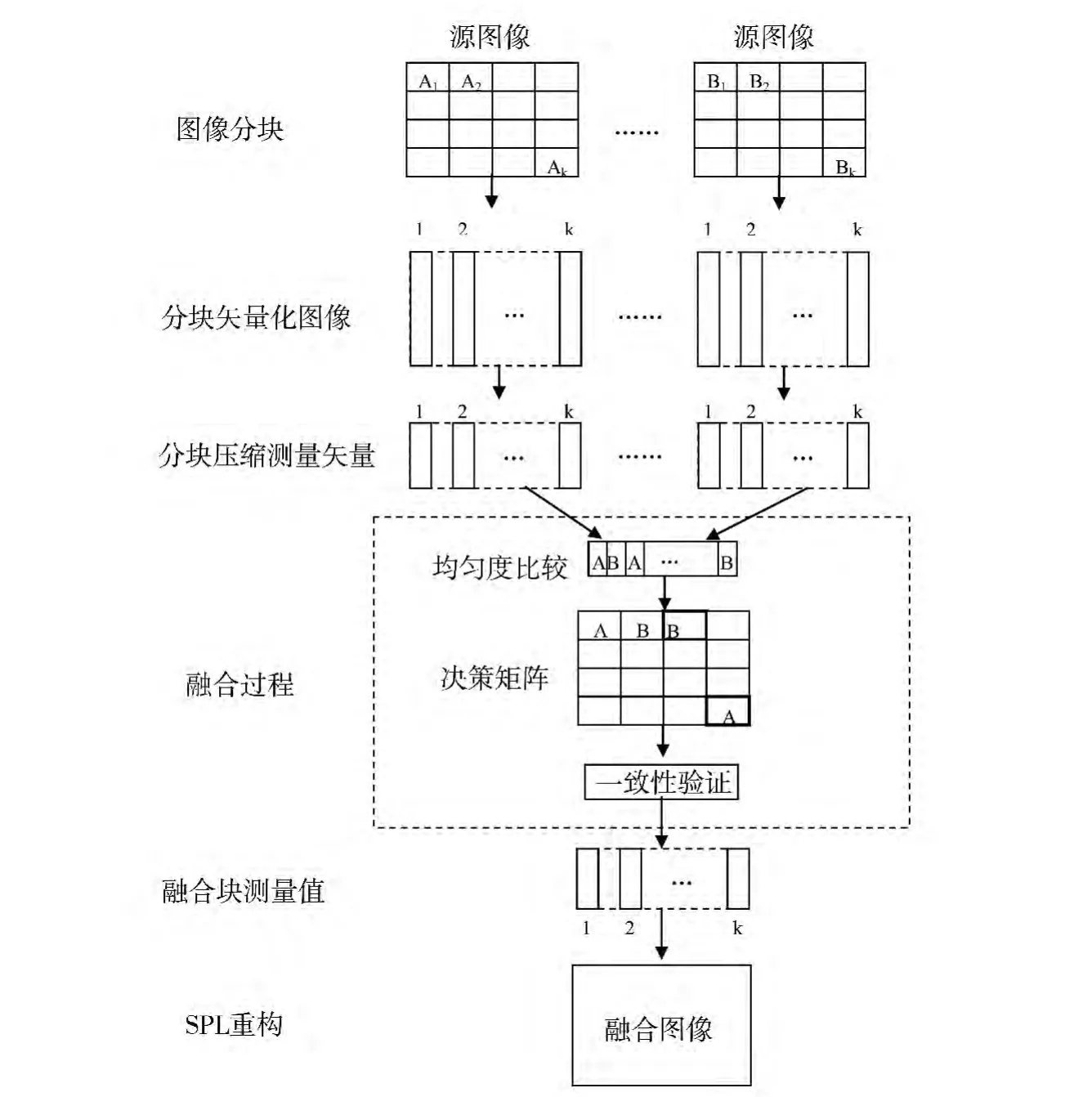
图1 基于BCS的多聚焦图像融合框架Fig.1 Multi-focus image fusion framework based on BCS
1.1 分块大小与采样率
根据BCS理论,一幅Ir×Ic大小的图像,划分为一个个B×B大小的小块,对其中每一块用相同的测量矩阵ΦB进行CS测量,设xi为第i块图像经矢量化后的信号,则相应的CS测量向量yi可表示为



由于BCS中只需要存储一个nB×B2的测量矩阵,而不是全局测量的n×N测量矩阵,因此,BCS具有更高的存储效率[8]。
在上述BCS中,块大小B与采样率S=n/N是影响BCS性能的重要参数,对重构图像的质量及重构速度都将产生重要影响。一般来说,B越小,则用于存储测量矩阵所需的内在较小,重构速度较快,B越大,则重构质量较好,但算法复杂度较高。采样率越大,重构图像质量越好,但计算量较高,而采样率小则重构质量较低,但计算量较小。如设分块大小为B,采样率为S,则对每一块进行CS测量的测量矩阵大小为S*B2×B2,向量化后为S*B4×1向量,可见,测量矩阵所需的内存与采样率及块大小的4次方成正比。因此,需要根据实际应用要求,选择合适的分块大小及采样率,本文根据文献 [8,13]建议采用B=32,采样率为0.3。
1.2 测量矩阵
在上述BCS中,除块尺寸及采样率外,一个结构良好的测量矩阵对于有效的压缩采样与精确重构同样非常重要。对于2D图像,随着尺寸增加,数据量迅速增加,因此,应选择运算速度快、存储效率高、重构精度高和通用性强的测量矩阵。目前常用的高斯矩阵或伯努利矩阵,虽然通用性强,且只需要较少量的压缩观测就能实现信号的精确重构。但它们是完全非结构化的矩阵,其存储空间需求大和计算复杂度很高。而局部Fourier矩阵,虽计算速度快,且能简化采样系统硬件实现的复杂性,但局部Fourier矩阵只与时间域稀疏信号不相关、通用性差、存储空间需求大。此外,一些具有较低计算复杂度和近似最优重构性能的二值稀疏矩阵也可选为测量矩阵,但它们往往只与特定稀疏表示矩阵不相关,缺乏通用性。对此,文献 [18]提出了一种结构化随机矩阵 (SRM),其定义为

式中,R∈RB2×B2为均匀预随机化算子,它将信号转换为近似白噪声分布的不相关序列;F∈RB2×B2为具有快速计算速度的变换算法,如离散余弦变换(DCT)算子或快速傅立叶算子 (FFT),其目的是将预随机化信号的信息分散到所有测量点上;D∈Rnb×B2为下采样算子,其作用是从B2个DCT系数中随机抽取nb个元素作为压缩采样结果。通常,将nb与B2的比值定义为压缩采样率S。文献 [18]指出该矩阵几乎与所有正交矩阵 (除了单位矩阵)和多种稀疏信号都不相关,通用性强;同时,SRM作为测量矩阵时重建信号所需的测量数量几乎是最优的;另外,SRM还能分解成为许多结构化子矩阵或块对角化子矩阵的乘积,便于分块处理和线性滤波,具有低复杂度和快速计算特性。因此,本文采用SRM作为测量矩阵。
1.3 基于局部对比度的BCS融合
为区别多聚焦图像中清晰目标与模糊目标,文献[17]根据对比度敏感门限与背景亮度的非线性关系,提出了一种有效的衡量图像块均匀度的测度:对于图像f(x,y)中大小为n×n的块Bk,其定义为

其中μk为Bk的均值,ω(μk)为加权因子。该均匀度参数模拟人眼的视觉特性,突出了图像的对比度信息,以达到良好的视觉效果。根据上述定义的均匀度参数,可以比较准确地判定多聚焦图像中的清晰目标和模糊目标。
在CS框架下,图像经CS测量后,CS测量值之间失去了像素之间的结构关系,但根据CS理论[1],对于任意 K稀疏信号x,y,其2K阶约束等距 (RIP)条件可表示为

式中Φ为观测矩阵,‖·‖2表示向量的L2范数。式 (5)意味着在满足2K阶约束等距 (RIP)条件下,稀疏信号之间的距离与其测量值之间的距离很接近。因此,对两稀疏信号之间的比较可以由稀疏信号的测量值之间的比较来代替。据此,本文将图像块的CS测量值代替图像像素值,提出了一种CS域图像块对比度的清晰度度量,其定义如下:
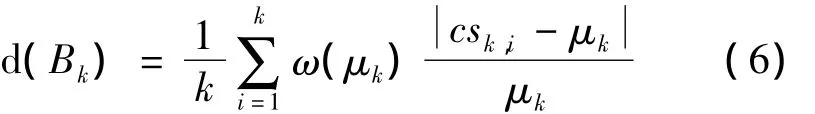
式中,μk为第k块的CS测量均值,csk,i为第k块CS测量分量,ω(μk)为加权因子,其计算公式为

根据式 (6)计算出源图像各分块的局部对比度后,图像按如下规则进行融合:

即选择清晰度高的图像块进行融合。其中,Fcsk为融合CS图像的第k块,A_csk为A图像中的第k块,B_csk为B图像中的第k块。
1.4 一致性验证
在实际图像中,如果一个场景中的某个区域处于源图像A的聚焦区,则根据上面的计算过程,这些块应该全部选自A,但有时可能出现误差导致错误地选择源图像 B中的图像块,对此,文献[19]提出用多数滤波 (majority filter)的思想进行一致性验证。本文参照其思想进行一致性验证,具体做法是根据图像分块情况,构造一大小为(Ir/B)×(Ic/B)的决策矩阵,每个图像块对应决策矩阵中相应位置的一个元素 (如图1所示),其初始值为根据式 (8)选择的图像块来源,若为A代表相应图像块来自A,否则为B。多数滤波过程为:若根据式 (8),某一融合图像块来自源图像B,而包围它的周围图像块则来自A,则将这个图像块重变为选自A,最终得到修正后的决策矩阵,最后据此决策矩阵获得的融合CS结果,并由SPL算法重构出融合图像。重构的基本过程是对每一次迭代,首先通过自适应维纳滤波来消除块效应及平滑图像,然后将滤波后的信号向凸集投影,再通过阈值操作过滤噪声,最后再将过滤后的信号再投影回该凸集,进行下一次迭代。
2 仿真实验与结果分析
本文实验环境为Pentium Dual Core CPU 3.06 GHz,2 GB 内存,Windows XP SP3,Matlab 2009b,实验采用了二组具有不同聚焦图像进行实验,其中一组为左右聚焦图像,另一组为上下聚焦图像,如图2所示,其中(a)为左聚焦时钟图像,(b)为右聚焦图像,(c)为上聚焦图像,(d)为下聚焦图像。实验结果从主观和客观两个方面进行比较,主观评价通过目视或目测对融合图像质量进行评价,客观评价主要通过客观评价指标进行比较。本文分别采用信息熵 (IE)、互信息 (MI)和平均梯度 (AVG)作为客观评价指标,对算法效果进行了评价。其中信息熵主为反映图像包含的平均信息量的多少,熵值越大,说明图像包含的信息量越大。互信息是评价融合图像与源图像之间的互信息,互信息越大,说明融合图像与源图像之间越相似,融合的图像质量越好。平均梯度是测量一个图像的对比度,平均梯度越大,图像的对比度越大。实验中块大小取B=32,采样率S=0.3,测量矩阵为结构随机矩阵。
首先,为验证一致性校验的效果,分别对两组图像进行一致性校验与不进行一致校验融合实验。结果如图3所示,从图中可以看出,二组实验图像经一致性校验后,主观视觉质量有明显改善,客观评价指标信息熵、互信息以及平均梯度各项客观指标也得到了改进,但算法运行时间有所增加。


图3 一致性校验效果比较Fig.3 Comparison between consistency verification and no consistency verification
为检验本文方法的性能,本文选择文献[11]、文献 [13]的方法作为参照,它们均为基于BCS的图像融合方法,但并不是针对多聚焦图像融合设计。同时,文献 [2]虽然是基于全局采样模式,但它采用的是最经典的绝对最大融合规则,因此,本文也选择其进行比较。实验中,文献[11]采用SBHE测量矩阵,文献 [13]采用SRM测量矩阵,采样率均为0.3。实验结果如图4、图5所示,其中图4为左右聚焦图像融合实验结果,图5为上下聚焦图像融合实验结果,从中可以看出,对于二组实验图像,无论是从主观视觉效果上看,还是客观上看,本文方法均取得了较好效果,文献[2]方法采用简单的绝对值取大融合规则,计算比较简单,但由于采用全局采样,需要占用大量内存,从而导致计算时间更长,同时主客观效果也较差。文献 [11]采用分类的方法,在一定程度上也区分了聚焦与离焦区域,因此获得了较文献[13]更好的主客观性能,但由于要进行分类,使算法运行时间较文献 [13]略长。

图4 左右聚焦图像不同融合方法效果比较Fig.4 Comparison of different fusion methods in left-right focus image fusion

图5 上下聚焦图像不同融合方法效果比较Fig.5 Comparison of different fusion methods in up-down focus image fusion
4 结论
本文针对多聚焦图像特点,提出了一种基于局部对比度的分块压缩感知的图像融合方法。该方法首先对融合源图像进行分块压缩采样,然后基于CS域局部对比度来选择清晰区域进行融合,再对选择的分块通过多数滤波方法进行一致性验证得到最终融合结果,最后由SPL算法在有效消除分块效应的基础上,实现融合图像的高质量重构。实验结果表示,与目前典型的基于BCS图像融合方法相比,本文方法结合了多聚焦图像特点,在运算速度及融合图像质量方面均具有较明显的改进。
[1]DONOHO D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2]TAO W,CANAGARAJAH N,ACHIM A.Compressive image fusion[C]// IEEE International Conference on Image Processing.New York,USA,2008:1308-1311.
[3]LI X,QIN S Y.Efficient fusion for infrared and visible images based on compressive sensing principle[J].IET Image Process,2011,5(2):141-147.
[4]黄晓生,戴秋芳,曹义亲.一种基于小波稀疏基的压缩感知域图像融合算法[J].计算机应用研究,2012,29(9):3581-3583.
[5]周红志,冯莹莹,王戴木.基于Bayesian压缩感知的融合算法[J].计算机应用研究,2013,30(2):613-615.
[6]邢雅琼,王晓丹,毕凯,等.基于非下采样轮廓波变换和压缩感知的图像融合方法[J].控制与决策,2014,29(4):587-591.
[7]孙永明,吴谨,刘劲,等.基于DWT的高频系数压缩感知图像融合[J].红外技术,2014,36(9):714-718.
[8]GAN L.Block Compressed Sensing of Natural Images[C]//Proceedings of the International Conference on Digital Signal Processing.Cardiff,UK,2007:403-406.
[9]赵慧民,蔡君,魏文国.一种分块压缩感知变采样率的指纹图像水印算法[J].中山大学学报:自然科学版,2014,53(5):14-19.
[10]LUO X Y,ZHANG J,YANG J Y,et al.Image fusion in compressed sensing[C]// IEEE International Conference on Image Processing,2009:2205-2208.
[11]LUO X Y,ZHANG J,YANG J Y,et al.Classiɦcationbased image-fusion framework for compressive imaging[J].Journal of Electronic Imaging,2010,19(3):1-14.
[12]刘哲,顾淑音,南炳炳,等.一种基于块稀疏贝叶斯学习的压缩图像融合算法[J].光子学报,2013,42(11):1365-1369.
[13]杨森林,万国宾,高静怀.基于分块压缩感知的遥感图像融合[J].计算机应用研究,2015,32(1):316-320.
[14]MUN S,FOWLER J E.Block compressed sensing of image using directional transforms[C]// Proceedings of the International Conference on Image Processing.Cairo,Egypt,2009:3021-3024.
[15]王宏,敬忠良,李建勋.一种基于分块的多聚焦图像融合方法[J].上海交通大学学报,2003,37(11):1743-1746.
[16]GARG R,GUPTA P,KAUR H.Survey on multi-focus image fusion algorithms[C]// Proceedings of 2014 RAECS UIET Panjab University Chandigarh,06- 08,March 2014:291-295.
[17]李树涛,王耀南,张昌凡.基于视觉特性的多聚焦图像融合[J].电子学报,2001,29(12):1699-1701.
[18]DO T T,GAN L,NGUYEN N H,et al.Fast and efficient compressive sensing using structurally random matrix[J].IEEE Transactions on Signal Processing,2012,60(1):139-154.
[19]LI H,MANJUNATH B,MITRA S.Multisensor lmage fusion using the wavelet transform[J].Graphical Models Image Processing,1995,57(3):235-245.

