广西旱灾对称性特征及趋势判断*
王文静,延军平,刘永林,曹永旺
(陕西师范大学旅游与环境学院,陕西西安710062)
IPCC第五次评估报告指出:1880-2012年,全球海陆表面平均温度呈线性上升趋势,升高了0.85℃,2003-2012年平均气温比1850-1900年平均气温上升了0.78℃[1],全球气候变暖加剧了旱涝等灾害的频繁发生。据统计,我国每年由于旱涝灾害造成的经济损失达2000亿元左右,约占国民经济总产值的3% ~6%[2]。国内外学者对旱涝等气象灾害展开了一系列的研究。CHOUBIN等[3]利用神经建模方法对半干旱流域的干旱进行预测;曾红伟等[4]运用TMPA降水数据对澜沧江流域的干旱进行评估;周振民等[5]建立BP神经网络模型,对郑州未来10 a的降水量进行预测;张遇春等[6]运用灰色系统的突变预测方法,建立各县区的突变预测模型,对黑河未来一定时期内干旱发生的时间进行预测;孙鹏等[7]基于马尔科夫模型对新疆的水文气象干旱进行了研究。但目前对于旱灾的预测方法繁琐且单一,且大多是分析历史数据来研究旱灾的发展规律,进而推断未来趋势。针对目前的灾害研究“单一手段多,综合方法少;害的风险多,灾的风险少;历史评价多,趋势判断少;学术研究多,减灾价值少”的现象,如果能把灾害简约出对称性结构,并由表及里去逼近灾害物理机理,逐渐提高重大自然灾害趋势判断水平,这可能是地理学对灾害研究的重要贡献[8]。因此,本文利用可公度法、蝴蝶结构图和可公度结构系对广西壮族自治区旱灾的对称性特征进行分析,从而丰富灾害趋势的研究案例,为地球科学认识对称性规律提供一种新思路,为准确的预测预报灾害提供一定的科学依据。
1 研究区概况
广西壮族自治区地处中国华南沿海,位于东经104°-112°,北纬20°-28°之间,北回归线横贯全区的中部,属于亚热带季风气候区,年降水量丰富,但由于受冬、夏季风的交替影响,降水量季节变化不均匀,旱涝灾害频繁发生。自古以来,广西受风、潮、洪、涝、旱的侵害,干旱灾害占60%,洪涝灾害占13%,其它灾害占27%[9]。旱灾的频繁出现给广西壮族自治区的经济、社会和人民生活造成了巨大的损失,制约了广西的发展。因此,研究广西壮族自治区旱灾的对称性特征并对变化趋势进行判断,对于今后的灾害预防具有极其重要的意义。
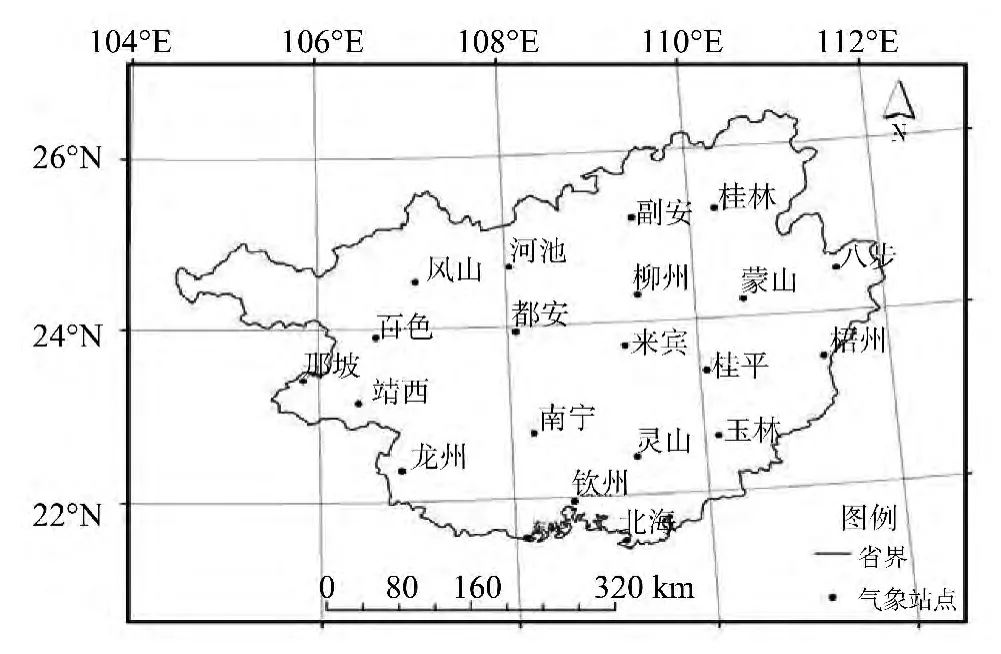
图1 研究区域示意图Fig.1 Location of study area
2 资料来源和研究方法
2.1 资料来源
1950-2000年广西壮族自治区灾情比较严重的干旱年份资料主要来源于《气象灾害大典 (广西卷)》[10],2000年以来的气象资料来自中国气象科学数据共享服务网,主要包括广西壮族自治区21个气象站点2000-2014年的逐月降水量数据。各个站点的旱灾等级是通过标准化降水指数(SPI)的公式根据逐月降水量计算而来,区域的旱涝等级是将各个站点的降水量求取平均值,然后转化成旱涝等级。
2.2 研究方法
2.2.1 标准化降水指数 (SPI) 由于降水量分布一般不是正态分布,而是一种偏态分布。所以在进行降水分析和干旱监测、评估中,采用Γ分布概率来描述降水量的变化。标准化降水指数就是在计算某时段内降水量的Γ分布概率后,再进行正态标准化处理,最终用标准化降水累积频率分布来划分干旱等级。其计算步骤为[11]:
假设某时段降水量为随机变量x,则其Γ分布的概率密度函数:

式中,β>0,γ>0分别为尺度和形状参数,β和γ可用极大似然估计方法求得,见式 (2):

确定概率密度函数中的参数后,对于某一年的降水量x0,可求出随机变量x小于x0事件的概率为:

利用数值积分可以计算用式 (1)代入式 (3)后的事件概率近似估计值。
降水量为0时的事件概率由式 (4)估计:

式中,m为降水量为0的样本数,n为总样本数。
对Γ分布概率进行正态标准化处理,即将式(3)、式 (4)求得的概率值代入标准化正态分布函数:

对式 (5)进行近似求解可得:

本研究对旱灾等级划分为5个等级 (表1)。

表1 标准化降水指数旱灾等级划分Table 1 Classification scales for SPI
2.2.2 可公度方法 可公度方法表示自然界事物之间的一种秩序,由天文学引入信息预测学[12-18]。可公度性是时间对称性的一种表现,它是周期性的一种扩展,可公度的特征就是不同长度的周期叠加后表现出的一种混合规律,它表达了系统元素中可以共同度量的某种规律[19]。传统的数理统计方法是求常态的方法,预测一段趋势,与之相反,可公度方法的信息预测理论是求变异的方法,确定突变的一个点。它的预测基础是灾害是过程,过去是存在,未来是秩序。
“有结构就有对称”,部分重大自然灾害可能更具有可公度性与时空对称性。可公度方法对于一些自然灾害的预测已经通过了历史的验证,取得了重要的成果。例如:1982年的华北大旱,1991年长江流域的洪水等都是其成功的典例。其方法为:
1)三元可公度计算公式。

其中a、b、c为自然灾害已经发生的年份,d为预测的自然灾害发生年份;
2)四元可公度计算公式。

其中预测下一次自然灾害发生年份Xi,Xi=Xj+ΔX,Xj为自然灾害最后一年发生年份。
3)五元可公度计算公式。
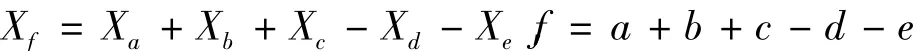
3 结果分析与讨论
依据统计资料和标准化降水指数的计算,统计出广西1950-2014年重旱的年份分别为:1955,1956,1962,1963,1966,1977,1980,1985,1986,1988- 1992,1999,2000,2004,2007,2009,2010,2011。相连的年份取起始年 (考虑到1988-1992年连旱时间太长且经过验证预测结果不变,故取起始年和结束年,简化计算量,提高效率)得到如下数列:
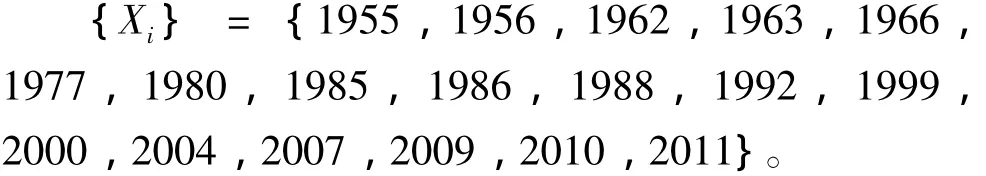
3.1 可公度趋势判断及验证
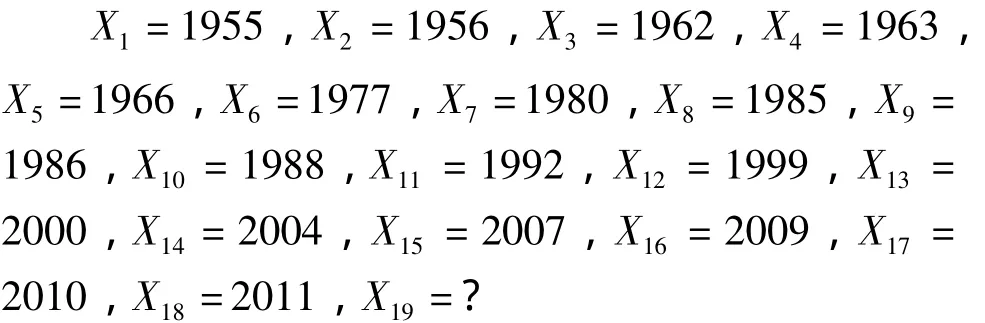
三元可公度计算结果为:2015年4组;2016年4组;2017年7组;2018年7组;2019年4组;2020年1组;2021年6组;2022年6组;2023年3组;2024年5组;2025年4组。其中,2017和2018年信号最强,其次是2021和2022年。
由此,我们可以推断广西未来旱灾可能发生年份的三元可公度式为:

对广西18次历史旱灾进行验证计算,得出的结果与实际的年份相一致,且每一个年份都能写出10组以上的可公度式,最多的达到了32组 (表2)。由此表明该地区的历史旱灾表现出良好的可公度性,可公度计算结果具有一定的说服力。

表2 三元可公度式验证表Table 2 The confirmation of drought based on commensurable method
四元可公度计算结果为:2015年56组;2016年35组;2017年29组;2018年28组;2019年27组;2020年18组;2021年15组;2022年18组;2023年10组;2024年7组;2025年2组。其中,2015年信号最强,其次是2016年和2017年。
五元可公度计算结果为:2015年116组;2016年106组;2017年97组;2018年79组;2019年69组;2020年52组;2021年56组;2022年42组;2023年39组;2024年31组;2025年19组。其中,2015年信号最强,其次是2016和2017年。
综上,由三元可公度频数计算结果可知2017和2018年旱灾信号最强;四元可公度计算结果知2015年信号较强;五元可公度分析同样得出2015年有较强的可公度信号。为了突显三元可公度的计算的结果,本文利用三元的原始计算结果与四元、五元频数计算结果的自然对数进行对比分析 (图2)。根据可公度趋势判断三元优先,同时参考四元、五元的原则,判断出广西下一次发生严重干旱的年份极有可能为2017年。
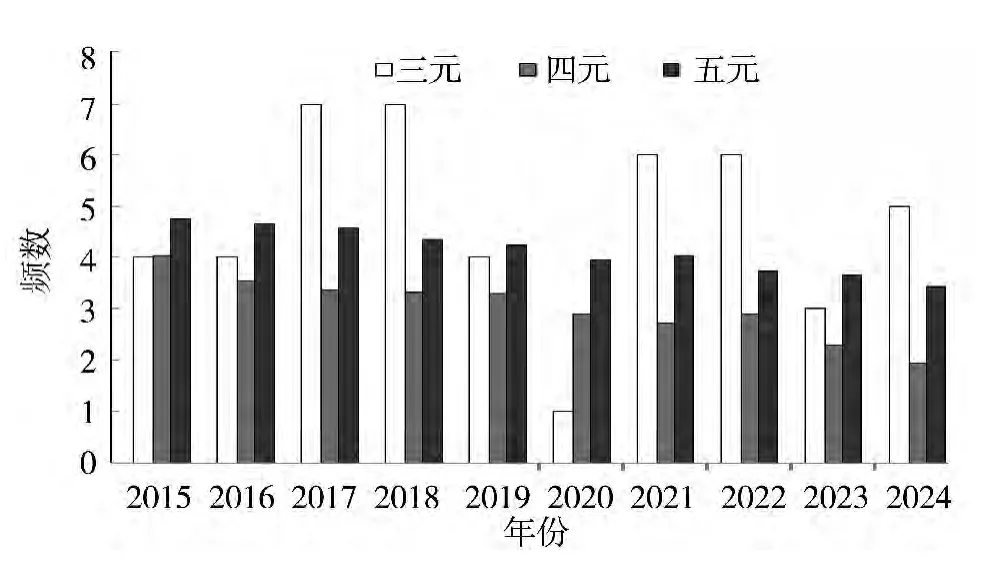
图2 广西重旱可公度计算频数Fig.2 The commensurability frequence of drought in Guangxi
3.2 蝴蝶结构图趋势判断
时间对称性是指某些地理现象的产生和变化存在一定的时间周期,且周期任意对应时刻都存在相同或相似的性状或状态[13]。蝴蝶结构图是自然灾害时间对称性结构的体现,是可公度方法关于时间结构认识的进一步表达[20]。蝴蝶结构图是建立在等时间间隔基础上,剖析时间对称性的一种方法,通过构建年份结构关系,绘制具有时间对称性特点的2组以上“蝴蝶结构图”来确认预测年份。根据可公度信息绘制蝴蝶结构图 (图3),进一步寻求广西重旱年的对称性结构。从图中可以看出,广西重旱总体上以1,6,7,8,11,22,25和30 a为主周期,其中与2017年相关的周期为6,7,8和25 a,与2017年相关的蝴蝶共4只,分别是2004-2010-2011-2017、2004-2010-2011-2017、1999-2007-2009-2017、1986-1992-2011-2017。近65 a来总共发生重旱事件为18次,实际参与判断2017年的事件有1955、1956、1963、1977、 1980、 1985、 1986、 1992、 1999、2000、2004年,共计11次。因此,2017年广西发生重旱的随机性概率为61.1%,不漏报的置信水平为57.9%。需要强调的是,没有参与实际预测的其他各周期,也可以表明此灾害时间具有其他可公度性时间规律,因此也具有实际的意义[19]。
3.3 可公度结构系趋势判断
可公度结构系是指从已经发生灾害的年份中筛选一种或几种与主周期相关的年份,然后根据时间间隔即周期关系构建一种类似于网状的结构,利用这种结构关系可进一步验证推演下一次灾害的发生年份[8]。因此,本文为了更加直观地描述研究区域的特征,基于时间对称性的周期特点,绘制了可公度结构系。由图4可知,可公度结构系的主体由矩形构成,纵向上以8和6a为主周期,横向上以3,7,10,12,22和48 a为主周期,横向周期和纵向周期相互套嵌,形成完整的网络结构,表现出了很好的时间对称性。由可公度结构系判断出该地区2017年发生重旱的信号较强,这与可公度和蝴蝶结构图的趋势判断结果相一致。

图3 广西重旱年蝴蝶结构图Fig.3 The butterfly structure of drought in Guangxi
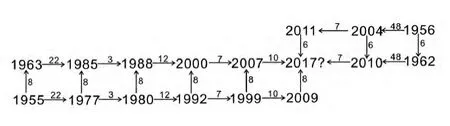
图4 广西重旱年可公度结构系图Fig.4 The commensurable structure of drought in Guangxi
3.4 相关机理分析
ENSO事件是太平洋赤道带大范围内海洋和大气相互作用后失去平衡而产生的一种气候现象。ENSO是年际气候变化的最强信号,许多重大气象灾害的发生与它密切相关,它对全球气候产生了重要的影响。从图5中可以看出,1950-2014年广西发生干旱事件18次,11次与ENSO事件发生年份一致,频率为61.1%,在厄尔尼诺年发生的频率为27.8%,在拉尼娜年发生的频率概率为33.3%,说明在拉尼娜年广西降水通常偏少而导致干旱的发生,这与柳林秀[21]、李秀存等[22]的研究结果相一致。

图5 广西重旱年份与ENSO事件关系图Fig.5 Relationship between drought in Guangxi and ENSO events
太阳黑子是太阳活动的基本标志,其相对数量变化可作为判断太阳活动强弱的标志[23]。太阳黑子数目多的年份称为太阳活动高峰年,用M表示,黑子数目少的年份称为太阳活动低峰年,用m表示。广西1950-2014年55 a间经历了从1943年开始的第18、19、20、21、22和23个太阳黑子周期,期间共出现5个M年,分别是1957、1970、1980、1989和2000年;出现5个 m年,分别是1964、1976、1986、1996和2008年[24]。从图6可以看出,干旱发生在黑子数M年附近的有2次,m年附近的有4次,发生在太阳黑子数上升和下降阶段的干旱次数比例为2∶1。因此,可以看出太阳黑子数上升的时期是干旱多发的时期,即太阳活动较强的年份即太阳黑子相对数较多的年份,干旱发生的概率较大。
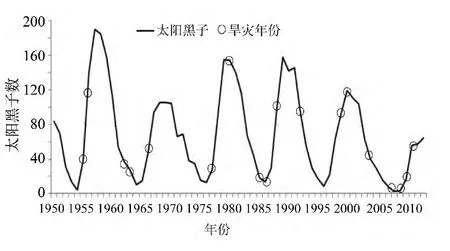
图6 广西重旱年份与太阳黑子的关系Fig.6 Relationship between the drought and the relative sunspot number in Guangxi
3.5 讨论
自然灾害的可公度性是从一些随机事件中提取并非偶然的信号,它是一种灾害趋势的研究方法,由于受到人类活动及其他因素的干扰使它的适应性具有一定的区域性[25]。再加上事物的不断发展变化,如何有效地对可公度理论预测的可能发生年份进行筛选,以排除虚假信号,是今后研究中要考虑的问题。
干旱预测是一个较复杂的问题,旱涝灾害的致灾因子和相关的物理机理是多样的。本文在可公度理论的基础上,对研究区的旱灾与ENSO事件以及太阳黑子等外部致灾因子进行了相关分析,而对灾害的对称性物理机理未能从理论上进行推演证明。因此,在今后的灾害趋势判断研究中,应综合考虑多种诱灾因子,运用多种统计学方法,进一步探讨旱涝灾害发生的相关物理机理。
4 结论
本文通过采用可公度法、蝴蝶结构图、可公度结构系对广西旱灾进行趋势判断及其对相关机理进行分析,得出以下结论:
1)经三元可公度验证,1950年以来广西的旱灾表现出良好的可公度结构特征,具有明显的时间对称性。
2)通过可公度方法的分析,结合蝴蝶结构图和可公度结构系,广西2017年发生旱灾的信号较强。
3)广西旱灾的发生年份与ENSO事件表现出较好的相关性。尤其是干旱发生年与拉尼娜年表现出更好的相关性。
4)太阳黑子对广西旱灾发生具有一定的影响。结合旱灾年份及太阳黑子数变化趋势的分析,发现旱年基本出现在太阳黑子的上升段,即太阳活动逐渐增强的阶段。
[1]秦大河,THOMAS S.IPCC第五次评估报告第一工作组报告的亮点结论[J].气候变化研究进展,2014,10(1):1-5.
[2]巢纪平,李崇银,陈英仪,等.ENSO循环机理和预测研究[M].北京:气象出版社,2003.
[3]CHOUBIN B,KHALIGHI-SIGAROODI S,MALEKIAN A,et al.Drought forecasting in a semi-arid watersged using climate signals:a neuro-fuzzy modeling approach[J].Journal of Mountain Science,2014(6):1593-1605.
[4]曾红伟,李丽娟,李九一.TMPA降水数据在澜沧江流域干旱监测中的评估(英文)[J].地理学报:英文版,2012,22(2):273-282.
[5]周振民,谢滨帆.BP神经网络在郑州市旱灾预测中的应用及防灾减灾对策[J].中国农村水利水电,2011(12):97-100.
[6]张遇春,张勃.黑河中游近49年降水序列变化规律及干旱预测——以张掖市为例[J].干旱区资源与环境,2008,22(1):84-88.
[7]孙鹏,张强,白云岗,等.基于马尔科夫模型的新疆水文气象干旱研究[J].地理研究,2014,33(9):1647-1657.
[8]延军平.重大自然灾害时空对称性研究[M].陕西:陕西师范大学出版总社有限公司,2013.
[9]张凌云,简茂球.AWTP指数在广西农业干旱分析中的应用[J].高原气象,2011,30(1):133-141.
[10]温克刚,杨年珠.中国气象灾害大典-广西卷[M].北京:气象出版社,2007.
[11]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.气候干旱等级(GB/T20481-2006)[S].北京:中国标准出版社,2006.
[12]翁文波.可公度性[J].地球物理学报,1981,24(2):151-154.
[13]李双双,延军平,刘栎杉,等.印度尼西亚 M_s≥7.8强震时空对称性特征及其趋势判断[J].自然灾害学报,2013,22(1):190-197.
[14]延军平,白晶,苏坤慧,等.对称性与部分重大自然灾害趋势研究[J].地理研究,2011,30(7):1159-1168.
[15]延军平,闫军辉,白晶,等.基于可公度方法的陕西及邻近地区重大自然灾害发生趋势探讨[J].灾害学,2010,25(2):18-20.
[16]延军平,闫娜.关于地震预测体系构建的可能性及验证[J].陕西师范大学学报:哲学社会科学版,2008,37(5):1159-1168.
[17]徐道一,王明太,耿庆国,等.翁文波院士的信息预测理论体系的创新性及其意义[J].地球物理学进展,2007,22(4):1375-1379.
[18]董国胜.地震预测与防灾减灾[M].北京:地震出版社.2001:95-98.
[19]杨蓉,延军平.对称性与宁夏地震灾害趋势判断[J].陕西师范大学学报:自然科学版,2012,40(6):92-96.
[20]李双双,延军平.西太平洋俯冲带北部地区Ms≥8强震时空对称性特征[J].地球物理学进展,2012,27(3):960-966.
[21]柳秀林.1951-2008年广西降水变化及对ENSO事件的响应初探[J].科技资讯,2011,34:217.
[22]李秀存,李耀先,张永强.ENSO事件对广西气候影响的统计分析[J].广西气象,2000,21(2):21-25.
[23]吴梦初,延军平,刘栎杉.甘肃省雨涝灾害时间对称性及趋势判断[J].干旱区资源与环境,2014,28(8):125-131.
[24]杨马陵,塔青.太阳黑子活动与新疆强震活动的关系[J].内陆地震,2012,26(1):10-16.
[25]张玲玲,董婕,延军平,等.对称性与西藏南部Ms≥6.6 级地震趋势判断[J].高原地震,2012,24(3):1-5.

