Hull-White利率模型仿真与债券估值
陈 勇,邓 坤
(湖南大学 金融与统计学院,湖南 长沙 410079)
Hull-White利率模型仿真与债券估值
陈 勇,邓 坤
(湖南大学 金融与统计学院,湖南 长沙 410079)
应用Vasicek模型和Nelson-Siegel模型估计Hull-White利率模型的参数,运用蒙特卡洛方法模拟利率路径,根据利率路径估计中国国债的价值,并进行敏感性分析.结果表明,运用蒙特卡洛方法模拟Hull-White利率模型,具有计算简单和运算速度快的特点,且债券估值的结果较为精确.该方法可广泛地应用于债券及其衍生品的定价分析.
利率期限结构;Hull-White模型;蒙特卡洛
1 引 言
利率期限结构是某个时点上债券的到期期限与收益率之间的关系.利率期限结构模型是资产定价、衍生品设计和利率风险管理的基础性问题.在利率市场化背景下,对利率期限结构的研究可以为债券的定价提供理论依据,促进债券及其衍生品的发行和交易,并为度量和管理利率风险提供工具和手段.
利率期限结构模型可以分为静态模型和动态模型.静态模型考虑某个时点上不同到期期限的债券收益率,应用样条函数拟合整条利率曲线.动态模型应用随机过程刻画利率波动.动态模型根据随机因子的个数可以分为单因子模型、双因子模型和多因子模型.单因子模型应用单因子扩散过程刻画即期利率的动态变化.由于单因子模型的参数估计简单,往往可以求出解析解,应用最为广泛.
Vasicek(1977)[1]应用均值回归的扩散过程描述即期利率的波动,是最早的单因子模型.为了克服Vasicek模型名义利率可能为负的缺点,Cox、Ingersoll & Ross(1985)[2]提出了均值回归的平方根扩散过程CIR模型.后来,Chan et al(1992)[3]将各种形式的单因子模型归纳为CKLS模型.
各种单因子扩散模型在很大程度上揭示了利率波动的水平效应和均值回归特征,但是不能反映初始时期利率曲线的形状对未来即期利率的影响.Hull & White(1990)在Vasicek模型中引入了初始时期的利率曲线,反映了初始时期经济环境对未来即期利率的影响[4].
由于Hull-White模型的参数包含初始时期的利率曲线,数值模拟的难度较大,相关研究成果较少.已有文献主要应用三叉树方法对Hull-White模型进行离散化处理,并对债券及其衍生品进行定价分析.Hull & White(1994,1996)提出了分解Hull-White模型的三叉树方法[5,6].宋逢明和石峰(2006)应用三叉树方法模拟了银行间债券市场的利率波动[7].石峰(2008)应用三叉树方法对信用衍生品进行定价分析[8].
已有文献主要采用三叉树方法分解Hull--White模型,缺乏应用蒙特卡洛方法的研究成果.本文首先估计Hull-White模型的参数,然后应用蒙特卡洛方法模拟Hull-White模型下的利率波动,并根据利率路径估计无风险债券价格,最后进行了敏感性分析.
2 研究思路
Hull-White模型的随机微分方程为
drt=k(θt-rt)dt+σdBt,
其中,rt是即期利率,k是即期利率向长期平均水平收敛的速度,σ为即期利率波动的标准差,Bt是标准的维纳过程,θt是长期平均即期利率,且
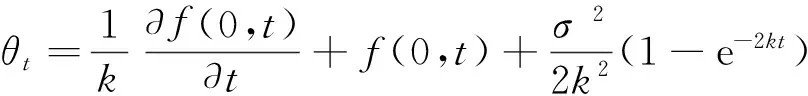
其中,f(0,t)是初始时期的利率曲线隐含的t时刻之后的远期利率.
先估计Hull-White模型的参数,再应用蒙特卡洛方法模拟Hull-White模型下的利率波动,并估计债券价值.分两步估计Hull-White模型的参数:
1)应用Vasicek模型估计参数k和σ;
2)应用Nelson-Siegel模型(NS模型)估计初始时期的远期利率f(0,t)和θt.蒙特卡洛模拟和债券估值分为以下步骤:
1)对Hull-White模型进行变量变换并模拟利率路径rt;
2)应用利率路径rt对债券的现金流进行贴现,从而可以得到债券的价格;
3)敏感性分析.分析债券估值结果对参数k和σ的敏感性.
3 Hull-White模型及其参数估计
先应用Vasicek模型估计参数k和σ,再应用NS模型估计初始时期的利率曲线参数f(0,t)和θt.
3.1 Vasicek模型求解及其参数估计
Vasicek模型的随机微分方程为
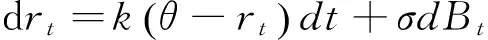
其中,rt是即期利率,k表示即期利率向长期平均水平收敛的速度,θ表示长期平均即期利率,σ为即期利率波动的标准差,Bt是标准的维纳过程.
将Vasicek模型转换为OU过程,再对OU过程求解.令xt=rt-θ,代入Vasicek模型,可以得到标准OU过程
dxt=-kxtdt+σdBt.
OU过程的解为
(1)
将xt=rt-θ代入式(1),整理可得
(2)
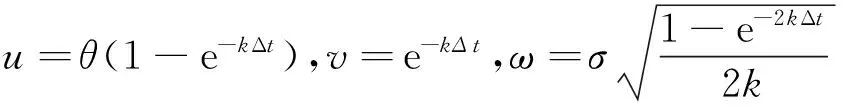
rt+Δt=u+vrt+ωη,η~N(0,1).
(3)
搜集银行间债券市场的相关数据,应用普通最小二乘方法进行回归分析,可以得到参数u,v和ω的估计值,再得到Vasicek模型的参数估计值k和σ.
3.2 远期利率估计
NS模型设定的远期利率公式为
(4)
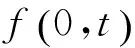
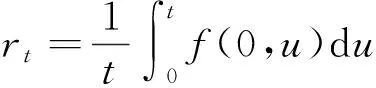
从而得到即期利率为
(5)
已知即期利率rt,贴现因子D(t)可以表示成D(t)=e-rtt.设Ci,ti分别为无风险债券的第i笔现金流的金额和到期期限,则债券价格

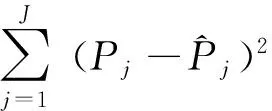
可以得到β0,β1,β2和τ的估计值.
4 Hull-White模型仿真
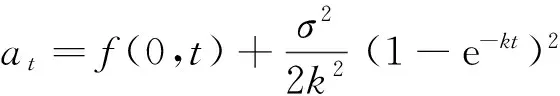
dxt=-kxtdt+σdBt.
先应用蒙特卡洛方法模拟得到xt,再根据rt=xt+at得到利率路径rt,最后应用利率路径rt对债券的现金流进行贴现,从而可以得到无风险债券的价格.
5 参数估计和债券估值
5.1 Hull-White模型参数估计结果
选取期限为1个月的上海银行间同业拆借利率估计Vasicek模型的参数.样本期间从2008年1月至2013年11月,共71个月度数据.由于均值回归过程属于平稳过程,先检验样本数据的平稳性.ADF检验结果显示样本数据为平稳过程,再依据式(3)进行回归分析.回归结果如表1所示.

表1 Vasicek模型的参数估计结果
应用NS模型拟合2013年11月1日的交易所的国债利率曲线.搜集了2013年11月1日有交易价格的14只样本债券,应用高斯牛顿迭代法估计NS模型,最小化样本债券的理论价格与市场价格的差额的平方和.NS模型的参数估计结果如表2所示.

表2 2013年11月1日NS模型的参数
5.2 债券估值结果与敏感性分析
我们选取2013年11月1月在上海证券交易所流通的八只附息票国债作为研究对象,债券代码分别为019307、010501、010603、019315、010512、010107、010303、010706.用蒙特卡洛方法模拟利率路径,再用利率路径对债券的现金流进行贴现,并将债券的估计价格和当天的实际收盘价进行比较.利率模拟的次数为1 000次.8只债券的估值结果如表3所示.
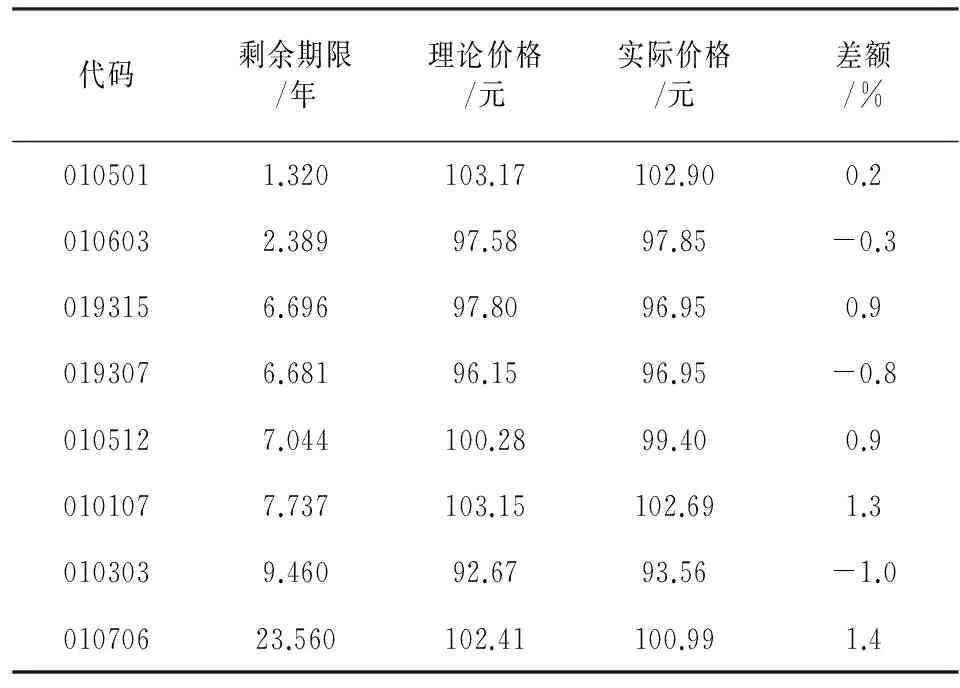
表3 样本国债价格的预测结果
从总体上看,Hull-White利率模型对8只债券的估值结果较为精确,特别是到期期限较短的债券,理论价格与实际价格误差不超过0.9%.究其原因,债券的到期期限越短,交易越活跃,债券的流动性越好,实际价格的波动越小.与三叉树方法相比,蒙特卡洛方法具有实现过程简单和运算速度快的特点,并且不存在模型偏误.
选取代码为010603的债券分析估值结果对参数k和σ的敏感性.从总体上看,债券价格与参数k和σ的变动方向符合预期,但是债券价格对参数变动不敏感.首先,当均值回归速度k上升时,债券的价格上涨.当k增长时,即期利率向较高的远期利率的收敛速度加快,导致即期利率水平上升,债券的价值趋向于下降.同时,当k增长时,在其他参数不变的情况下,即期利率的波动方差上升,由于债券价格是即期利率波动方差的增函数,债券的价值趋向于上升.由于两种作用相互抵消,导致债券价值对k的变动不敏感.其次,当即期利率的波动标准差σ上升时,债券的价格上升.由于债券价格是即期利率的凸函数,因此,即期利率的波动越大,债券的价格越高.
6 结 论
分别应用Vasicek模型和NS模型估计Hull-White利率模型的参数,再对即期利率进行变量变换,并运用蒙特卡洛方法模拟利率路径,最后应用利率路径贴现债券的现金流,并分析债券估值对Hull-White模型参数的敏感性.结果表明,运用蒙特卡洛方法模拟Hull-White利率模型,具有计算简单和运算速度快的特点,且债券估值的结果较为精确.由于Hull-White模型既考虑利率波动的特征,又反映初始时期利率曲线的影响,该方法可广泛地应用于债券及其衍生品的定价分析.
[1]OVASICEK.Anequilibriumcharacterizationofthetermstructure[J].JournalofFinancialEconomics, 1977,5 (2): 177-188.
[2]JCCOX,JEINGERSOLL,SAROSS.Atheoryofthetermstructureofinterestrates[J].Econometrica, 1985, 53(2): 385-407.
[3]KCCHAN,GAKAROLY,FALONGSTAF,etal. An empirical comparison of alternative models of the short term interest rate[J]. Journal of Finance, 1992, 47(3): 423-455.
[4] J HULL, A WHITE. Pricing interest rate derivative securities[J]. Review of Financial Studies, 1990, 3(4): 573-592.
[5] J HULL, A WHITE. Numerical procedures for implementing term structure models: single-factor models[J]. Journal of derivatives, 1994 (1): 7-16.
[6] J HULL, A WHITE. Using hull-white interest rate trees[J]. Journal of Derivatives, 1996, 3(3): 26-36.
[7] 宋逢明,石峰.基于Hull-White模型的债券市场利率期限结构研究[J].运筹与管理,2006(3):34-36.
[8] 石峰.Hull-White模型在次级债定价中的应用研究[J].运筹与管理,2008(5):108-122.
Simulation of Hull-White Model and Bond Pricing
CHEN Yong, DENG Kun
(College of Finance and Statistics, Hunan University, Changsha, Hunan 410079, China)
This paper used the Vasicek model and the Nelson-Siegel model to estimate the parameters of Hull-White model,and simulated the Hull-White term structure model. The theoretical prices of sample bonds were priced through the Monte Carlo simulation methods. We conducted a sensitivity analysis. It is shown that simulation-based method is more precise than the three-tree one to price bonds.
term structure of interest rates; Hull-white model; Monte Carlo simulation
2015-10-15
湖南省自然科学基金资助项目(14JJ2054)
陈 勇(1972—),男,湖南醴陵人,副教授,博士
E-mail: leochen007@hotmail.com
F830.91
A

