具有度限制条件的IC平面图类中轻3－圈的存在性

田京京，聂玉峰

（1西北工业大学理学院，陕西西安710129；

2陕西理工学院数学与计算机科学学院，陕西汉中723000）

具有度限制条件的IC平面图类中轻3－圈的存在性

田京京1，2，聂玉峰1

（1西北工业大学理学院，陕西西安710129；

2陕西理工学院数学与计算机科学学院，陕西汉中723000）

利用权转移方法证明了每个最小度至少为5并且最小边度至少为11的IC－平面图G含有一个最大度max｛d（u），d（v），d（w）｝≤17的3－圈。

IC－平面图；权转移方法；3－圈

本文仅考虑简单的有限无向图。设G是一个平面图，分别用V（G）、E（G）、F（G）、Δ（G）、δ（G）来表示它的点集合、边集合、面集合、最大度和最小度。特别地，G中任意一条边uv所关联的点u、v度的和d（u）+d（v）称为边uv的度。用k－、k+－和k－－点或面分别表示一个点或面的度为k、至少为k和至多为k。其余定义若无特殊说明，均参考文献［1］。

一个图称为是1－平面的当且仅当它可以画在一个平面上使其任何一条边最多交叉另外一条边。1－平面图是Ringel［2］于1965年研究平面图的点－面染色时提出来的，至今还有许多未被研究的问题。

设G为一个图在平面上的一个嵌入，如果图G上存在交叉点，则必然是G的某两条边交叉产生的，于是G中的每个交叉点c都可以与G中的4个顶点（即两条交叉边上的4个顶点）所构成的点集建立对应关系，称这个对应关系为S。显然，在一个好的1－平面图画法（即交叉点最少的画法）中，对于任意两个交叉点c1、c2存在｜S（c1）∩S（c2）｜≤2。据此，定义1－平面图的两个子类，若满足｜S（c1）∩S（c2）｜＝0，则称该1－平面图为IC－平面图，若｜S（c1）∩S（c2）｜≤1，则称该1－平面图为NIC－平面图。IC－平面图的概念是由文献［3］于2010年提出的，他们证明了每个IC－平面图都是5－可染的，并且色数的上界5是紧的。NIC－平面图的概念则是由文献［4］于2014年提出的，其中给出了完全多部图的NIC－平面性与IC－平面性的完全刻画。

设H是一个连通图，G是一个图类，K是一个给定的图。如果任意的图G∈G都包含一个与图K同构的子图H，其在图G中的最大度是一个不超过某个与图G的选择无关的常数，则称图K在图类G中是轻的。寻找给定图类中轻的子图是图结构理论中的一类经典问题。例如，文献［5］得出一个著名的结论：任何一个最小度至少为5的平面图包含一个3－圈xyz，其满足max｛d（u），d（v），d（w）｝≤17，并且该结论中的上界17是最优的。文献［5］的定理说明：3－圈在最小度至少为5的平面图类中是轻的。2014年，文献［6］证明了3－圈在最小度至少为5并且最小边度至少为12的1－平面图类中是轻的，并提出如下猜想：

猜想 3－圈在最小度至少为5并且最小边度至少为11的1－平面图类中是轻的。

本文将证明猜想对于1－平面图的子类IC－平面图是成立的。

1 主要定理及其证明

设G是IC－平面图。如果将G中的所有交叉点全部看成是4度点，则可以得到一个交叉数为0的图，即平面图G×，下面称图G×为G的关联图。设v是图G×中的的一个点，如果v∈V（G×）＼V（G），则称v是G×的一个假点或称v是G的一个交叉点。如果图G×的一个面f关联至少一个假点，则称f为G×的一个假面，否则称f为G×的一个真面。设v是G×中的k－点，v1、v2、…、vk是v在G×中按顺时针排列的所有邻点。在G×中与边vvi和vvi+1关联的面记为fi，其中1≤i≤k，并记vk+1∶＝v1。

定理 每个最小度至少为5并且最小边度至少为11的IC－平面图含有一个3－圈xyz，其满足max｛d（u），d（v），d（w）｝≤17。

证明 设G是定理1的反例，G×是G的关联图。给G×中的每个点v赋初始权值c（v）＝d（v）－6，同时给G×中的每个面f赋初始权值c（f）＝2d（f）－6，运用平面图G×上的欧拉公式，有

现在，按照如下规则对V（G×）∪F（G×）上的所有元素重新分配权值。

（1）G×中每个18+－点向它所关联的面转移；

（2）设f＝xyz是G×中的一个3－面，且x是一个18+－点。

（2.1）若y和z是5－－点，则f向y、z分别转移。

（2.2）若y是一个18+－点且z是4－点或5－点，则f向z转移。

（2.3）若y是一个4－点或5－点且z是一个度介于6与17之间的点，则f向y转移。

（3）每个4+－面向它关联的4－点转移1，每个4+－面向它关联的5－点转移。

设c′（x）为元素x∈V（G×）∪F（G×）在应用以上权转移规则后得到的新权值，下面证明对于每个x∈V（G×）∪F（G×）都有c′（x）≥0。因此，矛盾。

设f∈F（G×），若d（f）＝3，则由（1）和（2）知c′（f）＞0。若4≤d（f）≤5，则根据IC－平面图的定义知f至多关联1个4－点。另一方面，由于G的最小边度至少为11，故f至多关联2个5－点，从而由（3）可得

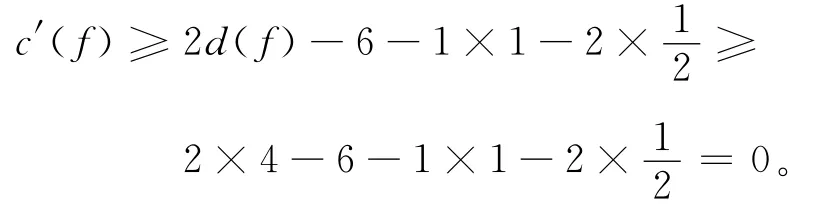
若d（f）≥6，则由（3）可得

c′（f）≥2d（f）－6－d（f）＝d（f）－6≥0。

设v∈V（G×）。若d（v）≥18，则由（1）得

根据规则（1）—（3），图G×中介于6到17度的点不参与权转移，因此若6≤d（v）≤17，则必有

c′（v）＝c（v）＝d（v）－6≥0。

设d（v）＝4。若v至少关联2个4+－面，则由（3）可得

c′（v）≥4－6+2×1＝0。

若v仅关联1个4+－面，不妨设其为f1，则f2、f3与f4均为3－面。若v3是5－点，则v2与v4中必有一个18+－点，否则图G中的3－圈v2v3v4即为所求。不妨设v2是18+－点，从而根据（2.2），f2向v转移，于是再结合（3）可得因此，可假设v3是6+－点。同时，由对称性可知，v4也是6+－点。由于图G不含该待证定理中所述的轻3－圈，故v1与v2必为18+－点，从而根据（2.2）与（2.3），f2与f4分别向v转移至少。最后再结合（3），可得

若v仅关联3－面，即f1、f2、f3与f4均为3－面。由于G是一个反例，v1、v2、v3与v4中必至少有2个18+－点。根据对称性，考虑两种情况。首先假设v1与v2是18+－点。由于G的最小边度至少为11，v3与v4中至少有一个6+－点，不妨假设d（v3）≥6。则由（2.2）与（2.3），f1向v转移，f2向v转移至少，于是有

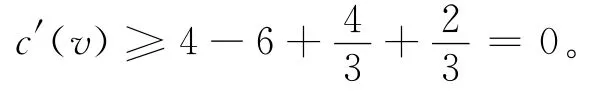
其次，假设v1与v2是18+－点。由于v2v4∈E（G），v2与v4中必有一个6+－点，不妨设d（v2）≥6。则由（2.2）与（2.3），f1与f2分别向v转移至少，由（2.1）—（2.3），f3与f4分别向v转移至少。因此有

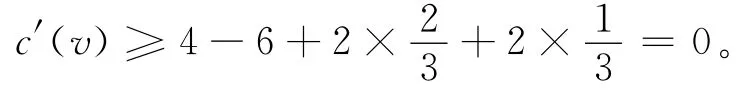
设d（v）＝5。若v至少关联2个4+－面，则由（3）可得

若v只关联1个4+－面，不妨设其为f1，则f2、f3、f4与f5均为3－面。由图G的IC－平面性，f2、f3、f4与f5中必有一个是真3－面，不妨假设是f2，由于反例图G的最小边度至少为11，故v2与v3均为6+－点，并且二者之间必有一个18+－点，于是由（2.2）与（2.3）知f2向v转移至少。此时考虑f1，由（3）得

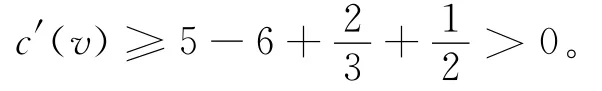
若v关联的全是3－面，则在G×中v与最多一个4－点相邻，否则与图G的IC－平面性矛盾。这说明f1、f2、f3、f4与f5中至少有3个是真3－面。由于G是反例，G×中的每个真3－面都关联至少一个18+－点，于是由（2.1）—（2.3）知每个与点v关联的真3－面向v转移至少。因此，

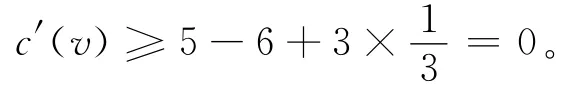
2 结论

本文利用权转移的方法证明文献［6］提出的猜想对于1－平面图的子类IC平面图成立，且IC平面图G含有一个最大度max｛d（u），d（v），d（w）｝≤17的3－圈。

［1］Bondy J A，Murty U S R.Graph theory with applications［M］.New York：North－Holland，1976.

［2］Ringel G.Ein sechsfarbenproblem auf der Kugel［J］.Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg，1965，29：107－117.

［3］Kral D，Stacho L.Coloring plane graphs with independent crossings［J］.Journal of Graph Theory，2010，64（3）：184－205.

［4］Zhang X.Drawing complete multipartite graphs on the plane with restrictions on crossings［J］.Acta Mathematica Sinica，2014，30（12）：2045－2053.

［5］Borodin O V.Solution of problems of Kotzig and Gruunbaum concerningthe isolation of cycles in planar graphs［J］.Mathematical Notes，1989，46：835－837.

［6］Zhang X.Light 3－cycles in 1－planar graphs with degree restrictions［J］.Bulletin of the Korean Mathematical Society，2014，51（2）：511－517.

〔责任编辑 宋轶文〕

Light 3－cycles in IC－planar graphs with degree restrictions

TIAN Jingjing1，2，NIE Yufeng1
（1School of Natural and Applied Sciences，Northwestern Polytechnical University，Xi′an 710129，Shaanxi，China；2School of Mathematics and Computer Science，Shaanxi University of Technology，Hanzhong 723000，Shaanxi，China）

It is proved by discharging method that every IC－planar graph Gwith minimum vertex degree at least 5and minimum edge degree at least 11contains a 3－cycle xyz with max｛d（u），d（v），d（w）｝≤17.

IC－planar graph；discharging method；3－cycle

05C10

O157.5

A

1672－4291（2015）05－0001－03

10.15983／j.cnki.jsnu.2015.05.151

2015－03－19

国家自然科学基金（11301410，11461038）

田京京，女，副教授，博士研究生，主要研究方向为图论及组合优化。E－mail：tianjingjing2004＠163.com