大直径钢护筒嵌岩桩水平承载特性有限元分析

温 海 峰

(广东省路桥建设发展有限公司，广东 广州 510623)

大直径钢护筒嵌岩桩水平承载特性有限元分析

温 海 峰

(广东省路桥建设发展有限公司，广东 广州 510623)

通过有限元法研究了大直径钢护筒嵌岩桩的水平承载特性，根据桩顶荷载—位移曲线、桩身水平位移曲线和桩身弯矩的计算结果，分析了钢护筒对大直径嵌岩桩水平承载力的影响，探讨了嵌岩桩嵌岩深度、桩径、钢护筒嵌岩深度、钢护筒壁厚以及地基岩体强度参数对嵌岩桩水平承载力的影响，得出了一些有价值的结论。

钢护筒嵌岩桩，嵌岩深度，水平承载力，有限元法

码头工程中的桩基础除了承受竖向荷载外，同时还需承受系缆、船舶撞击、水流、风以及地震等引起的水平荷载。目前，国内外学者对于嵌岩桩的研究已不少，但关于水平荷载作用下大直径嵌岩桩承载性状的研究相对较少，尤其对于水上大直径钢护筒嵌岩桩工作性状的研究更少。在水上施工嵌岩桩需要架设钢护筒，钢护筒作为施工措施需嵌入岩层一定深度，施工完成后钢护筒被保留下来与桩身混凝土共同承受荷载作用。现有桩基规范的设计计算中一般不考虑钢护筒参与受力，但是由于钢护筒具有较大的抗弯刚度，其在水平荷载作用下必然会承受荷载[1]。

本文结合重庆果园码头桩基原型资料，通过有限元方法研究水平荷载作用下大直径钢护筒嵌岩桩的受力变形机理，分析了钢护筒对大直径嵌岩桩水平承载力的影响，讨论了钢护筒嵌岩桩水平承载力受嵌岩深度、桩径、钢护筒嵌岩深度、钢护筒壁厚以及地基岩体强度参数的影响。

1 有限元分析方法

1.1 有限元模型

本文选取重庆果园港二期扩建工程的嵌岩灌注桩为原型建立有限元模型。有限元软件应用ABAQUS建立钢护筒嵌岩单桩的计算模型。由于模型具有对称性，故取整个模型的一半建立了三维有限元模型，为了保证数值计算的精度，同时满足边界条件，模型的影响范围水平方向取20倍桩径，桩底以下取2倍桩长。嵌岩桩桩基总长21 m，桩径2 200 mm，其中地面以上取10 m，嵌入中等风化岩石11 m，桩身外套钢护筒，钢护筒长12.75 m，地面以上10 m，其中钢护筒嵌入中等风化岩石2.75 m，钢护筒壁厚16 mm，假定地基为各向同性均质的中等风化岩石，桩身混凝土、钢护筒、地基岩体均采用C3D8R实体单元。建模时，钢护筒顶面与混凝土桩身顶面齐平，在靠近嵌岩桩的区域细化网格，远离嵌岩桩区域的网格逐渐变疏，有限元计算模型及网格划分见图1。在对称面xz上施加对称边界条件，地基底面约束x，y，z三个方向上的位移，地基侧面约束x，y方向上的位移。

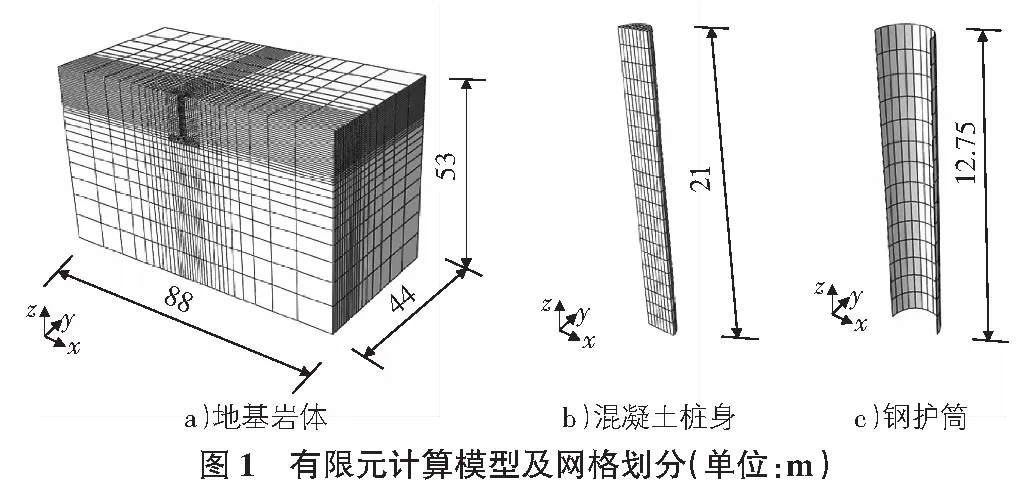
1.2 材料本构模型

模型中的钢护筒采用弹性—强化模型，即在钢材应力未达到屈服应力fy之前应力—应变曲线的斜率为钢材的弹性模量Es，屈服之后简化为斜率为0.01Es的直线。假定钢护筒密度ρs=7 850 kg/m3，弹性模量Es=206 GPa，弹性阶段的泊松比vs=0.3，屈服强度fy=235 MPa。

桩身混凝土采用塑性损伤模型，假定混凝土密度ρc=2 500 kg/m3，弹性模量Ec=30 GPa，弹性阶段的泊松比vc=0.2，轴心抗压强度fc=20.1 MPa，轴心抗拉强度fy=2.01 MPa。

混凝土单轴应力—应变关系采用以下公式[2]确定：

受压：

σ=(1-dc)Ecεc

(1)

受拉：

σ=(1-dt)Ecεt

(2)

其中，εc，εt为与抗压、抗拉强度相对应的峰值应变；dc，dt为单轴受压、受拉损伤演化参数，具体取值见文献[2]。

地基岩体采用摩尔—库仑模型，参照重庆地区试验数据[3]和工程岩体分级标准[4]，地基岩体的基本参数取为：弹性模量Er=3 GPa，泊松比vr=0.3，粘聚力c=400 kPa，摩擦角φ=30°，密度ρr=2 500 kg/m3。

1.3 接触面模型

建立有限元计算模型时，除了考虑桩周岩体、桩身混凝土和钢护筒的材料非线性外，同时考虑了桩—岩相互作用以及钢护筒与桩身混凝土间的相互作用。在ABAQUS[5]中通过接触命令“contact pair”实现接触的设置，接触面上的本构关系法向采用硬接触，切向采用库仑弹塑性摩擦模型，以罚函数法模拟。接触面采用主—从算法，计算模型中涉及3种接触面，其中钢护筒与桩身混凝土的接触对中，钢护筒为主控面，混凝土为从属面，摩擦系数取0.5[6]；钢护筒与岩石的接触对中，钢护筒为主控面，岩石为从属面，摩擦系数取0.4；混凝土与岩石的接触对中，混凝土为主控面，岩石为从属面，摩擦系数取0.35[7]。

2 大直径钢护筒嵌岩桩水平承载性状

为了研究水平荷载作用下大直径钢护筒嵌岩桩的承载性状，分别建立了有钢护筒和无钢护筒的模型，以便对比研究，桩顶自由，在桩顶施加水平荷载。

2.1 桩顶荷载—位移曲线

图2给出了无钢护筒和有钢护筒的嵌岩桩桩顶荷载—位移曲线，有钢护筒时水平力加载至2 000 kN，无钢护筒时水平力加载到800 kN时桩基已发生破坏。当有钢护筒时，桩顶荷载—位移曲线在水平荷载2 000 kN内为缓变型曲线，相比无钢护筒时嵌岩桩的水平承载力得到了提高。以水平力加载至600 kN为例，无钢护筒嵌岩桩的桩顶位移为18.26 mm，有钢护筒嵌岩桩的桩顶位移仅为10.32 mm，考虑钢护筒后水平位移减少了约43.5%。

2.2 桩身水平位移

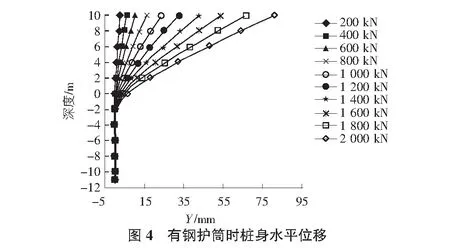
由图3和图4可知，桩身的水平位移随水平荷载的增大而增大，在各级荷载作用下桩顶处的位移最大，由桩顶自上而下水平位移逐渐减小，由于地面(深度为0 m)以上的自由段较长，到达地面时水平位移已经很小，嵌岩段的水平位移量值较小，说明嵌岩桩的嵌固作用明显。考虑钢护筒后，其能有效地约束地面以上桩身的水平位移。

3 水平承载性状主要影响因素

3.1 桩径的影响

分别取嵌岩桩桩径为1 800 mm～2 600 mm的情况进行了有限元计算。当嵌岩桩桩径为1 800 mm时，水平荷载加载到2 000 kN时对应的桩顶水平位移已达1 674 mm，为了方便比较一律取水平荷载为1 800 kN时的情况进行比较。图5给出了不同桩径下桩身的水平位移曲线。由图5可以看出，桩径对水平承载力的影响较大，随桩径的增大，嵌岩桩的水平承载力增大，可见桩径对钢护筒嵌岩桩水平承载力影响较大，在实际设计中要综合考虑成本和承载力要求确定合理的桩径。

3.2 钢护筒嵌岩深度的影响

图6给出了2 000 kN水平荷载下不同钢护筒嵌岩深度下桩身的水平位移曲线，可以看出，桩顶水平位移随钢护筒嵌岩深度的增加而减小，钢护筒嵌岩深度从2.75 m增大到5.5 m，桩顶水平位移减小了约30%，说明钢护筒嵌岩深度增加2.75 m有效地提高了桩基的水平承载力，而从5.5 m增大到8.25 m，桩顶水平位移仅减小了2%，可见继续增加钢护筒嵌岩深度对提高桩基承载力已不明显。所以在实际施工过程中，要从经济效益和桩基最佳受力两方面综合考虑，确定合理的钢护筒嵌岩深度，钢护筒嵌岩深度的增大一方面增加了施工难度，一方面增大了投资成本，而且对承载力的提高在超过某一临界嵌岩深度后已无明显作用。

3.3 钢护筒壁厚的影响

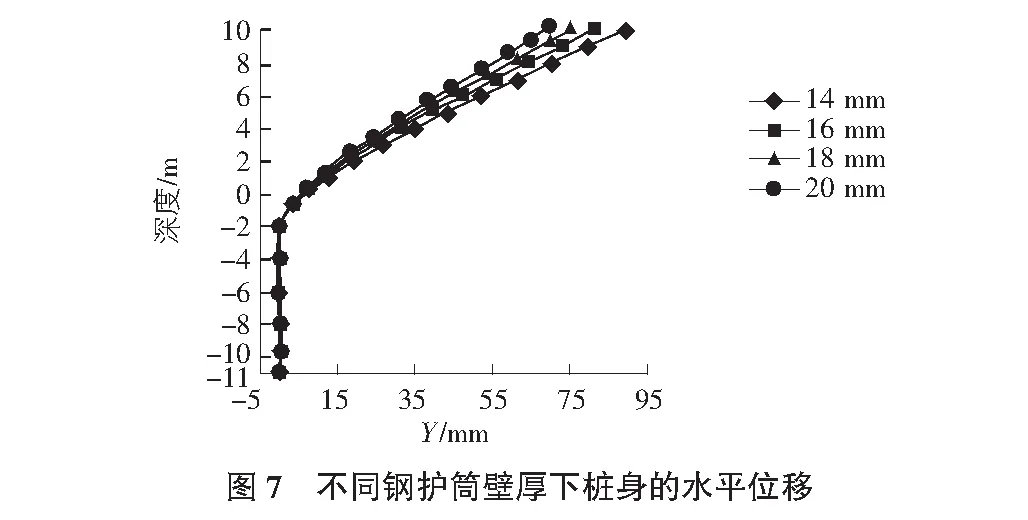
图7给出2 000 kN水平荷载下不同钢护筒壁厚下桩身的水平位移曲线，可以看出，钢护筒对水平承载力的影响较大，随钢护筒壁厚的增大，桩顶的水平位移减小，说明钢护筒的壁厚对桩身抵抗弯曲变形有作用，且钢护筒壁厚越大，作用越大。

4 结语

本文结合实际工程原型资料通过有限元非线性计算，研究了水平荷载作用下码头大直径钢护筒嵌岩桩的水平承载性状，得到了以下结论：

1)水平荷载作用下大直径钢护筒嵌岩桩的荷载—位移曲线呈缓变型，相比无钢护筒时嵌岩桩的水平承载力得到了提高，钢护筒能有效地约束地面以上桩身的水平位移。2)钢护筒嵌岩桩随嵌岩深度的增大，桩顶的水平位移减小，但是减小的幅值较小，钢护筒嵌岩桩存在临界嵌岩深度，超过该临界嵌岩深度后，仅靠增加嵌岩深度对提高桩基的水平承载力无明显贡献。3)桩径对钢护筒嵌岩桩水平承载力影响较大，随桩径的增大，嵌岩桩的水平承载力增大，在实际设计中要综合考虑成本和承载力要求确定合理的桩径。4)钢护筒嵌岩深度存在临界嵌岩深度，超过该临界深度后继续增加钢护筒嵌岩深度对提高桩基承载力已不明显。5)钢护筒对于桩身抵抗弯曲变形有作用，且钢护筒壁厚越大，作用越大。

[1] 美国各州公路和运输工作者协会.美国公路桥梁设计规范[M].北京：人民交通出版社，1998.

[2] GB 50010—2010，混凝土结构设计规范[S].

[3] 杨 凯，刘东升，易前应，等.重庆市岩石抗剪强度参数统计分析及应用[J].后勤工程学院院报，2008，24(2):18-24，36.

[4] GB 50218—94，工程岩体分级标准[S].

[5] ABAQUS Inc.Abaqus theory manual and user’s manual version 6.10[Z].Providence，R I：ABAQUS Inc.

[6] Baltay P，Gjelsvik A.Coefficient of friction for steel on concrete at high normal stress[J].Journal of Materials in Civil Engineering，1990，2(1):46-49.

[7] KHAN A.Numerical modeling of shear socketed piers[J].International Journal for Numerical and Analytical Methods in Geomechanics，2000，24(11)：853-867.

Finite element analysis on horizontal bearing capacity of large-diameter steel-casing rock-socketed pile

Wen Haifeng

(GuangdongHighway&BridgeConstructionDevelopmentCo.,Ltd,Guangzhou510623,China)

The thesis studies horizontal bearing features of large-diameter steel-casing rock-socketed pile through finite element method, analyzes the impact of steel-casing upon horizontal bearing capacity of large-diameter rock-socketed pile according to pile top displacement curve, horizontal pile displacement curve and pile bending moment, explores influence of rock-socketed pile depth, rock-socketed pile diameter, steel-casing rock-socketed depth, steel-casing rock-socketed wall thickness and foundation rock strength parameter upon horizontal bearing capacity of rock-socketed pile, and finally draws some valuable conclusions.

steel-casing rock-socketed pile, rock-socketed depth, horizontal bearing capacity, finite element method

2015-04-22

温海峰(1982- )，男，硕士，工程师

1009-6825(2015)19-0050-03

TU473.11

A