基于最大熵理论的多类型电动汽车充换电站规划

吴健生，李小舟

(1．北京大学深圳研究生院，城市人居环境科学与技术重点实验室，广东深圳518055; 2．北京大学城市与环境学院，地表过程与模拟教育部重点实验室，北京100871)

基于最大熵理论的多类型电动汽车充换电站规划

吴健生1，2，李小舟1

(1．北京大学深圳研究生院，城市人居环境科学与技术重点实验室，广东深圳518055; 2．北京大学城市与环境学院，地表过程与模拟教育部重点实验室，北京100871)

基于最大熵理论，提出一种多类型电动汽车充电站规划方法。本文在分析不同类型电动汽车充换电方式的特点后，定义电动汽车分布熵描述电动汽车充电站容量分布与充电负荷的重合程度，采用多目标方式建立多类型电动汽车充换电规划模型;定义不同目标的满意度函数，使用遗传算法对模型进行求解。最后，通过一个25节点的路网图，与仅考虑投资收益目标而不考虑均衡度的最小投资收益差法进行对比，说明了本文方法的有效性。

电动汽车;充电站规划;充电模式;最大熵

1 引言

电动汽车大规模代替传统汽车是解决气候与能源危机的一个有效途径［1］，而合理的电动汽车充电站规划，则是电动汽车普及的前提。

电动汽车充电站规划已经受到了国内外学者的广泛关注［2-6］。根据充电模式的不同，电动汽车充电站可以划分为换充、慢充和快充三种类型。

换充模式的充电站又称为电池组更换站，主要针对公交车、出租车等较大规模的统一标准车辆，对这种类型充电站的规划主要考虑地理信息(行驶路线、运行范围、充换电站服务半径等)、充换电需求、负荷预测、资金投入以及对电网削峰填谷作用等因素构造优化模型［2-5］。

慢充模式(即常规充电桩)可以在夜间低谷充电，主要满足私人汽车、政府及企事业单位用车的充电需求。空间布局上应在居民区、办公楼、社会停车场等安装充电桩，构建高覆盖率的充电网络，使车辆在停驶时可就近接入充电网络［2］。慢充模式的充电站规划需要满足城市整体规划和路网规划的要求，然后根据充电需求的分布和各区域电动汽车交通密度来考虑充电桩的网络分布，此外还需要充分考虑输配电网现状［7，8］。

快充模式则主要服务于私人汽车、政府及企事业单位用车在使用途中应急补电需求，在服务定位中应处于补充地位［2］。快充模式的充电站对电网冲击较大，在规划过程中需要重点考虑电网的承受能力［9］。

上述文献对不同类型的电动汽车充电站分别提出了大量的规划方法。实际上，随着电动汽车产业的不断发展以及标准充电站和电池组的确立，电动汽车用户可以自由选择不同的充电方式，对充电站的类型存在多样化的需求。因此，不同类型的充电站之间存在相互影响，在规划阶段需要协调考虑不同模式充电站的相互配合与补充，但是现有研究中都没有考虑不同类型充电站的相互协调。

通过充电电量、充电时间成本和充电站间最远距离的限制，可以使充电站容量分布与充电负荷在一定程度上得到重合［10，11］。但是现有研究都无法定量描述充电站容量分布与充电负荷的重合程度。

基于以上对不同充电模式的时间经济特性分析以及现有研究的不足，本文提出一种基于最大熵理论的多类型电动汽车充电站协调规划方法，主要优点包括:①考虑不同类型电动汽车充电站的特性，协调优化不同类型电动汽车充电站的布局;②定义充电站分布熵描述充电站容量与充电负荷的重合程度，建立多目标规划模型。

2 多模式电动汽车充电站协调规划模型

本节在综合考虑三种不同类型充电站的时间经济特性以及相互影响的基础上，引入充电站分布熵，建立多模式电动汽车充电站协调规划的多目标模型。建模的总体思路是:在保证充电需求满足要求、充电成本在可接受范围以内，希望找到投资收益比最佳并且分布合理的电动汽车规划方案。

2.1 目标函数

本文以投资成本与收益之差最小作为规划模型的第一个目标函数;同时定义充电站分布熵表征充电站分布与充电负荷的重合程度，以分布熵最大作为第二个目标函数。目标函数为:

式中，C为充电站投资与收益之差;Pij为第j个第i类充电站的规划容量;r0为贴现率;γi为第i类充电设施的折旧年限;为第j个第i类充电站的可能充电功率;Ri为第i类充电站的年收益率;E为期望值计算;H为电动汽车充电容量分布熵;PD，ij，pr为第j个充电站辐射区域内第i类充电负荷需求预测值; Fi为第i类充换电方式的投资函数，电动汽车的建设成本分为与功率相关的可变部分、与功率无关的固定部分:

式中，ai和bi分别为投资价格函数的系数。

在式(1)中，投资成本为三种类型充电站的年均投资成本之和以及电网冲击惩罚费用，收益则包括三种类型充电站的充电期望利润及附加收益。

式(2)所定义的分布熵反映充电站的规划功率与充电负荷需求的重合程度。充电站规划功率与充电负荷需求重合程度越大，则分布熵越大;反之，充电站规划功率与充电负荷需求重合程度越小，则分布熵也会越小。

2.2 约束条件

目标函数反应了电动汽车充电站投资和收益上的博弈以及对结果的目标性引导，即引导规划的结果在经济上达到最优同时考虑分布的均匀性。然而，在按照目标函数寻优的过程中，还需满足一定条件的约束，否则规划的结果将失去意义。

满足区域内电动汽车充电需求是进行电动汽车规划的基本要求，并且考虑未来的发展，需要留出一定的冗余度。不同类型充电站的总容量应大于预测的规划周期内最大充电需求，即:

式中，η为充电站建设冗余系数;PD，imax为规划期内区域内第i类充电负荷的最大值。

虽然在式(1)中考虑了充电站投资成本与收益的目标，但为了保证投资成本在可以承受的范围之内，仍需设置每类充电站的投资上限:

式中，Mimax为第i类充电站的投资上限。

3 基于满意度决策的多目标遗传算法

第2节中建立的模型是同时包含离散变量与连续变量的复杂的多目标优化问题，本文采用遗传算法进行求解。

3.1 个体满意度

在2.1节提出的两个目标具有不同的量纲，为了便于比较，定义经济满意度与分布熵满意度如下:

式中，sc，l和sh，l分别表示个体l的经济满意度与分布熵满意度;cl、cmax、和cmin分别表示个体l的投资收益差、种群内最大投资收益差和种群内最小投资收益差;hl、hmax和hmin分别表示个体l的分布熵、种群内最大分布熵和种群内最小分布熵。最终以sl作为个体l的满意度用作遗传算法选择操作的依据，α为满意度权重系数。

式(6)表示投资收益差最小时，满意度最大(等于1);投资收益差最大时，满意度为0;满意度随投资收益差由大到小在区间［0，1］中逐渐增加。式(7)表示分布熵最小时，满意度最小(等于0);分布熵最大时，满意度为1;满意度随分布熵由小到大在区间［0，1］中逐渐增加。式(6)和式(7)将目标函数式(1)和式(2)转换到统一的尺度去评价，为3.2节遗传算法适应度函数值的计算奠定了基础。

3.2 遗传算法的计算流程

对每个个体根据式(6)～式(8)计算满意度后，判断是否满足所有约束条件，对不满足约束条件的个体添加惩罚项，即可计算所有个体的适应度函数值;进而可以进行遗传算法的选择、变异、交叉操作，生成下一代个体，不断循环上述过程，直至找到最优个体。具体的计算流程如图1所示。

图1 遗传算法计算流程Fig．1 Flow chat of GA

4 算例分析

为了说明本文方法(负荷均衡法)的有效性，本节给出了仅考虑投资收益目标的规划方法(最小投资收益差法)与本文方法进行电动汽车充电站规划时在经济性、充电站分布均衡性两个方面的对比，分析本文方法规划结果的优点。

规划所采用的网络如图2所示［10］，图中圆圈的大小表征相应节点的充电负荷大小，本文假设为该节点的预测充电功率需求，路段上的数字表示两节点间的距离。其中，权重为134及107的节点假设为换电站的备选节点，权重为80和54的节点作为慢充备选节点，其余节点作为快充的备选节点。充换电站的成本参数由表1给出。

图2 计算路网Fig．2 Road network

表1 充换电站规划基础数据Tab．1 Basic data for electric vehicle charging stations planning

计算均衡度的对比如图3和表2所示。可以看出，本文方法的结果中，充电站的布局比重比较接近，说明电动汽车充电站的分布与充电负荷的重合性较好，而最小投资收益差法的计算结果则较本文方法分散。最小投资收益差法均衡度的方差为0.023，本文方法均衡度的方差为0.012，降低了45.5%。这是因为本文的模型引入了分布熵表征电动汽车充电站容量分布与充电负荷的重合程度，并以其最大作为电动汽车规划模型的一个目标，使得规划结果能够确保充电站容量分布与充电负荷的一致性。

图3 规划均衡度对比Fig．3 Equilibrium degree of planning

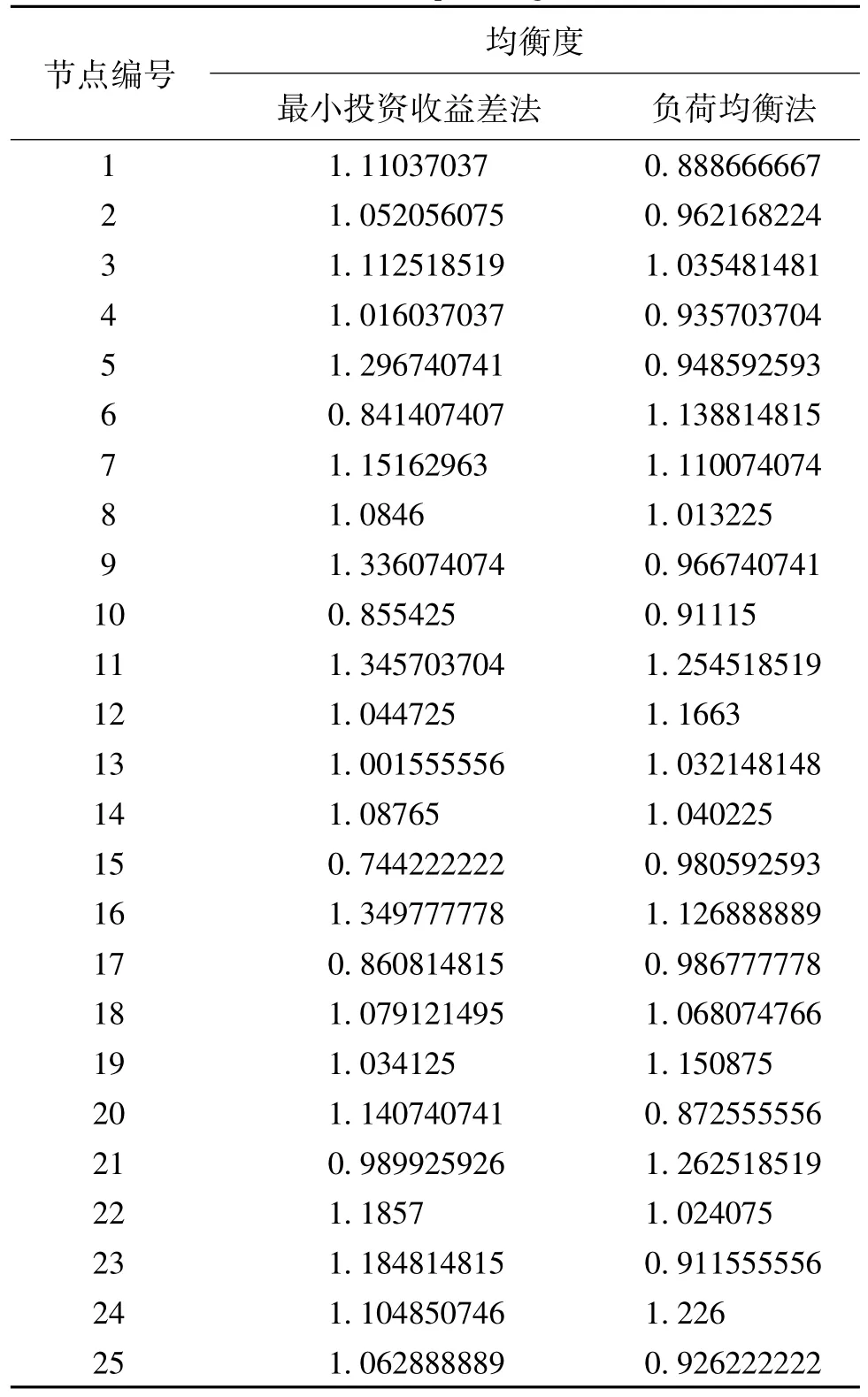
表2 充换电站规划结果均衡度Tab．2 Equilibrium degree results of vehicle charging stations planning

5 结论

本文基于最大熵理论提出了一种多类型电动汽车充换电站的规划方法，通过定义分布熵来描述充换电站与充电负荷的重合程度，以其最大化作为一个目标建立规划模型。

通过25节点路网系统的仿真分析表明，本文方法能够在考虑规划方案经济性的同时，得到与充电负荷重合程度较高的充换电站规划结果，具有较大的实用价值。

［1］吴万禄，韦钢，李作明，等 (Wu Wanlu，Wei Gang，Li Zuoming，et al．)．城市电动汽车充电站的规划(Planning of urban electric vehicles charging stations)［J］．电力与能源 (Power＆Energy)，2013，34(6):642-646．

［2］徐志丹(Xu Zhidan)．充换电设施在城市电网中的规划与建设(Planning and construction of electric charging facilities in the city grid)［J］．电气应用(Electrotechnical Application)，2013，(suppl．):130-133．

［3］葛少云，冯亮，刘洪，等(Ge Shaoyun，Feng Liang，Liu Hong，et al．)．考虑用户便捷性的电动汽车充电站规划 (Planning of electric vehicle charging stations considering users’convenience)［J］．电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2014，33(2):70-75．

［4］钱斌，石东源，谢平平，等 (Qian Bin，Shi Dongyuan，Xie Pingping，et al．)．电动公交车换电站－电池充电站优化规划 (Optimal planning of battery charging and exchange stations for electric vehicles)［J］．电力系统自动化(Automation of Electric Power Systems)，2014，38 (2):64-69，80．

［5］所丽，唐巍，白牧可，等 (Suo Li，Tang Wei，Bai Muke，et al．)．考虑削峰填谷的配电网集中型充电站选址定容规划 (Locating and sizing of centralized charging stations in distribution network considering load shifting)［J］．中国电机工程学报 (Proceedings of the CSEE)，2014，34(7):1052-1060．

［6］陈光，毛召磊，李济沅．等(Chen Guang，Mao Zhaolei，Li Jiyuan，et al．)．计及碳排放的电动汽车充电站多目标规划(Multi-objective optimal planning of electric vehicle charging stations considering carbon emission)［J］．电力系统自动化 (Automation of Electric Power Systems)，2014，38(17):49-53，136．

［7］Etezadi A M，Choma K，Stefani J．Rapid-charge electricvehicle stadions［J］．IEEE Transactions on Power Delivery，2010，25(3):1883-1887．

［8］Clement K，Haesen E，Driesen J．The impact of charging plug-in hybrid electric vehicles on a residential distribution grid［J］．IEEE Transactions on Power Systems，2010，25(1):271-380．

(，cont．on p.56)(，cont．from p.32)

［9］罗卓伟，胡泽春，宋永华，等 (Luo Zhuowei，Hu Zechun，Song Yonghua，et al．)．电动汽车充电负荷计算方法 (Study on plug-in electric vehicles charging loading calculating)［J］．电力系统自动化 (Automation of Electric Power Systems)，2011，35(14):36-42．

［10］孙小慧，刘锴，左志 (Sun Xiaohui，Liu Kai，Zuo Zhi)．考虑时空间限制的电动汽车充电站布局模型 (A spatiotemporal location model for locating electric vehicle charging stations)［J］．地理科学进展 (Progress in Geography)，2012，31(6):686-692．

［11］葛少云，冯亮，刘洪，等 (Ge Shaoyun，Feng Liang，Liu Hong，et al．)．考虑电量分布及行驶里程的高速公路充电站规划 (Planning of charging stations on highway considering power distribution and driving mileage) ［J］．电力系统自动化设备 (Electric Power Automation E-quipment)，2013，33(7):111-116．

Coordinated planning of multi-type electric vehicle charging stations based on maximal entropy theory

WU Jian-sheng1，2，LI Xiao-zhou1

(1．Key Laboratory for Environmental and Urban Sciences，Shenzhen Graduate School，Peking University，Shenzhen 518055，China;2．Key Laboratory for Earth Surface Processes，Ministry of Education，College of Urban and Environmental Sciences，Peking University，Beijing 100871，China)

The paper presents a planning method of electric vehicle charging stations based on the maximal entropy theory．The distribution entropy of electric vehicle is firstly defined to describe the coincidence between the location of charging stations and charging load based on different characteristics of multi-type electric vehicle charging stations．Then the multi-type electric vehicle charging stations planning model is established based on a multi-objective method．And after defining the desirability function of each objective，the genetic algorithm is applied to seek the solution．Finally，the planning model is applied in a 25 node road network to testify the method presented in this paper and the results are compared with that of the method in which only investment income is considered as the objective．Results of the method in this paper show that the proportions of charging stations distribution are relatively close，which indicates better coincidence between the distribution of electric vehicle charging stations and charging load．

electric vehicle，charging station planning;charging mode;maximal entropy

TM715

A

1003-3076(2015)09-0029-04

2015-02-05

国家自然科学基金资助项目(41271101)

吴健生(1965-)，男，湖南籍，教授，博士，研究方向为城市规划、景观生态与GIS;

李小舟(1987-)，女，广西籍，硕士研究生，研究方向为城市规划、城市交通与碳排放。