数控滚齿机几何误差补偿技术研究

韩 江， 王国权， 夏 链， 田晓青， 吴 涛

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

齿轮是重要基础件，数控滚齿机作为主要的齿轮加工工作“母机”，其精度决定了齿轮的加工精度。影响数控滚齿机加工精度的误差元素主要有几何误差、力致误差和热致误差［1］，几何误差是机床原始制造误差引起的系统性误差，其在机床因素中所占比例较大，为20%～30%。因此，研究分析数控滚齿机的几何误差特性并对其进行补偿，对提高最终的齿轮精度具有十分重要的意义。

关于数控机床的误差补偿技术，国内外众多学者都作了相关的研究。文献［1－2］基于多自由度激光光学系统在线测量技术对机床的几何误差进行了补偿，利用机器人运动学原理，得到多轴数控机床的几何和热误差综合模型，并通过实时误差补偿提高了机床加工精度。文献［3］提出了基于3D探头检测五轴数控机床空间精度的方法，该方法既可以测量五轴机床移动轴的误差，又可以测量旋转轴的误差；文献［4］用齐次坐标变换原理推出了加工中心的几何和热误差综合模型，并且实现了补偿。

本文基于多体系统理论研究分析数控滚齿机的几何误差，得到了几何误差模型；并通过激光干涉仪的12线法［5］测量辨识出了滚齿机床移动轴的21项误差元素，通过球杆仪测量辨识出转动轴的12项误差元素；最后，将辨识出的结果代入误差模型得到各轴独立的误差补偿量并叠加到控制系统实施补偿。

1 几何误差模型的建立与解耦

建立准确的几何误差模型是机床误差辨识和补偿的基础。目前三角几何法、神经网格法和误差矩阵法等方法［6］能够用于几何误差模型的建立，但只有多体系统理论法综合考虑了复杂机械系统间的相互关系，并能够解决误差建模的准确性、通用性和自动化问题［7］。因此本文以多体系统理论［8］为基础来建立数控滚齿机几何误差模型。数控滚齿机物理结构简图如图1所示。

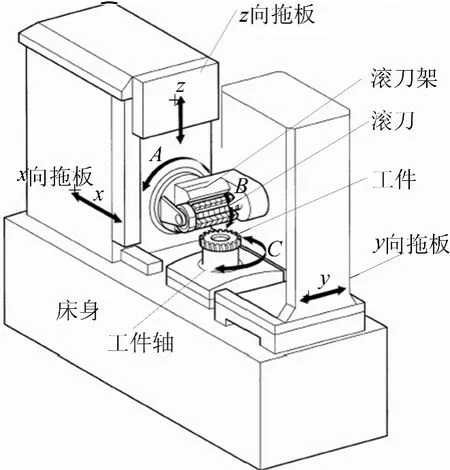
图1 数控滚齿机结构简图

依据多体系统理论建立的相邻体间的运动关系特征矩阵Tjk的表达式［9］为：

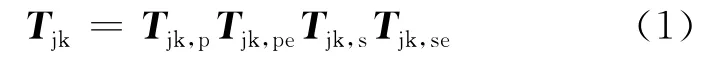
其中，Tjk，p为相邻体位置特征矩阵；Tjk，pe为相邻体位置误差特征矩阵；Tjk，s为相邻体位移特征矩阵；Tjk，se为相邻体位移误差特征矩阵。

对数控滚齿机各相邻体进行特征矩阵的求解，最终得到几何误差模型的表达式为：

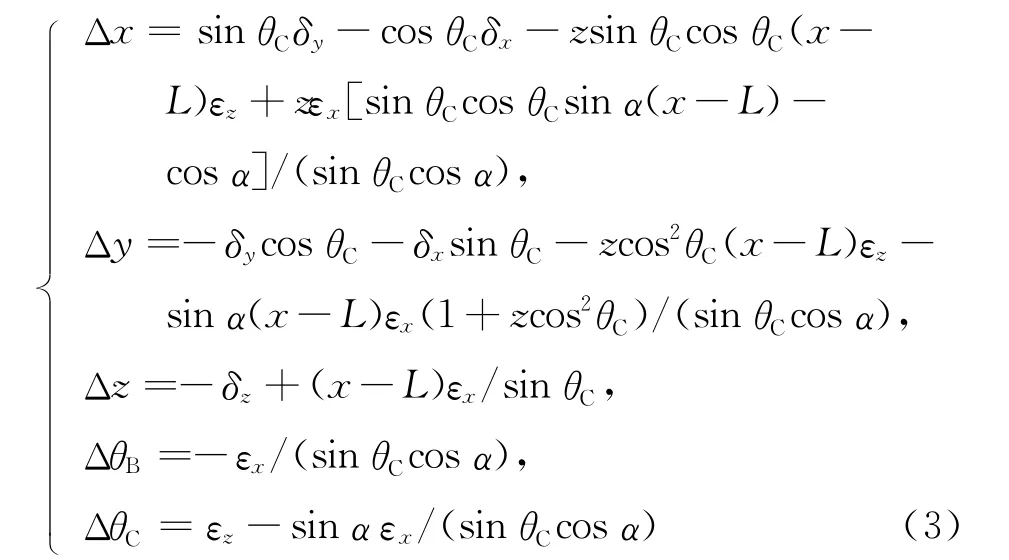
其中，δx、δy、δz分别表示刀具坐标系相对工件坐标系沿x、y、z轴的移动位移误差；εx、εy、εz分别为刀具坐标系相对工件坐标系绕x、y、z轴的旋转角度误差。

采用变微分法对得到的几何误差模型进行解耦［10］，得到机床各轴的误差补偿量为：

其中，α为加工斜齿轮时滚刀的安装角；θC为工件旋转角度；θB为滚刀的旋转角度；L为刀具坐标系相对工件坐标系在x方向的偏离距离。

2 几何误差元素辨识

2.1 移动轴几何误差辨识

数控滚齿机共有x、y、z轴3个移动轴。本文选择激光干涉仪的12线法对其进行测量辨识，12线法测量3个移动轴21项几何误差的测量示意图如图2所示，选取测量空间为135mm×45mm×410mm。

图2 12线法测量示意图

2.1.1 定位误差的辨识

数控滚齿机共有δx（xi）、δy（yi）及δz（zi）3个定位误差。用激光干涉仪分别测出图2中线1、2、3所示方向的位移误差，设测量起始点均为（0，0，0），终点分别为（xi，0，0）、（0，yi，0）和（0，0，zi）。位移误差即为定位误差，计算公式如下：

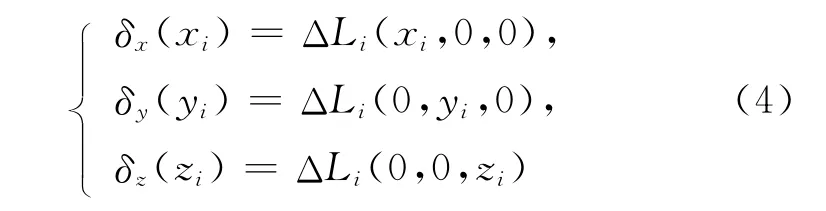
其中，ΔLi为理想与实际距离之差，即位移误差。

2.1.2 颠摆和偏摆误差的辨识

数控滚齿机颠摆和偏摆误差有：εx（yi）、εx（zi）、εy（xi）、εy（zi）、εz（xi）、εz（yi）。分别沿图2中线4～9每隔一定距离测量其位移误差值，并结合已获得的定位误差值，即可解得颠摆和偏摆误差，具体计算公式为：

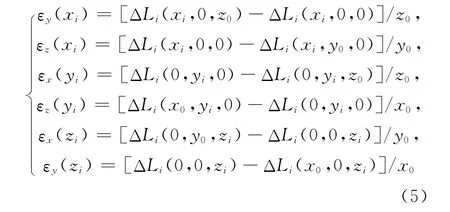
2.1.3 直线度误差的辨识

数控 滚 齿 机 共 有δy（xi）、δz（xi）、δx（yi）、δz（yi）、δx（zi）、δy（zi）6个直线度误差，直线度误差可以通过建立其与对应轴的偏摆和颠摆角度误差的关系获得，即

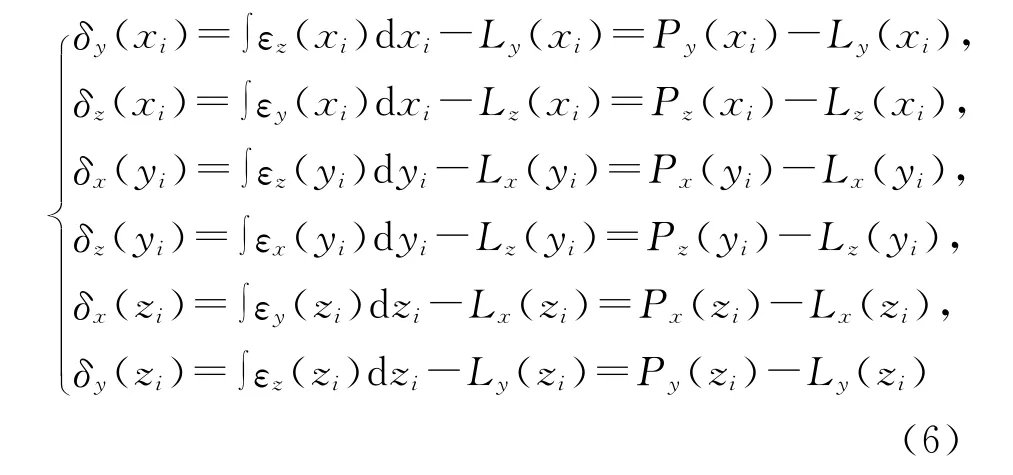
其中，Pu（vi）（u，v＝x，y，z且u≠v）为前i个测量点的偏摆误差或颠摆误差的积分，且这2种误差均可表示成测量点vi的n次多项式，n由拟合精度确定［11］。最佳拟合积分Pu（vi）的直线Lu（vi）的计算公式为：

基于最小二乘法拟合所得系数a、b的计算公式为：

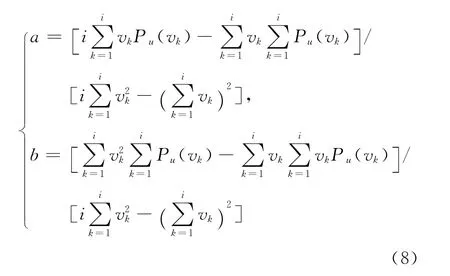
2.1.4 滚摆误差和垂直度误差的辨识

数控滚齿机共有εx（x）、εy（y）、εz（z）3个滚摆误差和Sxy、Syz、Sxz3个垂直度误差。分别沿图2中的线10～12每隔一定距离测量其位移误差值，构建数学模型，从中分离辨识出3个滚摆误差和垂直度误差如下：

2.2 旋转轴几何误差测量与辨识

数控滚齿机共有工件轴C和刀具轴B 2个旋转轴。由于数控滚齿机旋转轴的特定结构，其与五轴数控机床以及其他类数控机床旋转轴几何误差辨识方法有所不同，因此，本文以C轴为例，提出一种新的球杆仪分离辨识6项误差元素δx（θC）、δy（θC）、δz（θC）、εx（θC）、εy（θC）及εz（θC）的方法。刀具轴B辨识方法与C轴类似。球杆仪的测量安装示意图如图3所示。设初始状态P点的齐次坐标为［L0H

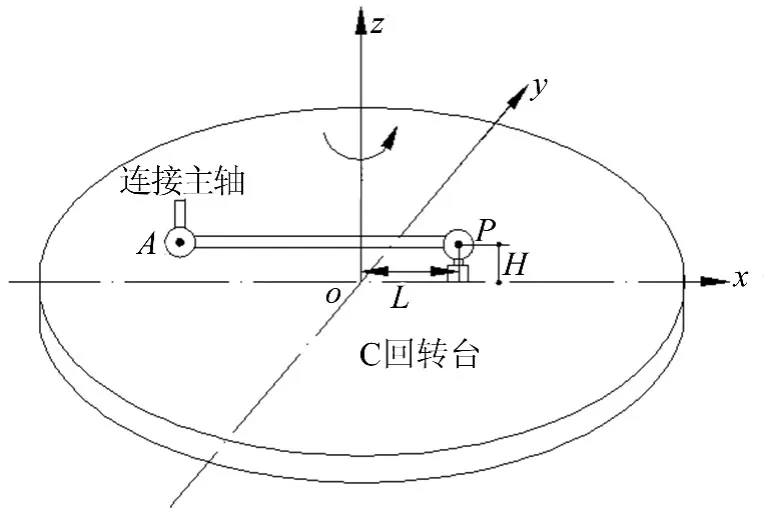
图3 C转台球杆仪测试安装示意图

1］T，C转台回转角度为αC，在理想状态下P点的坐标为：

实际情况下，当C转台作回转运动时会产生位移误 差δx（θC）、δy（θC）、δz（θC）和 转 角 误 差εx（θC）、εy（θC）、εz（θC），因此其误差变换矩阵为：

由于误差的存在，P点实际坐标为：

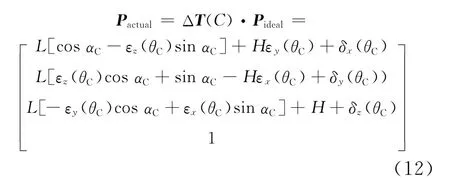
实际坐标与理论坐标之差为：

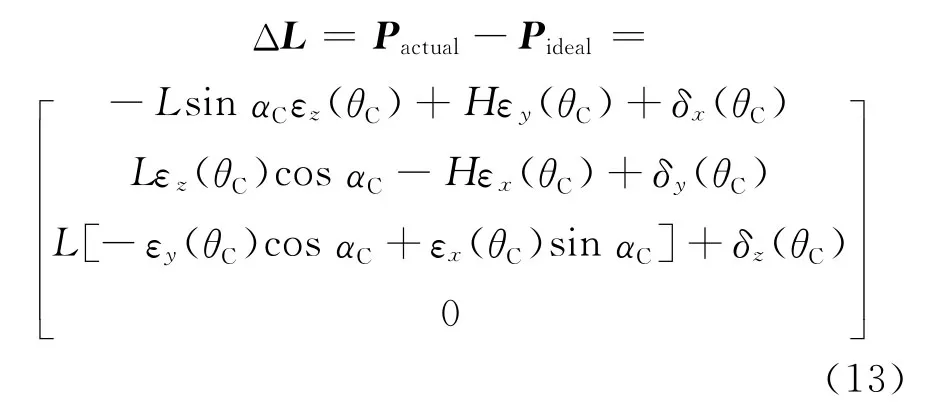
测量过程中，设A点的坐标为点的坐标为测量时保持理论杆长l0不变，则有：

测量中先选取一组测量组合L和H，当旋转角度为αi时，任取一个值y1，求得对应的z1，连续取3次，得到y1、z1，y2、z2，y3、z3。编制程序，控制主轴按上述3个位置运动，即可得到3个杆长变化量。测量过程如图4所示。

图4 球杆仪测量示意图

当球杆仪每处于1个位置时，记录球心A和P的坐标。假设轴3个方向的夹角为A、B、C，则测量中心座球心A在x＝x0平面3个不同的位置，可得：

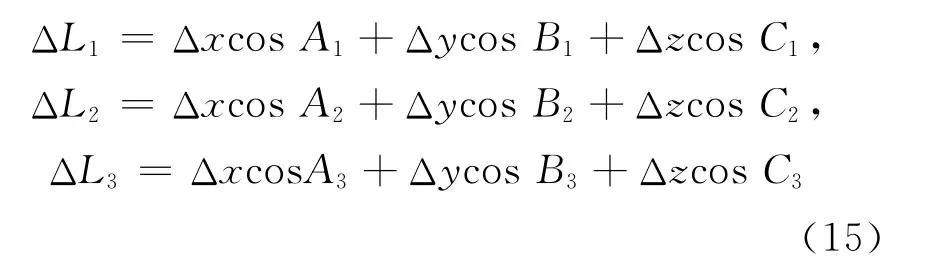
其中，ΔLi为球杆仪杆长变化量；Δx、Δy和Δz分别为x、y、z方向理想坐标与实际坐标之差。由（15）式可得出Δx、Δy和 Δz的值，即为（13）式矩阵中的值。通过3次改变L和H的不同组合值得到3种不同的测量模式，联立方程最终可以解出C转台所有的6项误差元素，公式如下：

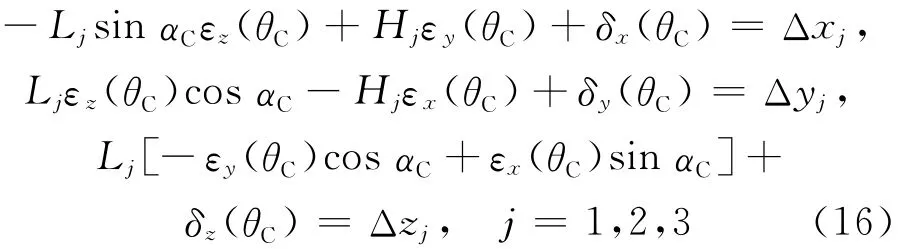
3 几何误差补偿

误差补偿实施是通过移动数控机床上的运动副以使刀具与工件在机床空间误差的逆方向上有一相对运动而实现的。目前主要有2种面向数控（computer numerical control，CNC）滚齿机型的补偿策略，即反馈中断法和原点平移法［12］。反馈中断法是将空间误差补偿信号插入伺服系统的反馈环中以实现补偿，不需要改变CNC控制软件，但需要特殊的电子装置。原点平移法是将空间误差量作为补偿信号送至CNC控制器，通过I／O口平移控制系统的参考原点以实现误差补偿，不影响执行的工件程序，但要修改CNC控制器中的PLC程序。

数控机床几何误差补偿的有效实施不仅取决于准确的误差模型和合适的辨识方法，还要有适应所开发系统的补偿机制。针对数控滚齿机，本课题组基于ARM＋DSP＋FPGA嵌入式平台，开发了拥有完全自主知识产权的滚齿数控系统，ARM内嵌Windows CE操作系统主要完成丰富的人机交互功能。其中，ARM为RISC微处理器；DSP为数字信号处理器；FPGA为现场可编程门阵列。

DSP主要完成系统的复杂运算和实时控制功能，如插补、位控等。ARM和DSP之间通过HPI（host port interface）高速并行总线交换数据，实现前后台通信的协调。FPGA网络主机是一座“数据桥梁”，负责上层CPU与下层网络键盘板、网络I／O接口板等从机节点之间包括运动控制命令、键盘指示灯信息在内的数据交换。本文提出以下几何误差补偿策略。

首先通过激光干涉仪和球杆仪在离线情况下测得与误差参数相关的几何误差元素，再通过专门的输入输出接口将运动位置信号送入PC机。在PC机内，将测得的误差值经参数辨识后传入几何误差元素数据库，给各误差元素赋值，再根据事先建立的综合数学模型计算刀具相对工件的误差，然后对误差模型进行解耦和离散化处理得到各轴独立的误差补偿量，送至CNC控制器输入模块实施补偿。数控滚齿机几何误差补偿策略如图5所示。

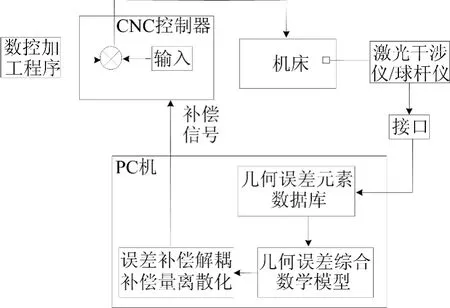
图5 数控滚齿机几何误差补偿策略

在本系统中，由于DSP要完成复杂的运算和实时控制，为了避免给DSP增加负担，在ARM平台上进行几何误差补偿软件的开发，并利用ARM在界面开发上的优势对误差补偿过程进行控制，如观察补偿状况等。在ARM内部，考虑到补偿的方便性和简洁性，在其中的编译环节实施补偿。补偿界面如图6所示。

图6 误差补偿界面

在具体的误差补偿过程中，考虑到机床响应的速度以及运行的精度和平稳性，对各运动轴取一系列离散点进行补偿，然后将实测的误差补偿点列成误差修正表存入计算机，当机床的的实际变量与误差修正表中的某一数据点相同时，通过查表取出该点的误差修正量，进行误差修正。

4 结束语

本文在建立的数控滚齿机几何误差模型的基础上，基于激光干涉仪的12线法辨识出了移动轴的21项误差元素，并通过球杆仪将回转轴的12项误差元素辨识出来。这种辨识方法与其他方法相比，具有测量更简单、限制条件更少以及测量设备少等特点。最后基于本课题组所开发的数控滚齿系统，提出了适合本系统的几何误差补偿策略。随着高性能高精度数控机床的不断发展，本文辨识和补偿技术对齿轮加工精度的提高具有一定的理论与实际意义。

［1］韩 江，姜小飞，夏 链，等.数控滚齿机刀架温度场及热误差仿真分析［J］.合肥工业大学学报：自然科学版，2013，36（11）：1285－1288，1387.

［2］Ni Jun.CNC machine accuracy enhancement through realtime error compensation［J］.Journal of Manufacturing Science and Engineering，1997，119（4B）：717－725.

［3］Lei W T，Hsu Y Y.Error measurement of five－axis CNC machines with 3Dprobe－ball［J］.Journal of Materials Processing Technology，2003，139（1／2／3）：127－133.

［4］杨建国，许黎明，刘 行，等.加工中心的几何误差和热误差综合补偿模型［J］.计量学报，2001，22（2）：90－94.

［5］张舒杰.数控机床运动误差分步辨识法理论与实验研究［D］.上海：上海交通大学，2010.

［6］Srivastava A K，Veldhuis S C，Elbestawit M A.Modeling geometric and thermal errors in a five－axis CNC machine tool［J］.International Journal of Machine Tools ＆ Manufacture，1995，35（9）：1321－1339.

［7］粟时平，李圣怡，王贵林.基于空间误差模型的加工中心几何误 差 辨 识 方 法 ［J］.机 械 工 程 学 报，2002，38（7）：121－125.

［8］刘又午.多体动力学的休斯敦方法及其发展［J］.中国机械工程，2000，11（6）：601－607.

［9］曲智勇，陈维山，姚 郁.某型六自由度运动系统误差建模［J］.哈尔滨工业大学学报，2007，39（9）：1345－1349.

［10］要小鹏，殷国富，方 辉，等.五轴数控机床的空间误差建模与 解 耦 补 偿 分 析 ［J］.高 技 术 通 讯，2011，21（10）：1084－1089.

［11］刘建军.多轴数控机床几何误差辨识与补偿技术研究［D］.成都：西南交通大学，2012.

［12］李永祥.数控机床热误差建模新方法及其应用研究［D］.上海：上海交通大学，2007.