宽带跳频通信系统频域均衡算法
李 勇,姚富强,关胜勇,许 拔
(1.解放军理工大学通信工程学院,江苏南京210007; 2.总参第63研究所,江苏南京210007)
宽带跳频通信系统频域均衡算法
李 勇1,2,姚富强2,关胜勇2,许 拔2
(1.解放军理工大学通信工程学院,江苏南京210007; 2.总参第63研究所,江苏南京210007)
针对差分跳频通信系统跳频带宽宽、瞬时带宽窄的信号特点,提出了一种差分跳频均衡算法——基于最小均方算法的多跳联合频域均衡算法。分析了最小均方误差准则频域均衡与单符号最小均方频域均衡对宽带差分跳频通信系统的不适用性,从而提出适用于差分跳频通信系统的多跳联合最小均方频域均衡算法,给出了算法详细的设计过程和结构。对算法性能在频率选择性衰落信道条件下进行仿真评估,结果表明本算法对差分跳频通信系统的信道均衡性能具有显著的作用,能提高差分跳频系统的解调误码性能。
频域均衡;差分跳频;码间干扰;最小均方
0 引 言
差分跳频通信系统[12]是一种新型的跳频通信方式。它具有跳频带宽宽、跳频速率高等特点。差分跳频技术通常应用于短波跳频通信,信号利用电离层的反射在短波天波信道中传输。短波信道通常存在多径衰落。从时域来看,如果信道的冲激响应扩散到多个符号就会发生严重的符号间干扰(inter-symbol interference,ISI),从而导致信号失真;从频域来看,如果传输信号的带宽超过了信道的相干带宽(多径时延的倒数)就会引起频率选择性衰落,导致传输信号的各个频率分量经历不同的衰落,称这种信道为频率选择性衰落信道。通常,短波信道的多径时延大约在零点几毫秒到几毫秒之间,其相干带宽为几百赫兹到几千赫兹。差分跳频的跳频带宽达到1.28 M Hz,远远超过信道相关带宽,会受到频率选择性衰落,导致系统的性能下降。采用信道均衡技术是改善差分跳频系统性能的有效方法。
信道均衡可在时域实现(称为时域均衡器(time domain equalization,TDE)),也可在频域实现(称为频域均衡器(frequency domain equalization,FDE))。TDE的复杂度随着信道的记忆性呈指数增加。而采用高效的快速傅里叶变换(fastFourier transform,FFT)的FDE相对于TDE来说有更低的计算复杂度。
近20年来,在采用分块传输和单载波(single carrier, SC)调制机制的宽带无线通信系统中提出了低复杂度的频域均衡技术,并得到广泛应用。文献[3]提出了在单载波宽带无线通信系统中采用频域均衡技术,获得比OFDM更好的性能,在文献[4]中提出了Turbo迭代频域均衡,进一步提高系统性能。文献[5]在频率选择性衰落信道中采用单载波频域均衡技术,使空时分组编码传输技术在低复杂度的情况下获得了较大的分集增益。文献[6]提出了线性频域均衡技术在宽带航空遥测信道中的有效应用。文献[7-10]提出了多种适用于单载波传输技术的频域均衡算法,使频域均衡算法的复杂度和性能得到进一步提高。频域均衡技术对单载波系统的性能提升的文献相对较多,但对于宽带差分跳频通信系统的研究还未见报道。本文旨在采用频域均衡技术提高差分跳频系统的误码性能。
差分跳频通信系统利用相邻跳信号频率之间相互关系携带信息。在每一跳信号驻留时间内,差分跳频信号是一个无调制的单音信号,从频谱上来看只有一根谱线。接收机通过信号处理获得接收信号的频谱特征,根据频谱特征完成系统同步并检测出当前跳信号的频率,结合前一跳信号的频率,根据两跳信号频率间的相互关系译出信息。接收机在频域完成信号频率的判决,因此在频域对差分跳频系统进行非常便利。
本文提出了一种适应于宽带差分跳频通信系统的多跳联合最小均方频域均衡(M H-LMS-FDE)算法。频域均衡技术在常规通信系统中得到广泛应用,但在跳频通信系统中的应用还未见相关文献。本文旨在采用频域均衡技术提高差分跳频通信系统的性能。
1 信道及信号模型
差分跳频系统的系统框图如图1所示。

图1 差分跳频系统框图
首先,差分跳频系统将跳频带宽内的频率资源分为N个频率,形成跳频频率集f{f0,f1,…,fN-1}。通信时,每跳驻留时间内的信号是从这个频率集中选出的一个频率,假设Fn为当前跳信号的频率,Fn-1为前一跳信号的频率,则Fn=fi(0≤i<N)。二进制数据流经过串并变换形成式中,Ts为跳频驻留时间;Es是跳频信号的能量;Fi是发送信号在第i跳驻留时间内的频率;Fc为系统的中心频率; g(t)是在跳频驻留时间内幅度为1的矩形脉冲。通过信道后的接收信号为信道冲激响应与发送信号s(t)的卷积,即 m bits的数据符号xn。xn和前一跳信号的频率Fn-1送入频率转移函数进行编码,生成当前跳信号的频率Fn。此编码过程可表示为

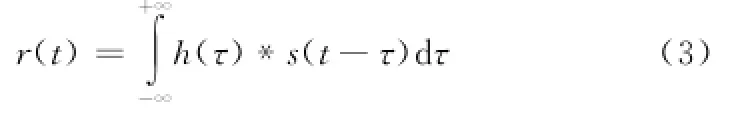

式中,G为频率转移函数,它对差分跳频通信系统的误码率性能起着重要的影响。
当前跳信号的频率Fn控制频率合成器,产生在信道中传输的当前跳信号s(t)。由于每一跳携带m bits信息,从前一跳信号频率转移到当前跳信号频率有2m个可能的频率,这2m个频率组成的集合是跳频频率集f的一个子集。发送信号可表示为
式中,h(τ)信道冲激脉冲响应。
用频率为N/Ts的采样时钟对接收信号进行采样,那么每一跳驻留时间内可得到N个离散信号采样点。采样后的离散信号经过数字下变频变为基带信号,其离散等效低通信号为

式中,hl(k)为信道冲激响应的离散等效低通形式;sl(k)为发送信号的离散等效低通形式。
从式(2)可得sl(k)为

式中,ωn=2πFn/N;N为一跳驻留时间内信号的采样点数。
对式(5)进行离散傅里叶变换,可得

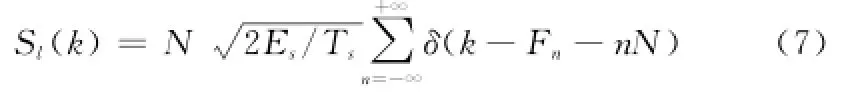
接收信号在时域可表示为信道冲激响应与发送信号的卷积,在频域可表示为乘积形式
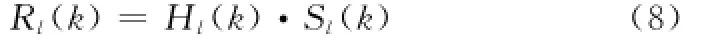
式中,Hl(k)为信道冲激脉冲响应的离散傅里叶变换。
为了表示简洁,省略表示等效低通的下标l,并用上标(n)表示第n跳信号,并且考虑在信号中加入加性高斯白噪声。在第n跳驻留时间内,频域均衡器的输入信号的矩阵形式为

由于ωn=2πFn/N,ω=2π/N,式(6)可化简为跳信号的离散时间采样序列;H(n)≜diag(DFTN[h(n)]),是信道离散时间采样的冲激响应;V(n)是零均值相互独立的加性高斯白噪声矢量的频域形式;DFTN[x]表示矢量x的N点离散傅里叶变换;diag(x)表示以矢量x的元素做主对角线上的元素的对角阵。
经过频域均衡后,均衡器的输出矩阵形式为

式中,w(n)是均衡器的频域滤波器系数矢量。
2 频域均衡算法
与时域均衡器相似,频域均衡器的设计准则包括:峰值失真准则、最小均方误差准则和自适应准则等。本文提出的是基于MMSE准则的M H-LMS-FDE算法。
2.1 MMSE频域均衡(MMSE-FDE)及LMS频域均衡
(LMS-FDE)算法
MMSE准则的目标是使系统输出与输入信号误差的均方值最小。MMSE-FDE可以由线性滤波器实现。均衡器的输入信号与输出之间的误差为δ,则由式(9)和式(10)可得

均方误差为

式中,(·)H表示矩阵的厄密共轭。
将式(11)代入(12),则均方误差可表示为(为了表示简单,省略上标)

使式(13)最小,等价于令Δ对w的偏导数为0,即

对于常规的系统,如发射信号各符号是等幅且相互独立,并与噪声不相关,经归一化后,则式(14)可化简为

如果能准确知道信道的增益矩阵H及信道中的噪声功率等信息,且HHH+σ2I是可逆的,可由式(15)求得频域均衡滤波器的最佳滤波系数为

式(16)为采用M MSE准则时的频域均衡器的最优算法。不幸的是,通常情况下信道的增益矩阵H与噪声功率不能预知,因此采用基于最陡下降算法的最小均方算法(least-mean-square,LMS)求解,构成最小均方频域均衡器(least-mean-square-frequency domain equalization,LMS-FDE)。其基本思想是通过递推计算滤波器的滤波系数,即第k+1时刻的系数由第k时刻的系数通过下式来计算式中,上标(k)表示第k个符号时刻;μ是调整步长因子; E(k)是第k个符号时刻均衡器输出信号与系统期望响应之间误差的频域表示。E(k)定义为


式中,Z(k)为如式(10)所定义的第k个符号时刻均衡器的输出;D(k)为第k个符号时刻系统期望响应。
通过式(17),就可以完成对常规系统进行频域均衡。对于常规系统,在每一个符号时间间隔内,其频谱占用了所有的发射带宽,信号的频率响应能完全反映信道的频率响应。由式(7)可知,差分跳频通信系统在每一跳驻留时间内是一单音窄带信号,带宽只占系统跳频带宽的1/N。因此,一跳驻留时间内的差分跳频信号只能反应信道在特定频率处的信道频率响应而不能充分反映信道频率响应全貌,采用式(17)的公式对差分跳频信号进行频域均衡存在问题,需要一种改进的方法进行。
2.2 多跳联合最小均方频域均衡(MH-LMS-FDE)
在一跳驻留时间内对差分跳频系统进行频域均衡只能单独对一个子信道(大约占系统跳频带宽的1/N)进行均衡,而不能对整个跳频带宽进行联合均衡。差分跳频系统的信息解调不是在一跳内完成,而是由相邻两跳信号的频率相关性完成信息解调,这就需要在整个跳频带宽内进行均衡。显然,式(17)所示的频域均衡器并不适用于对差分跳频通信系统均衡。
由式(7)可知,差分跳频信号在每一跳驻留时间内的是一单音窄带信号。但是在整个时间轴上,差分跳频信号遍历系统的跳频带宽,即在连续多个跳频驻留时间内观察差分跳频信号,其频谱可能完全占用了系统的跳频带宽,该频谱响应可以比较充分反映信道的频率响应。因此,把多跳信号联合起来对差分跳频信号进行频域均衡是一种行之有效的方法。
把跳频信号序列分块,每Ns个连续跳频信号为一个分块,用下标(k)表示第k个跳频信号分块,用上标(i)表示跳频分块中的第i个跳频信号,则系统的期望响应可以用一个N×Ns的矩阵D(k)表示

式中,D((ik))表示第k个跳频信号分块内第i个跳频信号的频域期望响应;d((ik))是相应的时域波形采样矢量。
相应地,均衡器输出信号也按每Ns个连续跳频信号分为一块,均衡器输出信号向量矩阵可表示为

定义E(k)为均衡器输出信号与系统期望响应的误差矩阵,则E(k)可表示为

对误差矢量矩阵E(k)的列矢量进行平均,求得平均误差矢量

同样,对接收信号矩阵R(k)的列矢量进行平均,求得平均接收信号矢量

用式(22)中的¯E(k)和式(23)中的¯R(k)分别代替式(17)中的E(k)和R(k),可得到差分跳频通信系统的MH-LMSFDE的频域滤波器的滤波系数的递推关系
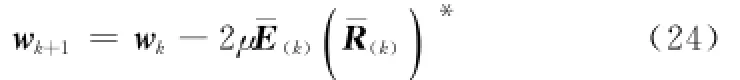
由式(24)定义的适用于差分跳频通信系统的M HLMS-FDE系统框图如图2所示。
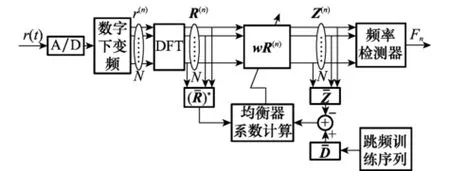
图2 基于MH-LMS-FDE的差分跳频系统框图
2.3 算法参数选择及训练序列设计
在本算法中,有两个参数需要精心设计,一个是调整步长因子μ,另一个是跳频信号分块长度Ns。调整步长因子μ对算法的收敛过程有很大的影响,μ必须满足收敛条件。并且,在收敛范围内,μ越大,收敛速度越快,但μ越大,过渡过程将出现振荡。Ns的大小决定了收敛性及稳态误差,如果Ns值过小,由于一个符号分块矩阵内响应不能充分反应信道响应,可能不满足算法的收敛条件,即使能满足收敛条件,稳态误差也可能得不到保障;如果Ns值过大,算法的收敛速度将受到影响,但其稳态误差得以保障。μ值的选择在文献[11]中已有详尽的阐述,在此不再赘述。本文只考虑Ns值的设计选择。
根据差分跳频通信系统的信号特征,系统的期望响应D(k)具有如下形式

式中,A(Fi,i)表示在第Fi行第i列有幅度为A(A为跳频信号的幅度)的元素;Fi是该第i跳信号的频率号。要使D(k)能充分反映信道响应,在Ns个跳频驻留时间内,跳频信号的频率应遍历跳频带宽内的N个频率。由式(25)可知,要满足这个条件,只需矩阵D(k)的秩不小于N。即

式中,D(k)是一个N×Ns阶矩阵,rank(D(k))≤min(N,Ns),要使式(26)成立,则必须满足关系式Ns≥N。考虑到算法的收敛速度,Ns应尽可能小。因此,符号分块长度参数Ns取最小值N。
当分块长度参数取值定为N后,矩阵D(k)变为一个N×N阶方阵。由于D(k)的每一列向量只有一个非零元素,最简单的秩为N的N×N阶方阵是单位阵IN×N。通过训练序列的精心设计,可以获得分块长度为N的训练序列,其矩阵形式为对角矩阵A·IN×N,其中A为跳频信号的幅度。此矩阵形式的期望响应具有明显的特征,即从跳频驻留时间间隔1到时间间隔N,频率号递增。此特征与信息序列的特征差别太大,隐蔽性差。因此,对对角矩阵A· IN×N进行多次初等变换,得到如式(25)的N×N阶系统期望响应方阵。
3 仿真结果分析
考虑一个频率选择性衰落信道,其时域滤波器系数为c(1)=1,c(2)=0,c(3)=0.3exp(0.7j),c(4)=0,c(5)=0, c(6)=0.2exp(-0.8j)。这是一个频率响应起伏比大的频率选择性衰落信道,其频率响应如图3所示。

图3 信道频率响应
首先对算法的收敛速度和稳态误差进行仿真分析。假设差分跳频通信系统的跳频频率数N=64,系统除受信道衰落影响外还受加性高斯白噪声的影响,仿真结果如图4和图5所示。图4是在不同信噪比情况下,均方误差与迭代次数的关系曲线;跳频信号分块长度Ns=N,调整步长因子μ=0.007。从图4可以看出,在较小信噪比情况下,本算法也能工作;在不同的信噪比情况下,算法的收敛性基本相同,但随着信噪比的提高,均衡后的均方误差不断减小。图5是在跳频信号分块长度不同的情况下,均方误差与迭代次数的关系曲线;信噪比固定为27 dB,调整步长因子μ=0.007。从图5可以看出随着跳频信号分块长度的增加,其均方误差性能有所提高;但由于图中一次迭代是按跳频信号分块长度Ns个跳频驻留时间进行的,因此其收敛速度可以看成是与跳频信号分块长度Ns成正比的。

图4 不同SNR情况下均方误差与迭代次数关系

图5 不同分块长度情况下均方误差与迭代次数关系
图6是在信噪比为7 d B时的均衡算法性能仿真曲线。调整步长因子μ=0.007,跳频信号分块长度Ns=128。图6(a)为迭代次数与均方误差关系曲线;图6(b)为信道的频率响应;图6(c)为均衡器进入稳定状态时的频率响应;图6(d)为信道与均衡器的共同频率响应。由图可以看出,在信噪比为7 dB时,均衡算法能正常工作;经过均衡后,在各个频率处的衰减基本相同,克服了频率选择性衰落的影响。

图6 信噪比为7 dB时的均衡算法性能仿真曲线
图7是在信噪比为17 dB时,在不同的迭代次数后均衡器与信道的共同频率响应。从图中看出,随着迭代次数的增加,均衡器与信道的共同频率响应趋于平稳,均衡器输出的在各个频率的衰落越趋于相等,最终达到稳态,表明均衡算法适应于DFH系统。

图7 信噪比17 dB时不同迭代次数后均衡器与信道的共同频率响应
图8是差分跳频系统采用本文提出的算法进行均衡与不进行均衡情况下系统的误码率性能比较。从图8可以看出,采用MH-LMS-FDE算法的系统性能比原系统性能有显明的改善,随着信噪比的提高,其性能改善也越大,且随着分块长度的增加,系统获得的增益也越大。从图4和图5得出的结论(在大信噪比及分块长度大的情况下均衡后的稳态误差比在小信噪比及分块长度小的情况下均衡后的稳态误差小)在此也得到了验证。
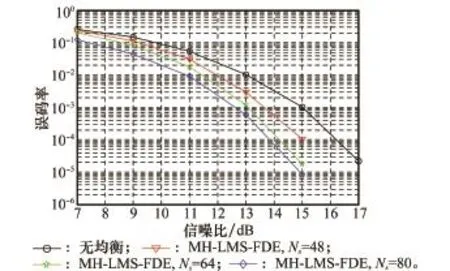
图8 系统误码率性能比较
4 结 论
本文分析了差分跳频系统的信号特点,找出了将MMSE频域均衡器与LMS频域均衡器应用于差分跳频通信系统时存在的问题,提出了适用于差分跳频通信系统的多跳联合最小均方频域均衡算法,并对算法进行仿真评估,结果表明本算法有很好的收敛性和较小的均方误差,对宽带差分跳频通信系统有很好的适应性。
[1]Herrick D L,Lee P K.CHESS:A new reliable high speed HF radio[C]∥Proc.of the IEEE Military Communications Conference,1996:684-690.
[2]Mills D G,Edelson G S,Egnor D E.A multiple access differen-tial frequency hopping system[C]∥Proc.of the IEEE Military Communications Conference,2003:1184-1189.
[3]Falconer D,Ariyavisitakul S L,Benyamin-Seeyar A,et al.Frequency domain equalization for single-carrier broadband wireless systems[J].IEEE Trans.on Communication Magzine,2002,40(4):58 -66.
[4]Benjamin N G,Chan-Tong L,Facloner D.Turbo frequency domain equalization for single-carrier broadband wireless systems[J]. IEEE Trans.on Wireless Communication,2007,6(2):759-767.
[5]Al-Dhahir N.Single-carrier frequency domain equalization for space-time block-code transmission over frequency-selective fading channels[J].Trans.on IEEE Trans.on Communication Lettter,2001,5(7):1029-1033.
[6]Williams I E,Saquib M.Linear frequency domain equalization of SOQPSK-TG for wideband aeronautical telemetry channels[J]. IEEE Trans.on Aerospace and Electronic Systems,2013,49 (1):640-647.
[7]Zhang X H,Chen E Q,Mu X M.Single-carrier frequency-domain equalization based on frequency-domain oversampling[J]. IEEE Communication Lettter,2012,16(1):24 26.
[8]Bai N,Li G F.Adaptive frequency-domain equalization for mode-division multiplexed transmission[J].IEEE Photonics Technology Letters,2012,24(21):1918-1921.
[9]Rashobh R S,Khong A W H.A fast frequency-domain algorithm for equalizing acoustic impulse responses[J].IEEE Signal Processing Letters,2012,19(12):797-800.
[10]Wang X Y,Wang Z Y,Gao X C,et al.Variational inferencebased Turbo frequency domain equalization and channel estimation[J].Systems Engineering and Electronics,2013,35(2): 425-429.(王行业,王忠勇,高向川,等.基于变分推理的Turbo频域均衡与信道估计[J].系统工程与电子技术,2013,35(2): 425-429.)
[11]Proakis J G.Digital communications[M].5th ed.McGraw-Hill Companies,2007.
Frequency domain equalization for broadband FH system
LI Yong1,2,YAO Fu-qiang2,GUAN Sheng-yong2,XU Ba2
(1.Institute of Communications Engineering,PLA University of Science and Technology,Nanjing 210007,China; 2.The 63rd Research Institute of the PLA General Staf f Headquarters,Nanjing 210007,China)
The signal of the differential frequency hopping system has a broadband when it hops,and has a narrowband in each hop.This paper proposes a frequency domain equalization algorithm for the differential frequency hopping system,i.e.,the multi-hopping frequency domain equalization algorithm based on the leastmean-square.The shortages of the frequency domain equalization algorithm based on minimum mean square error criteria and the least-mean-square frequency domain equalization algorithm are analyzed,and then the multihopping frequency domain equalization algorithm is proposed based on the least-mean-square for the differential frequency hopping system.The algorithm design and its structure are given in detail.The simulation result shows that the proposed algorithm is very efficient to equalize the channel for the differential frequency hopping system over a frequency-selective fading channel,and can improve the BER performance of the frequency hopping system.
frequency domain equalization(FDE);differential frequency hopping(DFH);inter-symbol interference(ISI);least-mean-square(LMS)
TN 92
A
10.3969/j.issn.1001-506X.2015.03.28
李 勇(1977-),男,工程师,博士研究生,主要研究方向为军事通信抗干扰与无线通信。
E-mail:Liy771121@163.com
姚富强(1957-),男,研究员,博士,主要研究方向为军事通信抗干扰与无线通信。
E-mail:yaofuqang57@163.com
关胜勇(1967-),男,高级工程师,博士,主要研究方向为军事通信抗干扰与无线通信。
E-mail:469346770@qq.com
许 拔(1981),男,工程师,博士,主要研究方向为军事通信抗干扰与无线通信。
E-mail:906677370@qq.com
网址:www.sys-ele.com
1001-506X(2015)03-0652-06
2014 05 14;
2014 09 01;网络优先出版日期:2014 10 21。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141021.1102.003.html
国家自然科学基金(61102091);解放军理工大学2013年预先研究青年基金项目(KY63ZLXY1301)资助课题

