基于阶段划分的股市信息冲击的非对称性分析

周 宇

(湖南省物流职业技术学院， 湖南 长沙 410000)



基于阶段划分的股市信息冲击的非对称性分析

周 宇

(湖南省物流职业技术学院， 湖南 长沙 410000)

基于AR-EGARCH-M模型，对1991-2013年上证指数收益率序列的信息冲击非对称性进行分析.首先以年为单位分析了信息冲击的非对称性特征，根据非对称性效应的表现将其划分为6个阶段进一步分析.分析结果显示：A股市场表现出信息不对称性，信息冲击的正负杠杆效应交替出现，但是随着时间的推移，这种不对称性在明显减小.这表明中国股票市场的投机成分不断减少、投资者不断趋于理性，市场有效性水平提高.

投资管理；上证指数；非对称性;AR-EGARCH-M；信息冲击

1 引 言

很多金融资产(如股票、股指期货等)的波动率对价格下跌的反应明显要高于价格上升的反应，即其在信息冲击下表现出明显的非对称性.对此，学者们给出的解释是：因为较低的股价减少了股东权益，而股价的大幅下降扩大了公司的杠杆作用，进而提高了持有股票的风险，所以也被称为“杠杆效应”.这种非对称性效应在欧美股市与中国股市等已经得到了验证.但对不同时期的分析发现，得出的非对称性效应结果差异很大.经过20多年的发展，中国股市有效性水平得到了很大的提高，在股市发展的同时，其收益波动的非对称性特征有什么变化呢？收集了1991年以来上证指数的收盘价，运用AR-EGARCH-M模型对上证指数的收益波动的非对称性发展情况进行分析.

Engle[1]于1982年提出ARCH模型，ARCH模型能够较好的拟合金融时间序列中的时变方差与尖峰厚尾分布，得到了广泛应用.ARCH(q)模型虽然可以拟合金融时间序列中的异方差，但同时也存在缺点，即要对异方差实现较好的拟合效果必须取很大的滞后除数q，为了处理这个问题，1986年Bollerslev提出GARCH模型，该模型被用来描述信息冲击的对称的时间序列，并且可以大大降低被估计参数的个数.

许多学者使用GARCH模型研究股票市场价格指数等金融时间序列，但在研究的过程中发现，GARCH模型拟合的条件异方差是一个对称函数，与序列的波动幅度有关但并不能反映股票市场的非对称效应．一般观察研究认为，股票市场的股价在同时上涨一个百分点或者下降一个百分点时间内，股价下跌过程中的波动性更大.这种非对称性使得GARCH模型的研究结果可靠性不够.Christie(1982)的研究结论为，当股票价格下降时，资本结构中附加在债务上的权重会增加，若债务权重的增加的消息泄露后，资产持有者与购买者就有所预期——未来资产收益将导致更强的波动性，该股票价格波动将加大.为了能解释这种现象，从而较好地反映股票市场的这种变动特征，须对标准的GARCH模型进行进一步的修正.Nelson[2]于1991年提出了非线性的指数(Exponential)GARCH模型(EGARCH模型)，该模型能较好地克服标准GARCH模型的上述不足，同时也能较好地描绘出股市消息效应的非对称性.

股市存在诸多特征与效应，如，徐林等[3](2014)对上证指数对数收益率的长相依性进行了统计检验并完成了相应的统计建模以及参数估计，研究表明长相依性质对于股指风险有很大的影响.王璐[4](2013)利用马尔科夫体制转换ARMA(1,1)研究股市与债市的转换，发现股市和债市体制转换非对称，正相关状态持续期更长，体制转换中存在交替的逃离效应和传染效应特征.

对股市的非对称性研究文献主要集中于验证股票指数是否存在非对称性.模型选用方面，任彪，李双成[5]利用三种GARCH-M模型实证分析了中国股票市场不同发展阶段波动的非对称性特征，发现该模型是描述中国股市波动非对称性特征的最优模型.何帮强，惠军[6]以2000年1月11日-2006年3月15日上证综指和深证成指收盘价为样本，对中国沪深股市收益率分布用ARMA-EGARCH-M模型进行拟合，认为该模型能更有效地拟合中国沪深股市的波动性.陈潇，杨恩[7]研究了中美股市波动溢出效应和杠杆效应，发现沪市和深市都存在着显著的杠杆效应，与美国股市相比沪市和深市的杠杆效应较弱；沪市和深市之间存在着显著的双向波动溢出效应，沪市对深市的波动溢出效应更显著；美国股市与中国股市之间并不存在显著的波动溢出效应.杜莉萍[8]运用混合的ANN-EGARCH模型对沪深300指数进行实证分析，该结果证明此模型可以更有效的预测指数的短期波动趋势.

然而，股票市场不同阶段的非对称性特征存在很大差别，往往需要分阶段分析，陈浪南，黄杰鲲[9]划分了波动时段，并对各时段分别用GJRGARCH-M模型考察利好消息与利空消息对中国股票市场的波动性的非对称影响.韩贵，王静[10]利用1991-2007年中国上证综合指数的历史数据，根据股票市场大的波动周期分五阶段经过EGARCH(1，1)模型估计，以验证市场对信息冲出的反映情况.杨永，朱东洋[11]选取了2006年1月4日到2008年12月31日期间上证综合价格指数日收益率和收益波动率的数据资料，对中国牛熊市轮替过程中股票市场波动的非对称性分析，发现股票市场的波动在股改后牛熊市期间表现出显著的非对称性、杠杆效应和长记忆性.这些文献在阶段划分上具有一定的主观性，而且注重陈述事实，没有注意股市在发展过程中的成长与完善.

以上文献对股市波动的非对称性特征进行了深入研究，但仍存在不足：大部分对股市的非对称性特征研究不够全面，未划分阶段，而实际上不同阶段股市表现出的非对称性特征差异很大.与那些划分阶段的文献在方法上有所不同，首先运用AR-EGARCH-M模型对上证指数收益率序列波动对每一年的非对称性特征进行分析，在此基础上再对股市划分为6个阶段来研究其非对称性特征，从蔡晓春等[12]的研究得到启发，注重股市的的整体情况与发展趋势.

2 模型及数据

2．1 相关模型方法

股票收益序列因其自身惯性和滞后效应的影响，通常会呈现出不同程度的序列相关性.针对股票收益率序列的自相关性、有偏性、异方差性和尖峰厚尾等特性，另外，收益与风险成正比，因此，将波动项引入均值方程可以描述金融资产中包含风险的回报.若先建立收益率序列AR模型，然后再使用EGARCH-M模型处理异方差问题，这样就能够很好地解决股票收益序列存在这些特性，取得较理想的拟合效果.

在标准化的GARCH(1,1)模型中：

yt=xtγ+εt，

(1)

(2)

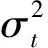
1)均值ω.

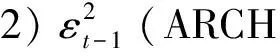
由于股票收益率序列可能存在序列相关性，且收益可能与风险存在关系，因此，在GARCH(1,1)模型的均值方程中引入AR项与波动项，表达式如下：

(3)

上述模型的方差方程中不能反映出信息的非对称性冲击.

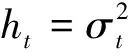
(4)

等式左边为条件方差的对数，这样可以将杠杆的影响转化为指数的形式，由于指数的取值最小就是0，这样可以保证条件方差的预测值是一个非负的数，放宽了模型的使用条件.杠杆效应是否存在能够通过模型(4)最后一项的系数γ<0的假设检验.只要拒绝假设条件γ=0，就可以得出存在非对称性影响.

使用的模型(AR-EGARCH-M)如式(5)所示.

(5)

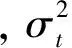
2．2 数据选取

上证综合指数是中国最早发布的指数，是以上证所挂牌上市的全部股票为计算范围，主要为大中型上市企业，上证指数对中国股市的发展具有较强的代表性，选取上证指数来分析中国股市波动的非对称性发展情况.其时间跨度为1991年1月2日-2013年12月31日上证指数收盘价数据，共2 052个样本观测值，数据来源于国泰安数据库.

对上证指数日收盘价的对数收益，即

rt=ln(pt)-ln(pt-1).

收益率为1+rt=pt/pt-1，得ln(1+rt)=ln(pt)-ln(pt-1)，由泰勒展开式得到ln(1+rt)≈rt，其中，ln(pt)为在t时的对数盘点数；rt为日收益率.

使用Eviews6进行数据分析与处理.图1显示了1991-2013年上证指数及其收益率的变化趋势.上证指数收益率在20世纪90年代早期与中期具有较大的波动性，1997年以后，收益率的波动性逐渐变小，但在2008-2010年又有所上升.

图1虽然能在一定程度上反映上证指数及其收益率的波动性，但这种波动性的非对称性如何，需要进一步的模型分析.

3 实证分析

3．1 收益率序列基本特征

从上证指数的收益率序列能明显看出，其波动性明显存在着一定的集中性，具有着波动的集聚性特点，即波动大的区间较波动小的区间之间存在明显的区别.

从1991～2013年上证指数收益率序列相关统计量来看，上证指数收益率存在明显的尖峰厚的分布特征，JB统计量较高，在5%的显著性水平下均拒绝序列服从正态分布的假定.

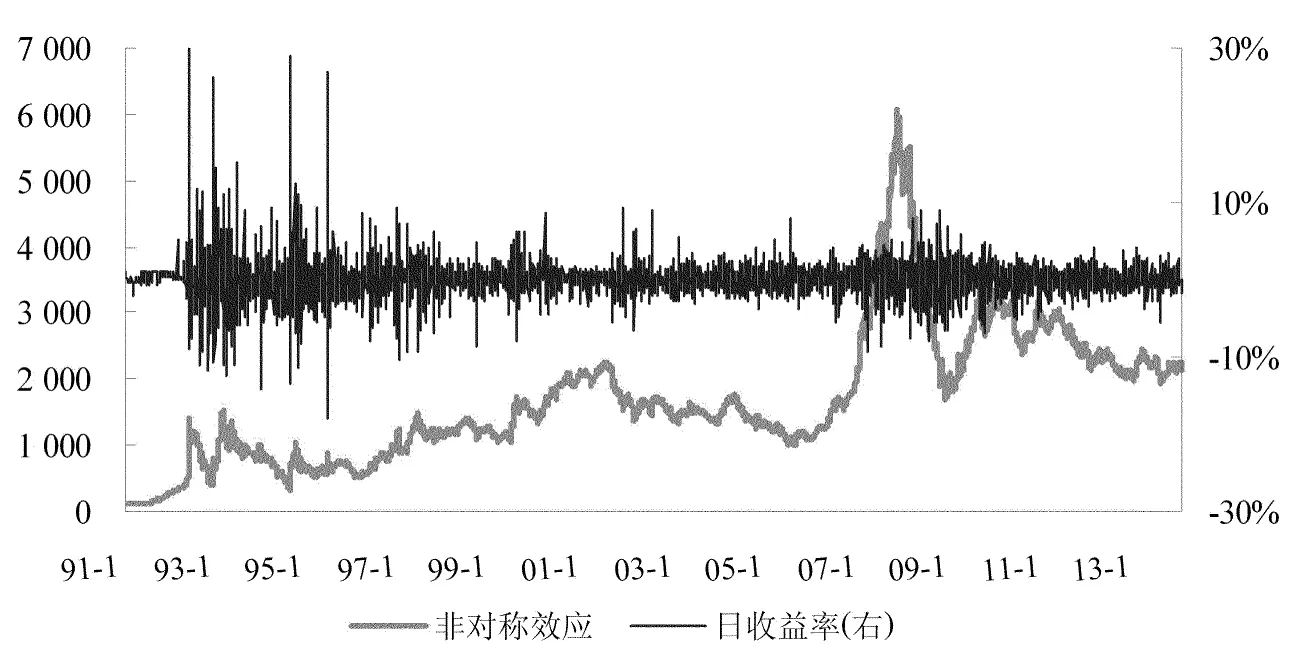
图1 1991～2013年上证指数及收益率

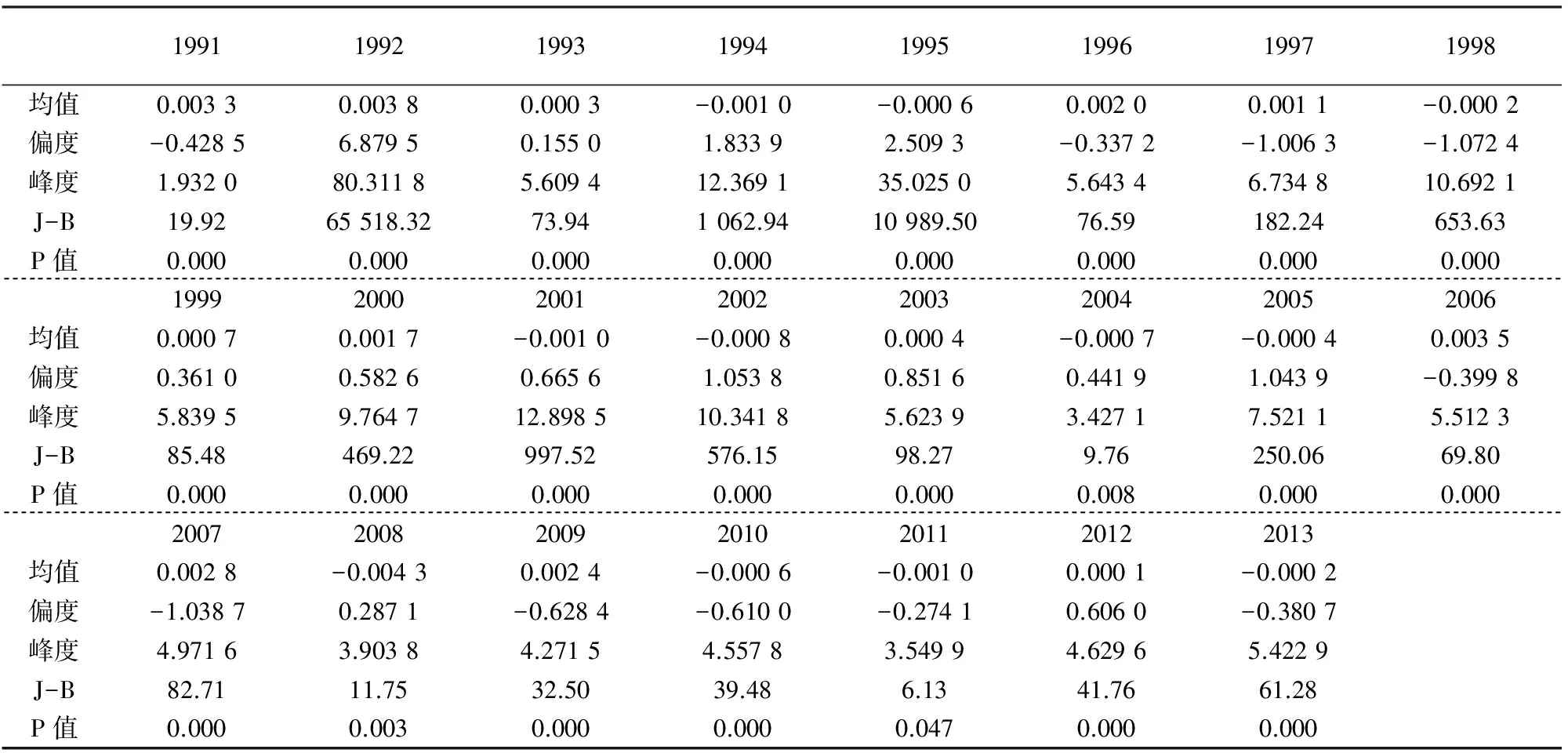
19911992199319941995199619971998均值0．00330．00380．0003-0．0010-0．00060．00200．0011-0．0002偏度-0．42856．87950．15501．83392．5093-0．3372-1．0063-1．0724峰度1．932080．31185．609412．369135．02505．64346．734810．6921J-B19．9265518．3273．941062．9410989．5076．59182．24653．63P值0．0000．0000．0000．0000．0000．0000．0000．00019992000200120022003200420052006均值0．00070．0017-0．0010-0．00080．0004-0．0007-0．00040．0035偏度0．36100．58260．66561．05380．85160．44191．0439-0．3998峰度5．83959．764712．898510．34185．62393．42717．52115．5123J-B85．48469．22997．52576．1598．279．76250．0669．80P值0．0000．0000．0000．0000．0000．0080．0000．0002007200820092010201120122013均值0．0028-0．00430．0024-0．0006-0．00100．0001-0．0002偏度-1．03870．2871-0．6284-0．6100-0．27410．6060-0．3807峰度4．97163．90384．27154．55783．54994．62965．4229J-B82．7111．7532．5039．486．1341．7661．28P值0．0000．0030．0000．0000．0470．0000．000

3．2 平稳性与序列相关检验

用ADF单位根检验法来检验上证综合指数收益率序列的平稳性.由收益率序列的基本统计分析可知：收益率序列围绕在均值周围波动，不存在着明显异于均值的趋势.因此选择了不带时间趋势的回归模型来进行单位根检验，其结果见表2.可以看出，1991-2013年上证指数收益率序列均是平稳的；通过收益率序列的AC图和PAC图分析，可以直观的看出某些年份的自相关和偏自相关数据都有一部分统计上显著异于0，同时可以观察到诸多滞后的Ljung-Pierce Q检验都是显著的，表明序列存在自相关性，也有某些年份序列不存在自相关，通过OLS回归，给出了序列可能的自相关阶数，见表2的AR项.

序列的条件异方差一般通过ARCH-LM方法进行检验，也可直接通过ARCH类模型的拟合系数进行判断，如果EGARCH模型中的EGARCH项通不过检验，即判断不存在条件异方差.

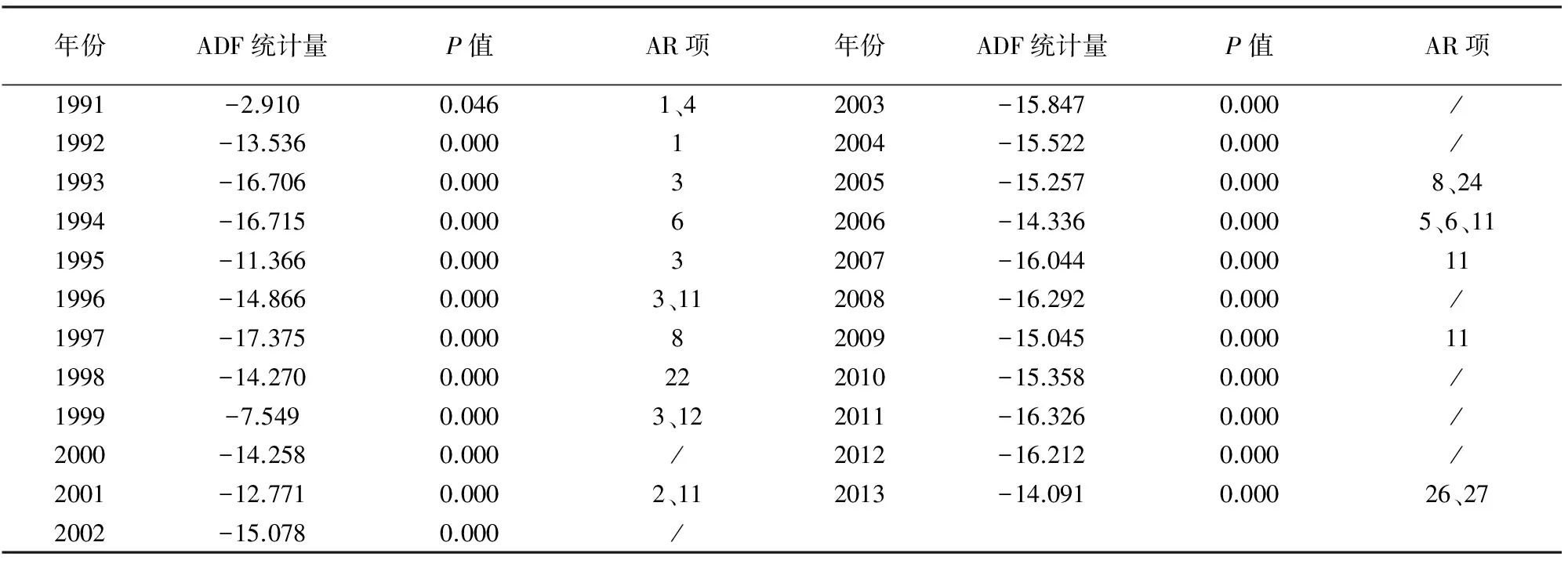
表2 1991～2013年上证指数收益率序列平稳性与序列相关检验

3．3 模型试验与阶段划分

对1991～2013年上证综合指数收益率序列进行AR-EGARCH-M模型拟合，其中，只有1994、2000、2002、2007、2009年收益与条件方差存在显著的关系，1994年与2002年条件方差的系数为负，即更大的波动反而会减少收益，2007与2009年均为正，即收益对风险有一个正的补偿，说明近几年股市的有效性较以往有所提高.发现1991、2010、2011年序列不存在条件异方差或者条件异方差不显著.下表为经AR-EGARCH-M模型拟合的每年的非对称效应：

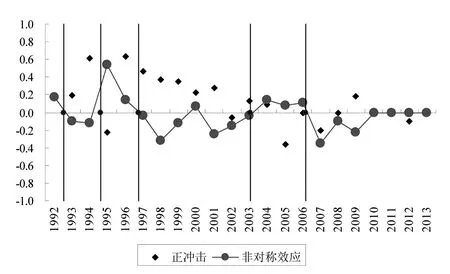
图2 1991～2013年上证指数收益率序列非对称效应

图2显示，上证指数收益率序列非对称效应呈现出一定的阶段性，如1993～1994年上证指数收益率序列受负冲击的影响要大于受正冲击的影响，而1995～1996年上证指数收益率序列受负冲击的影响要小于受正冲击的影响.将上证综合指数划分为6个大的序列阶段对非对称效应进行进一步分析.以年为单位，第一阶段R1为1991～1992年，第二阶段R2为1993～1994年，第三阶段R3为1995～1996年，第四阶段R4为1997～2003年，第五阶段R5为2004～2006年，第六阶段R6为2007～2013年.上证指数收益率序列受信息冲击的影响随着时间的推移越来越小，从某种程度上说明A股市场的有效性水平得到提高.

3．4 进一步建模与分析

与上述步骤基本相同，首先分析6个阶段上证综合指数收益率序列的基本特征，如表3所示.可以看出，6个序列均存在尖峰厚尾的特征，且明显不呈正态分布.

对序列的平稳性、序列相关性、1阶ARCH效应进行检验，单位根检验结果显示R1～R6均为平稳序列且均存在条件异方差，但存在不同阶数的自回归性，检验结果如表4所示：

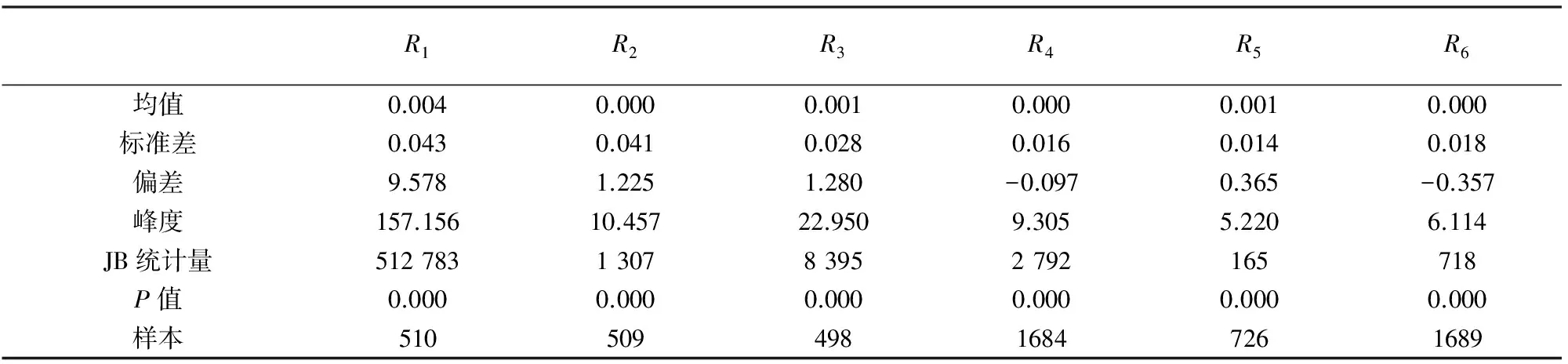
表3 阶段R1～R6上证指数收益率序列相关统计量

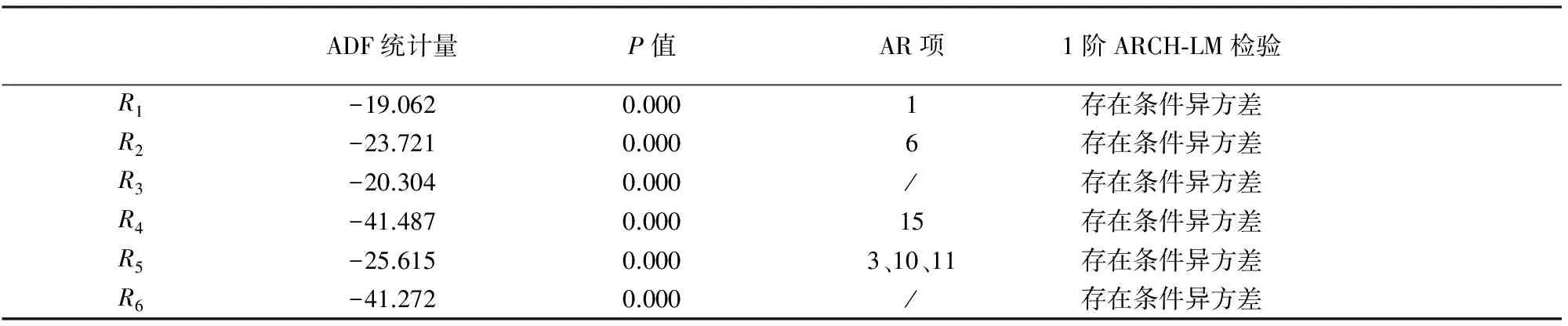
表4 阶段R1-R6上证指数收益率序列平稳性、序列相关、ARCH效应检验

对序列R1-R6进行AR-EGARCH-M模型拟合，发现所有序列的M项均不显著，予以剔除，最终模型及结果如表5所示．

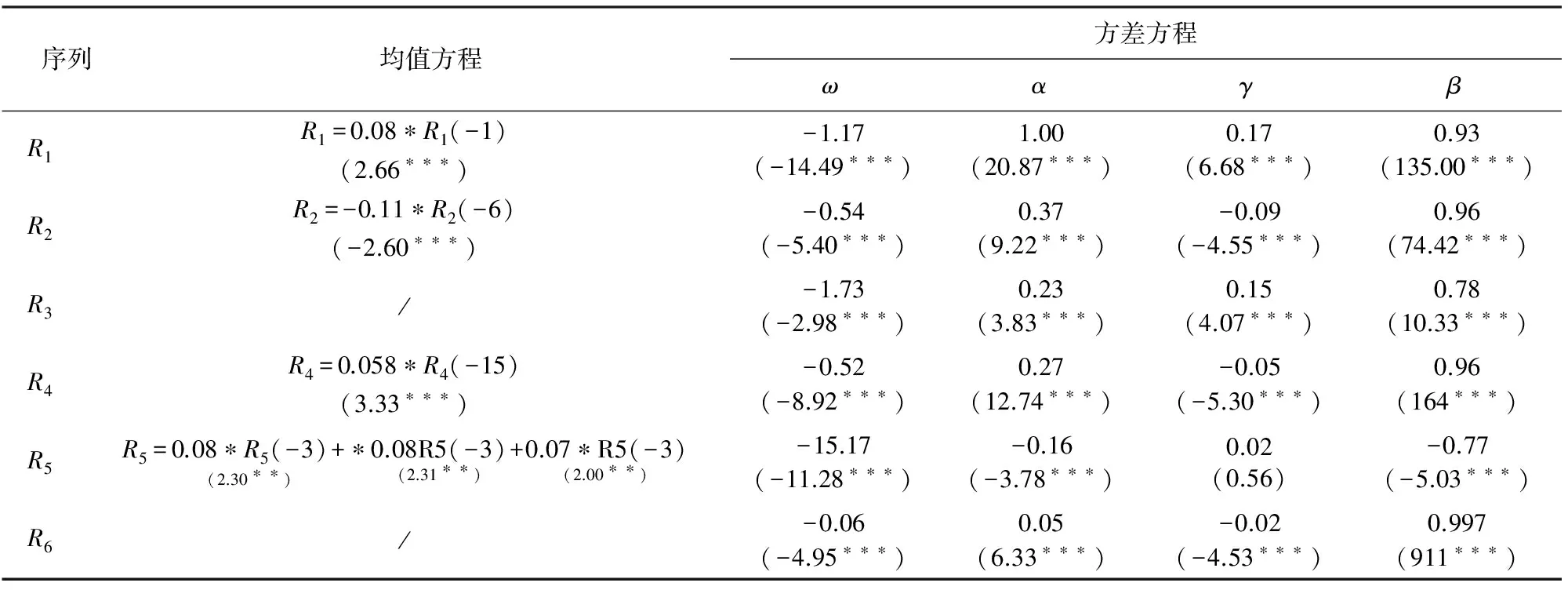
表5 阶段R1-R6信息冲击非对称效应测度最终模型

注：()中为z统计量，***，**表示在1%，5%下显著.

对比以上6个模型，除了第5阶段效应不显著外，其它序列的非对称效应均在1%下显著；对比α项可知，第一阶段为1.00，第二阶段为0.37，第三阶段与第四阶段为0.23、0.27，第6阶段为0.05，发现上证指数收益率受信息冲击的强度越来越小，表明中国A股市场的投机活动有较大程度的下降，规范化、有效性水平呈不断提高趋势；从非对称性冲击来看，第一阶段A股市场受到正冲击的影响为1.00，而受到负冲击的影响为0.83(1.00-0.17)，受负冲击的影响小于受正冲击的影响，第二阶段受负冲击的影响(0.48)大于受正冲击的影响(0.37)，第三阶段受负冲击的影响(0.08)小于受正冲击的影响(0.23)，第四阶段受负冲击的影响(0.32)大于受正冲击的影响(0.27)，第5阶段不显著，第6阶段受负冲击的影响(0.07)大于受正冲击的影响(0.05)，可以看出，A股市场受冲击的影响存在一个反复调整的过程．在早期股市，这种调整的周期比较短，随着A股市场的不断完善，有效性水平提高，调整的周期也相应地拉长.

建模之后，需要对模型的参数与残差进行检验.对估计系数检验，均值方程中的估计系数经过了Wald系数均不为零的检验，故此可以得到均值方程的估计是有效.

进一步对残差进行检验.Q统计相关图的检验结果显示Q统计量均在2倍标准差的范围之内.残差ARCH-LM检验结果如表6所示.结果显示除了第五阶段外(在10%的显著性水平下存在条件异方差，但不存在非对称效应)，其他阶段上证指数收益率序列F和Obs*R2的统计量均不显著，表明了标准残差不存在额外的ARCH效应，表明方差方程通过残差检验，模型有效.

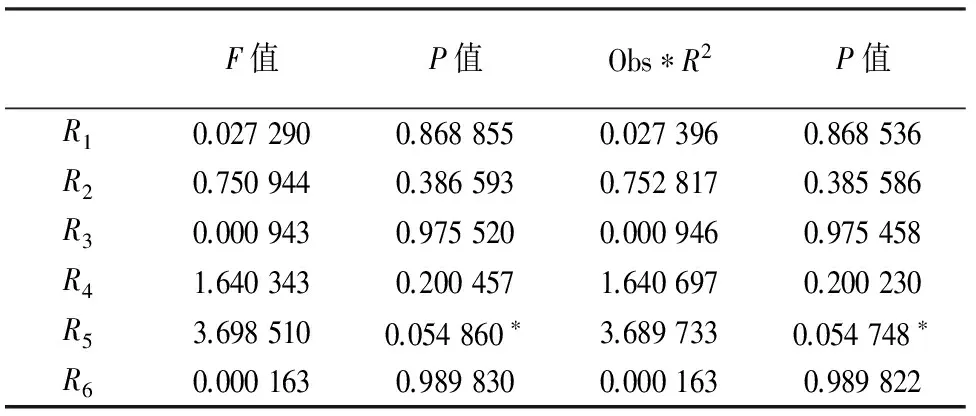
表6 EGARCH模型拟合后的ARCH-LM检验

4 结 论

采用AR-EGARCH-M模型对中国A股市场上信息对收益率波动的非对称性影响进行实证研究.首先，对每一年上证指数收益率序列的非对称效应进行分析，将自1991年至2013年的A股市场划分为6个阶段，其中第一阶段为1991～1992年，第二阶段为1993～1994年，第三阶段为1995～1996年，第四阶段为1997～2003年，第五阶段为2004～2006年，第六阶段为2007～2013年.

研究结果表明：A股市场不仅存在明显负杠杆效应，也存在正杠杆效应，而且正负杠杆效应交替出现，表现出信息不对称性，但是随着时间的推移，这种不对称性明显减小.表明中国股票市场的投机成分不断减少、投资者不断趋于理性．

在前面4个阶段，中国股票市场波动十分剧烈，总体风险较大，上证指数收益率受信息冲击的强度较大，尤其是在第一、第二阶段，即1991～1994年.这一时期股票市场的发行和交易缺乏全国统一的规范，缺乏统一的法律法规和集中监管.因尚未形成完善的供求机制与市场监控机制，高速发展的股市暴露了许多问题，股市价格的暴涨暴跌，投资者的投资理念不强，其投资行为极易受到各种非理性因素的影响.

在后面2个阶段，A股市场波动的非对称性明显下降，尤其是第6个阶段，受负冲击的影响(0.07)，受正冲击的影响(0.05)，信息冲击对股市的影响较前几个阶段小了很多，这种情况与2005年5月开始的股权分置改革存在较强的吻合.股权分置在很多方面制约了中国资本市场其规范发展和国有资产管理体制的根本性变革，中国股票市场成熟程度在近些年有了较大提高.

股票市场作为宏观经济的“晴雨表”，有着非常重要的作用，股票市场的成熟有利于提高直接融资的比例，降低实体经济对银行体系的依赖；同时加快了企业的经营体制的改革，建立现代企业制度，有利于提高公司的竞争力；通过股票市场的价格发现机制实现资源的优化配置；股票市场不仅给投资者和融资者提供了投融资渠道，也提供分散风险的途径.可以推测，随着中国A股市场的不断成熟，其将在经济中发挥更重要的作用.

[1] ENGLE R F, BOLLERSLEV T.Modeling the Persistence of Conditional Variances[J]. Econometric Reviews, 1986,5(1):21-30.

[2] Nelson, Daniel B. Conditional Heteroscedasticity Asset Return: A New Approach[J]. Economitrica, 1991, 59(2):350-368.

[3] 徐林,祝东进.股市投资回报过程的长相依性与风险度量[J].经济数学，2013:30(1)：50-53.

[4] 王璐.股市和债市波动溢出马尔科夫体制转换特征的数量研究[J].经济数学，2013:30(2)：78-84.

[5] 任彪,李双成.中国股票市场波动非对称性特征研究[J]. 数学的实践与认识. 2004(9): 63-68.

[6] 何帮强,惠军.基于ARMA-EGARCH-M模型的沪深股市波动性分析[J].合肥工业大学学报(自然科学版).2007(7): 864-868.

[7] 陈潇,杨恩.中美股市杠杆效应与波动溢出效应——基于GARCH模型的实证分析[J].财经科学.2011(4):17-25.

[8] 杜莉萍.基于ANN-EGARCH模型的沪深300指数波动趋势预测[J].生产力研究.2013(2):58-61.

[9] 陈浪南,黄杰鲲.中国股票市场波动非对称性的实证研究[J].金融研究.2002(5):67-73.

[10]韩贵,王静.基于EGARCH模型的中国股市信息对称性研究[J].西南交通大学学报(社会科学版).2008(4): 107-112.

[11]朱东洋,杨永.中国股市波动的非对称性和杠杆效应研究[J].技术经济.2010(9).

[12]蔡晓春,邹克.基于ARCH类模型的人民币汇率波动特征比较[J].统计与决策, 2012(13):152-156.

Asymmetry Analysis of Stock Market Information Impact Based on Stages

ZHOU Yu
(Hunan Vocation College of Modern Logistics, Changsha, Hunan 410000，China)

This paper analyzed the asymmetry of information impact using Shanghai Composite Index yields sequence in 1991-2013 based on AR-EGARCH-M model. First, this paper analyzed the asymmetry characteristics of information impact on Shanghai Composite Index in the years; then Shanghai Composite Index was divided into six stages for further analysis. The results showed that A stock market showed asymmetric information, and that positive and negative leverage of information impact appeared alternately. However, the asymmetry was significantly reduced at present. This suggests that speculative elements of China stock market continue to decrease, investors are becoming more rational, and the level of effectiveness of the A-share market are being improved.

investment; Shanghai Composite Index; asymmetry; AR-EGARCH-M; Information shock

2015-03-09

周 宇(1982—)，女，湖南长沙人，统计师、讲师，硕士 E-mail:8857025@qq.com

F830

A