立交匝道桥地震响应及合理抗震体系研究

张菊辉，管仲国

(1.上海理工大学 环境与建筑学院，上海 200093;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

组建纵、横、环向交错的高架快速交通网络是现代大型城市缓解交通压力的有效途径，为了实现不同高架干线之间，以及高架线路与地面道路之间的互通，各种立交匝道必不可少。受城市用地以及周边环境的限制，立交匝道桥一般具有小曲率半径、大纵坡等特点。这使得匝道桥在平面和立面布置上，都有很强的非规则性［1］。因此，在地震作用下，往往容易遭到损坏。美国SR14/I5立交枢纽在1971年的San Fernando地震和1994年的Northridge地震中均发生落梁破坏，并切断下行线路交通［2－3］;2008 年，汶川地震中，百花大桥、回澜立交匝道桥2座小半径曲线梁桥也发生了垮塌、严重阻碍了震后的救灾进程［4－5］。由此可见，确保立交匝道桥的抗震安全性对于提高整个城市主要交通网络的灾后可通行能力具有非常重要的意义。

迄今为止，已有部分学者进行了有关匝道的抗震研究及结构性能评估。Zureik等［6］总结了平面曲线布置对I型钢梁桥抗震性能的影响;毕桂平等［7］就大型复杂立交工程中匝道桥的合理抗震分析模型进行了探讨;张永亮等［1］针对一座实际匝道桥工程，基于新规范体系进行了两级设防地震下的结构抗震性能评估;王东升等［5］总结了汶川地震桥梁震害经验，指出了曲线桥中的矮墩因地震惯性力较大，极易发生弯剪等低延性破坏;管仲国等［8］针对某城市平行匝道桥，分别采用延性抗震体系和减、隔震体系进行设计，指出采用减、隔震体系可使结构具有更优的抗震性能。

本文在上述研究的基础上，以上海嘉闵高架桥工程为依托，系统分析了曲率半径、地震输入方向对结构地震响应的影响，并基于新规范体系［9］，总结了立交匝道桥在两级设防地震下的结构性能一般规律表现，在此基础上，进一步探讨了结构抗震体系的设计策略。

1 桥梁概况与结构建模

以上海嘉闵高架桥建设工程为依托，选取典型互通立交匝道桥。跨径布置为2×30+3×30+3×30 m连续梁;桥面纵坡6%。上部结构为预制小箱梁，桥宽8.5 m(图1);下部结构为1.5 m×2 m的矩形截面独柱墩，倒T形盖梁，基础为桩基，桩径0.8 m，桩长40 m。场地类别为四类软土场地，整体稳定性较好，可不考虑软土震陷影响。地震设防烈度7度，设计基本加速度为0.1 g，场地系数 1.4，特征周期 0.65 s。E1、E2 两级地震下的结构抗震重要性系数分别为0.5和1.7，图2为两级水平地震动反应谱。根据连续梁桥的特点，建立结构三维有限元动力分析模型。主梁、盖梁、墩均采用空间梁单元模拟，二期恒载模拟为附加分布质量，承台模拟为质点，桩基采用等效土弹簧模拟桩土相互作用［10］。为分析平面曲线布置对结构地震响应的影响［11］，本文分别构建了曲率半径为 50 m、100 m、150 m、200 m、250 m以及∞(直线桥)六种模型，图3所示为曲率半径50 m的有限元模型示意，起始处1#为桥台，2#～9#墩柱高度范围为 2.8 ～15.4 m，且 9#墩与主线相连。此外，为考虑地震输入方向的影响，按30°级差，进行了12个输入方向下的地震响应分析。

2 匝道桥地震响应分析

图1 匝道桥桥梁结构示意Fig.1 Structure oframp bridge

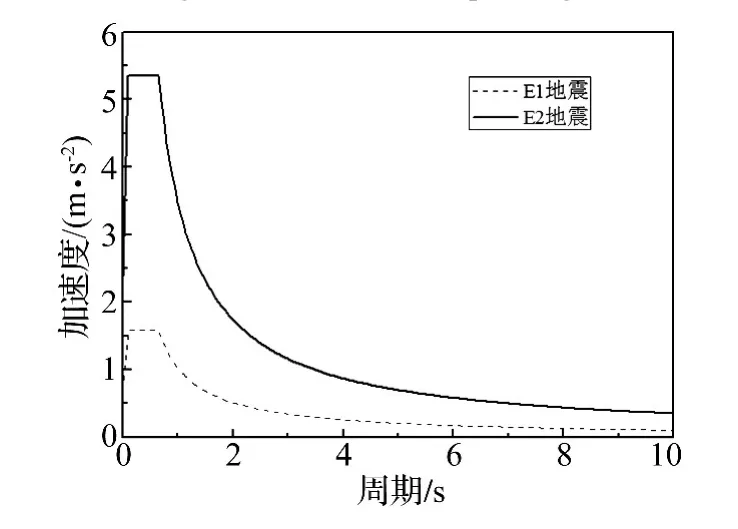
图2 设计反应谱Fig.2 Design spectrum

图3 匝道桥的有限元模型(曲率半径R=50 m)Fig.3 Finiteelement model of ramp bridge(curve radius R=50 m)

首先，采用弹性反应谱分析方法，分析曲率半径和地震输入方向对结构弹性地震响应的影响，进而基于两级设防水准下的关键截面能力需求比分析，判别结构在E1、E2两级设防地震下的性能状态。

2.1 曲率半径的影响

图4所示为各桥墩在不同曲率半径下的各墩最大弹性地震响应。从图中可以看出，切向上的地震响应主要表现在固定墩上，最低墩的水平剪力最大。而墩底弯矩先随墩高的增加而增加，但达到一定幅度时即趋于稳定;在法向上，由于各墩均为固定约束，各墩地震响应的连续性相对较好，最大剪力响应发生在矮墩区，最大弯矩响应则在高墩区，此外，过渡墩处的响应一般比连续墩处的更大。考虑不同曲率半径的影响，50 m半径工况墩底切向弯矩比直桥低约15.6%，其余工况则相差不超过5%;在法线方向上，50 m半径工况与直桥相比，墩底剪力最大相差达46.42%(5#墩)，墩底弯矩最大相差达－17.96%(3#墩)，而当曲率半径达到150 m，墩底剪力和墩底弯矩最大相差均不超过10%。

由此可见，对于曲率半径较大的匝道桥，可直接采用直线桥的分析结果。目前，我国《公路桥梁抗震设计细则》［9］和《城市桥梁抗震设计规范》［12］均规定曲率半径大于20倍桥宽的桥可视为规则桥梁。对于匝道桥，既有平面曲线布置的影响，同时也有大纵坡带来的墩高差异，因此并不能简化为规则桥，但从本文的分析结果上看，当满足曲率半径大于20倍桥宽时，可简化为直线桥进行分析。

图4 不同曲率半径下的墩底最大地震响应(E1地震作用)Fig.4 Maximum seismic response at the pier bottom under different curve radii(E1 earthquake)

2.2 地震动输入方向影响分析

图5、6所示分别为不同地震激励方向下的各墩位的切向墩底弯矩、法向墩底弯矩响应，其中水平轴为地震激励方向与各墩切线方向的夹角。从图中可以看出，不同的地震动输入方向对墩底弯矩影响显著。在小曲线半径条件下(R=50 m)，对应桥墩切向最大弯矩，最不利输入方向与桥墩切向的最大偏角约为21°，按切向输入所得的弯矩响应与最不利弯矩低约7.2%，而对应法向最大弯矩，最不利输入方向与桥墩法向的最大偏角可达31.2°，按法向输入所得的弯矩响应与最不利弯矩低约18.4%。而当曲率半径较大(R=250 m)时，无论是切向还是法向，墩底弯矩与输入角度之间的对应关系均符合较好(图5(b)和图6(b))。由此可见，小曲率半径匝道桥的地震响应较为复杂，即使按墩柱切向、法向方向的地震输入仍可能低估其地震响应。

图5 不同地震激励方向下的各墩墩底切向弯矩(E1地震作用)Fig.5 Tangential moment at the pier bottom Vs different earthquake input directions(E1 earthquake)

图6 不同地震激励方向下的各墩墩底法向弯矩(E1地震作用)Fig.6 Normal Moment at the pier bottom Vs different earthquake input directions(E1 earthquake)

2.3 两水准设防下的结构性能状态

图7 各计算工况下的墩柱抗弯能力需求比Fig.7 Capacity/demand ratio of pier columns under different curve radii

图7给出了各工况下墩柱墩底截面在E1、E2两级地震作用下的抗弯能力需求比。其中，墩柱纵筋配筋率为1.25%，箍筋体积配箍率4‰，桥墩抗弯能力采用截面等效屈服弯矩。从图中可以看出，在E1地震作用下，各墩柱无论在切向还是法向上，其抗弯能力需求比均超过1.5，表明各墩柱均将处于弹性工作状态，且有一定的安全度。而在E2地震作用下，各联固定墩切向弯矩，以及高墩区墩柱的法向弯矩，能力需求比均小于1，表明这些墩柱在E2地震作用下将进入塑性状态。其中2#墩由于墩身高宽比仅为1.87，参照美国Caltrans规范［13］进行验算，结果表明剪切破坏将先于弯曲破坏，因此难以利用墩柱延性进行抗震。

由此可见，匝道桥较容易满足E1地震下的强度要求，但在E2地震作用下，顺桥向制动墩以及高墩区在横桥向均易进入屈服，其中较矮的制动墩还较易产生弯剪或者剪切破坏。

3 结构抗震体系设计策略

前述分析表明，立交匝道桥结构平面、立面布置均较为复杂，不同墩高处的结构抗震性能差异较大。延性抗震体系和减、隔震体系是两种基本的结构抗震体系，为优化匝道桥结构抗震体系设计，本文选取曲率半径R=∞时的直线匝道桥模型，分别按延性抗震体系和减、隔震体系进行设计。其中延性设计体系采用普通盆式支座，主从约束模拟;减、隔震体系采用铅芯橡胶支座J4Q520×520，双线性本构关系模拟［14］。地震输入为3条根据目标谱拟合的人工波，分析方法为非线性时程分析。

3.1 延性抗震体系

根据前述分析，延性抗震体系中，在E2地震作用下，2#、5#、8#固定墩在纵向地震输入下，以及 6# ～8#墩在横向地震输入下，将进入塑性状态。选择各墩潜在塑性铰部位为墩底，设置墩底集中塑性铰单元，采用非线性时程分析方法，进一步对墩身延性能力进行检算。结果显示:除2#墩(剪切破坏)以外，其余墩位处的位移延性能力/需求均大于1.3，满足性能目标要求。

图8 桩基布置方案(单位:mm)Fig.8 Pile layouts(unit:mm)

延性体系的基础部分按能力保护原则进行设计，即对未进入延性的墩柱，基础受力直接采用弹性地震响应结果，已进入延性状态的墩柱，基础受力考虑1.2的超强系数，按能力保护原则进行确定［15］，结果见表1。其中，基础布置方案考虑两种，如图8所示，其中5根桩是常规荷载所必需的桩数，延性设计中单桩的配筋率为2%。可以看出，5根桩无法满足基础的强度需求，6根桩布置仅可满足4#～8#的基础强度需求，2#～3#墩则无法满足。由此可见，矮墩区不宜采用延性抗震体系。

表1 延性抗震体系下的单桩能力需求比Tab.1 Pile C/R ratios for ductile system under E2 earthquake

3.2 减隔震体系

减隔震设计中，除减隔震支座以外，主体结构各部分均应保持弹性［8，16］。铅芯橡胶支座 J4Q520×520的本构关系按双线性考虑，具体性能参数如表2所示。采用非线性时程分析方法对减隔震体系的地震响应进行分析。按前述配筋方案，对各墩底关键截面的抗弯承载力进行验算，结果如图9所示。可以看出，矮墩区的墩柱能力可以得到很好地满足，其中2#墩柱的抗剪承载力也可满足。但在高墩区，各墩抗弯承载力能力需求比接近于1，仍存在结构进入塑性状态的较大风险。

表2 铅芯橡胶支座基本参数Tab.2 Mechanical properties of LRBs

单桩强度的检算如表3所示，可以看出，桩数较少的5根桩方案，可以满足2#～6#墩位的基础强度检算，7#～8#墩位则需要采用6根桩方案。此外，所有减隔震支座的侧向地震位移均不超过±100mm(表4)。J4Q520×520铅芯橡胶减隔震支座，橡胶层总厚度为66mm，支座极限变形可达±165mm(按250%极限剪应变计)，可满足变形验算要求。由此可见，减隔震体系更适宜用于矮墩区。

图9 减隔震抗震体系墩底地震响应Fig.9 Seismic response at the pier bottom under the isolated seismic resistant system

表3 减隔震体系下的单桩能力需求比Tab.3 C/R ratios of the piles for isolated seismic resisting system under E2 earthquake

表4 支座位移(减、隔震设计)Tab.4 Bearing displacement(isolated seismic resisting design)

3.3 抗震设计方案优选

通过以上两种抗震体系对比，可以看出使用任何一种单一的抗震体系都不能很好地满足预期的性能要求。相反，在矮墩区选用减隔震体系、而在高墩区选用延性抗震体系，则可较好地融合两种体系的优点，既可避免矮墩的剪切脆性破坏和基础内力需求过大的问题，又可以充分发挥柔性高墩的延性潜力。事实上，匝道桥由于一条线上的墩高差异较大，不同的墩高对结构的动力特性有直接地影响，因此简单按一种体系显然并不合适。为此，建议按不同的墩高采用不同的抗震体系，具体如表5所示。

表5 抗震体系建议方案Tab.5 Proposed seismic resistant system

4 结论

本文以上海嘉闵高架某一主线立交匝道为研究对象，分析了不同曲率半径、地震动输入方向对立交匝道桥地震响应的影响，指出小曲率半径下的匝道桥地震响应较为复杂，地震最不利输入方向与墩柱切线、法线方向仍存在20°～30°的偏差，墩底弯矩偏低约10% ～20%;大曲率半径下的匝道桥地震响应与直桥基本一致，可简化为直线桥进行抗震分析。并基于新规范体系，评估了立交匝道桥在两级地震作用下的性能，指出匝道桥较容易满足E1地震下的强度要求，在E2地震下，顺桥向固定墩以及横桥向高墩均会进入屈服，其中矮墩固定墩较容易发生剪切破坏。在此基础上，针对直线匝道桥模型，分别采用延性抗震体系与减、隔震体系进行抗震设计优化，并评估其适用性，指出单独采用任何一种抗震体系都难以满足结构性能要求，建议高墩区采用延性抗震体系，矮墩区采用减隔震体系。

［1］张永亮，徐聪，陈兴冲.城市曲线匝道桥有限元建模及抗震性能评估［J］.兰州交通大学学报，2013，32(1):1－4.ZHANG Yong-liang，XU Cong，CHEN Xing-chong.The seismicperformance evaluation and finite element modeling for urban curved ramp bridges［J］.Journal of Lanzhou Jiaotong University，2013，32(1):1 －4.

［2］Tseng W S，Penzien J.Seismic analysis of long multiple-span highway bridges［J］.Earthquake Engineering and Structural Dynamics，1975(4):3 －24.

［3］Tseng W S，Penzien J.Seismic response of long multiple-span highway bridges［J］.Earthquake Engineering and Structural Dynamics，1975(4):25 －48.

［4］王东升，孙治国，郭迅，等.汶川地震桥梁震害经验及抗震研究若干新进展［J］.公路交通科技，2011，28(10):44－53.WANG Dong-sheng，SUN Zhi-guo，GUO Xun，et al.Lessons learned from Wenchuan seismic damages and recent research on seismic design of Highway Bridges［J］.Journal of Highway and Transportation Research and Development，2011，28(10):44－53.

［5］王东升，孙治国，李晓莉，等.汶川大地震曲线梁桥震害及破坏机理分析［J］.防灾减灾工程学报，2010，30(5):572－579.WANG Dong-sheng，SUN Zhi-guo，LIXiao-li，et al.Seismic Damage investigation and failure mechanism analysis of curved bridges in Wenchuan earthquake［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30(5):572－579.

［6］Zureick A，Naqib R.Horizontally curved steel I-girders:state-of-the-art analysis methods［J］.Journal of Bridge Engineering，1999，4(1):38－47.

［7］毕桂平，江涌.大型复杂立交工程中匝道桥抗震分析计算模型研究［J］.桥梁建设，2003，44(6):15－17.BI Gui-ping，JIANG Yong.Study of calculation model for seismicanalysis of ramp bridges of large and complicated interchange projects［J］.Bridge Construction，2003，44(6):15－17.

［8］管仲国，李建中.城市高架桥合理抗震体系选择与经济性对比［J］.地震工程与工程振动，2011，31(3):91－98.GUAN Zhong－guo， LI Jian－zhong. Selection andcost comparison of proper seismic resisting systems for urban viaducts［J］. Journal of Earthquake Engineering and Engineering Vibration，2011，31(3):91－98.

［9］JTG/T B02－01－2008公路桥梁抗震设计细则［S］.北京:人民交通出版社，2008.

［10］葛继平，管仲国，李建中.群桩基础桥梁抗震分析简化模型［J］.结构工程师，2006，22(6):64－67.GE Ji－ping，GUAN Zhong－guo，LI Jian－zhong.Simplified model for seismic analysis of bridges with group pile foundations［J］.Structural Engineers，2006，22(6):64－67.

［11］Katsushi l， Hiroyuki O， Gunji A，et al. A study on preventing the fall of skew and curved bridge decks by using rubber bearings［J］.Structural Engineering and Mechanics，2001，12(4):347－362.

［12］CJJ166－2011城市桥梁抗震设计规范［S］.北京:中国建筑工业出版社，2011.

［13］ Seismic Design Criteria， Version 1.1， Sacraments，California，California Department of Transportation(CALTRANS)，Division of Structures，1999.

［14］Najm H，Patel R，Nassif H.Evaluation of laminated circular elastomeric bearings［J］.Journal of Bridge Engineering，2007，12(1):89－97.

［15］范立础，卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001.

［16］范立础，王志强.桥梁减隔震设计［M］.北京:人民交通出版社，2001.