集中驱动式纯电动车抖动分析及主被动控制研究

于 蓬，章 桐，3，王晓华，郭 荣

(1.同济大学 新能源汽车工程中心;2.同济大学 汽车学院;3.同济大学 中德学院，上海 201804)

纯电动车的动力总成多采用电机－变速器集成驱动的形式，整个动力传动系统没有离合器等分离装置［1］。这种结构上的常啮合，加之驱动电机快速的动态响应，使动力总成悬置系统绕扭矩轴方向的振动与传动系统的扭转振动耦合在一起，构成电动车瞬态振动的新特性［2］。Moriya等［3］用“surge”来定义电动车由于电机转矩迅速变化引起的抖动现象，并提出通过控制电机输入参考转矩的方法衰减传动系统的扭转振动。Amann等［4］也认为通过控制电机达到衰减振动的目的是机电一体化设计的好例子，优于添加扭转减振装置等机械手段。之后，考虑电机动态、齿间侧隙及半轴柔性，建立传动系统的简化模型并进行主动控制，成为各大研究院所和汽车厂商解决电动车抖动问题时所采用的主要手段［5－6］。当然，也有直接从悬置系统瞬态振动的分析和优化方面入手进行的研究，如文献［7－8］在面对某集中驱动式燃料电池车的瞬态振动问题时所采取的措施。工程实现方面，国内较为普遍的做法是利用开环相位叠加的控制方法改善整车控制器的输出参考转矩，可以获得较好的驾乘舒适性，但是其标定工作繁杂，对动力性能的衰减也很明显［9］。将传动系统的主动控制与悬置系统的被动优化相结合，是目前研究的热点，文献［10］在考虑电机激励主动控制的基础上对动力总成悬置系统进行了优化，但是所建立的整车14自由度悬置系统－整车模型，并未考虑转子－齿轮系统的传动特性，有待进一步完善。

在以往研究的基础上，从某电动车的瞬态抖动这一工程问题入手，搭建能够综合反映电动车常啮合和振动耦合特性的整车多体动力学仿真平台，进行基于传动系统扭转振动主动控制和悬置系统优化的主被动控制研究。为改善该电动车的瞬态抖动问题，提高驾乘舒适性提供技术支持。

1 电动车抖动机理及传递路径分析

1.1 整车多体动力学模型

综合考虑动力总成内部转子－齿轮系统的传动关系，基于ADAMS/Driveline平台建立整车模型，如图1所示。模型包括动力总成及其悬置系统、转子－齿轮系统－半轴系统、双横臂式前悬架、齿轮齿条式转向机构及方向盘、双横臂式后悬架、基于魔术公式的轮胎模型及刚性车身，其中，转子－齿轮－半轴－车轮系统中的半轴考虑为弹性－集中质量模型。

图1 电动车整车模型Fig.1 Whole model of electric vehicle

利用整车多体动力学模型，在电机转子处施加驱动力矩，可对电动车瞬态抖动现象进行仿真，得到车身和动力总成质心三向加速度、悬置点三向动反力等信息。仿真曲线将在控制效果比较时一并给出，从其结果看电动车在瞬态工况下受到明显的冲击作用。车身质心x向加速度波动幅值较大，振幅达到3.352 m/s2，表现为整车的纵向抖动(整车坐标X方向)及竖直方向(Z向)的振动。

1.2 车身纵向抖动机理

定义整车坐标系:以汽车前轴中点为原点，指向汽车行驶方向后方为X轴正方向，指向驾驶员右侧为Y轴正方向，竖直向上为Z轴正方向。假设整车车身为刚性体，可用公式(1)～(4)描述车身质心纵向加速度、车身质心俯仰角加速度、车身质心横摆角加速度及驾驶员座椅底板处纵向加速度。

式中:H、W为地板加速度测点和车身质心的纵向、横向距离，M 为车身质量，Iyy、Izz为车身转动惯量，Fxi、Fyi、Fzi为连接点的载荷，Xi、Yi、Zi为连接点与车身质心的距离。i=1～5，分别代表前悬架控制臂、后悬架控制臂、前悬架减振器上支点、后悬架减振器上支点及动力总成悬置点，共5组关键点的作用。

1.3 抖动传递路径及贡献量

根据前述分析，引起车身纵向振动的主要路径如图2所示。

图2 纵向抖动传递路径Fig.2 Transfer path of longitude surge

在电动车整车模型的电机定转子间施加阶跃激励(取120 Nm)，得到电动车质心及各传递路径中关键点的三向动载荷响应;将各动载荷响应值代入式(4)，得到传递路径中各个关键点的纵向加速度分量，各分量求和即为车身总纵向加速度;各关键测点纵向加速度在车身总纵向加速度中的占比即为不同传递路径的贡献量，如图3所示。

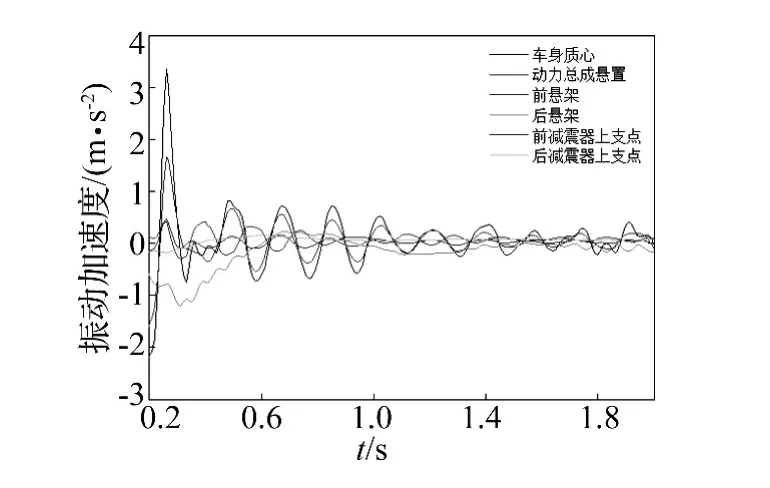
图3 车身纵向振动贡献量分析Fig.3 Contribution analysis of longitude surge

根据贡献量分析结果，路径2为引起车身纵向振动的最大贡献量传递路径，说明悬置系统在瞬态工况下受到较大的冲击，引发悬置系统瞬态振动和整车纵向抖动;而路径1中的电机动态响应为引发车身纵向振动的激励源;因此在解决该车抖动问题时，首先从路径1入手，采用主动控制的方法，减小电机动态响应对传动系统和悬置系统的冲击;然后从路径2入手，进行悬置系统的被动优化，进一步减小抖动现象。至于路径3对应的悬架系统优化，包括阻尼、刚度及侧倾角度等的优化，暂不涉及。

2 扭转振动主动控制

2.1 传动系统简化模型

所研究电动车采用典型的电机前置前驱动力传动方式，其电机－减速器/差速器驱动系统可简化为图4所示的弹性－集中质量系统。动力总成的集中驱动电机与减速器/差速器总成集成在一起，然后通过左右半轴驱动车轮，进而驱动车辆。

图4 传动系统简化模型Fig.4 Simplified model of drive train

其中:Jm为电机转子和减/差速器等效到电机转子端的等效转动惯量;Jw为车轮转动惯量;Kd为驱动半轴扭转刚度;ωm为电机转子机械角速度;Tm为电机转矩。K表示是否考虑齿间侧隙，K闭合表示不考虑齿间侧隙，K开启表示考虑齿间侧隙。

首先考虑K闭合，即不考虑齿间侧隙的情况，设ωw为车轮角速度;θ为扭转角;TL为负载;i为减速比建立系统的扭转振动微分方程:

将式(6)改写为标准形式的状态空间方程，并进行拉普拉斯变换得到系统的传递函数矩阵，结合驱动系统的数学描述，可得电机转速ωm对电机转矩Tm的传递函数Gm(s)，如式(7):

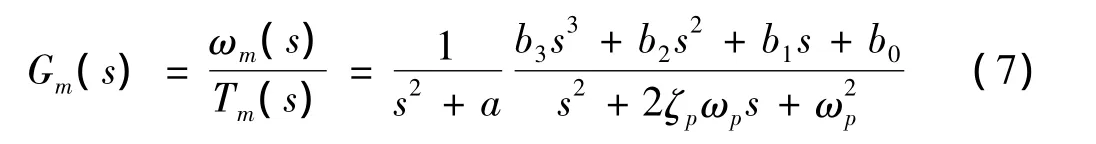
电机角加速度ωm对电机转矩Tm的传递函数如式(8)所示，其传递特性见图6。

图5 Gma(s)的频率特性Fig.5 Frequency characteristic of Gma(s)

可知，电机转速在50.9 rad/s附近存在共振，即8.1 Hz为此简化驱动系统的扭转振动固有频率。电动车在受到突变的转矩输入时，整车沿纵向产生8.1 Hz左右的明显波动，此为抖动控制的参考频率。

2.2 前馈控制器

控制系统由车辆控制器、扭转振动控制器和电机控制器三部分组成。车辆控制器根据驾驶员操作输入(加速踏板位置)和车辆状态(如车速)决定电机转矩信号值;前馈控制器用于调谐整车控制器的输出转矩，减小整个传动系统受到的冲击，并将协调后的控制信号传递给电机控制器;电机控制器按照新的指令计算电机工作电流和电压，输出转矩驱动车辆行驶。前馈控制器Gc(s)由参考模型的传递函数Gr(s)和实际模型的传递函数Gp(s)决定:

前馈控制器Gc(s)使得控制后的系统可以达到参考模型Gr(s)的响应特性，即以电机转速ωm为输出，电机转矩为输入的传递函数响应特性。

协调后的转矩与未施加前馈控制的原始转矩对比，如图6所示。从图中看出，变化后的转矩不再是理想的阶跃指令，而是一种矢量叠加的形式，其目标是使简化模型在冲击作用下响应幅值最小。

图6 电机转矩信号Fig.6 Motor torque signal

2.3 前馈控制的实车验证

前馈控制属于开环控制，只需要建立较为精确的简化模型，不需要检测电机或者车轮处的转速和角加速度等信号等进行反馈，对其进行控制效果的验证可以基于前述整车仿真平台，也可以直接在整车上进行验证。选择在整车上进行直接验证的方法，保证简化模型的准确性及控制效果的可行性，为后续反馈控制或者被动控制奠定基础。

图7 整车声振试验现场Fig.7 Vibration and noise test

在转鼓试验台进行瞬态工况(突加突减油门)下，无控制与前馈控制的对比试验，如图7所示。工况选取为突加至一定车速(20 km/h、40 km/h、50 km/h、60 km/h、80 km/h)然后突松油门。不同目标车速对应不同的油门开度，也就是对应不同的整车控制器指令转矩。记录驾驶员座椅底板处的三向加速度时域信号。以50 km/h瞬态工况为例，控制前后车身三向振动加速度信号如图8所示。

图8 振动加速度Fig.8 Acceleration of vibration

从图8(a)可以看出，控制前，在3 s处突加油门时，整车在突加转矩的冲击下产生明显的振动，幅值较大;在12 s处突松油门时也产生大幅值的冲击振动;20 s处的振动峰值对应能量回馈终止的转速设定点，对此点进行重新标定即可减小这一峰值。从图8(b)中可以看出，对应的瞬态工况下，峰值都有大幅度的降低。其余工况也取得了类似的效果，车身瞬态工况下的振动情况均得到改善，这与驾驶员的主观感受一致。

从时间历程图上，可以直观看到控制前后的效果，若要进一步对此进行量化，可用振动加速度加权加速度时间历程峰值、加权加速度均方根值、峰值系数和振动剂量VDV等指标来评判振动控制前后的效果，根据ISO2631－1:1997(E)标准规定，当振动波形峰值系数＜9时，用加权加速度均方根值来评价振动对人体舒适性和健康的影响。当峰值系数＞9时，用振动剂量来评价，处理结果如表1所示。

表1 前馈控制前后车身振动情况Tab.1 Body VDV before and after feed －forward control

可以看出，除个别数据外，前馈控制后相比于无控制，振动计量的结果都得到了一定程度的降低，表明车辆在进行前馈控制后振动舒适性有所提高。

3.4 后馈补偿器

前馈控制无法完全解决瞬态振动问题，因为简化模型的不确定性、传动系统间隙以及路面干扰等因素的存在，简化模型无法完全体现实际车辆的复杂情况。例如，在图4中考虑K存在的情况，即存在齿轮间隙的情况下(可视为干扰信号d)，则需要在前馈控制的基础上，进一步加入后馈环节，组成完整的扭转振动控制方案，其示意如图9所示。

图9 主动控制系统结构Fig.9 Active control system scheme

控制器由前述前馈控制器和反馈补偿器组成，各个参数间的传递关系如图10所示。

图10 主动控制传递关系Fig.10 Transfer relationship of active control

在反馈补偿器中，带通滤波器H(s)为:

其中:k=1－ζp，带通滤波器的中间频率为系统的固有频率ωp。假设电机的转矩信号，则系统电机转速响应ωm与扰动信号d的关系为:

可以看出传递函数中固有频率ωp的阻尼比为1，能很好地抑制阶跃输入下系统的振荡。验证前馈－反馈控制器对扰动的作用效果，在仿真模型中加入扰动转矩(0.2 s处施加－120 Nm到60 Nm的脉冲)，模拟齿侧间隙等因素引起的干扰对传动系统扭转振动的影响。脉冲转矩取值综合瞬态仿真激励、电机参数及实测峰值转矩给出，其依据有:① 电机峰值转矩为150 Nm，阶跃激励值在0～150 Nm之间;② 转鼓上进行实车试验测得的转矩范围在－30～130 Nm之间;③ 考虑齿侧间隙后的冲击激励幅值应大于不考虑侧隙时的峰值。不失一般性，取考虑侧隙与否的差值60 Nm，即电机峰值转矩和额定转矩的差值进行仿真分析。不考虑齿间侧隙时瞬态仿真给出的阶跃激励为0～120 Nm，考虑齿间侧隙时总的冲击应该为0～180 Nm。因此取齿间侧隙引起的脉冲转矩为－120 Nm～60 Nm叠加在初始转矩120 Nm上，最终可获得0～180 Nm的脉冲冲击效果。控制效果如图11所示。前馈控制和前馈－后馈的控制转矩如图11(a)所示，电机角速度和车轮角速度变化如图11(b)、(c)所示。

图11 主动控制效果Fig.11 Effect of active control

从控制的仿真结果看，反馈控制环节能够抑制扰动转矩引起的传动系统振动，弥补前馈环节无法抑制扰动转矩引起的传动系振动的不足。值得一提的是，反馈控制虽然在仿真层面取得较好的效果，但是要在整车试验验证层面取得理想的效果，其鲁棒性和稳定性还有待更深入的研究。

3 悬置系统被动优化

在前述主动控制的基础上，还可以通过优化悬置系统(传递路径2)，进一步减小电机动态造成的瞬态振动向驾乘人员的传递。选取悬置元件刚度和悬置点位置坐标作为优化变量，运用具有高效搜索能力的带惩罚函数的遗传算法对电机动力总成悬置系统进行优化。

3.1 悬置系统模型

电机动力总成悬置系统在质心坐标系OcXYZ下的拉格朗日方程表达式:

式中:ET、EV、ED为电机动力总成悬置系统振动动能、势能和耗散能;q为电机动力总成广义坐标，q=[x，y，z，θx，θy，θz];F为电机动力总成悬置系统的广义激励力。

悬置点动反力主要包括悬置点位移引起的弹簧力和速度引起的阻尼力，电机动力总成质心坐标系下第i(i=1～3)个悬置点的动反力:

式中:Ti为第i个悬置点坐标方向转移矩阵。

3.2 悬置系统优化

有别于传统内燃机，电机总成的瞬态冲击效应相对明显，悬置支撑处的动响应是较为重要的评价指标，选取悬置点各向动反力峰值最小为优化目标，对瞬态加速工况进行优化。采用线性加权的方式得到优化目标，总优化目标函数表示为:

式中:fix，fiy，fiz分别为第 i个悬置点的 x，y，z方向动反力峰值;ωix，ωiy，ωiz分别为 fix，fiy，fiz的加权系数，取某向动反力的峰值在各向动反力峰值之和中的占比作为该向动反力峰值的加权系数。

根据电机总成悬置系统的特点，对橡胶元件刚度，悬置点坐标以及电机总成关键位置位移振幅进行约束，具体约束情况如下。

(1)橡胶元件刚度:橡胶元件的刚度约束范围上下限分别定为4×106N/m和5×105N/m，且保证同一悬置的轴向刚度小于其径向刚度;

(2)悬置点坐标:将各悬置点位置坐标约束在各向距离的15 cm范围内;

(3)关键位置位移振幅:使电机总成质心最大振幅A(sc)≤5mm;

(4)解耦率:电机总成θy方向的振动能量分布占比Tpy≥90%。

考虑到优化问题包含多个约束条件，且存在非线性约束，将惩罚函数这一常用的处理约束条件的方法与遗传算法相结合，对电机总成悬置系统瞬态工况下的动反力峰值进行优化。

构造惩罚函数F'(x)，其一般形式如下:

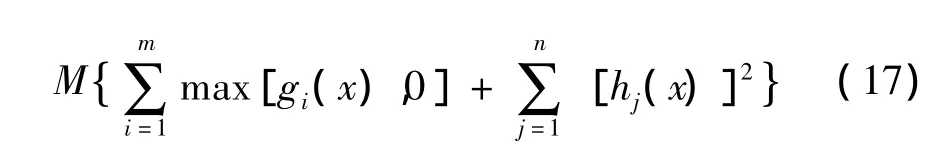
右边第二项为惩罚项，和约束条件有关，M为惩罚因子，一般取为较大的正数。当优化搜索脱离可行域时，F'(x，M)就会非常大，进而使得搜索优化回归到可行域内。结合MATLAB自带的遗传算法函数可以方便的对电机动力总成悬置系统进行优化，设置种群数目为500、交叉概率为0.8、最大迭代数为300，优化后的悬置点坐标值(略)和悬置元件刚度见表2。

中国的家训内容极其丰富，总的来讲不外家法和家礼。清代有一位学者说现在人们讲家法的多，而讲家礼的少。然后他做了比较，给出了法和礼的不同。他说法使人遵，有了这个法就要遵守这个法；礼使人化，春风化雨，润物无声。接着他又讲，法使人畏，礼使人亲。他的比较是有意义的。为什么中国文化强调礼乐教化，因为它是使人化、使人亲的。家训里需要有家法，但更需要有家礼。

表2 优化后悬置元件刚度值Tab.2 Stiffness of mounting after optimization

4 主动－被动一体化控制仿真平台验证

基于前述电动车多体动力学仿真模型，输入悬置被动控制后的坐标及刚度参数，并与单纯进行主动控制时的仿真结果进行对比。车身质心和动力总成质心三向加速度如图12所示。从图12(a)看出，相比于无控制，主动控制和主被动一体控制后车身纵向加速度波动明显得到改善，最大的第一波动峰值得到有效降低，0.7 s后的连续波动得到有效抑制，加速度达到稳态的时间也明显加快。主动控制与无控制时相比，车身纵向最大振动幅值降低到1.86 m/s2，降幅达到44.54%，车身横向振动也得到一定改善，降幅为34.1%;在进行悬置系统优化后，车身纵向和横向振动降幅进一步达到46%和70.5%。

同样可以查看动力总成质心沿水平、纵向及垂直方向的波动衰减效果，如图12(b)所示。主动控制对动力总成的纵向振动和横向振动有较大改善，振动幅值分别降低了51.42%和43.67%，进一步进行悬置系统优化后横向位移降低到52.26%。主动控制对车身纵向振动有明显的改善作用，对车身和动力总成的垂向振动无明显影响;相比于单纯的主动控制，主动－被动一体化控制可进一步减小车身纵向和横向以及动力总成质心Y方向的振动幅值，但对X向和Z向的加速度影响不大。

悬置系统三个悬置点的三向动反力结果如图13所示。主动控制后，三个悬置各向动反力峰值都得到一定的降低，其中悬置1的x向、y向和z向分别降低26.6%、15.69%和16.8%，悬置2 的 x 向和 z向动反力降幅较明显，分别降低27.3%和26.5%，y向略有降低，降幅为3.5%，悬置3的三向分别降低21.8%、16.8%和13.3%。悬置动反力峰值的降低能有效改善悬置元件的使用寿命。而进一步对悬置系统优化后，相比于单纯的主动控制，进一步降低了部分悬置的动反力峰值，特别是悬置3的Y向和Z向。主动－被动一体化控制在有效抑制车身质心和动力总成质心加速度抖动的同时，进一步降低了悬置的动反力峰值。

图12 振动加速度Fig.12 Acceleration of vibration

图13 悬置动反力Fig.13 Dynamic force of mounting system

5 结论

(1)结合电动车动力系统集成、常啮合及振动耦合的特点，考虑动力总成内部转子－齿轮系统的传动作用，搭建了电动车多体动力学的仿真平台，分析了抖动产生的机理、传递路径及贡献量，为抖动现象的控制提供了有效的仿真及验证平台。

(2)前馈控制可以有效的改善整车控制器的指令转矩，减小传动系统在冲击下的扭转振动，试验也取得较好的效果;反馈控制对突加扰动转矩具有较好的抑制作用，基于两者的主动控制器可以有效减小车身的纵向抖动。

(3)悬置系统优化可以有效减小动力总成悬置系统三个悬置点的动反力，降低动力总成振动向整车的传递。结合传动系统主动控制的悬置系统被动优化可以进一步改善电动车的瞬态振动性能，提高电动车的驾乘舒适性。

研究的不足:主动控制中的反馈控制，其鲁棒性和鲁棒稳定性有待进一步深入研究，以期在实车上获得较好的控制效果。

［1］于蓬，贺立钊，章桐，等.集中电机驱动车辆动力传动系统NVH性能研究现状与展望［J］.机械设计，2014，31(3):1－5.YU Peng， HE Li-zhao， ZHANG Tong，et al. NVH performance study of centralized motor drivenvehicle power train［J］.Journal of Machine Design，2014，31(3):1 －5.

［2］于蓬，章桐，郭荣.车辆传动系扭转振动主动控制研究现状及趋势［J］.机电一体化，2014，6:3－10.YU Peng，ZHANG Tong，GUO Rong.The current state and trends of automotive drive train torsional vibration active control［J］.Mechatronics，2014，6:3－10.

［3］Moriya K，Ito Y，Inaguma Y.Design of the surge control method for the electric vehicle powertrain［J］.SAE Technical Paper Series，2002－01－1935，2002.

［4］Amann N，Bocker J，Prenner F.Active damping of drive train oscillations for an electrically driven vehicle［J］.Mechatronics，IEEE/ASME Transactions on，2004，9(4):697－700.

［5］傅洪，田光宇，陈红旭，等.电机－变速器集成驱动系统扭振振动控制的研究［J］.汽车工程.2010，32(7):596－600.FU Hong，TIAN Guang-yu，CHEN Hong-xu，et al.Study on the torsional vibration control of motor transmission integrated drive system［J］.Automotive Engineering，2010，32(7):596－600.

［6］Karikomi T，Itou K，Okubo T，et al.Development of the shaking vibration control for electric vehicles［J］.SICE －ICASE International Joint Conference，2006:2434 －2439.

［7］蔡建江，左曙光，刘学明，等.燃料电池轿车驱动电机悬置的优化设计［J］.振动、测试与诊断，2008，28(1):5 －8.CAI Jian-jiang，ZUO Shu-guang，LIU Xue-ming，et al.Optimization design of fuelcellcar's driving motor mount［J］.Vibration，Measurement＆ Diagnosis，2008，28(1):5 －8.

［8］余卓平，王建，张立军，等.燃料电池轿车动力总成悬置系统的优化设计［J］.机械设计，2009，7:50－54.YU Zhuo-ping， WANG Jian， ZHANG Li-jun， et al.Optimization design on motivity assembly suspension system of fuel cell saloon car［J］.Mechanical Design，2009，7:50－54.

［9］敬辉.电动汽车驱动传动系统扭振控制与研究［D］.上海:同济大学，2012.

［10］贺立钊.考虑电机激励可控的动力总成悬置系统优化分析［D］.上海:同济大学，2014.