“三角形的中位线定理”练习课案例及反思
张华
练习内容:人教版八年级下册数学第49页练习。
课前组内口头复习了平行四边形的定义、性质及其判定。
师:我们上节课学习了三角形的中位线定理,其内容是什么?
生:三角形的中位线平行于第三边,并且等于第三边的一半。
师:下面我们做第49页练习1、2、3。请同学们先独立思考,完成。
练习:
1.如图1,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
2.如图2,直线l1∥l2,在l1,l2上分别截取AD,BC,使AD=BC,连接AB,CD,AB和CD有什么关系?为什么?
3.如图3,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点间的距离?根据是什么?
(学生独立思考8分钟)
师:请组内解疑。(组内解疑5分钟)
师:我们集体展示各组的答案及其思考过程。
组1:在图4中,我们组能画出5个平行四边形。(生边说边画)连接D、F,并延长DF至G,使FG等于DF,连接CG。
(话未说完)
生1:这样的平行四边形不符合题意,要以这些点为顶点的平行四边形才符合题意。如果这样画也不止5个,所以我们组能画出三个平行四边形。分别连接DE、EF、DF,则四边形ADEF、四边形BEFD、四边形CFDE都是平行四边形。
老师:同学们同意吗?
学生:同意!
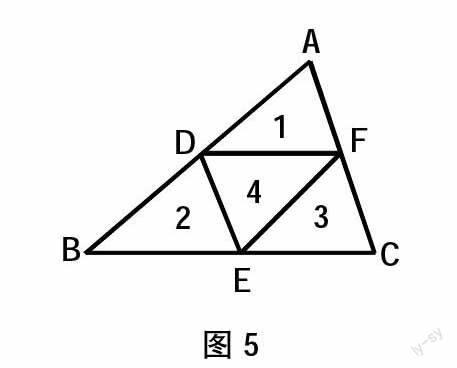
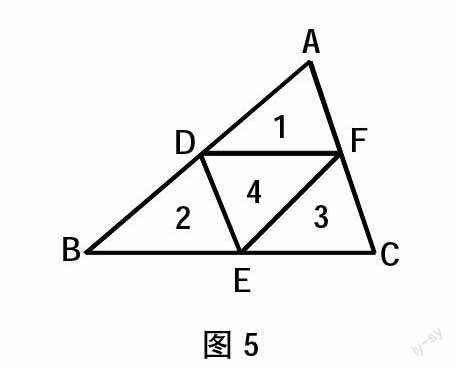
老师:如图5,大家看看这个三角形被中位线分成了几个三角形?这几个三角形是全等的吗?
陈××(年级前三学生,自言自语):4个,不全等,一定不全等。
(有的觉得全等,有的觉得不全等,感到茫然,总之不确定。)
教师:好,大家讨论一下。
(沸沸扬扬的一阵讨论后。)
生2:请看:此生将三角形ADF、三角形BDE、三角形CEF和三角形DEF分别标上1、2、3、4,因为1+4是平行四边形,2+4、3+4都是平行四边形,平行四边形的一条对角线把这个平行四边形分成两个全等的三角形,反过来,任意两个全等的三角形都可拼成一个平行四边形。1、2、3都和4全等,那么这四个三角形全等。
师:大家同意这个说法吗?
全班:同意!(陳××听到同学的讲解连连点头)
如图6,A′B′∥BA,B′C′∥CB,C′A′∥AC,∠ABC与∠B′有什么关系?线段AB′与线段AC′呢?为什么?
师:奖本组一分,好不好?这组同学真得很棒,下面请同学们打开第50页11题试试看。
(两分钟后)
组3:我们组可以利用平行线的性质和平行四边形的判定方法,发现这道题图中有三个平行四边形,由此可以得到线段和角相等。
组4:这道题和49页的练习1是逆向思维,换了一种眼光看问题,其认识事物的本质是一样的。
师:哇!的确如此,本组同学慧眼识珠,很会学习,是我们的表率。下面请各组的4号到小黑板上展示练习2。
(通过练习2,目的让学生复习一组对边平行且相等的四边形是平行四边形的判定方法,再根据平行四边形的性质得到AB与CD平行且相等。)
师:各组到自己的小黑板上展示第三题。
(每一组都在自己的小黑板上刷刷作图,几分钟后。)
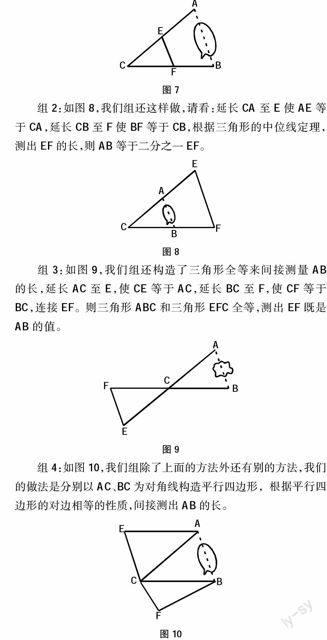
组1:如图7,我们组连接AC、BD的中点E、F,根据三角形的中位线定理,测出EF的长,则AB等于2倍的EF。
组2:如图8,我们组还这样做,请看:延长CA至E使AE等于CA,延长CB至F使BF等于CB,根据三角形的中位线定理,测出EF的长,则AB等于二分之一EF。
组3:如图9,我们组还构造了三角形全等来间接测量AB的长,延长AC至E,使CE等于AC,延长BC至F,使CF等于BC,连接EF。则三角形ABC和三角形EFC全等,测出EF既是AB的值。
组4:如图10,我们组除了上面的方法外还有别的方法,我们的做法是分别以AC、BC为对角线构造平行四边形,根据平行四边形的对边相等的性质,间接测出AB的长。
师:同学们,你们认为以上的方法都可行吗?
生:可行!
师:我为同学们有这么多的测量方法感到由衷的高兴,同学们已经具备一定的解决问题的方法与策略,以上各组都给一分的奖励,大家觉得哪一组应多奖励一分?
生:(异口同声)第四组。
师:我也这么认为,好!大家想想,这些方法中,哪些方法比较简单些?
(各抒己见。有的说应用三角形的中位线定理,有的说都还比较简单。)
师:在纸上做的话都比较简单。
生:(迫不及待)我们在解决实际问题的时候除了考虑方法外,还要考虑方法的便捷性和可行性。我们觉得还是应用三角形中位线定理方便。
(全班鼓掌)
(此时下课铃响了。)
师:同学们,本节课的内容就练到这里,最后请同学们畅所欲言:
1.对自己说我有哪些收获?
2.对同学有哪些温馨提示?
3.对老师说你还有哪些困惑?
教学后记:
1.本课经历了——自主学习、交流展示、反馈提高,即三环;以学生为主体、教师为主导、训练为主线,即三主。过程中有放手、有示弱、有利用,体现出了教师的智慧。
2.本节课在相信学生的基础上解放了学生被动的学习,利用学生互相间的促进给了学生充分展示的机会,发展了学生的表达自己见解能力。体现了:兴趣、知识、能力的课堂六字目标。
3.本节课充分发挥了小组合作学习,我认为自学给了学生“足够”的时间,展示给了学生“充分”的平台,点评给了学生“到位”的思维引领。
4.课堂中的评价不是为了评价而评价,而是自然地、自发地,呈现出和谐性、互助性、鼓励性、进取性。
有什么样的思想,就有什么样的行为,本节课是在我校推行打造“三环、三主、高效课堂”的教改环境中孕生的。上了这节课,使我更坚定一种教学理念:生本理念!进一步领悟到:课堂破局的真正奥秘在于“会学”,只有会学才能减少对“教师”的依赖。唯有敢于把学习还给学生,让学生去“经历”并且“经验”,学习的过程才充满律动。
我将紧跟教改步伐,在教研组释放正能量,让姚坪中学的数学课堂从此充满生命的活力,让学生在数学学习的过程中痛并快乐着!
?誗编辑 温雪莲

