MATLAB/SIMULINK仿真技术在研究生《线性系统理论》课程教学中的应用

周颖

摘 要：《线性系统理论》是控制科学与工程学科硕士研究生的重要基础课程之一。目前多采用“课堂讲授”辅以少量试验的传统教学方式，学生较难理解，教学效果差强人意。该文将MATLAB/SIMULINK引入到研究生《线性系统理论》课程的教学过程中，克服了传统教学方式存在的缺陷。不仅有助于加深学生对所学内容的理解和掌握，而且在培养学生分析、解决问题以及提高科研能力等方面有着积极的促进作用，取得了令人满意的效果。

关键词：线性系统理论 研究生课程教学 MATLAB/SIMULINK

中图分类号：TP13 文献标识码：A 文章编号：1674-098X（2015）04（c）-0081-02

《线性系统理论》是现代控制理论体系中最基本的分支，是控制理论与控制工程、系统工程等多个学科的硕士研究生学位课程。该课程与实际工程应用联系紧密，在整个专业知识体系中占据非常重要的地位。该课程属于原理性课程，涵盖了自动控制学科的一些最基本的理论、方法和知识点。现在该课程的教学通常采用传统的“课堂讲授”再辅以少量试验手段来进行，存在如下问题：因为该课程理论性强，较为抽象，单纯的课堂教学较为枯燥；同时试验依赖于客观条件，试验结果有时并不理想，起不到应有的辅助理解作用。上述原因，使得传统教学方法的教学效果不够理想。如何在课程教学中，使学生在学习线性系统理论基本内容时，能更深刻地领会和掌握理论本质，是课程教学过程中面临的难题。

MATLAB/SIMULINK具有功能丰富的应用工具箱，为用户提供了大量方便实用的处理工具，深受工程技术人员及科技专家的欢迎，目前已成为科学分析和计算领域的主流软件。对于控制科学与工程等相关工科专业来讲，MATLAB/SIMULINK的控制系统工具箱含有丰富的线性连续系统时域分析功能，编程简洁、仿真效果非常直观。我们将充分利用MATLAB/SIMULINK的上述优点，将其应用于《线性系统理论》的教学，来克服传统教学方式的缺陷，使学生可以直观理解课程内容的重点，掌握分析问题的方法，同时对学生科学研究能力的培养也具有积极作用。

1 MATLAB/SIMULINK在《线性系统理论》教学中的应用例

系统的状态观测问题是线性系统理论中一个重要问题，需要根据响应曲线来分析观测器性能，而上述图形均需要复杂的计算过程，常常花费大量的时间，并且效果并不直接。为此，可以利用MATLAB/SIMULINK提供的M-函数程序包，可以很方便地调节各种控制参数，使学生直观了解设计参数变化对控制系统动态特性的影响。这解决了传统理论教学中教师板书画图耗费时间及不准确的弊端，有利于学生对抽象理论的理解，极大地提高了课堂效率。

下面，通过一个具体实例来说明MATLAB/SIMULINK在线性系统理论教学中的应用。

例1.状态观测问题是线性系统理论中的一个难点，需要学生了解其内在的原理，明白观测器参数在其中所起得作用。通过一个例子对MATLAB/SIMULINK的应用做进一步阐述。

取矩阵，，系统的初始状态分别取为，观测器的初始状态取为。

對此问题，可以利用MATLAB/SIMULINK的M-函数来求解，首先建立原系统与观测器的微分方程组如下：

function xdot=DxDt（t，x）

xdot=[x（2）；...

1.08*（1-0.95*x（2））-0.81*x（1）+sin

（t）；...

x（4）+10*（x（1）-x（3））+0.36*（3-0.95

*x（2））；...

1.08*（1-0.95*x（3））+sin（t）-0.81*x（1）+0.81*x（3）]；

然后调用上述程序：

tspan=[0，2]；

x0=[0；1；0；0；0.02]；

[tt，xx]=ode45（@DxDt，tspan，x0）；

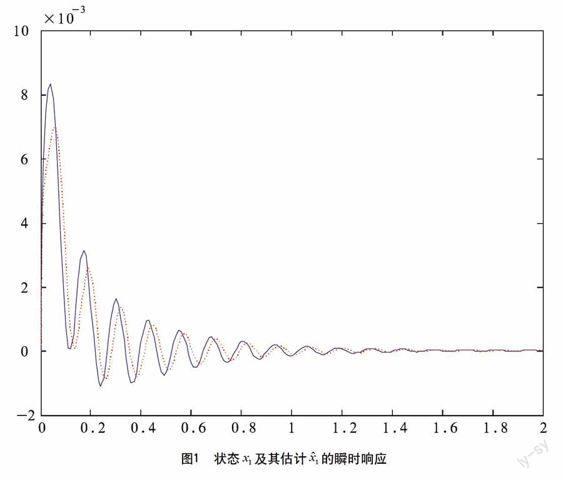
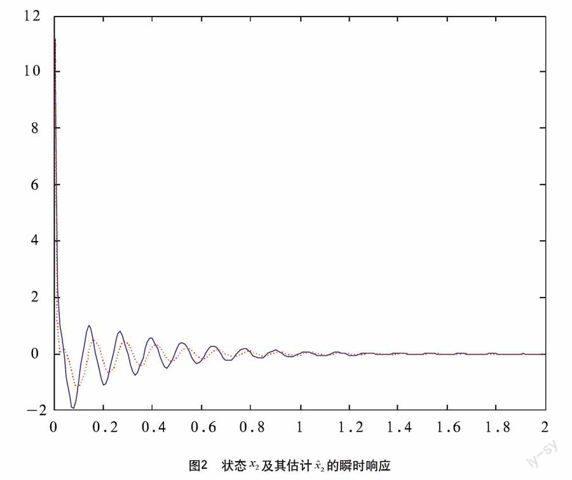
再利用MATLAB的PLOT命令绘出观测误差曲线图形。原系统状态及观测状态分别如图1、图2所示，其中实线为原系统状态，虚线为观测状态。

显然，观测器的观测效果非常直观的体现在了仿真图形中，学生还可以根据需要，在程序中调节观测器的参数设置，观察不同参数设置下的系统瞬时响应。

2 结语

MATLAB/SIMULINK的引入，使《线性系统理论》的教学由原来枯燥的纯原理性“静态”教学，转变为形象生动的、与工程实际紧密结合的“动态”教学。通过这种途径，使学生能直观地领会和理解分析方法和处理结果。另外，MATLAB/SIMULINK的引入还可以帮助学生熟练掌握该软件，并将其应用于解决控制系统的分析和设计问题，对学生科学研究能力的培养也有很大的促进作用。

参考文献

[1] 刘永强，董翠敏.浅谈《自动控制原理》课程教学改革[J].湖南农机，2008（1）：83-85.

[2] 郑大忠.线性系统理论[M].2版.北京：清华大学出版社，2007.

[3] 张志涌.精通MATLAB6[M].5版.北京：北京航空航天大学出版社，2003.

[4] 孟月波，嵇启春.线性系统理论本科教学改革与实践教学[J]，电气电子教学学报（增刊），2009（31）：23-25.