一种基于嵌入式平台的机械臂体感控制系统

周海芳， 查帅荣， 章 杰， 陈志聪

(福州大学 物理与信息工程学院， 微纳器件与太阳能电池研究所, 福建 福州 350116)

一种基于嵌入式平台的机械臂体感控制系统

周海芳， 查帅荣， 章 杰， 陈志聪

(福州大学 物理与信息工程学院， 微纳器件与太阳能电池研究所, 福建 福州 350116)

针对传统机械臂控制方式复杂且效率低的问题， 研制了一套惯性式动作捕捉的体感控制系统. 该系统在用户手臂绑定多个节点， 每个节点由加速度传感器、 陀螺仪和磁通传感器组成. 节点采集手臂运动数据发送到嵌入式系统， 经过融合计算得到手臂运动状态， 并最终得出机械臂舵机转动角度. 在保证机械臂控制精度的前提下， 针对嵌入式系统硬件条件采用了降低系统延迟的分状态数据融合方案. 本系统在嵌入式平台上实现， 降低了动作捕捉成本， 提高了可移植性. 测试结果表明， 使用惯性式动作捕捉的机械臂体感控制系统动作响应延迟时间短、 机械臂动作较平稳.

体感控制； 嵌入式系统； 机械臂； 惯性传感器

0 引言

机械臂作为一种实用的机械设备， 频繁出现在日常生活和各种工业应用中. 但传统的机械臂控制方式效率低， 难以满足当今快节奏的生产和生活需求. 体感技术作为一种自然高效的人机交互方式[1]， 为机械臂控制提供了一条新的便捷途径. 目前的体感技术主要分为光学式和惯性式动作捕捉两类. 光学式动作捕捉精度高[2-3]， 但其具有成本高昂、 受场地限制等缺点. 而惯性式动作捕捉恰好能弥补以上不足， 近年来逐渐成为研究的热点[4]. 早期的惯性式动作捕捉主要采用加速度传感器采集人体动作数据[5-6]， 但是单一的加速度传感器数据无法保证高精度， 而且动作识别过程需要庞大的数据库支持. MEMS工艺的发展和高精度三轴陀螺仪的出现使得惯性式动作捕捉有了更多的可选方案[7-8]. Bengt等[9]利用陀螺仪和加速度传感器设计了4种不同的惯性传感器组合方案， 并从多方面对其进行了比较. Mohamed[10]设计了一种采用陀螺仪、 加速度传感器和磁通传感器检测病人关节状况的检测系统. 利用多传感器融合可以有效弥补单个传感器的不足， 但也增大了数据融合的难度和运算成本， 使得数据处理依赖于计算机端， 成本高， 不便于移植.

本研究针对多传感器数据融合成本高且不便于移植等问题， 在嵌入式平台上设计了三自由度机械臂体感控制系统. 该系统针对手臂不同运动状态读取相应传感器数据， 并根据机械臂控制需要采用分状态的数据融合方案， 旨在嵌入式系统中实现快速响应的体感控制.

1 系统概述

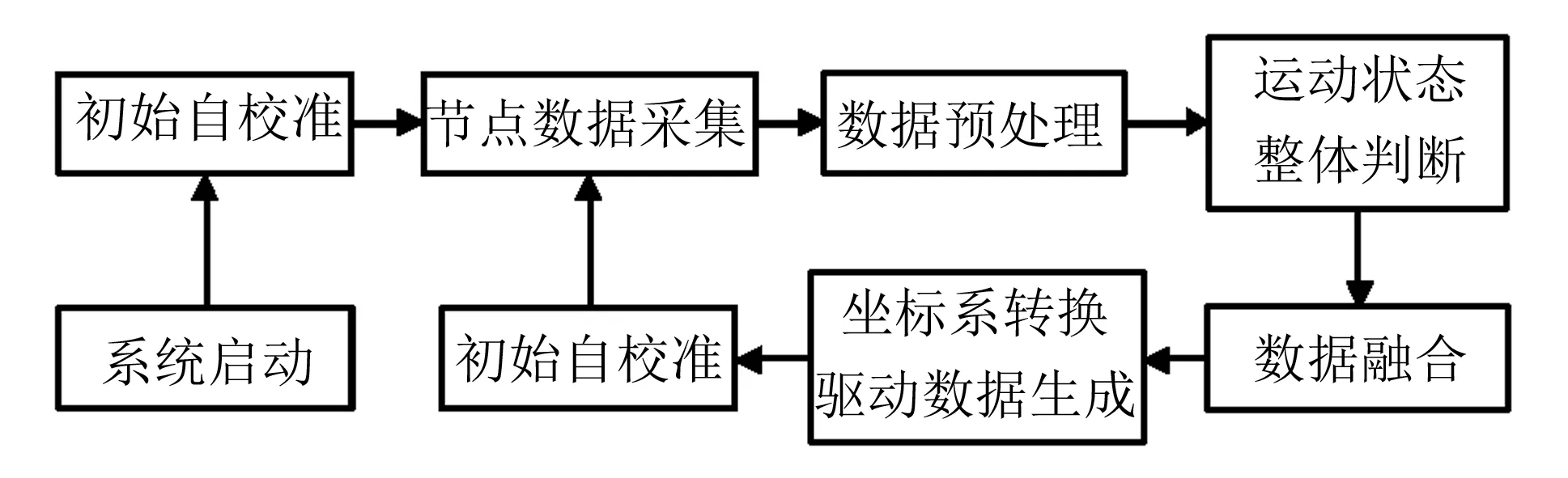
图1 系统结构示意图Fig.1 System block diagram

系统硬件部分由嵌入式处理器、 常用三自由度机械臂、 传感器固定手套和九轴惯性传感器模块(包含陀螺仪、 加速度传感器和磁通传感器)组成. 软件部分包含传感器初始姿态校准、 数据预处理、 单个节点姿态融合、 多节点相对姿态融合和舵机驱动数据生成， 系统整体结构如图1所示.

用户将惯性传感器模块和数据线固定在传感手套上， 经过一段时间的静态自校准得出初始漂移数据后开始运动手臂. 传感器模块将采集到的角速度、 加速度和磁通信号传递到嵌入式处理器. 嵌入式处理器先对采集的数据进行静态漂移校准和随机噪声滤波， 接着进行综合运动状态判断， 并根据不同的运动状态采用不同的数据融合策略. 通过对单个节点的数据融合得出该关节的运动姿态四元数(Q=v+xi+yj+zk)， 将不同节点的四元数进行比较和运算可以得出关节间的相对运动数据. 利用四元数和欧拉角的转换可以很方便地求出舵机控制数据， 进行范围限定和坐标系转换后用于舵机控制.

2 数据融合

由于传感器自身的制造工艺问题和环境的干扰[11]. 磁通传感器所采集到的数据具有显著非线性的特点[12]， 陀螺仪采集到的角速度的静态漂移误差在数据融合时经积分运算会积累增大， 加速度传感器采集到的数据常会出现不连续的尖峰， 使得机械臂控制过程中出现剧烈抖动. 根据不同传感器数据噪声的特点作相应的预处理， 将误差减小到一定范围内后方能用于后期数据融合.

2.1 运动状态划分

传感器模块可采集到固接于传感器坐标系的角速度向量ω， 加速度向量a和磁通向量Φ， 当手臂静止时， 加速度传感器所采集到的即为重力加速度. 通过对不同传感器数据的组合利用, 可以设计出多种数据融合方案， 不同的方案其精度、 延迟和对硬件的要求均有所差异. 重力加速度和地磁通量数据融合过程中无需经过积分运算， 漂移误差不会积累， 在长时间的使用中具有较好的稳定性. 但其相对于角速度数据融合运算复杂, 且容易受到运动加速度和外界磁场的干扰. 角速度数据受到的外界干扰较少, 且融合算法简单, 但在融合过程中漂移误差会随着积分运算会逐渐累积. 以往动作捕捉多采用计算机进行数据融合， 其优点是可将三类数据同时处理, 且动作响应延迟时间短， 但也增加了动作捕捉的成本. 综合考虑3个传感器的特点， 为降低系统成本， 提出一种分状态的融合方案. 数据融合整体流程如图2所示.

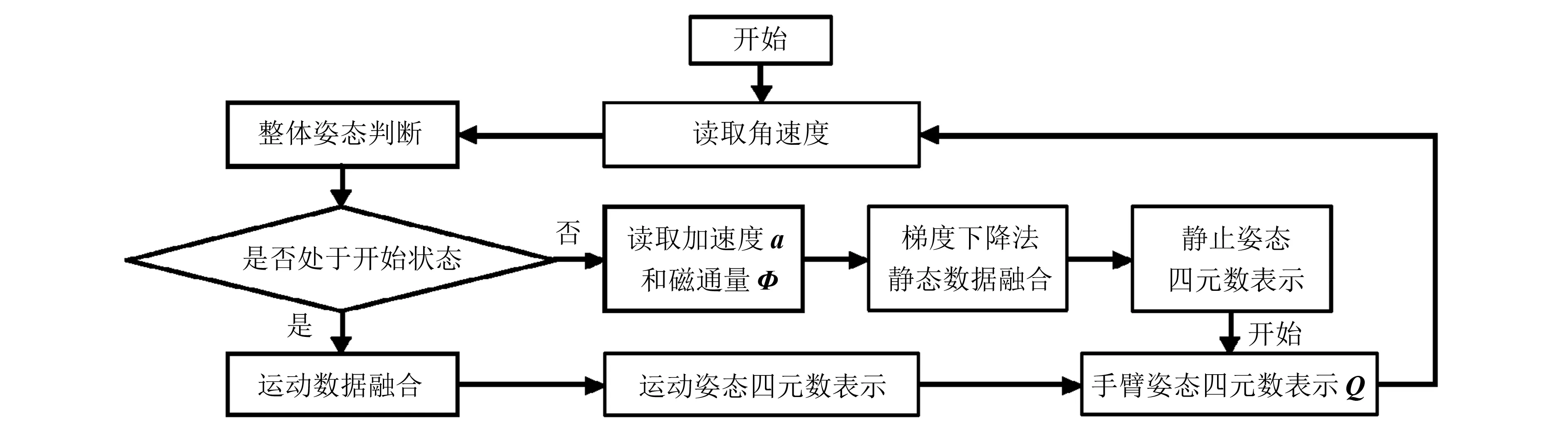
图2 数据融合流程示意图Fig.2 Flowchart of the data aggregation

首先为三轴角速度的平均值设定一个阈值， 当平均值高于阈值时就认为相应的手臂部位处于运动状态， 此时采用角速度进行动作数据融合； 否则处于静止状态， 此时选用加速度和磁通数据进行静态数据融合， 并用融合所得的结果校准手臂姿态. 此融合方案充分利用了三种数据的各自优点， 既能在运动中充分利用硬件资源实现低延迟的捕捉， 又可在静止时使用已空闲的计算资源进行自校准， 能够满足长时间使用的要求. 此外， 加速度数据仅在静止状态下使用， 避免了运动加速度对重力加速度所造成的干扰.

2.2 融合算法实现

当三轴角速度平均值高于设定的阈值时， 读取角速度数据进行动作数据融合. 陀螺仪采集到的角速度为传感器节点坐标系下的角速度ωs=ωxi+ωyj+ωzk， 融合的时间间隔为Δt. 通过角速度数据融合得到表示手臂姿态的四元数Q[13]， 其递推公式为：

其中:Qn与Qn-1为本次和前次融合所得的运动姿态四元数表示.

当三轴角速度平均值低于设定值时， 读取加速度数据和磁通数据进行静止校准. 利用传感器节点坐标系下的重力加速度和地磁通量大小不变而方向会随着传感器姿态变化的特性， 可以求出各传感器节点的姿态. 使用梯度下降法进行融合， 设加速度和地磁通量大小的误差函数分别为eg与eΦ， 定义合成误差函数e并计算其梯度：

▽

综上可得重力加速度和磁通融合递推公式：

Qn=Qn-1-S·▽

其中：Qn和Qn-1分别为本次和前次融合所得的静止姿态四元数表示；S为步长， 步长过小则融合速度慢， 步长过长会产生抖动.

3 机械臂控制数据生成

常用的机械臂逆运动学解法只考虑机械臂末端执行器的位置， 无法充分利用动作捕捉所获得的人体运动数据， 使得机械臂和人体手臂动作不能同步[14]. 为此， 针对人体手臂和机械臂两者运动模型的联系, 提出一种广义球坐标系， 将人体手臂姿态和机械臂姿态分别在标准球坐标和广义球坐标中表示， 通过坐标系转换, 产生便于机械臂控制的数据. 传感器采集的数据经过融合后, 可将上臂和小臂相对于地理坐标系的运动姿态分别用四元数Qu和Qf表示， 小臂相对于上臂的运动状态四元数Quf可表示为：

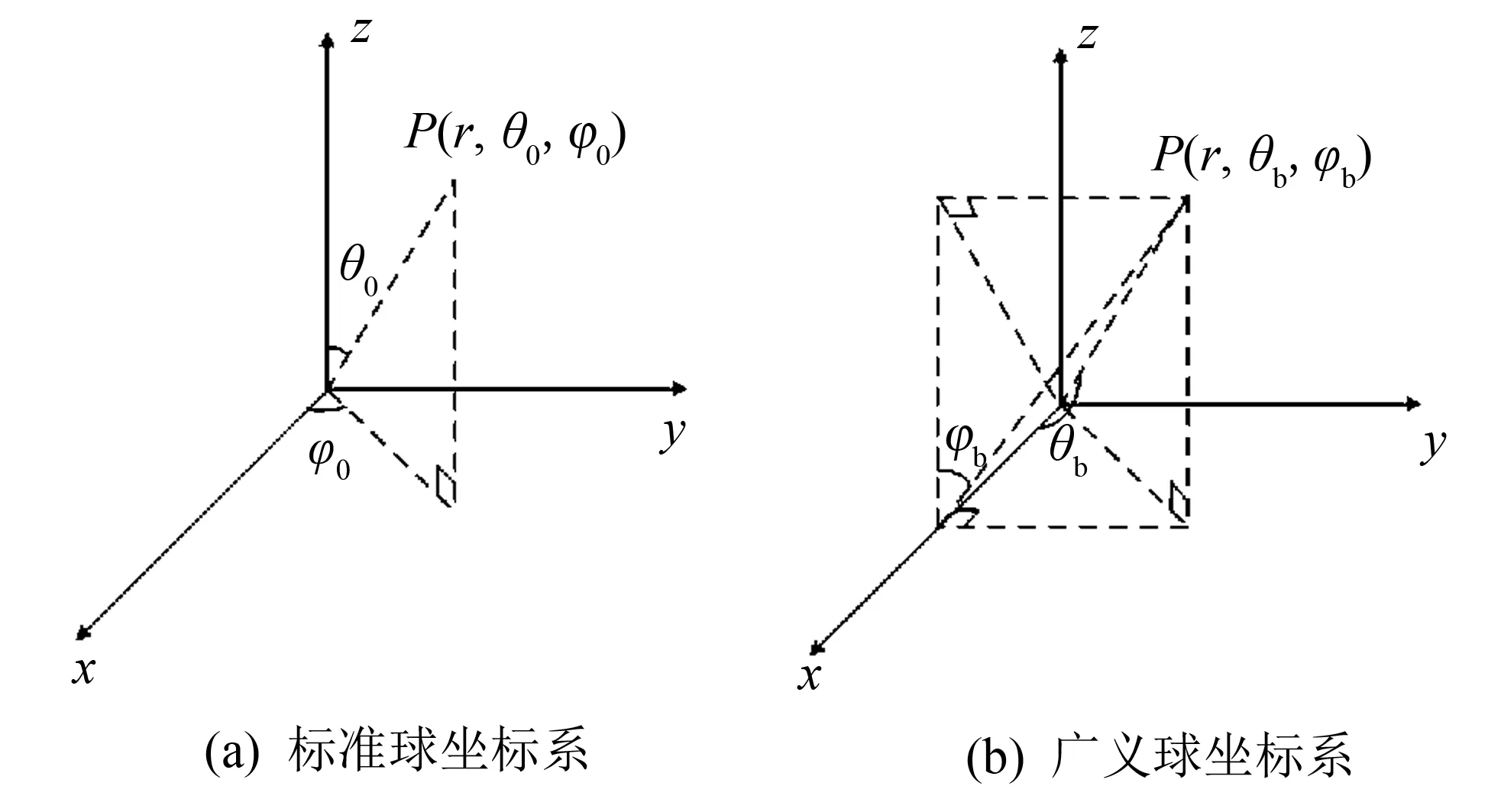
图3 标准球坐标和广义球坐标Fig.3 Standard spherical coordinate and generalized spherical coordinate

将四元数转换为相应欧拉角， 其对应的偏航角、 倾斜角和翻滚角分别记为φ、θ和ψ. 上臂处传感器节点的运动翻滚角是由于肌肉扭曲造成的， 因此仅考虑偏航角和倾斜角. 通过φu和θu可以将上臂的运动在一个标准的球坐标系O(r,θ0,φ0)中表示出来. 针对机械臂运动模型, 建立形如图3的扩展球坐标系B(r,θb,φb)， 作如下约定： 当z>0时， 90°>θb>0； 当z<0时， 0>θb>-90°； 当z×y>0时， 90°>φb>0； 当z×y<0时， 0>φb>-90°. 其中，θb和φb分别对应机械臂上臂关节处的两个舵机的转动角度.

将上臂运动数据从标准球坐标转换到广义球坐标中， 公式如下：

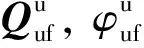
4 系统实现与结果分析

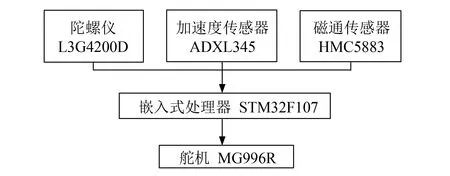
图4 系统硬件结构图Fig.4 The hardware structure of system

设计的机械臂体感控制系统硬件由惯性传感器节点(包含陀螺仪、 加速度传感器和磁通传感器)、 嵌入式处理器STM32F107和三自由度机械臂模型组成， 其硬件结构示意图如图4所示. 其中： 陀螺仪采用L3G4200D三轴陀螺仪， 随温度的漂移误差为0.03 dps·℃-1； 加速度传感器采用ADXL345三轴加速度传感器， 其漂移误差范围为-0.343～0.343 N·kg-1， 随机误差范围为-1.47～1.47 N·kg-1， 软件采用C语言在Keil 4.10平台上开发， 将相应的四元数运算和数据融合算法编写成通用的函数库， 便于移植和其他动作捕捉应用的开发.

4.1 静止校准步长分析

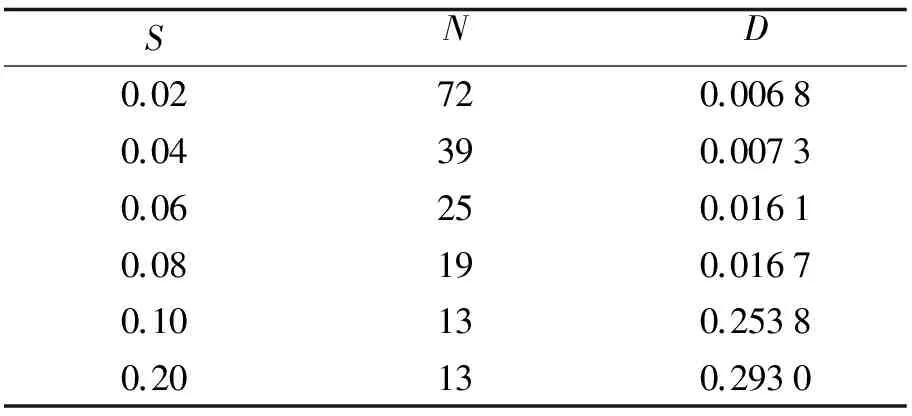
表1 步长与递推次数和旋转角度方差的关系

Tab.1 Relation between step, recursive number

在实际测试时， 手臂从运动到静止状态变化过程中机械臂会出现剧烈抖动， 对算法分析后得知， 该情况是由于梯度下降法收敛速度过慢造成的. 调节梯度下降法步长时发现， 如果其值过小， 会使得机械臂从运动到静止的瞬间出现剧烈抖动； 而步长值过大则导致手臂在目标位置附近反复地抖动. 因此， 选择合适的梯度下降法步长非常重要. 为此, 对梯度下降法步长S作了测试分析， 表1中显示了步长S、 融合递推次数N和稳定时四元数旋转角度方差D之间的关系. 从表中可以发现， 当步长S从0.02增大到0.2时， 所需的融合次数逐渐减少， 但稳定时D会逐渐增大. 步长超过0.1后对递推次数影响不大， 而方差却大幅增长. 因此， 综合考虑步长选择为0.08. 测试时， 手臂从运动到静止的过程中机械臂仅出现短暂的轻微抖动， 且稳定后无反复抖动现象， 基本满足机械臂控制的需要.

4.2 动作响应延迟时间测试

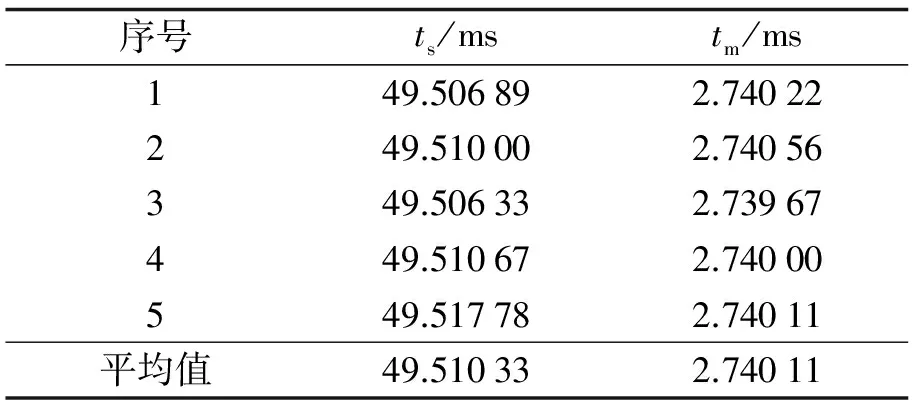
表2 分状态与多传感器同时融合延迟对比

注：tm为分状态融合的延迟时间，ts为多传感器同时融合的 延迟时间

机械臂的动作响应延迟时间由数据采集时间、 数据融合时间和舵机驱动时间组成. 其中， 数据采集和舵机驱动时间较短且基本固定， 因此， 动作响应延迟时间主要由数据融合时间决定. 分状态与多传感器同时融合方案延迟时间测试对比如表2所示. 从表2可知， 采用分状态融合方案动作响应时间降低了一个数量级. 测试时， 多传感器同时融合方案会让使用者有明显的延迟感觉， 而分状态的融合方案能快速响应.

图5为体感控制机械臂动作的截图， 从图中可看出手臂动作和机械臂动作基本一致， 各个关节多次测试的平均误差为2.3°， 能够反映使用者的动作意图. 本系统可以用机械臂模拟人体手臂的三自由度相关动作， 实现日常生活中机械臂的基本功能.

图5 系统体感控制测试图Fig.5 Intergration testing for the motion sensing control system

5 结语

设计了由惯性传感器节点、 三自由度机械臂模型与嵌入式处理器组成的体感控制系统. 采用基于运动状态判断的分状态数据融合算法避免了运动加速度对重力加速度的干扰， 减少了数据融合时间. 通过标准球坐标和广义球坐标的转换， 将人体手臂运动数据快速转化成机械臂控制数据， 实现了低延迟体感控制. 测试结果表明， 采用分状态融合方案机械臂动作响应延迟时间短， 机械臂动作较平稳， 实现了三自由度机械臂的体感控制. 数据的处理与控制均在嵌入式处理器中实现. 因此， 该系统具有低成本、 易拓展且便于移植等特点. 目前五个自由度机械臂的体感控制在进一步研究中.

[1] 席旭刚, 李仲宁, 罗志增. 基于相关性分析和支持向量机的手部肌电信号动作识别[J]. 电子与信息学报, 2008, 30(10): 2 315-2 319.

[2] Li J, Wan C K, Zhang D Y,etal. Markerless human motion capture by Markov random field and dynamic graph cuts with color constraints[J]. Science in China Series F: Information Sciences, 2009, 52(2): 252-259.

[3] Moeslund T B, Hilton A, Krüger V. A survey of advances in vision-based human motion capture and analysis[J]. Computer Vision and Image Understanding, 2006, 104(2): 90-126.

[4] 肖玲, 李仁发, 罗娟. 体域网中一种基于压缩感知的人体动作识别方法[J]. 电子与信息学报, 2013, 35(1): 119-125.

[5] Mantyjarvi J, Himberg J, Seppanen T. Recognizing human motion with multiple acceleration sensors[C]//IEEE International Conference on Systems, Man, and Cybernetics. Tucson: [s.n.], 2001: 747-752.

[6] Slyper R, Hodgins J K. Action capture with accelerometers[C]//ACM SIGGRAPH: Eurographics Symposium on Computer Animation. Aire-la-ville: [s.n.], 2008: 193-199.

[7] Cheng P, Oelmann B. Joint-angle measurement using accelerometers and gyroscopes: a survey[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(2): 404-414.

[8] 李启雷, 金文光, 耿卫东. 基于无线惯性传感器的人体动作捕获方法[J]. 浙江大学学报: 工学版, 2012, 46(2): 280-285.

[9] Kan Y C, Chen C K. A wearable inertial sensor node for body motion analysis[J]. IEEE Sensors Journal, 2012, 12(3): 651-657.

[10] To G, Mahfouz M R. Design of wireless inertial trackers for human joint motion analysis[C]//IEEE Topical Conference on Biomedical Wireless Technologies, Networks, and Sensing Systems (BioWireleSS). Santa Clara: [s.n.], 2012: 49-52.

[11] Dong W, Lim K Y, Goh Y K,etal. A low-cost motion tracker and its error analysis[C]//IEEE International Conference on Robotics and Automation. Pasadena: [s.n.], 2008: 311-316.

[12] 刘艳霞, 李希胜, 冯毅博, 等. 三轴磁罗盘标定位置分布的研究[J]. 仪器仪表学报, 2013, 34(3): 684-690.

[13] Sabatini A M. Quaternion based attitude estimation algorithm applied to signals from body-mounted gyroscopes[J]. Electronics Letters, 2004, 40(10): 584-586.

[14] 刘亚军， 黄田. 6R操作臂逆运动学分析与轨迹规划[J]. 机械工程学报, 2012, 48(3): 9-15.

(责任编辑： 沈芸)

A mechanical arm motion sensing control system based on the embedded system

ZHOU Haifang, ZHA Shuairong, ZHANG Jie, CHEN Zhicong

(Institute of Micro-Nano Devices and Solar Cells, College of Physics and Information Engineering,Fuzhou University, Fuzhou, Fujian 350116, China)

The traditional mechanical arm control is complex and inefficiency, so a mechanical arm control system for human motion capture using inertial sensor is designed and implemented in this paper. The system uses sensor nodes, which contain accelerometer, gyroscope and magnetic sensor, to collect motion data of the arms and transmit to the embedded system. Through data aggregation, the quaternion which expresses the moving state of arm is calculated and finally the angle of mechanical arm’s steering engines is obtained. Under the premise of ensuring the accuracy of mechanical arm, a data integration program of the different state is designed to reduce delay time for the embedded system, the system is implemented in an embedded system with low cost and portability. The experimental results show that the operating lag of system is short and the movement of mechanical arm is steady.

motion sensing control; embedded system; mechanical arm; inertial sensor

10.7631/issn.1000-2243.2015.04.0471

1000-2243(2015)04-0471-05

2014-08-28

周海芳(1972-)， 硕导， 副教授， 主要从事微纳材料与器件、 控制系统研究， zhhafa@163.com

国家自然科学基金资助项目(61006003)

TP241.2

A