用滴定突跃的绝对值推导四大滴定分析的直接准确滴定条件

乔成立

(齐齐哈尔大学应用技术学院　黑龙江齐齐哈尔 161006)

用滴定突跃的绝对值推导四大滴定分析的直接准确滴定条件

乔成立

(齐齐哈尔大学应用技术学院黑龙江齐齐哈尔 161006)

摘要建立了四大滴定分析“滴定突跃绝对值”的概念；用滴定突跃绝对值推导出四大滴定分析直接准确滴定的条件。

关键词滴定曲线方程滴定突跃绝对值视觉误差

Obtaining the Criteria for Direct Volumetric Titration

from the Absolute Value of Titration Jump

Qiao Chengli

(SchoolofAppliedTechnology,QiqiharUniversity,Qiqihar161006,Heilongjiang,China)

AbstractIn this paper, the absolute value of titration jump has been introduced and used to deduce the criteria for direct volumetric titration.

Key WordsTitration curve equation; Absolute value of titration jump; Visual error

直接准确滴定的条件是滴定分析理论的重要环节，无论是设计一个新方案，还是解决一个实际问题，都要首先考虑是否能直接准确滴定。在教学中，直接准确滴定的条件也是教学重点和难点；因此，如何处理直接准确滴定的条件是每一位从事分析化学教学的教师都应认真思考的问题。文献[1-3]都用林邦终点误差公式对此进行处理。如文献[1]推导配位滴定直接准确滴定的条件如下：

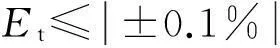
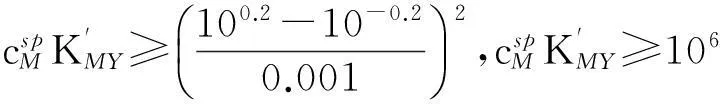
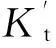
其次，文献[1-3]没有推导氧化还原滴定和沉淀滴定分析直接准确滴定的条件，这在知识结构的完整性上是个缺憾。

基于以上原因，笔者用林邦滴定曲线方程建立了“滴定突跃绝对值”的概念，并用滴定突跃绝对值推导出四大滴定分析直接准确滴定的条件。这样就弥补了用林邦终点误差公式推导直接准确滴定的条件在教学效果上的不足；同时，也为用林邦滴定曲线方程研究滴定分析的理论做了一些尝试。

1配位滴定

1.1　配位滴定突跃绝对值的建立

配位滴定突跃绝对值是滴定曲线突跃在纵坐标 (纵坐标是被滴定离子M的浓度的负对数pM，横坐标是滴定分数a)方向上的大小。因为配位滴定分析要求的准确度是0.1%[1-3]，所以配位滴定突跃绝对值可定义为化学计量点的pMsp与化学计量点前0.1%的pMep之差的2倍。若设滴定突跃绝对值为ΔpMt，则其等于滴定分数a=1与a=0.999时pM之差的2倍。即：

ΔpMt=2(pMsp-pMep)

(1)

由文献[1-6]可知，若用Kt表示滴定反应的稳定常数，则配位滴定的林邦滴定曲线方程为：

Kt[M]2+(cMKt(a-1)+1)[M]-cM=0

当a=1时，林邦滴定曲线方程变为：

Kt[M]2+[M]-cM=0

解得：

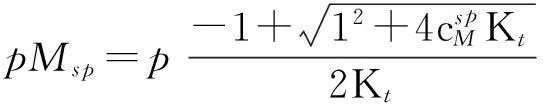
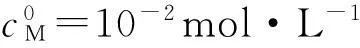
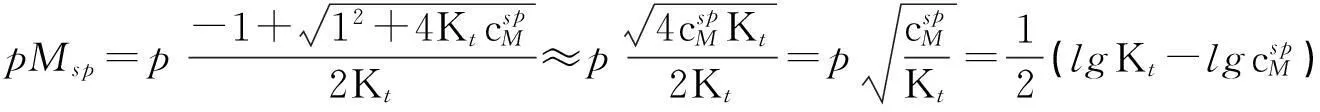
即化学计量点时的pMsp为：

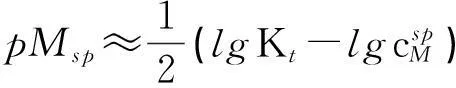
(2)

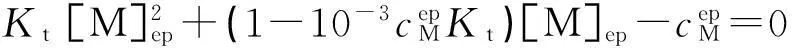
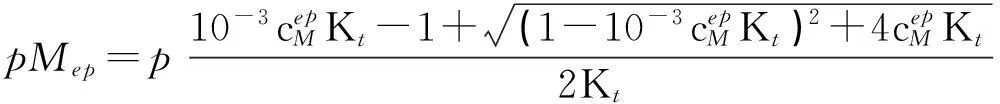
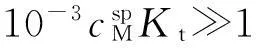
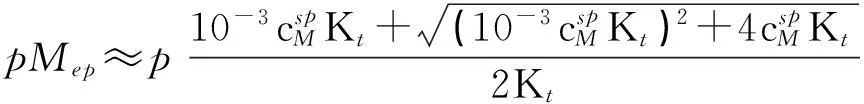
(3)

将式(2)和式(3)代入式(1)，整理得配位滴定突跃绝对值为：

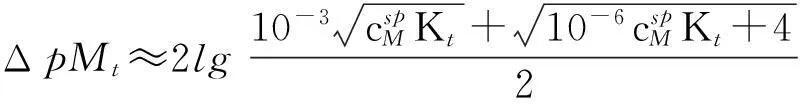
(4)

1.2　直接准确滴定条件

配位滴定的终点误差是指滴定终点与化学计量点不一致产生的误差，属于系统误差；滴定终点的不确定性是视觉误差，属于偶然误差。准确滴定是针对视觉误差而言的。假设指示剂的理论变色点和化学计量点完全一致，则视觉误差仍然会导致有ΔpM=±0.2～±0.5[1-3]的不确定性，文献[1-3]取视觉误差的最小值ΔpM=±0.2，由于配位滴定突跃的绝对值是在准确度不超过0.1%的条件下推导出来的，所以要实现准确滴定，就要保证滴定突跃绝对值ΔpMt≥0.4。根据式(4)，应有：

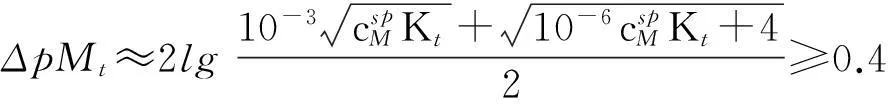
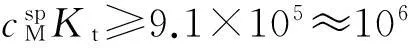
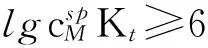
(5)

2一元强碱滴定一元强酸溶液

2.1　一元强碱滴定一元强酸滴定突跃绝对值的建立

由于一元强碱滴定一元强酸溶液要求滴定的准确度不超过0.1%[1-3]，所以滴定突跃绝对值定义为a=1与a=0.999时的pM之差的2倍，即ΔpHt=2(pHsp-pHep)。由文献[1]可知，强碱滴定一元强酸的林邦滴定曲线方程为Kt[H+]2+cHXKt(a-1)[H+]-1=0。按照与1.1节相似的方法，可得一元强碱滴定一元强酸溶液的滴定突跃绝对值为：

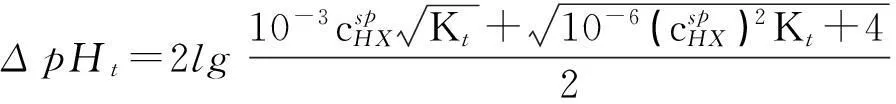
(6)

2.2　一元强碱滴定一元强酸的直接准确滴定条件

在酸碱滴定中，一般取ΔpH=±0.3[1-3]，由于滴定突跃绝对值是在准确度不超过0.1%的条件下推导出来的，所以要想实现准确滴定，就要求滴定突跃绝对值ΔpHt≥0.6。即：

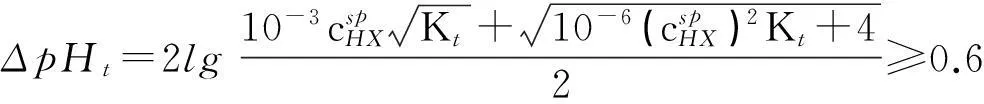
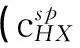
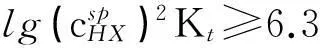
(7)

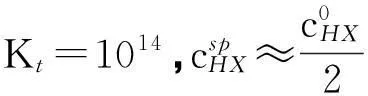
(8)

3沉淀滴定

3.1　沉淀滴定突跃绝对值的建立

由于沉淀滴定分析要求滴定的准确度不超过0.1%[1-3]，所以滴定突跃绝对值定义为a=1与a=0.999时pM之差的2倍，即ΔpMt=2(pMsp-pMep)。由文献[1]可知，沉淀滴定的林邦滴定曲线方程为Kt[M]2+cMKt(a-1)[M]-1=0。按照与1.1节相似的方法，可得沉淀滴定的滴定突跃绝对值为：

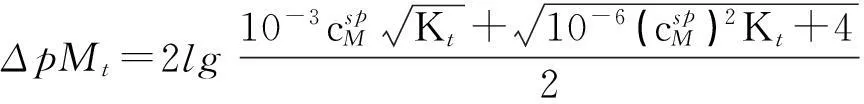
(9)

3.2　沉淀滴定的直接准确滴定条件

在沉淀滴定中，一般取ΔpM=±0.2[1-3]，由于滴定突跃绝对值是在准确度不超过0.1%的条件下推导出来的，所以要想实现准确滴定，就要求滴定突跃的绝对值ΔpMt≥0.4。即:

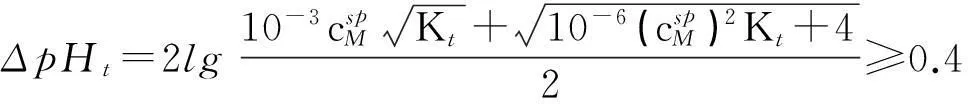
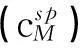
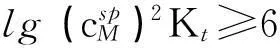
(10)

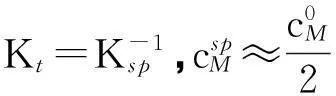
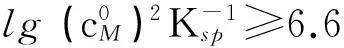
(11)

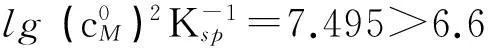
4简单氧化还原滴定

4.1　简单氧化还原滴定突跃绝对值的建立

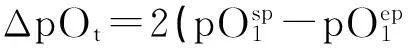
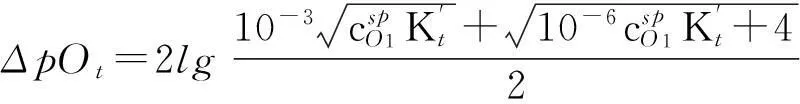
(12)

4.2　简单氧化还原滴定的直接准确滴定条件

对于简单氧化还原滴定，一般取ΔpO1=±0.2[4-5]，由于滴定突跃绝对值是在准确度不超过0.1%条件下推导出来的，所以要想实现准确滴定，就要使滴定突跃绝对值ΔpOt≥0.4。即:

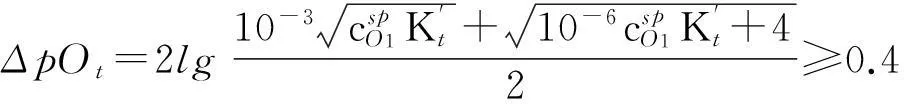
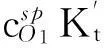
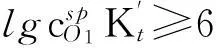
(13)

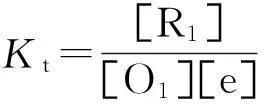
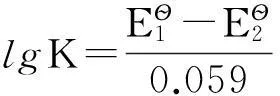
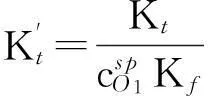
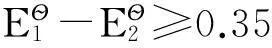
(14)

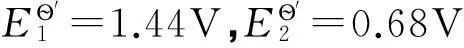
5结果与讨论

本文用林邦滴定曲线方程推导出几乎同一个数学模式的四大滴定分析的滴定突跃绝对值，并用其推导四大滴定分析的直接准确滴定条件。

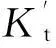
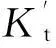
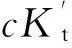
参考文献

[1]武汉大学.分析化学.第5版.北京:高等教育出版社,2006

[2]华中师范大学,东北师范大学,陕西师范大学,等.分析化学.第3版.北京:高等教育出版社,2002

[3]彭崇慧,冯建章,张锡瑜,等.分析化学.第3版.北京:北京大学出版社,1997

[4]孟凡昌,蒋勉.分析化学中的离子平衡.北京:科学出版社,1997

[5]孟凡昌,杨代菱.大学化学,2001,16(2):30

[6]雷良萍,龙文清.大学化学,2006,21(1):55

中图分类号O6；G64

doi:10.3866/pku.DXHX20150371