基于电子地图的非对称矩阵车辆路径问题研究
伊俊敏,苏志雄
(厦门理工学院管理学院,福建 厦门 361024)
基于电子地图的非对称矩阵车辆路径问题研究
伊俊敏,苏志雄
(厦门理工学院管理学院,福建 厦门 361024)
在建立路径问题二指数流量模型的基础之上,结合非对称性矩阵的变化进行灵敏度分析,并运用两种算法得到求解结果。多个实例的比较分析表明,非对称性问题与对称性问题是两个不同的问题,系数矩阵的差异最终带来目标函数值和基解的差异。城市物流配送实际案例检验表明,运用电子地图路线所得的非对称性距离矩阵,能有效缩短车辆路径总里程;相对于对称性矩阵车辆路径,非对称性距离矩阵车辆路径更符合当前物流的需求和实际情况,更具合理性。因此,城市物流配送应综合考虑各节点需求量和车辆选型,以平衡物流成本与服务要求。
城市物流配送;车辆路径;非对称矩阵;电子地图
城市物流配送伴随着城市生产、生活的发展而越来越普遍,它服务于城市及相近区域的货物取送需求,利用城市发达的道路交通网络,在经济合理区域内,按要求完成物流取送作业。在城市物流配送活动中,面对多客户需求,优化路线,降低成本就离不开车辆路径问题。自从Dantzig和Ramser于1959年从运输实践中提出车辆路径问题[1]以来,它一直是学术界和产业界十分关注的热点和难点问题。车辆路径问题(Vehicle Routing Problem,VRP)一般定义为:对一系列发货点和/或收货点,组织适当的行车路线,使车辆有序地通过它们,在满足一定的约束条件(如货物需求量、发送量、交发货时间、车辆容量限制、行驶里程限制、时间限制等)下,达到一定的目标(如路程最短、费用最小、时间尽量少、使用车辆尽量少等)。[2]尽管学界对此进行了大量的理论研究和实验分析,包括计算机求解大规模问题等研究进展不断涌现,但其研究结果在物流配送系统中的应用还是比较有限的。主要原因在于物流配送过程中涉及到货物、车辆、路线、时间和任务等条件交织的复杂性和变化性。
依据对物流配送过程复杂性考虑的侧重不同,VRP有多种分类方式,但带容量约束的车辆路径问题(CVRP)是最常见的VRP问题之一,也是物流配送车辆线路优化的基础。在CVRP模型中,各需求点两两之间的距离矩阵必须是确定已知的。传统的算例都是以二维平面来定位各需求点位置,以两两之间的直线距离构成一个对称性矩阵;但这只是一种理想假设,实际物流配送中各点间的距离是由它们之间的交通路线所决定的。[3]随着城市交通的发展,立交桥、转盘、高架路、隧道的不断出现丰富了道路的选择;单行线、禁左转、调头控制等交通管理措施也影响车辆路线的最终确定;甚至需要根据实时交通信息来动态确定车辆路线[4]。面对城市物流配送复杂的交通情况,CVRP模型的实际应用就不得不考虑如何构建合理的距离矩阵。尽管在CVRP各种算例的求解上研究很多,但是目前国内还未见考虑非对称距离矩阵的CVRP问题研究,本文以实际案例的电子地图非对称矩阵数据来探讨CVRP问题在城市物流中的应用。
一、基于电子地图的非对称距离矩阵的提出
近年来地理信息系统、遥感、测绘、计算机等技术的蓬勃发展为传统地图注入了新的活力,电子地图应运而生并发展迅猛,它的信息丰富,查阅显示方便,已经构成了一个庞大的地理信息系统。[5]成熟的商业地图在线软件功能强大,如谷歌地图和国内的百度、高德等地图等已经可以为交通出行、物流运输提供实时的信息和有价值的路线参考[6]。
在电子地图上,城市内各需求节点可以精确定位到所在街道门牌号上,两个节点间的驾车路线可由地图数据库按一定规则来确定,路线规则通常有多个选项供用户选择。例如百度地图给出“推荐路线” “最短路程”和“不走高速”3种选项,每种选项均给出路程和驾车时间,可用于实时导航。图1分别是两个节点间去程和回程的百度地图截图,可以看到,不仅距离有差别,更重要的路线有差别,去程先右转绕了一个大弯,还在立交桥下绕了一个小圈;而回程则简短直接得多,两个小右转后沿着一条马路直线走。在城市物流配送中,这种距离的差别特别明显,而在长途运输及物流中,这种短程的双向差别相对长距离就几乎可以忽略。

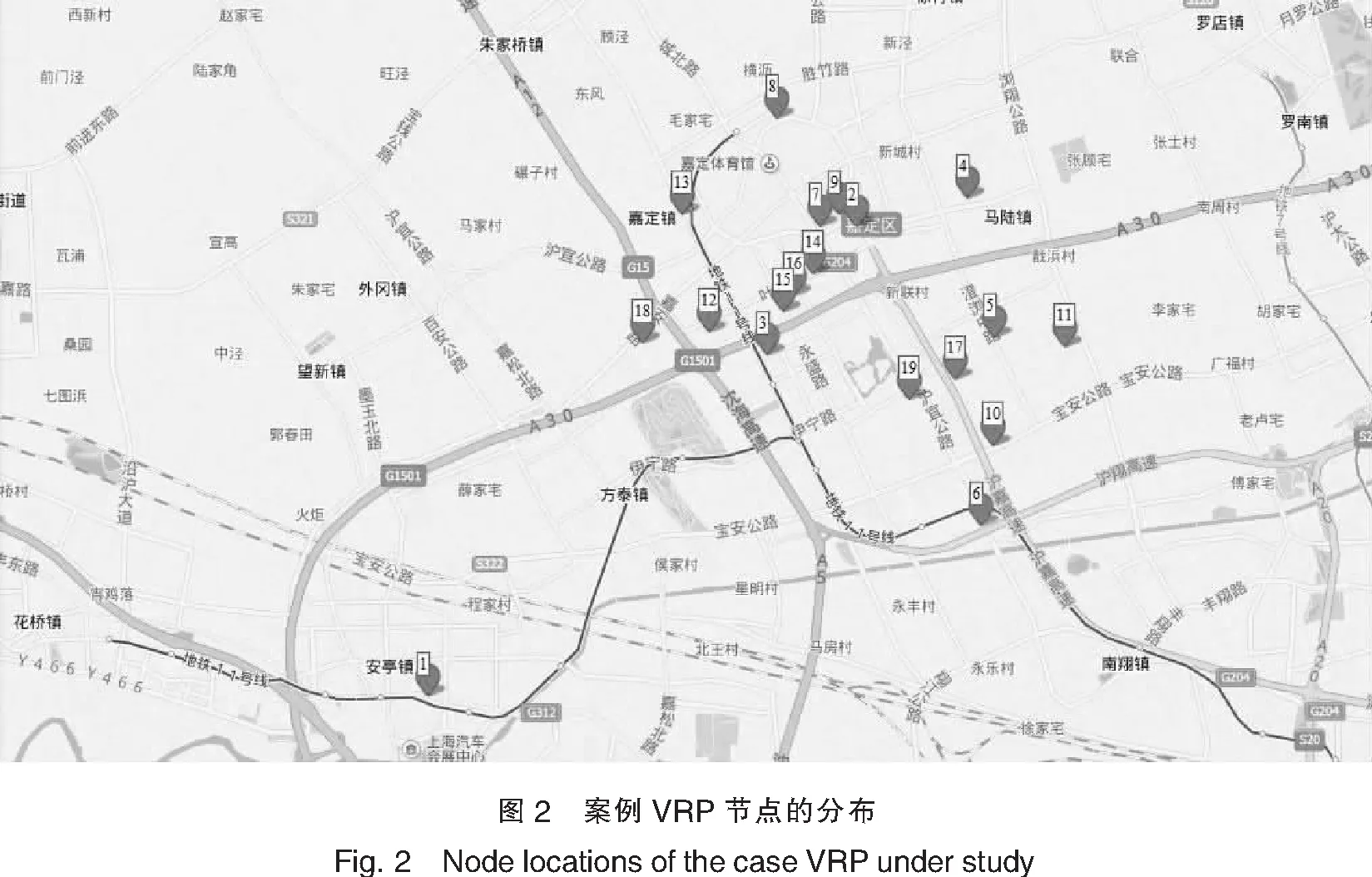
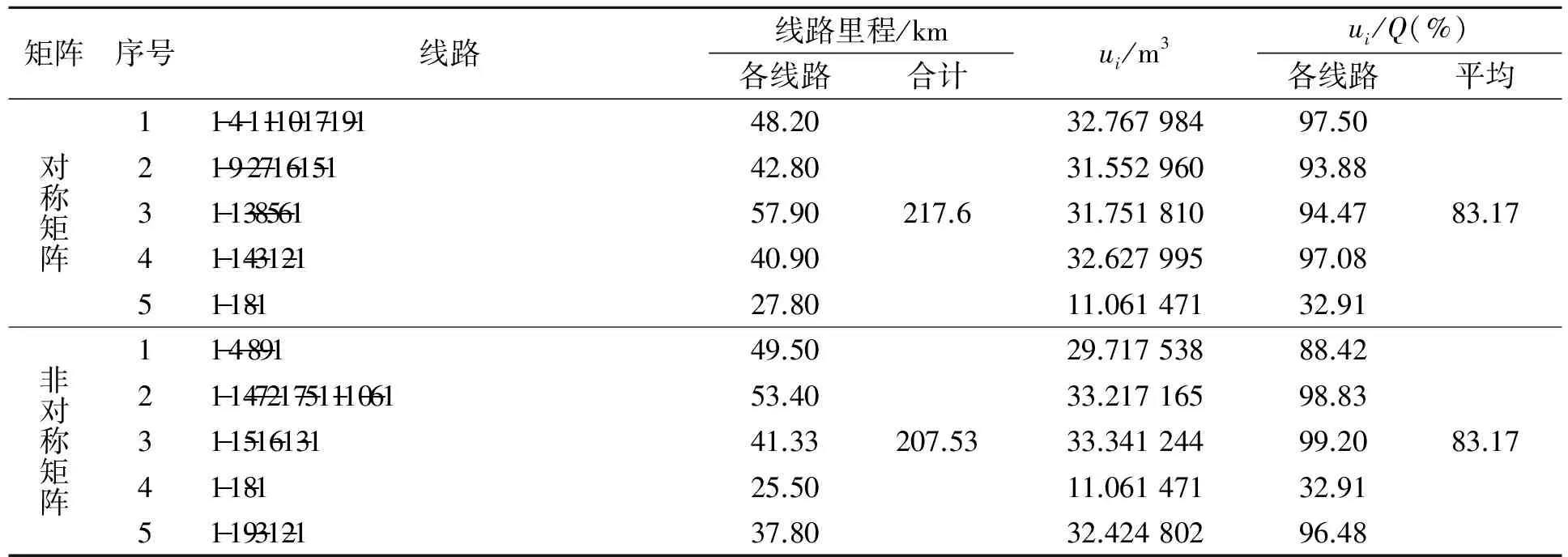
因此在实际问题中要考虑路线的差距给两两节点距离带来的差异,距离矩阵就应当是非对称的。为便于计算比较,我们不但给出非对称矩阵,还给出对称矩阵。不管是对称的,还是非对称的距离矩阵,它们的上半矩阵各元素均为{cij,i (1) (2) 考虑上述实际情况下的CVRP问题就是非对称矩阵的车辆路径问题AVRP,在单仓库、全同车型、每节点进出一次的基本假设不变的情况下,路径问题的目标函数总是minZ=CX。按照式(2)中对称矩阵和非对称矩阵情况的不同,CVRP和AVRP的目标函数可分别为minZ=SX和minZ=AX。AVRP问题模型采用二指数车辆流模型[7],目标函数写成求和形式如式(3)所示,其中xij为0~1变量,i,j= 2,…,n且i,j=1表示仓库。为此,模型表述如下: (3) (4) (5) (6) (7) ui-uj+Qxij≤Q-qj,qi+qj (8) qi≤ui≤Q, ∀i=2,…,n。 (9) 模型中,约束条件式(4)和式(5)是对各需求节点的访问约束,每节点只由一辆车来拜访,进出各一次;式(6)和式(7)为仓库节点约束,共m辆车从仓库出发并回到仓库;式(8)为子回路消除约束,式中Q为车辆容量,qj(j=2,…,n)为每节点需求量,ui(i=2,…,n)表示车辆访问节点i后的实际装车量,为连续变量。式(8)和式(9)这两个约束条件也共同形成车辆的容量约束。 从目标函数式(3)来看,从对称矩阵到非对称矩阵的不同体现在价值系数(两两距离)cij的变化,而针对价值系数的变化对问题最优解的影响可以采用灵敏度分析,这一分析主要考虑基变量和非基变量两种情况[8]。由于非对称矩阵涉及(n-1)2/2个价值系数的变化,相比对称矩阵时的最优解,非对称矩阵情况下,应当同时都有基变量和非基变量的价值系数变化,很容易超出基解不变条件下对价值系数变化所要求的范围,形成新的基解。即使基解不变,由于基解所对应价值系数的变化,最优解值也会发生变化。 本文案例是基于上海某物流公司的循环取货实例数据的VRP分析。案例中,仓库节点为该公司位于安亭的总库,在嘉定西部及城区范围内另有18个需求节点,19个节点在百度地图上的分布如图2所示。 以百度地图算出的两两推荐路线距离对称矩阵和非对称矩阵如图3所示。从图3可见,对称矩阵A是以右上角(即i 案例中车辆为载重8t的中型厢式货车,容积Q=33.609,各节点需求量为qj={11.901 92,31.141 474,15.713 732,2.257 92,1.005,0.794 88,13.854 51,0.1492 96,0.061 056,6.275 76,0.794 88,14.634 38,0.691 641,7.1035 96,11.603 268,10.228 988,11.061 471,0.488 448}。将两个不同的矩阵数据代入VRP模型中,采用LINGO精确算法和遗传算法得到的结果如表1所示。从表1可见,对称与非对称这两种情况除一条线路相同外,其他都不同;这条相同的路线1-18-1也因为矩阵元素不对称,而线路长度不一样。总的结果是5条路线中非对称矩阵时路径总里程更小。图4是非对称矩阵时电子地图上所反映的实际路线。 表1 对称矩阵与非对称矩阵的计算结果 我们对案例其他区域的节点问题也进行了计算,各区域的节点规模从6,9,11,13,16,17,19,28,32到47不等,它们的两两距离均按百度地图路线所得。其中有些区域分别考虑了选用不同车辆容积的两种情况,结果总结如表2所示。 表2 其他区域对称与非对称距离矩阵实例计算结果 *节点数超过20时,精确求解耗时过长,仅用遗传算法求解,不能保证一定是最优解。 可以看到,对称和非对称的最优解值均不相同,最优路线除个别路线相同外,一般均不同,也有对称与非对称的路线顺序刚好相反的,如2号的两个4)号路线和3号的对称2)和非对称1)路线。但是从0~1变量xij的值来看,不管是线路不同还是顺序不同,都是基变量的不同,也就是说矩阵的变化都引起了基的变化,最优解值当然更发生改变。例如,对表1中的例子,非对称矩阵S,Δcij最大值为-6.1,最小为0,Δcij的均值为-0.001 36,按百分比计最大为61.86%,平均差距为10.33%。非对称矩阵下目标函数值略小的原因不仅在于Δcij的均值小于0,还有基解的变化。 非对称矩阵VRP问题的最早并没有引起研究人员的重视,在经典直线距离对称矩阵算例的情况下,研究主要是追求各种算法的求解。最早考虑非对称矩阵的是采用精确算法的小规模问题[9],另外就是ADVRP(asymmetric distance-constrained vehicle routing problem)问题,但它同时对每辆车所走的总距离有一定限制[10-11],近年来,有研究开始考虑纯非对称矩阵情况的VRP问题AVRP,多算例证明非对称性问题和对称性问题是两个不同的问题[12]。由于非对称矩阵元素改变众多(共(n-1)2/2个),很难以对称的结果经过基变换得到非对称的结果,只能重新计算。因此结果可以是路线的不同,或者路线经过节点相同但顺序不同,但这都是反映基解的不同,目标函数值当然就更不一样。 另外,比较表2中相同结点的4与5,6和7的结果也表明,车辆容量也显著影响最终的路线结果,在城市配送小距离的范围内,车辆容量越小,需要的车辆数量就越多,同时所走的总距离也就越大。因为一些城市对配送货车的限制措施,物流配送需要综合考虑各节点需求量和车辆的选型,以平衡成本与服务要求。 城市物流配送因为受市内复杂的道路交通网络的影响,两两节点间的路线呈现不对称性,现代电子地图技术可以较好地描述展现这些线路的不对称性,从而为非对称性距离矩阵CVRP问题的求解带来了方便。本文以实际物流案例中的问题揭示了非对称矩阵车辆路径问题的建模、求解、灵敏度分析与实施的整个过程,为科学解决城市物流配送问题奠定了坚实的基础。若能进一步结合电子地图API编程与VRP模型求解,将为路径问题应用于物流实践提供实用化的可行方案。 [1]DANTIZIGGB,RAMSERJH.Thetruckdispatchingproblem[J].ManagementScience,1959,6(1):80-91. [2]刘云忠,宣慧玉.车辆路径问题的模型及算法研究综述[J].管理工程学报,2005,19(1):124-130. [3]李军,曹立明,王小平.基于GIS的物流配送路径计算[J].计算机应用与软件,2007,24(3):12-14. [4]李研锋,高自友,李军.基于实时交通信息的城市动态网络车辆路径优化问题[J].系统工程理论与实践,2013,33(7):1813~1819. [5]龙毅,温永宁,盛业华.电子地图学[M].北京:科学出版社,2006. [6]田智慧,苗全生,武舫.大区域物流配送中车辆路径选择的GIS研究[J].测绘科学,2008,33(5):155-157. [7]TOTHP.VIGOD.Models,relaxationsandexactapproachesforthecapacitatedvehicleroutingproblem[J].DiscreteAppliedMathematics,2002,123(1-3):487-512. [8]钱颂迪.运筹学[M].3版.北京:清华大学出版社,2003. [9]LAPORTEG,MERCUREH,NOBERTY.Anexactalgorithmfortheasymmetricalcapacitatedvehicleroutingproblem[J].Networks,1986,16,33-46. [10]LAPORTG,NOBERTY,TAILLEFERS.Abranchandboundalgorithmforthesymmetricaldistance-constraintedvehicleroutingproblem[J].MathematicalModelling,1987,9:857-868. [11]ALMOUSTAFAS,HANAFIS,MLADENOVIN.Newexactmethodforlargeasymmetricdistance-constrainedvehicleroutingproblem[J].EuropeanJournalofOperationalResearch,2013,226(3):386-394. [12]RODRIGUEZA,RUIZR.Astudyontheeffectoftheasymmetryonrealcapacitatedvehicleroutingproblems[J].ComputerandOperationsResearch,2012,39: 2142-2151. (责任编辑 马 诚) A Study of Vehicle Routes with Asymmetric Matrix based on E-map YI Jun-min,SU Zhi-xiong (School of Management,Xiamen University of Technology,Xiamen 361024,China) To deal with the asymmetric routes in unban delivery,a two-index vehicle flow model of CVRP was setup and solutions by two algorithms were conducted on many instances.Sensitivity analysis showed that the difference from asymmetric matrix leads to substantial change of objective value and optimal base,which implied that the asymmetric and symmetric problems are,indeed,two different problems.Using the asymmetric matrix from e-map service,the mileage of routes can be effectively shortened.The asymmetric matrix better meets the current logistics requirements and hence more practical and logical than the symmetric one.It is concluded that the node location,demand and routing should be synthesized for urban delivery to balance logistics cost and service. urban logistics and delivery;vehicle routing;asymmetric matrix;e-map 2015-04-13 2015-04-29 国家自然科学基金项目(71371162);福建省自然科学基金项目(2014J01271) 伊俊敏(1969-),男,教授,博士,研究方向为物流工程、集装箱运输管理。E-mail:yijunmin@xmut.edu.cn F252;O221;P289 A 1673-4432(2015)03-0032-07二、非对称矩阵CVRP问题及灵敏度分析
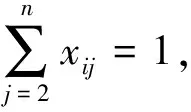
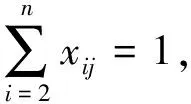
三、基于城市物流配送案例的AVRP算例


四、分析与讨论

五、结语

