红外光学材料折射率均匀性的测量不确定度评定

梁 菲，麦绿波，周桃庚，王 雷，沙定国

（1.北京理工大学 光电学院，精密光电测试仪器及技术北京市重点实验室，北京100081；2.中国兵器工业标准化研究所，北京，100089；3.西安应用光学研究所，西安，710065）

引言

与可见光光学材料一样，红外光学材料的折射率均匀性也是加工透射红外光学元件前必检的关键参数之一。文献报道，在可见光工作波段，其10－6量级的不均匀性，就将引起波长量级的波面变化［1］。可以推算到，红外光学材料各部分的折射率10－4～10－5量级的不一致，就将影响到红外光学元件加工中对透射波面误差的控制。目前，对可见光光学材料折射率均匀性的测量方法及其误差分析有不少的报道［2－5］，对红外材料折射率均匀性采用不贴置平板的多步红外干涉法，所用工作波长有1.53μm、3.39μm和10.6μm，但对其测量方法及其分析鲜见报道。本文基于制定红外光学材料折射率均匀性测量方法技术规范的需要，从测试原理出发，给出了一种相对合成标准测量不确定度的评定模型，依据实际测量的信息，在对影响测量结果的主要因素进行细致分析的基础上，找出其中的主要不确定度来源，得出四步干涉法测量红外光学材折射率均匀性的测量相对标准不确定度做到2×10－1～2×10－2，并进一步用MCM［6］（蒙特卡洛法）验证了 GUM 法［7］评定四步干涉法测量红外光学材折射率均匀性结果的有效性和合理性。同时，也验证了目前我国自行研制生产的红外硫系玻璃［8］样品的折射率均匀性达到或好于10－4量级，能满足高端红外仪器对红外光学材料折射率均匀性测量的要求。

1 四步干涉法及其测量特点

本测量问题系采用四步干涉法测量红外光学材料的折射率均匀性。其测量原理光路如图1所示，在指定的红外波长下，分别调试并测出图中所示4种测量光路的波前误差分布，进而计算得该平面工件样品的折射率均匀性偏差。

图1 四步干涉法测量原理Fig.1 Four-step interferometry measurement principle

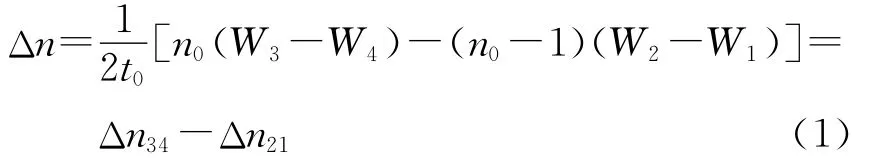
式中：W1为待检样品前表面Z1反射的波前误差，单位μm；W2为经待检样品透射后表面Z2反射回的波前误差，单位μm；W3为经待检样品透射，再经测试平面镜镜面Z3反射回的波前误差，单位μm；W4为移去待检样品后的干涉仪空腔波前误差，单位μm；n0为待检样品在该指定红外波长的折射率标称值；t0为待检样品的平均厚度，单位×10－3μm。

从测量原理公式可见，四步干涉法采用2张干涉图相减求得Δn21和Δn34后再相减的方式，消除了包括测试反射镜在内的干涉仪自身的恒定系统误差［9］，以及加工的样品2个面形光圈正负抵消部分误差的方式，有利于实现对样品折射率均匀性偏差的高准确度测量。与可见光干涉仪比较，红外干涉仪测试平面反射镜的面形光圈以及软件的算法误差都更易控制在可忽略的程度，剩下的影响因素主要来自红外探测器的噪声与红外光源准直系统剩余波差等的综合影响。仪器测量2次波前误差独立相减，使仪器测量Δn重复性增为原来的倍，而仪器剩余的系统波前误差却大致减为原来的10%。因此，四步干涉法测量2次波前误差相减后的主要误差影响项由原来的剩余系统偏差转为仪器随机测量噪声的重复性。例如，报道有35mm口径红外干涉仪的波前误差PV值的准确度λ／20～λ／50，进一步测量（W2－W1）、（W3－W4）PV值的准确度则还要好于λ／20～λ／50，因此四步干涉法较一步干涉法更有利于提高Δn的测量准确度。另外，需要指出，可见光可用貼置板法进行一步干涉测量的报道，但对于红外材料样品贴置用的匹配折射率高达2.5以上的液体很难寻觅，故至今也只见红外干涉仪仅采用四步干涉法的报道。

另外，估计其可测的范围。按一步干涉法测量折射率均匀性偏差的公式（2），该测量的PV值传递因子n0／2t0＝0.67×10－4／μm（n0＝2.7，t0＝20mm），按干涉图1／10至20个干涉条纹考虑，即Δn测量值可覆盖4.6×10－4～2.3×10－6（λ＝3.39μm）。鉴于四步干涉法采集4张干涉图的主要项W2和W3中叠加了样品的面形偏差，故有利于处理材料不均匀造成低至1／20条纹的干涉图。因此，四步干涉法测量红外折射率均匀性测量可覆盖4.6×10－4～1.1×10－6（λ＝3.39μm）。

2 测量不确定度的来源分析

2.1 测量原理方法的影响来源

基于上述原理，需适当控制好制备平行平面样品的楔角，一方面可免除因楔角过小使W1、W3干涉图中出现W2干涉图的条纹干扰，另一方面也可不计小楔角引起W1、W3干涉图像素错位而造成采样灰度误差的影响。另外，也不存在其他影响因素未计入而引起的Δn测量原理误差。

2.2 样品的影响来源

1）样品条纹气泡和杂质的影响

样品材料所含条纹气泡和杂质而产生的波前误差，原则上会对样品透射光路产生附加的波前误差。考虑到所测样品是事先经条纹气泡和杂质的检测合格后筛选出来的，条纹气泡和杂质所占材料面积的比例极小，对干涉图形不会产生明显干扰。因此，样品材料所含条纹气泡和杂质的影响大致在1×10－10，完全可忽略不计。

2）样品楔角的影响

有文献分析计算了该样品楔角引起测试光束偏折而造成干涉仪CCD采集图形像素错位的定量关系［2］，给出结论是，将样品楔角折合为干涉仪采样产生1个像素的位移会造成Δn测量原理的近似误差大致为4×10－7，作为控制样品楔角的上限。这里，结合红外材料样品的实际情况，假设样品厚度30mm，离开测试镜距离0.2m，以及一般干涉仪的像素分辨率0.413mm／pixel估计，该样品楔角控制在20′以内即可。因此，可以估计因该楔角造成Δn的原理测量标准误差不超出1×10－7，其影响也可忽略。

3）样品面形的影响

经对不同面形光圈样品的W2与W1、W3与W4计算机仿真计算Δn的结果分析，只要对3.39μm和10.6μm干涉仪分别控制样品面形加工光圈在1λ和2λ以内，由此引入测量Δn的影响低于2×10－8，可忽略不计。

4）样品平均厚度t0测不准的影响

样品平均厚度t0的测不准，会对测量W2和W3产生影响，进而对测量Δn12、Δn13乃至Δn产生影响。但考虑到用数显游标卡尺测量该样品t0的相对误差不超过0.67×10－3。按测厚均匀分布的假设，以及对样品测3次取平均，估计该游标卡尺

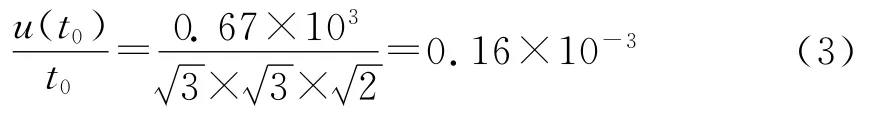
考虑 （1）式中测量 Δn12、Δn34与厚度t0的乘除关系，造成测量Δn12、Δn34的相对标准不确定度分量也为2×10－4。因此，样品厚度测不准的影响也可忽略不计。

5）样品折射率标称值n0测不准的影响

与可见光样品材料折射率测量方法相类似，红外样品材料折射率标称值n0也可用测量诸如直角对准照射封闭测角法、最小偏向角法、v棱镜折射法等精密测角的方法测得。不论哪种方法，其测量的相对标准偏差都容易控制在1×10－4以下。考虑（1）式中测量Δn12、Δn34的2项分量与折射率n0和（n0－1）的乘除关系，类同于样品厚度测不准的影响，都可忽略不计。

2.3 人机测量的影响来源

在本测量中，拟考虑的人机影响源包括红外干涉仪的测试平面反射镜、红外CCD采样分辨率，以及仪器测量中其他模块带入的系统效应，以及包括人工操作调整在内的仪器测量W1、W2、W3和W4中产生的综合随机效应的影响等4部分。

1）仪器中测试平面反射镜面形的影响

红外干涉仪器配备的测试平面反射镜的面形光圈，正常情况下应远好于样品的前后2个表面，按0.25λ（λ＝0.633μm），折合红外干涉仪工作波长为0.03λ（λ＝3.39μm），再折算为测量Δn的影响低于0.9×10－8，可忽略不计。

2）仪器中红外CCD采样分辨率的影响

参照可见光红外折射率均匀性测量的实验统计的报道［2］，CCD采样分辨率从606像素×606像素降低到101像素×101像素，其产生Δn的RMS值变化4×10－9，折算为Δn的PV值的变化不超过7×10－8。对于红外折射率均匀性干涉测量的情况，所用红外CCD等面阵传感器的采样分辨率对测量的影响也可参照此估计，其影响也可忽略不计。

3）仪器测量中其他模块带入的系统效应影响

红外干涉仪可选用的激光光源的工作波长有3.39μm、10.6μm等多种，其扩束与准直后的光束强度分布或多或少都存在偏离平面波的剩余波差，一般能控制在0.005λ以内。另外，干涉图采测量的相对标准不确定度分量为集与处理，包括插值和泽尼克多项式拟合等软件算法近似的影响，对波差测量的影响也能控制在0.005λ以内。最后，商品的红外干涉仪器校准证书能提供的仪器测量波差PV值能做到准确度λ／50，折算为Δn的PV值的变化不超过4×10－7。

4）仪器测量（包括人工操作调整在内）的W1、W2、W3和W4中随机效应的影响

对于红外干涉仪测量W1、W2、W3和W4中随机效应的影响，主要来自红外探测器等噪声，以及人工操作调整的影响。这部分影响的大小，一般可通过实验统计的数据来估计。对某型号红外干涉仪在短时间内相同测量条件下的空腔重复测量多批次的结果表明，其重复性（PV）0.005 7λ，未超出商品仪器公司提供的λ／100，折算为Δn的PV值的变化不超过2×10－7。

以上来自人机测量影响源大小的具体分析表明，特别当要求测量材料Δn至10－6量级时，尤其要注意控制好仪器测量（包括人工操作调整在内）的W1、W2、W3和W4中随机效应的影响，以及仪器测量中个别模块带入的系统效应的影响。后者需要商品的红外干涉仪器出示合格的校准证书，或者经多台仪器标准样品或比对样品的比对考核。

2.4 环境的影响来源

通过实验和分析，确定本测量的环境温度：检测室温度20±2℃，温度变化速度不大于1℃／h，样品在检测室内恒温12h以上；环境相对湿度：不大于70%或满足干涉仪正常工作湿度要求；环境振动：满足测量设备对环境的振动要求（隔振周期小于3Hz／s，振幅小于0.15mm）；环境气流：测量区域不允许存在明显扰动干涉条纹的气流（0.2mm／s）；环境洁净度：万级。当以上环境条件在正规的光学测量实验室中得到很好控制的情况下，可以不计对测量折射率均匀性的影响。即使有影响，实际上也部分体现在2.3所述的重复测量中所包含的随机效应的影响中。

综合以上环节中诸多影响要素的分析，干涉仪及其人员操作而造成测量波前误差W1、W2、W3和W4的影响，是最要注意控制好的关键因素。而样品折射率标称值n0定值，样品加工面形及其平均厚度测量，以及环境条件和测量原理方法的影响一般均可忽略不计。

3 测量不确定度的合成模型

由上述对各测量不确定度来源的细致分析中，影响Δn测量结果分散性主要来自（W1－W2）和（W3－W4）两部分的测量不确定度。基于此，建立如下便于评定的测量不确定度模型［10］。

由原理公式（1），样品折射率均匀性偏差的测量值Δn由Δn21、Δn34两项分量的代数和组成。而Δn21、Δn34分别与组合输入量（W3－W2）、输入量n0和t0，以及组合输入量（W3－W4）、输入量n0和t0之间均是乘除关系，即

故其相对测量标准不确定度为

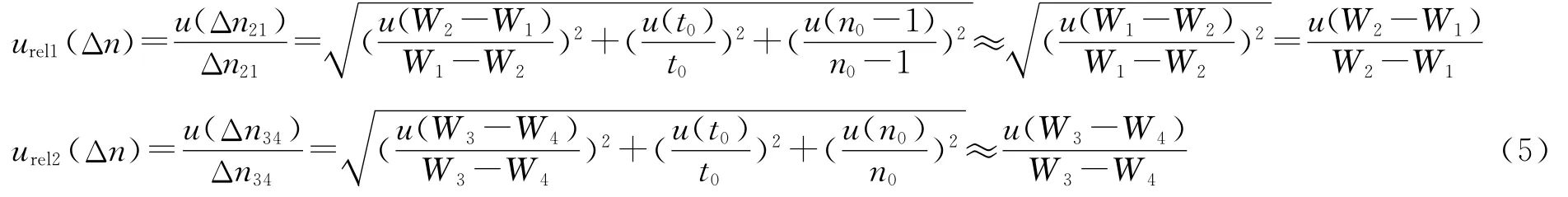
考虑到Δn21、Δn34之间完全非相关，Δn的相对测量标准不确定度为

4 测量不确定度分量的评定及其合成

根据（5）式和（4）式，只需评定2个主要的相对标准不确定度分量urel1（Δn）和urel2（Δn）。其中，u（W2－W1）和u（W3－W4）可按 W1、W2之间和W3、W4之间均完全正相关的情形考虑。调查红外干涉仪测量多个典型样品（折射率均匀性PV值覆盖 和3×10－6之间）的波差数据信息，再将仿真统计Δn21和Δn34后得到几种情形的（W2－W1）和（W3－W4）等数据，一并代入（4）式的结果见表1所示。

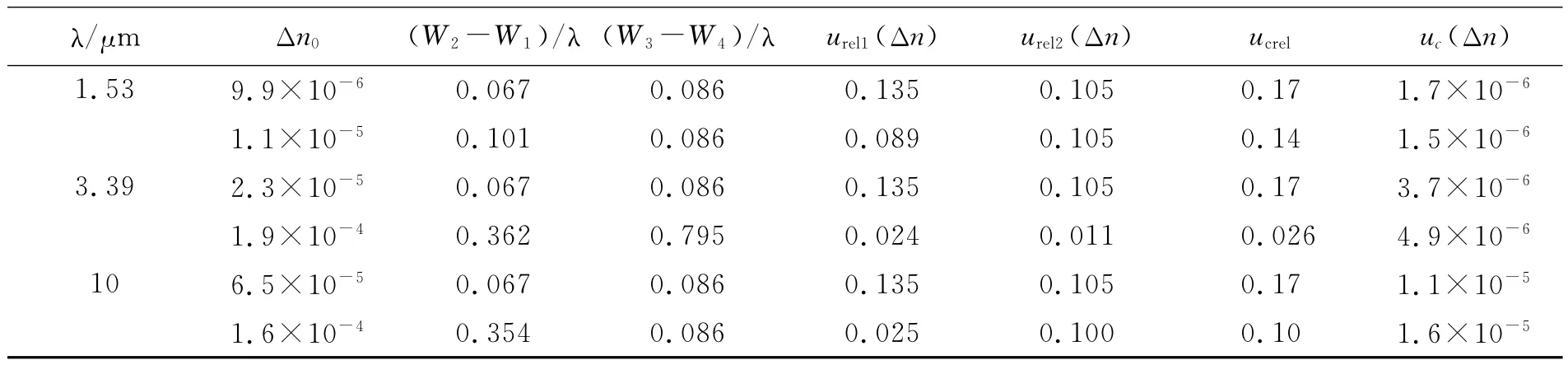
表1 不确定度分量及其合成评定数据（t0＝20mm，n0＝2.7）Table 1 Uncertainty components and synthetic assessment data（t0＝20mm，n0＝2.7）

5 讨论与总结

1）本文在细致分析和比较诸多不确定度源大小的基础上，突出了综合解决由四步干涉测量获得的经置换合并后的2个输入量（W2－W1）和（W3－W4）的相对标准不确定度分量大小的估计问题。如不确定度源信息汇总表2以及因果分析图2所示。不确定度信息源的占有充分与否，分析与处理是否可行与得当，是处理好测量不确定度评定问题的重要前提。

2）本文的测量虽属非完全乘幂形式的测量模型，但也采用了相对测量不确定度的处理方式，达到了极大的简化问题处理的目的。见诸多篇文献的报道，都因四步干涉法测量模型中，碰到难以确定诸多不确定源与其输出量之间的传递关系，进而无法准确合成得到最终的绝对测量不确定度的结果。本例表明，不仅限于乘幂形式的测量模型，在有些可能的情况下，采用相对标准不确定度的处理方式得到简化的合成评定模型，这也不失为一种可尝试的方式。

3）本文从实际出发，采用了GUM与MCM相结合的方式解决了对某些测量不确定度分量评定获取信息的困难，确保了主要不确定度分量评定的有效性。MCM基于概率分布传播的计算机仿真，已在微波功率、质量等输出量分布不对称的测量专业领域有了成功应用。本问题属光学测量专业领域，由于缺失（W2－W1）和（W3－W4）的数据信息，无法用GUM法去估计合成标准不确定度。这里，采用MCM仿真统计确定其数据信息，弥补了通常的GUM法仅依靠实验统计和非统计方法缺失数据信息的不足。需要指出的是，其实GUM法评定不确定度分量中的A类方法又可分为2种；即视实际情况，或选择基于实验统计的数据，或选择基于测量模型出发的MCM统计的数据。总之，即使所讨论的测量问题符合GUM适用的条件，也可以把GUM与MCM两者结合起来，来提高测量不确定度评定的有效性和合理性。

表2 不确定度源信息及其合成汇总Table 2 Information of uncertainty source and synthetic summary

图2 因果分析Fig.2 Causal analysis

本文撰写过程中得到中国兵器工业标准化研究所杨金侠研高工，西安应用光学研究所史继芳研究员，襄阳新华光学材料有限公司徐光以副总师、胡向平高工和唐雪琼高工，以及航天508所张继友高工等同志的大力支持和帮助，在此谨表谢意。

［1］ Guo Peiji，Yu Jingchi，Ding Zezhao，et al.High accuracy testing method of the homogeneity of optical glass［J］.Optical Techniquc，2001，27（6）：528-531.郭培基，余景池，丁泽钊，等.光学玻璃光学均匀性高精度测量技术［J］.光学技术，2001，27（6）：528-531.

［2］ Li Qiang，Liu Ang，Gao Bo，et al.Error analysis of absolute test method of inhomogeneity of optical materials［J］.Journal of Applied Optics，2008，29（1）：120-123.李强，刘昂，高波，等.光学材料光学不均匀性绝对测量误差分析［J］.应用光学，2013，34（3）：464-468.

［3］ Lin Juan.Interference absolute measurement for homogeneity of large-aperture optical glass［J］.Journal of Applied Optics，2008，29（1）：120-123.林娟.大口径光学玻璃光学均匀性干涉绝对测量方法［J］.应用光学，2008，29（1）：120-123.

［4］ Guo Peiji，Yu Jingchi，Ding Zezhao，et al.Absolute testing method of the homogeneity of optical glass［J］.Optical Technique，2003，24（3）：26-27.郭培基，余景池，丁泽钊，等.光学玻璃光学均匀性的绝对测量技术［J］.激光杂志，2003，24（3）：26-27.

［5］ Guo Peiji，Yu Jingchi，Ding Zezhao，et al.A high accuracy instrument of testing the homogeneity of optical glass［J］.Laser Journal，2004，25（3）：36-38.郭培基，余景池，丁泽钊，等.高精度光学玻璃光学均匀性测量仪研制［J］.激光杂志，2004，25（3）：36-38.

［6］ National Technical Committee of Legal Metrology Metering Management.JJF1059.2-2012.By monte carlo method for evaluation of uncertainty of measurement［S］.Beijing：China Standard Press，2012：6-14.全国法制计量管理计量技术委员会.JJF1059.2－2012.用蒙特卡洛法评定测量不确定度［S］.北京：中国质检出版社，2012：6-14.

［7］ ISO／IEC.Guide 98-3：2008Uncertainty of measurement-Part 3：Guide to the expression of uncertainty in measurement［S］.Swilzerland：ISO，1995.

［8］ Song Baoan，Wang Qiaofang，Zhang Yingzhao，et al.Optical inhomogeneity of IR se-based chalcogenide glasses and influencing factor analysis［J］.Infrared and Laser Engineering，2012，8（l）：1985-1988.宋宝安，王乔方，张莹昭，等.红外硒基硫系玻璃光学非均匀性及影响因素分析［J］.红外与激光工程，2012，8（l）：1985-1988.

［9］ Zhang Jianfeng，Cao Xuedong，Jing Hongwei，et al.Rotation method for system error calibration of interferometer［J］.Opto-Electronic Engineering，2011，38（12）：71-73.张建锋，曹学东，景洪伟，等.基于旋转法的干涉仪系统误差标定［J］.光电工程，2011，38（12）：71-73.

［10］Sha Dingguo，Wang Zhongyu，Wang Jinbo，et al.Error analysis and measurement uncertainty［M］.Beijing：China Metrology Publishing House，2003：124-148.沙定国，王中宇，王金波，等.误差分析与测量不确定度评定［M］.北京：中国计量出版社，2006：124-148.