补强片自动贴片系统高精度手眼标定方法
叶 溯,叶玉堂,刘娟秀,刘 霖,杜春雷
(1.电子科技大学 光电信息学院,四川 成都610000;2.中国科学院 光电技术研究所,四川 成都610200)
引言
柔性电路(flexible printed circuit,FPC)是以聚酯薄膜为基材制成的一种柔软可弯曲的印刷电路板。随着电子产品小型化和轻薄化的发展,使其得到了广泛的应用[1]。FPC材质柔软,需要在某些指定部位贴上补强片加强其硬度,而贴装误差在整个装联工艺中是造成产品缺陷的重要原因之一,故贴装性能好坏对生产过程的质量控制十分重要[2]。为了使补强片自动贴片系统(automatic stiffness bonder,ASB)完成高速下的高精度贴装,通常运用机器视觉辅助系统完成精确定位[3-4],同时需要对系统标定来消除误差。第一,对系统的几何误差进行测量和校正,提高运动机构的控制精度[5-6]。第二,进行手眼标定,消除系统中坐标系间相互转换计算的误差。解决eye-in-hand手眼标定问题等同于解方程AX=XB,需要机器人有足够的可控自由度,使其末端旋转轴能在二次运动中不平行[7]。当机器人末端只有一个旋转自由度时,为了得到方程的唯一解,需要对标定过程加入限制条件[8-10]。可以看出,不同设备的自由度不同,手眼标定中存在诸多的限制条件,无法使用统一的方法解决。
本文设计的ASB采用对称结构的直角坐标机械臂形式,提高了设备的刚性,减少了热变形的影响,但也导致了设备的可控自由度进一步减小,无法满足上文常规的手眼标定方法对设备自由度的要求。针对此类二维平面作业的情况,例如表面贴装设备、SCARA机器人等四自由度拾放机械臂[11],工业应用中将手眼标定简化为二维坐标平面的转换问题,由于齐次坐标转换矩阵没有完整的相机姿态信息,需要设置相机光轴垂直于工作平面[12-13]。此方法能够在设备自由度有限的情况下获取标定唯一解,但相机安装的垂直度偏差将会对标定结果引入误差,影响系统最终的拾放精度。为了消除相机安装的垂直度偏差带来的误差,本文提出了一种新的手眼标定方法,在能够得到手眼标定唯一解的同时,通过使用标定板得到相机的外参数,将外参数与二维手眼标定模型相结合,从而扩展为包括相机完整姿态信息的三维模型。其次,为了去除标定板高度带来的影响,使用厚度较小的菲林修正齐次坐标变换矩阵的Z方向分量。
1 手眼标定原理
本文设计ASB系统运动机构部分为直角坐标机械臂,如图1所示,夹具设为工具坐标系(tool frame),用于完成补强片的拾取和放置。吸附平台用于吸附固定FPC,作为机器人基坐标系X-Y工作平面。可移动的高分辨率相机对FPC上的贴合目标位置进行定位。为了精确定位需要对系统eye-in-hand手眼部分进行标定,将相机坐标系(camera frame)中的坐标Xcam统一转换为机器人基坐标系(base frame)坐标Xbase,用于计算系统的运动路径。

图1 ASB系统示意图Fig.1 Structure of ASB system
1.1 相机模型
描述相机成像的物理模型为小孔模型[14],如(1)式,内参数Min与外参数Mex通过标定得到,此时可以通过图像坐标计算出对应的空间坐标。其中cam为相机坐标系,obj为标定板坐标系。

1.2 Eye-in-hand手眼标定二维模型
Xcam与Xbase的转换关系,会随着夹具位置的改变而产生变化,如(2)式。而夹具与移动相机相对姿态不变,camHtool为固定值,可以通过手眼标定计算得到。其中Xtool通过Xbase平移变换得到,平移量可以从控制器中读取。

在手眼标定二维模型中,假设条件为相机光轴垂直于工作平面,故camHtool为二维齐次坐标变换矩阵:
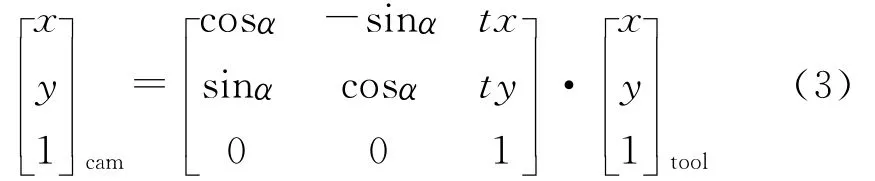
再将特定形状的图案设为基准标志点,通过拍照和测量等方法,获取标志点在cam和tool坐标系中的坐标值,再通过数值优化方法计算出2维手眼标定模型的camHtool。
1.3 Eye-in-hand手眼标定三维模型
由于ASB系统可控自由度有限,无法直接获得三维的camHtool,通过假设相机光轴垂直于工作平面,将三维camHtool简化为二维求解,但是这样也使得相机垂直度的安装偏差会对系统带来误差。
在手眼标定三维模型中,首先设置和拍摄不同旋转角度和倾斜角度的标定板,避免了系统可控自由度不足的影响,标定计算出相机外参数Mex,即cam坐标系与obj坐标系的相对位姿camHobj。其次放置obj标定板于base工作平面上,即obj坐标系与tool坐标系平行,如图2所示,计算出二维的齐次坐标转换矩阵objHtool,将包括相机完整三维姿态信息的camHobj与objHtool相乘,计算出三维camHtool,如(4)式:
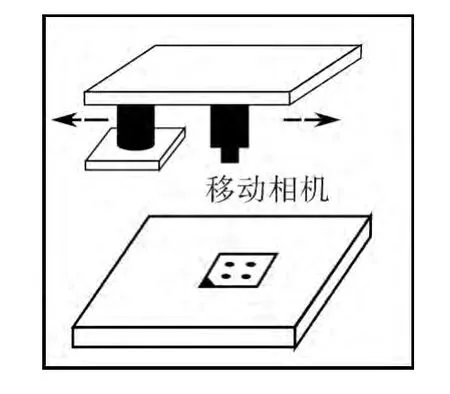
图2 Eye-in-hand手眼标定示意图Fig.2 Schematic of eye-in-hand calibration
将标定板的一个圆点中心作为标志点,控制移动相机在不同位置对标志点进行拍照,通过图像获取标志点在移动相机坐标系中的多组坐标值Xcom,其中标志点在obj坐标系X-Y 平面内,即zobj=0,因此 Mex中的旋转变换列向量[n,o,α],可以去除与zobj相关的α向量。
通过对大型船舶进出洋山港航行风险进行重点分析,结合现有的航道通航环境和交通流量特点,有针对性地建立相应的交通组织模式。该方案的实施还需引航站、海事局和港调等相关部门本着协同保障的原则,优化船舶进港顺序,最大化地缩短船舶等待时间,进而提高港口的运营效率。

将Xcam代入(5)式计算出Xobj,在拍摄同时,记录夹具当前位置并计算出Xtool。Xobj与Xtool间的齐次坐标变换矩阵如(6)式,通过数值优化方法可计算出objHtool。

得到了objHtool,同时根据外参数camHobj,就可计算出三维模型的camHtool。
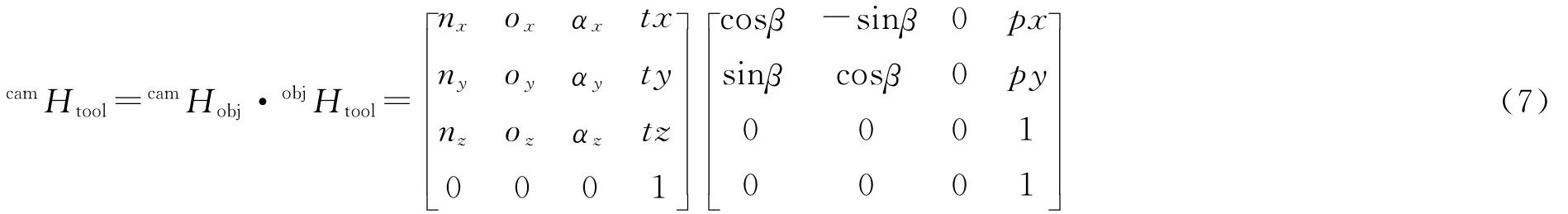
综上所述,通过手眼标定得到camHtool,代入(2)式可计算出目标图像坐标对应的Xbase,提供给运动控制器使用。
2 实验结果
将标定板放置于工作平面上,控制移动相机在不同位置对标定板进行拍照,计算出标定板中心圆标志点的坐标Xcam,同时记录拍照时夹具的位置,计算出当时的Xtool,得到10组手眼标定所需的数据,如图3所示。
利用标定数据,进行相机标定,得到内外参数。分别使用二维和三维手眼标定模型进行计算,如(3)式与(7)式,得到camHtool,同时将camHtool转换为姿态参数形式:


图3 不同位置的标定板图像Fig.3 Images of calibration boards at different positions
从表1可以明显看出,三维模型对比二维模型,还包括了相机在X轴与Y轴的旋转分量。

表1 对应的位姿参数Table 1 Pose parameters accorded with camHtool
为了对比二维和三维标定模型的计算精度,将2种模型计算出的camHtool代入(2)式与(4)式中,计算出对应X′tool,与标定用的原始数据Xtool相减,分别得到2种模型的计算误差,如图4。

图4 二维与三维模型的标定计算误差Fig.4 Calculation error of calibration with 2D model and 3D model
高精度的标定板一般使用玻璃和陶瓷作为基材,均具有一定的高度,需要考虑标定板高度带来的影响。为了消除标定板高度对成像物距造成的影响,使用厚度较小的菲林放置于工作平面,通过菲林上已知的图案标志,进一步修正物距,减小手眼标定的误差,如图5所示。

图5 实验系统图Fig.5 Experiment system
camHtool的Z方向分量TransZ作为移动相机成像的物距,记为tz。若按照已有的标定参数,tz=142.065mm,如表1所示。菲林上2个圆心的距离应为Δl′=9.0mm,如图6所示,但物距的改变会影响图像的放大率,通过菲林图像重新计算出的圆心距为Δl=8.948 7mm。按照(9)式,计算出修正后的物距tz′=142.88mm,消除标定板高度的影响,其中:
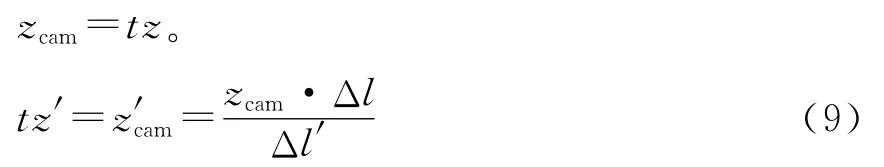
手眼标定误差是空间坐标在相机坐标系与机器人基础坐标系间的转换误差。为了说明tz修正前后对手眼标定误差的影响,利用菲林上同一圆心移动前后的图像,如图6所示,通过手眼标定结果camHtool,将cam坐标系中2次移动的圆心距离转换到base坐标系中,计算出的圆心移动距离与运动机构实际的移动距离相减就得到手眼标定误差。

图6 不同位置菲林的图像Fig.6 Images of films at different positions
控制移动相机在X与Y方向移动固定的距离,分别为18mm与13mm,共20次。结果显示,如图7所示,使用未修正的物距tz,有较大的误差均值,其绝对值在X与Y方向均超过了0.07mm,而使用修正后的物距tz′,能有效减小误差均值,消除了标定板高度对手眼标定造成的影响。
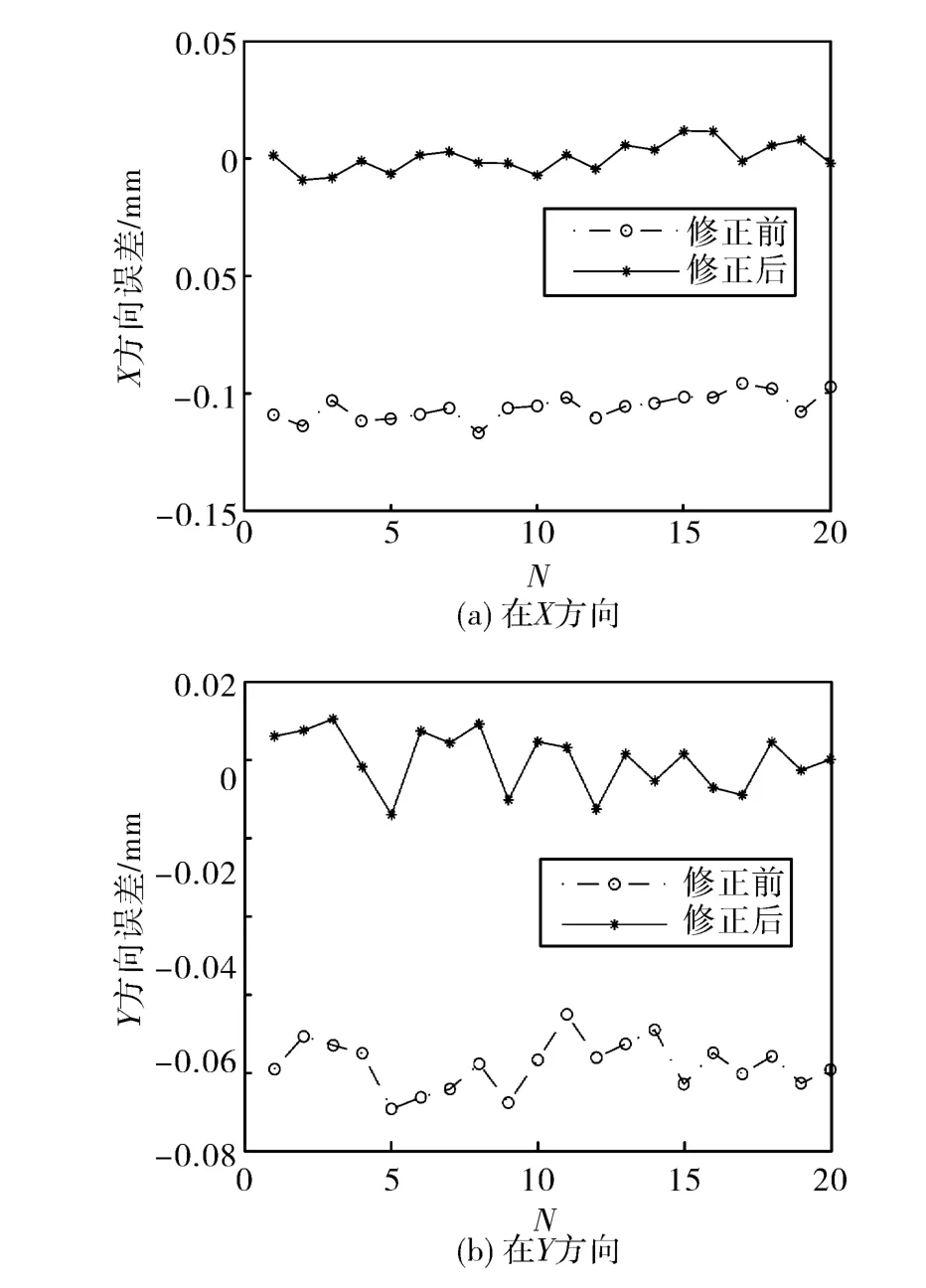
图7 tz修正前后,手眼标定误差Fig.7 Error of calibration before and after modification of tz
对齐次坐标变换矩阵Z方向分量tz修正后,系统手眼标定误差绝对值均未超过0.015mm,说明系统经过手眼标定后具有较高的控制精度。而描述设备的性能优劣一般使用制程能力指数(process capability index CPK)作为标准[15]。设定产品规格界限(specification limit)为0.12mm,计算X与Y方向对应的CPK值,并采用两者中最小的值作为当前设备的CPK。分别使用tz与tz′对应的2组误差数据计算,得到设备的CPK分别为0.837 5与5.388 5,可以看出tz修正后,误差均值绝对值减小,能够大幅提高设备的性能。
3 结论
第一,设置相机光轴垂直于工作平面,其X、Y轴的旋转角度分量均小于1°。使用二维模型标定仍具有较大的计算误差,最大的误差绝对值为5.278μm,使用我们提出的三维模型进行标定,其计算误差均小于0.1μm,相比二维模型误差降低了一个数量级,有效提高了标定计算精度。第二,通过厚度较小的菲林将标定的物距,即齐次坐标变换矩阵的Z方向分量进行修正,利用圆心移动前后的图像,计算出系统的手眼标定误差。结果显示,修正后手眼标定的误差绝对值小于0.015mm,具有较高的定位精度。同时以0.12mm作为SL,修正后设备的CPK从0.837 5提高到5.388 5,有效减小了标定误差均值,设备性能得到大幅提高。本文提出的手眼标定方法,在得到标定唯一解的同时,有效消除了相机安装的垂直度偏差带来的误差,去除了标定板高度带来的影响。同时此方法适用于高精度的工件拾放与贴装作业,对类似的视觉引导四自由度机械臂系统具有潜在的应用价值。
[1] Fjelstad J.Flexible circuit technology[M].Seaside,OR USA:Silicon Valley Publishers Group,1998:9-11.
[2] Hu Zhiyong.Trend in modern pick-and-place equipment[J].Equipment for Electronic Products Manufacturing,2002,31(2):69-72.胡志勇.贴装设备发展的新趋势[J].电子工业专用设备,2002,31(2):69-72
[3] Yu Zhanjiang,Wang Jingdong,Zhang Liuxin,et al.Detection method for tool setting gap of small lathe[J].Opto-Electronic Engineering,2012,39(10):122-127.于占江,王晶东,张留新,等.微小车床对刀间隙检测技术[J].光电工程,2012,39(10):122-127.
[4] Li Liangfu,Chen Weidong,Feng Zuren,et al.Vision calibration algorithm for object tracking and positioning[J].Journal of Applied Optics,2008,29(4):481-487.李良福,陈卫东,冯祖仁,等.目标跟踪与定位中的视觉标定算法研究[J].应用光学,2008,29(4):481-487.
[5] Castro H.A method for evaluating spindle rotation errors of machine tools using a laser interferometer[J].Measurement,2008,41(5):526-537.
[6] Schwenke H,Knapp W,Haitjema H,et al.Geo-metric error measurement and compensation of machines-an update[J].CIRP Annals-Manufacturing Technology,2008,57(2):660-675.
[7] Shiu Y C,Ahmad S.Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB[J].IEEE,1989,5(1):16-29.
[8] Everett L J,Burnett M S.Experimentally registering position sensors[J].IEEE,1996,1(1):641-646.
[9] De Ma S.A self-calibration technique for active vision systems[J].IEEE,1996,12(1):114-120.
[10]Zhuang H.Hand/eye calibration for electronic assembly robots[J].IEEE,1998,14(4):612-616.
[11]Shih C L,Ruo C W.Auto-calibration of an SMT machine by machine vision[J].The International Journal of Advanced Manufacturing Technology,2005,26(3):243-250.
[12]Seiko Epson Corporation.EPSON_vision_guide_60_manual[M].Japan:Epson Corporation,2012:237-255.
[13]Jiao Shengxi,Yue Xiaofeng,Wang Pingkai.Research of dynamic object positioning method of eye-in-hand vision[J].Optical Technique,2008,34(5):702-705.焦圣喜,岳晓峰,王平凯.手-眼视觉动态目标定位方法研究[J].光学技术,2008,34(5):702-705.
[14]Zhang Z.A flexible new technique for camera calibration[J].IEEE,2000,22(11):1330-1334.
[15]IPC-9850.Surface mount placement equipment characterization[M].USA:IPC,2002:13-15.

