铁路轨检车轴箱振动特性分析
肖 乾,方 骏,谭祖宾,袁其刚
(1 华东交通大学 现代轨道车辆研究所,江西南昌330013; 2 南车洛阳机车有限公司,河南洛阳471002)
铁路轨检车轴箱振动特性分析
肖 乾1,方 骏1,谭祖宾2,袁其刚2
(1 华东交通大学 现代轨道车辆研究所,江西南昌330013; 2 南车洛阳机车有限公司,河南洛阳471002)
轴箱是轮对与构架既相互连接又相互运动的关键部件,它起着承上启下的关键作用。铁路轨检车主要用于钢轨探伤,探伤设备的固定支架一般与轴箱相连,因此研究铁路轨检车轴箱振动特性对于提高探伤设备的使用寿命和探测精度具有重要意义。针对某型号轨检车建立整车车辆动力学模型,在此基础上建立了运动方程,得到车轮—轴箱系统频率响应输出;结合Hypermesh和Abaqus软件建立有限元模型并利用Block Lanczos算法进行了模态分析,得出轴箱前六阶的固有频率和主振型,得到第一阶模态固有频率为637.26 Hz;使用SIMPACK动力学软件建立轨检车动力学仿真模型,使轨检车在定义有激励的直线轨道上以70 km/h的速度行驶,计算出轨检车的车轮—轴箱系统垂向和横向频率响应输出并得出其共振频率,得到横向和垂向振动共振频率分别为20 Hz和63 Hz。可以发现第一阶模态固有频率远远大于其共振频率,因此轴箱的结构设计合理,在其工作速度范围内是安全的。
轨检车;轴箱;振动特性;模态分析
铁路轨检车主要用于钢轨探伤,探伤设备的固定支架一般与轴箱相连,因此,轴箱的振动特性将直接影响探测精度。另外,轴箱的振动特性对于列车悬挂装置选型及其自身结构优化也有非常重要的参考作用。轴箱振动特性研究一般通过动力学仿真或实际跟车检测两种方式进行,任尊松[1]等在车辆上布置加速度传感器[2]获得了武广客运专线高速动车组车辆轴箱、构架以及车体振动加速度曲线图,给出振动加速度功率谱密度计算方法。研究结果表明,与列车运行速度和车轮半径对应的轮轴转动频率在轮对、构架和车体振动中均有明显体现;列车运行速度越高系统振动加速度峰值越大,通过道岔时可激起车辆系统振动幅值更大的振动。刘楠[3]等利用有限元分析软件ANSYS对轴箱结构进行了静强度与模态分析,获得了轴箱结构的固有频率和振型,为了解结构的薄弱环节、动态性能评定及结构综合强度性能的评定提供依据。因此了解轴箱在特定激励的轨道上的振动特性和固有频率、主阵型,避免车轮—轴箱系统垂向和横向振动频率接近轴箱固有频率,对于保证探伤设备的探测精度具有重大意义。
1 轴箱动力学分析模型
强迫振动分析有两种不同的方法,时域分析法和频率分析法[4-5]。时域分析法所求的是系统的瞬态响应,需要用到数值积分,这种方法很容易处理系统的非线性特性。频域分析法所求的是系统对不同频率干扰的稳态响应,所得到的是系统的频率响应函数,优点是计算速度快,计算结果的分析也比时域法简单。根据轨检车的结构、装配特点建立动力学分析模型如图1所示,该模型由车体,转向架,车轮—轴箱系统,一系悬挂,二系悬挂组成。
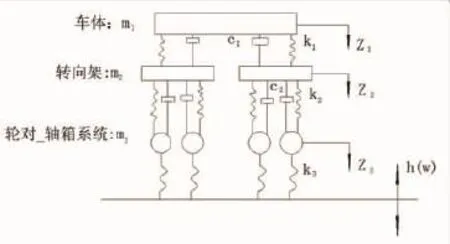
图1 完整的车辆动力学模型
图1中m1是车体质量;m2是转向架的质量;m3是车轮对—轴箱质量;K1,C1是二系悬挂的垂向刚度和阻尼; K2,C2是一系悬挂的垂向刚度和阻尼;K3是轮轨等效线性接触刚度[6]。轨检车的参数如表1和表2所示。

表1 轨检车质量参数
表2 轨检车悬挂参数
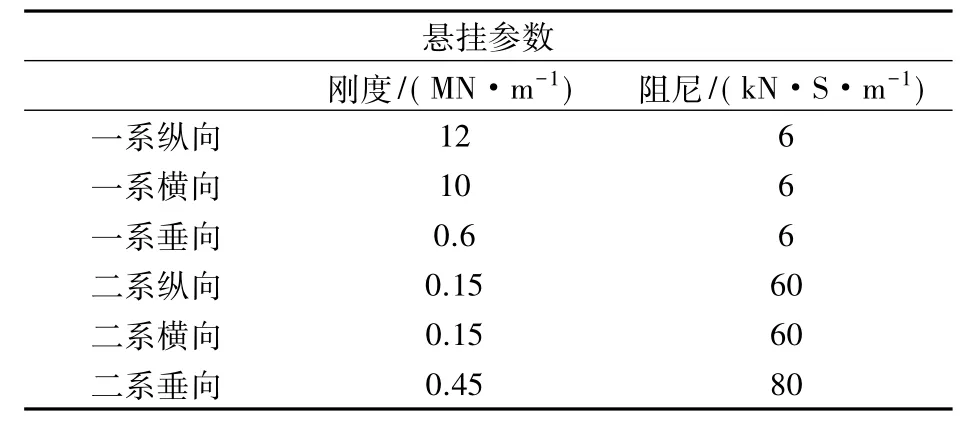
悬挂参数刚度/(MN·m-1) 阻尼/(kN·S·m-1)一系纵向 12 6一系横向 10 6一系垂向 0.6 6二系纵向 0.15 60二系横向 0.15 60二系垂向 0.45 80
建立车辆系统运动方程为:
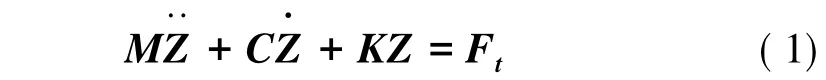
式中M为系统质量矩阵,C为系统阻尼矩阵;K为系统刚度矩阵;Z为位移矢量,Z=(Z1Z2Z3)T;Ft为来自于轨道的垂向干扰力矢量;Ft=F(w)=TTkKh(w),其中h(w),为线路干扰矢量;TTk为系统刚度关联矩阵的转置矩阵。
根据上面所述条件求解车辆系统运动方程(1)得到系统频率响应方程(2):
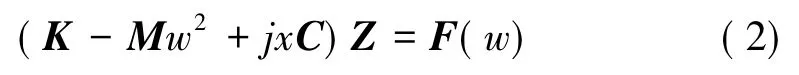
得到Z=(Z1Z2Z3)T,其中Z3为轮对—轴箱频率响应输出。
2 轴箱的振动特性求解
SIMPACK是机械系统动力学性能仿真分析软件,可以描述并预测复杂机械系统的运动学及动力学性能,可以分析其系统振动特性,受力状况以及零部件的运动位移、速度、加速度等[7]。利用动力学软件SIMPACK和动力学模型(如图1)建立轨检车整车动力学仿真模型如图2所示。轨检车模型参数如表1和表2所示,车轮名义滚动圆直径920 mm,车轮踏面为标准踏面S1002;轨距为1 435 mm。

图2 在SIMPACK中建立的车辆模型
建立车辆动力学模型时,为了更加真实模拟实际情况,研究轮轨之间的相互作用,特别是为了准确预测和分析车辆的动态响应,须要定义轨道激励[8-9],轨道随机激励是引起车辆系统产生各种动态响应的主要原因。SIMPACK软件主要提供两种轨道激励(Track Excitation and Rail Excitation),其中轨道不平顺是轨道激励之一,本次建模选择的是相对于轨道的类型,轨道不平顺选用的美国五级轨道谱,五级轨道谱密度函数表达式如式(3)所示[10]:

其中Sv(Ω)为谱密度,cm2·m/rad;Ω为空间波数,rad/m。
在SIMPACK前处理中,建立了车辆模型和定义了轨道激励,在车轮参考坐标系上定义传感器,使其在10 000 m直线轨道上以70 km/h行驶,可以计算出车轮—轴箱横向加速度和垂向加速度随时间的变化情况如图3和图4所示。
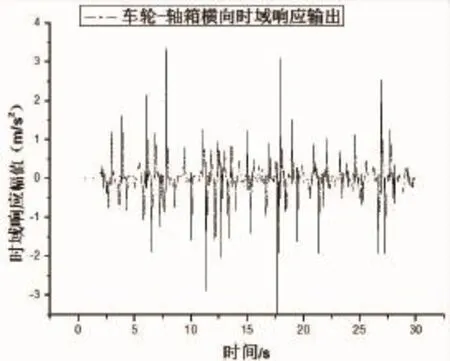
图3 车轮—轴箱横向加速度时域响应输出
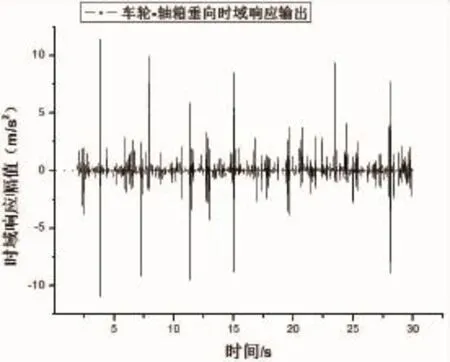
图4 车轮—轴箱垂向加速度时域响应输出
在上述两条曲线基础上可以得到车轮—轴箱系统横向和垂向频率响应输出,也能得到横向和垂向共振频率如图5和图6所示。
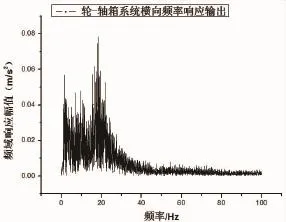
图5 车轮—轴箱横向频域响应输出
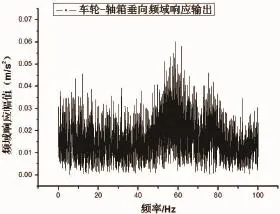
图6 车轮—轴箱垂向频域响应输出
将车轮与轴箱作为一整体对象,计算出如上图所示的车轮—轴箱时域响应输出和频率响应输出。从图3和图4可以知道横向和垂向时域响应输出在开始阶段波动比较剧烈,但是随后呈衰减趋势,直至列车运行平稳。图5和图6中表明车轮—轴箱系统横向振动共振频率约为20 Hz,垂向振动共振频率约为63 Hz。并且横向频率响应幅值在0~20 Hz比较大,垂向频率响应幅值在0~100 Hz范围内呈现极大值,这个极大值点就是共振频率。
3 轴箱模态分析
将轴箱模型导入网格划分软件Hypermesh[11]中划分网格。因为轴箱体形状比较复杂,所以在建立有限元模型时,对轴箱体采用四面体单元C3D4对结构进行离散,得到轴箱体有限元模型如图7所示。
建立有限元模型后,导入Abaqus中,利用Block Lanczos算法进行模态分析。网格划分的精度直接关系到有限元计算的准确性,网格划分力求几何形状与原结构一致,并采用疏密相结合的方式,轴箱装配体共离散成64 290个节点,261 635个单元。

图7 轴箱体有限元模型
模态分析的最终目标是识别出系统的模态参数,为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据[12]。通过Abaqus模态分析得到前6阶模态,得到相应固有频率和主阵型如图8和表3所示。
轴箱第1阶频率是637.26 Hz,轴箱体轴承孔绕X轴扭转变形,第2~6阶频率为1 090.5~1 778.7 Hz,轴箱体轴承孔和两只吊耳都发生变形,两只吊耳绕X轴扭转变形第1阶频率为1 485.9 Hz,轴箱底部也发生微小变形。
如果模态分析结果与车轮-轴箱系统横向和垂向频率响应输出的结果进行对比,可以发现,横向共振频率和垂向共振频率没有出现在轴箱模态中,并且第1阶模态远远大于上述两个频率。可以知道该轨检车轴箱结构设计较为合理,保证了测量仪器的精度,使轴箱的共振频率远远偏离第1阶固有频率。

图8 轨检车轴箱前6阶阵型

表3 轨检车轴箱模态
4 结论
(1)在Abaqus中给轨检车振动模态施加边界条件计算后,轴箱第1阶频率是637.26 Hz,轴箱体轴承孔绕X轴扭转变形,第2~6阶频率为1 090.5~1 778.7 Hz,轴箱体轴承孔和两只吊耳都发生变形,两只吊耳绕X轴扭转变形第一阶频率为1 485.9 Hz。
(2)在动力学软件SIMPACK中建立车辆模型,计算表明:车轮—轴箱系统横向振动共振频率约为20 Hz,垂向振动共振频率约为63 Hz。如果将该结果与轴箱振动模态的计算结果进行对比,可以发现上述2个频率没有出现在轴箱模态中,并且第1阶模态远远大于上述两个频率。
(3)通过上述分析知道该轨检车轴箱结构设计较为合理,保证了测量仪器的精度,轴箱的共振频率远远偏离第1阶固有频率,在第6阶模态时,轴箱两只吊耳绕X轴反向扭转变形,轴箱底部也发生微小变形。为增大轴箱底部刚度,可以在底部两只吊耳处分别增加两杆,连接吊耳底部和轴箱底部。
[1] 任尊松,刘志明.高速动车组振动传递及频率分布规律[J].机械工程学报,2013,49(16):1-7.
[2] 何声汉,林建辉,张兵.高速列车轴箱振动无线采集器[J].工程与实验,2010,50(1):54-57.
[3] 刘楠,傅茂海,金鑫,王平.机车车辆轴箱结构静强度与模态分析[J].机械制造,2013,43(3):17-23.
[4] 陆冠东.车辆系统动力学计算方法研究[M].北京:中国铁道出版社,2011.
[5] 倪振华.振动力学[M].西安:西安交通大学出版社,1988.
[6] 陈果,翟婉明,蔡成标,王其昌.传统车辆模型与车辆-轨道耦合模型的垂向随机振动响应分析及比较.[J].铁道学报,1999,21(5):70-73.
[7] 王晨,罗世辉,马卫华,刘韦,方翁武.直线电机悬挂结构的振动特性分析[J].铁道机车车辆,2013,33(4):66-70.
[8] 李增光,吴天行.浮置板轨道参数激励振动研究[J].振动与冲击,2010,29(2):17-21.
[9] 陈伯靖,钱小益,秦超红,李成辉.铁路钢轨受力分析模型比较研究[J].工程力学,2013,30(6):93-97.
[10] 翟宛明.车辆一轨道耦合动力学(第3版)[M].成都:科学出版社,2007.35-42.
[11] 周新建,王若飞,等.基于Hypermesh的立式加工中心立柱结构的拓扑优化[J].华东交通大学学报,2013,30(6):78-83.
[12] 鲁寨军,田红旗,周丹.270 km/h高速动车模态分析[J].中国铁道科学,2005,26(6):18-22.
Axle-box Vibration Characteristic Analysis for a Railway Track Inspection Vehicle
XIAO Qian1,FANG Jun1,TAN Zubin2,YUAN Qigang2
(1 Institute of Modern Railway Vehicles,East China Jiaotong University,Nanchang 330013 Jiangxi,China; 2 CSR Luoyang Locomotive Co.Ltd.,Luoyang 471002 Henan,China)
Axle-box is the key components of mutual connection and movement between wheel and frame.Railway track inspection vehicle is mainly used for rail flaw detection,and fixed bracket of inspection equipment are commonly connected to the axle-box,so vibration characteristic analysis is of great significance for improving the service life and detection precision of a flaw detection equipment.The dynamics model of the vehicle was established for one type of vehicle,and then the equation of motion was established and solved on this basis.The finite element model was set up by combination of Hypermesh and Abaqus,and Block Lanczos algorithm was used for the modal analysis.It obtained first six order natural frequency and main modes of the axle box.The first order modal natural frequency was 637.26 Hz.Vehicle dynamics simulation model was established by using SIMPACK.The inspection vehicle was driven at the speed of 70 km/h in linear orbit defining incentive.Vertical and horizontal frequency response output and its resonant frequency of wheel axle-box system were obtained respectively as 20 Hz and 63 Hz.It's found that the first order modal natural frequency is far greater than its resonant frequency,so the axle-box structural design is reasonable and safe within the scope of the work speed.
Inspection vehicle;Axle-boxes;vibration characteristics;modal analysis
U216.61
A
10.3969/j.issn.1008-7842.2015.02.03
1008-7842(2015)02-0010-04
)男,副教授(
2014-11-03)

