基于L1-L1范数的电学层析成像静态成像算法
王超,胡凤红,何晓蓉,秦伟刚,白瑞峰
天津大学 电气与自动化工程学院,天津 300072
基于L1-L1范数的电学层析成像静态成像算法
王超,胡凤红,何晓蓉,秦伟刚,白瑞峰
天津大学 电气与自动化工程学院,天津 300072
WANG Chao, HU Feng-hong, HE Xiao-rong, QIN Wei-gang, BAI Rui-feng
School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China
电学层析成像中静态成像算法的目标函数为电压测量值与电压计算值之间残差的范数与罚函数两项之和。目前,针对残差项的L1范数成像算法还较少,本文使用原始-对偶内点法,实现了目标函数中残差项和罚函数项均使用L1范数的重建算法,进行图像重建。研究表明使用基于L1-L1范数算法进行图像重建可获得较好的重建图像质量。
电学层析成像;静态成像算法;原始-对偶内点法;L1范数;L2范数
0 引言
1 基于L1-L1范数的静态成像算法
图像重建过程中目标函数的选取如式(1)所示。


对偶问题(D)用式(3)表示。

交换min和max,得到式(4)。

对(4)求偏导数,并令其为0,如式(5)。


原始对偶法不是解决原始的最小化问题和对偶的最大化问题,而是通过使原始对偶间隙为0,求解互补条件的最优解,原始对偶法如式(7)所示。

当且仅当满足条件(8)时,原始对偶间隙为0。

由于式(8)的两个条件不是处处可微分,原始对偶法可以转化为(9)。


由(10)~(12)得到变量更新的方程,式(13)。



对偶变量x、y是有范围限制的,每次更新值都要在设定范围之内,而不能确保是对偶问题的下降方向,因此传统的线性搜索不适用于求解迭代步长,本文采用步长法则更新 x、y[9],如式(16)所示。
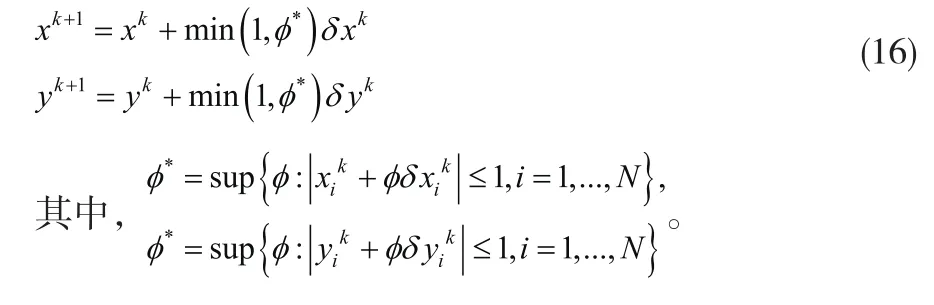
2 不同算法的对比研究
本文评价系统包括评价模型和评价参数,使用EIDORS和MATLAB实现。
2.1 算法的成像结果
为验证L1-L1算法的图像重建成像效果,共设置3个评价模型,包括单目标、双目标和三目标模型,其中目标物体的电导率是3 S/m,背景的电导率为1 S/m。同时与Newton-Raphson类经典算法中的TR、NOSER的成像效果进行对比研究,这两种算法的电压残差项和罚函数项均采用L2范数。不同算法的成像结果见图1。

图1 图像重建算法的成像结果
对于三种模型,TR、NOSER和L1-L1三种算法都可以分辨出目标的位置、大小。L1-L1算法重建目标的电导率大小接近真实分布,但是TR和NOSER算法重建目标的电导率和真实电导率分布相差较大。NOSER算法的成像结果中目标的形变较为严重,尤其是双目标模型最严重,已经无法估计出目标的形状。并且,TR和NOSER算法重建目标存在伪迹,L1-L1算法不存在伪迹。所有算法中,L1-L1算法重建目标的电导率和真实电导率分布相差最小的,成像目标的形变也是最小的,不存在伪迹,因此,L1-L1算法是表现最好的。
2.2 不同模型评价参数
本文选择图像误差[10]、算法的运行时间作为评价图像重建算法的评价指标,图像误差越接近0,图像质量越高,算运行时间越短,算法的实时性越好。定义评价指标如下所示。
2.2.1 图像误差

2.2.2 算法运行时间
算法的运行时间从逆问题计算开始,到计算出重建图像的电导率分布为止,不包括将重建图像显示出来的时间,单位为s。TR、NOSER和L1-L1三种算法的图像误差、运行时间分别如图2所示。

图2 不同算法的图像误差和运行时间
对于三种模型,三种算法的图像误差相差较大,从成像结果可以看出L1-L1算法成像效果最好,不存在伪迹,TR和NOSER算法存在伪迹,而且NOSER算法中双目标模型形变严重。评价参数中NOSER算法的图像误差最大,L1-L1算法的图像误差最小,与成像结果相吻合。从运行时间来看,NOSER算法运行时间最短,实时性好,L1-L1算法运行时间最长,实时性较差。
3 结论
对于三种模型,L1-L1算法成像结果基本上不存在伪迹,目标边界比较清晰,图像效果最好。TR和NOSER算法成像结果存在伪迹,目标边界比较模糊,但是NOSER算法运行时间较短,实时性好。因此,电压残差项和罚函数项均采用L1范数的算法成像不存在变形,目标边界清晰,要优于均采用L2范数的算法,但两项均采L2范数的算法实时性更好。
[1]肖理庆,王化祥,厉丹.改进Landweber预迭代ERT图像重建算法[J].中国电机工程学报,2013,33(23):118-125.
[2]肖理庆,王化祥,徐晓菊.改进牛顿-拉夫逊电阻层析成像图像重建算法[J].中国电机工程学报,2012,32(8):91-97.
[3]Vauhkonen M,Vadasz D,Karjalainen PA,et al.Tikhonov regularization and prior information in electrical impedance tomography[J].IEEE Trams Med Imaging,1998,17(2):285-293.
[4]Cheney M,Isaacson D,Newell JC,et al,NOSER:An algorithm for solving the inverse conductivity problem[J].Int J Imag Syst Tech, 2005,2(2):66-75.
[5]Yorkey TJ,Webster JG,Tompkins WJ.Comparing reconstruction algorithms for electrical impedance tomography[J].IEEE Trans Biomed Eng,1987,34(11):843-852.
[6]Rao LY,He RJ,Wang YH,et al.An efficient improvement of modified newton-raphson algorithm for electrical impedance tomography[J].IEEE Trans Magn,1999,35(3):1562-1565.
[7]Andersen KD,Christiansen E,Conn A,et al.An efficient primaldual interior-point method for minimizing a sum of Euclidean norms[J].SIAM J Sci Comput,2000,22(1):243-262.
[8]Borsic A,Adler A.A primal-dual interior-point framework for using the L1 or L2 norm on the data and regularization terms of inverse problems[J].Inverse Probl,2012,28(9):95011-95037.
[9]Murai T,Kagawa Y.Electrical impedance computed tomography based on a finite element model[J].IEEE Trans Biomed Eng,1985, 32(3):177-184.
[10]Yang WQ,Peng LH.Image reconstruction algorithms forelectrical capacitance tomography[J].Meas Sci Technol,2003,14(2):1-13.
Electrical Tomography Static Reconstruction Algorithms Based on L1-L1 Norm
The objective function of the static imaging algorithm in electrical tomography contains two terms, one is function of residual error between measurement boundary voltage and computational voltage, and the other is the penalty function.At present, the L1 norm imaging algorithm for the residual term is still less.The primal dual interior point method is used to reconstruct the image with both the residual term and penalty function using L1 norm.The research shows that the image reconstruction using the L1-L1 norm algorithm can obtain high-quality reconstructed images.
electrical tomography;static imaging algorithm;primal-dual interior point method;L1 norm;L2 norm
静态成像算法是当前电学层析成像(Electrical Tomography,ET)技术研究的热点[1-2]。其目标函数为电压测量值与电压计算值之间残差的范数和罚函数两项之和。Newton-Raphson类算法是静态成像中的经典算法,其目标函数的第一项为残差的L2范数,罚函数多数采用L2范数。如Tikhonov正则化算法(TR)、Levenberg-Marquart算法、牛顿一步迭代算法(Newton’s One Step Error Reconstructor,NOSER)和同伦Newton-Raphson算法电压残差项和罚函数均采用L2范数[3-6]。
L1范数应用较少的重要原因在于L1范数是不光滑的函数,不是处处可导,因此求解困难。Andersen等[7]证明原始-对偶内点法在求解L1范数方面比其他经典的方法具有独有的优势[8]。本文采用原始-对偶内点法,实现了残差项和罚函数项均采用L1范数的图像重建。
TM934.7
A
10.3969/j.issn.1674-1633.2015.07.005
1674-1633(2015)07-0016-03
2015-06-28
作者邮箱:wangchao@tju.edu.cn
——随钻钻孔电磁波层析成像超前探水设备及方法研究

