基于双前沿面数据包络分析的循环全局Malmquist指数
王应明,蓝以信
(福州大学决策科学研究所, 福建 福州 350116)
基于双前沿面数据包络分析的循环全局Malmquist指数
王应明,蓝以信
(福州大学决策科学研究所, 福建 福州 350116)
利用全部时期的技术构成的前沿面为参照,将双前沿面数据包络分析下的Malmquist指数拓展为双前沿面数据包络分析下的全局Malmquist指数。该全局Malmquist指数不仅较好地综合了乐观前沿面和悲观前沿面两部分信息,而且满足循环性检验;不仅可以避免由于前沿面选择的不同而导致的差异,还可以避免因时期选择的任意性而导致的差异。将其用于福建省工业行业2001-2008年的全要素生产率分析,研究结果较好地说明了该方法的有效性和实用性。
数据包络分析;Malmquist指数;双前沿面数据包络分析;全局Malmquist指数;循环性检验
1 引言
Malmquist指数最初是由瑞典经济学家Malmquist[1]在1953年提出的。Malmquist利用缩放因子之比来构造消费数量指数,此即为最初的Malmquist指数。由于该缩放因子与Shephard[2]在生产分析中提出的距离函数存在对应关系,受此启发,Caves等[3]将这种思想运用到生产分析中,通过距离函数之比构造生产率函数,并将此指数命名为Malmquist生产率指数 (以下简称为Malmquist指数),并且证明在一定条件下,该指数的几何平均形式与Tornqvist指数等价。但是,Caves等人没有给出距离函数的测度方法,因而该指数还只是一种理论指数。Färe等[4]结合Farrell[5]效率评估的观点以及Caves等[3]构造的Malmquist指数,通过数据包络分析(Data Envelopment Analysis,DEA)方法来求解距离函数,构造了基于DEA的Malmquist指数,使得该指数由理论指数转变为一种实证指数。并将该指数分解为两部分,即技术效率变化指数和技术进步指数。随后,Färe等[6]提出了DEA-Malmquist指数三部分的分解方法,即在两部分分解的基础上把效率变化更进一步分解为规模变化和纯技术效率变化。对此分解是否会导致内部的不一致性,学术界也存在着一些分歧。本文在此不详细讨论这些分歧,而仍沿用两部分分解方法。关于三部分分解及其存在的问题,有兴趣的读者请参阅Ray和Desli[7], Färe等[8], Lovell[9],Grosskopf[10]以及章祥荪和贵斌威[11]等研究。随着Mlamquist指数的广泛应用,学者们提出了一些新的DEA-Malmquist指数。主要有:Chung等[12]构建的Malmquist-Luenberger 生产率指数;Griefll-Tatjé 和 Lovell[13]提出的广义的Malmquist 指数;Chen Yao[14]提出了非径向的Malmquist指数;Pastor 和 Lovell[15]提出的全局Malmquist指数;Lo 和 Lu Wenmin[16]提出的基于SBM模型的Malmquist指数;Kao[17]提出的基于共同权重的全局Malmquist指数;Oh[18]提出的全局Malmquist-Luenberger指数;Pastor 等[19]提出的采用两个相邻时期的技术共同作为参考技术的Malmquist指数;Tohidi和 Razavyan[20]提出的利润型全局Malmquist指数以及Kao和Hwang[21]提出的含有多个时期的两阶段生产过程中的Malmquist指数测算方法。
应用方面,基于DEA的Malmquist指数被广泛用于生产率分析。例如:李小平和朱钟棣[22]利用其分析了1986-2002年间中国制造业各行业的全要素生产率,并且探讨了该生产率增长与经济增长之间的关系。李廉水和周勇[23]以全国35个工业行业为样本,运用DEA-Malmquist指数,将广义的技术进步分解为科技进步、纯技术效率和规模效率三部分,并结合计量经济中的方法估算了这三部分对能源效率的作用。陈勇和李小平[24]用其测算了我国工业行业1985-2003年间的技术进步以及其转型的特征。Odeck[25]将其用于分析1987-1997年间挪威东部农业部门的生产率变化情况。解百臣和杜纲[26]针对实际应用中存在的期望效用最大化的一类企业生产率分析提出了基于效用函数的Malmquist指数,并将其应用于火电类上市公司的实证分析。Gitto和Mancuso[27]将该指数与Bootsrap重抽样技术相结合分析了2000-2006年间意大利28个机场的生产率变化情况。Egilmez和McAvoy[28]将DEA-Malmqusit指数模型用于分析美国50个州2002-2008年间在减少公路交通方面重大事故的效率和生产率。
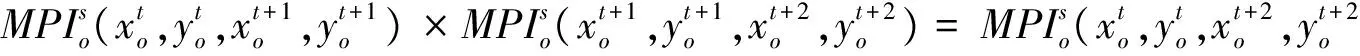
2 双前沿面DEA-Malmquist指数
2.1 基于乐观前沿面的DEA-Malmquist 指数
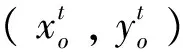
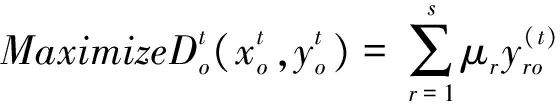
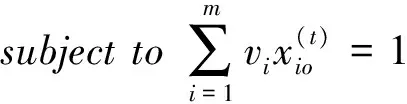
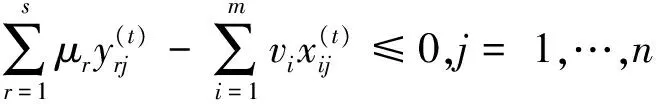
μr,vi≥0,r=1,…,s;i=1,…,m,
(1)
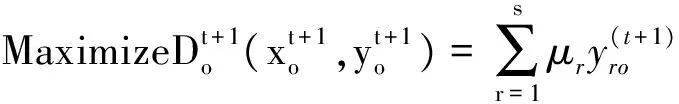

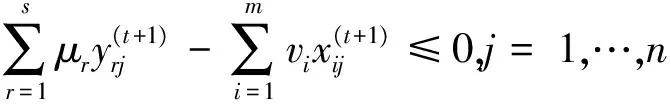
μr,vi≥0,r=1,…,s;i=1,…,m,
(2)
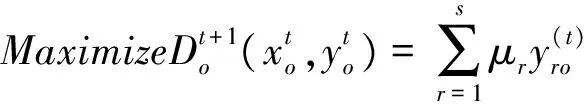
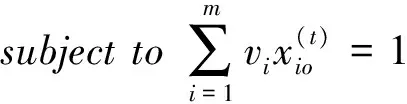
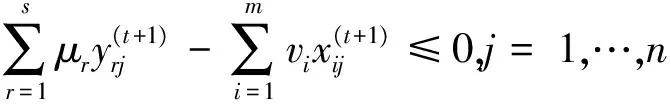
μr,vi≥0,r=1,…,s;i=1,…,m,
(3)

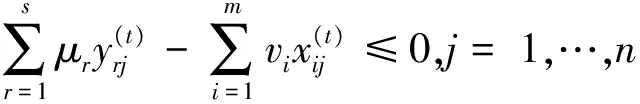
μr,vi≥0,r=1,…,s;i=1,…,m,
(4)
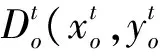
MPIo(optimistic)=
(5)
该指数度量的是DMUo从t到t+1时期生产率的变化情况。如果MPIo(optimistic)>1,则表示生产率增长;如果MPIo(optimistic)=1,则表示生产率不变;如果MPIo(optimistic)<1,则表示生产率降低。
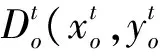
MPIo(optimistic)=
(6)
其中第一部分为OECo度量的是DMUo乐观前沿面下技术效率的变化情况,当OECo>1意味着效率提高,反之则意味着效率降低,如果OECo=1,则表明效率无变化;而第二部分度量的OTCo是基于乐观前沿面t到(t+1)时期的技术进步变化情况。
2.2 基于悲观前沿面的DEA-Malmquist 指数
传统的效率一般都是建立在效率为1的决策单元构成的“好”或者是“乐观”的前沿面上。Wang Yingming等[29]将评价值限定在大于等于1的水平下,这样测得的所有评价值为1的决策单元将构成一个“最差”或者是“悲观”的前沿面。为了叙述简洁,有关悲观效率的模型参见Wang Yingming等[29-30]。悲观前沿面下的Malmquist指数可以通过求解如下四个模型来获取需要的四个距离:
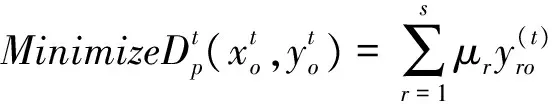
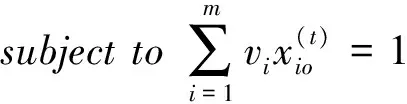
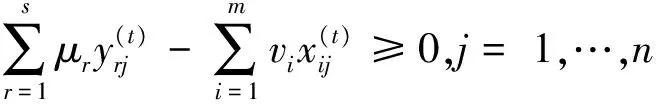
μr,vi≥0,r=1,…,s;i=1,…,m,
(7)
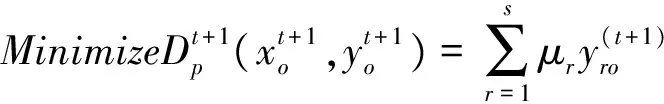
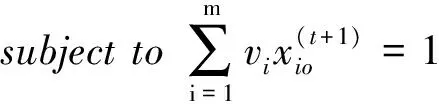
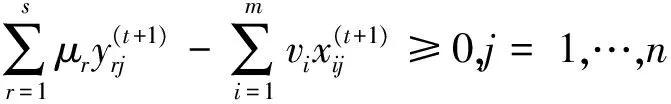
μr,vi≥0,r=1,…,s;i=1,…,m,
(8)
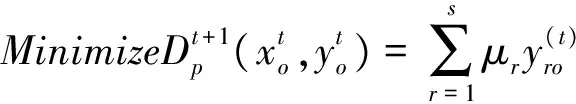
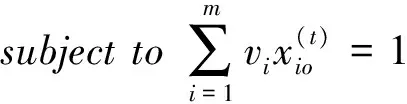
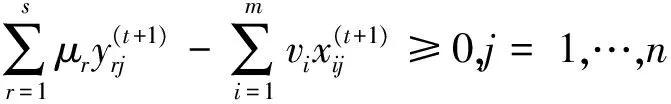
μr,vi≥0,r=1,…,s;i=1,…,m,
(9)
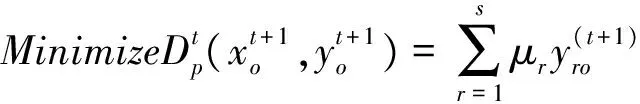

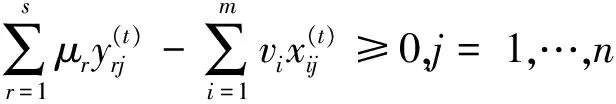
μr,vi≥0,r=1,…,s;i=1,…,m,
(10)
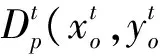
MPIo(pessimistic)=
(11)
如果MPIo(pessimistic)>1,则表示在悲观前沿面下生产率的增长;如果MPIo(pessimistic)=1,则表示在悲观前沿面下生产率不变;如果MPIo(pessimistic)<1,则表示在悲观前沿面下生产率的降低。
与乐观前沿面下的指数相似,(11)中的生产率指数也可以分解为两部分:
MPIo(pessimistic)=
(12)
其中第一部分PECo度量的是DMUo悲观效率的变化情况,PECo>1意味着效率提高,反之则意味着效率降低,如果PECo=1,则表明效率无变化;而第二部分PTCo度量的是悲观前沿面下从t到(t+1)时期的技术变化情况。
2.3 双前沿面下的DEA-Malmquist 指数
基于乐观前沿面的DEA-Malmquist指数和基于悲观前沿面的DEA-Malmquist指数是建立在不同的参考面上的,反映的是不同前沿面下的生产率指数变化的情况。为了避免前沿面选择的不同导致的差异,文献[31]将两指数用几何平均的方式进行了综合,得到如下的双前沿面下的DEA-Malmquist指数:
MPIo(DFDEA)= [MPIo(optimistic)·MPIo(pessimistic)]1/2=ECo·TCo
(13)
其中ECo=[OECo·PECo]1/2和TCo=[OTCo·PTCo]1/2分别度量的是从t到 (t+1) 时期DMUo的平均技术效率的变化和平均技术进步的变化。
3 双前沿面下的全局DEA-Malmquist指数
上述双前沿面下的Malmquist指数一般情况下不满足指数检验中的循环性检验。在度量技术变化时,Pastor等[15]将效率前沿设定为全体时期,从而计算所得的t时期和 (t+1)时期的技术变化均参照全体时期的生产技术。因而测得的技术效率变化与技术进步变化具有可比性,并且满足循环性检验。然而,Pastor等[15]所得的结果仅为乐观前沿面下的全局DEA-Malmquist指数,忽略了悲观前沿面的影响。有鉴于此,本文将全局的思想引入双前沿面下的DEA-Malmquist指数的计算中,将双前沿面下的DEA-Malmquist指数拓广为双前沿面下的全局DEA-Malmquist指数。拓广后的指数能够满足循环性检验。
3.1 基于乐观前沿面下的全局DEA-Malmquist指数
乐观前沿面下的全局DEA-Malmquist指数需要测算t时期和 (t+1) 时期相对全体时期的效率变化值,即求解如下两个模型:
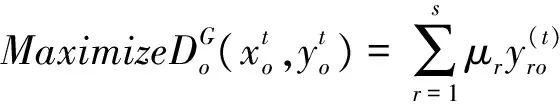
(14)
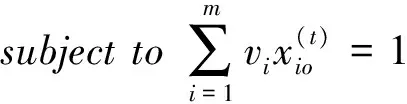
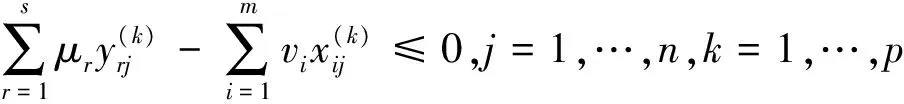
μr,vi≥0,r=1,…,s;i=1,…,m,
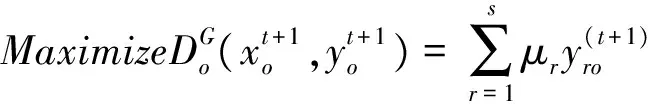
(15)

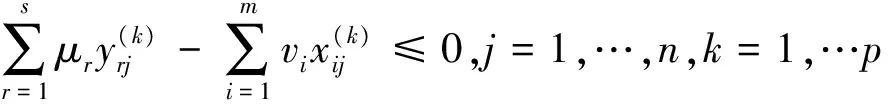
μr,vi≥0,r=1,…,s;i=1,…,m,
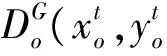
(16)
该指数也可以分解为如下两部分:
(17)
其中OECo与2.1节中的含义相同,而OGTCo度量的是乐观前沿面下全局技术变化与相邻时期技术变化之间的差异,可以视为一种新的技术进步度量方法。Pastor等[15]指出该指数满足循环性检验,有关循环性检验的讨论以及证明参见Pastor等[34]。
3.2 基于悲观前沿面下的全局DEA-Malmquist指数
悲观前沿面下的全局DEA-Malmquist指数也只需要测算t时期和 (t+1)时期相对全体时期的效率变化值,即求解如下两个模型:
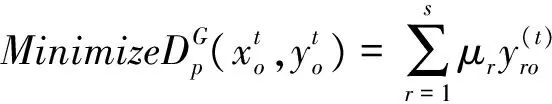
(18)
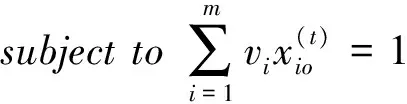
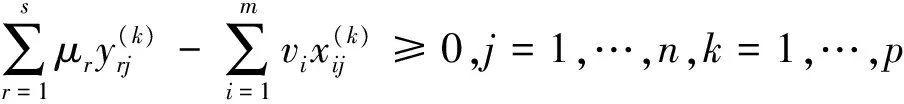
μr,vi≥0,r=1,…,s;i=1,…,m,
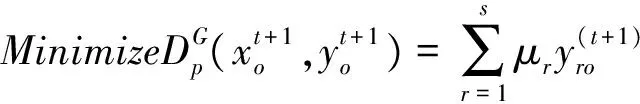
(19)

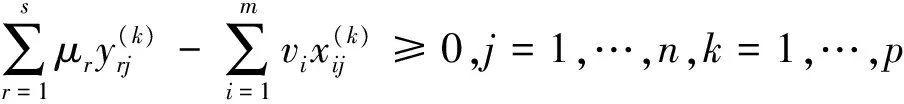
μr,vi≥0,r=1,…,s;i=1,…,m,
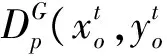
(20)
该指数也可以分解为两部分如下的两部分:
(21)
其中PECo与2.2节中的含义相同,而PGTCo度量的是在悲观前沿面下全局技术变化与相邻时期技术变化之间的差异。下面的定理1表明,GMPIo(Pessimistic)指数满足循环性检验。
定理1. 基于悲观前沿面下的全局DEA-Malmquist指数满足循环性检验。
证明:记GMPIo(Pessimistic)为PGMPIo。根据(20)式可知:
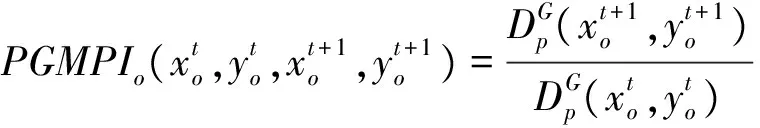
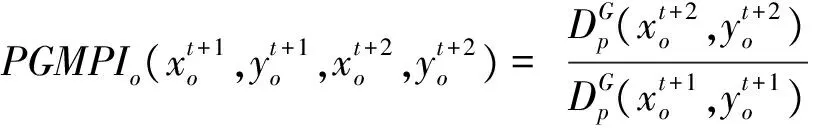
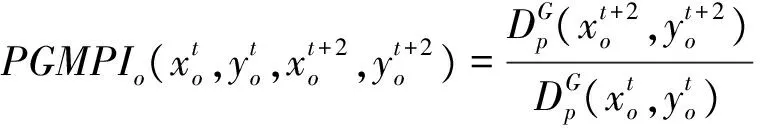
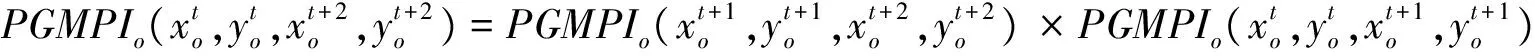
3.3 双前沿面下的全局DEA-Malmquist指数
为了避免前沿面选择的不同而导致的差异,本文亦采用几何平均数的方式将两指数进行综合。故双前沿面下的全局DEA-Malmquist指数可以表示为:
GMPIo(DFDEA) =[GMPIo(Optimistic)·GMPIo(Pessimistic)]1/2=[(OECo·OGTCo)(PECo·PGTCo)]1/2=[OECo·PECo]1/2[OGTCo·PGTCo]1/2=ECo·GTCo
(22)
上式中ECo与2.3节中双前沿面下的效率变化的含义一致;而GTCo测度的是全局技术变化。
定理2. 基于双前沿面下的全局DEA-Malmquist指数满足循环性检验。
证明:记GMPIo(Optimistic)为OGMPIo,GMPIo(DFDEA)为DFGMPIo。根据Pastor等[15]的研究可知,基于乐观前沿面的全局DEA-Malmquist指数满足循环性检验,即有:
又根据定理1可知,基于悲观前沿面的全局DEA-Malmquist指数均满足循环性检验,即有:
根据全局DEA-Malmquist指数的定义,即公式(22)可知:
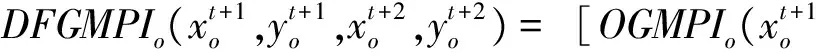
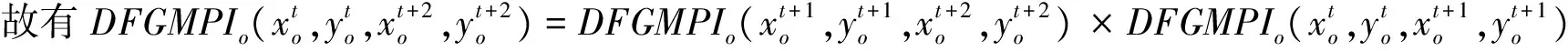
4 算例分析
4.1 变量及其数据说明
本文以工业部门为研究样本,分析福建省2001-2008年24个工业行业的生产率变动。按照工业划分标准并且结合《中国工业经济统计年鉴》中分地区的行业的情况并根据福建省自身工业行业的特点选择了24个二位码的工业行业进行分析。受统计数据的影响,该实证研究的对象为煤炭工业,石油工业,冶金工业,机械工业,食品工业,纺织工业,造纸工业以及化学工业。
在投入和产出变量的确定上,本文采用四个投入要素(全部从业人员平均人数、固定资产年均余额、流动资产年均余额)和单产出(总产值)。所涉及的变量如下:
产出数据。本文在借鉴陈勇等[24]的研究基础上,选用24个工业行业总产值作为衡量产出指标。基础数据来源于《中国工业经济统计年鉴》(2002-2009),并根据《福建省统计年鉴》(2002, 2005, 2007, 2010) 的“分行业工业品出厂价格指数”折算为2000年不变价。
资本投入数据。陈勇等[24]在研究资本投入数据时,采用固定资本年均余额 (反映固定资本投入) 和流动资本年均余额 (反映流动资本投入) 的平均值作为资本投入的基础数据。笔者认为,由于工业行业的共同特征为固定资本投入较高,各行业绝对值差异较大,而且对流动资本的需求也各不相同,因而本文直接将固定资产年均余额和流动资本的年均余额作为两个独立的资本投入变量,并按照各行业工业品出厂价格指数折算成2000年不变价。数据来源于《中国工业经济统计年鉴》(2002-2009)。
劳动投入数据。由于缺乏既能体现劳动者劳动时间又能体现劳动效率的统计指标,在借鉴前人研究的基础上,本文采用职工年平均人数(反映劳动力投入)来度量劳动投入。数据来源同上。
由于工业行业之间的异质性,本文在借鉴李廉水等[23]的处理方法的基础上,并结合从《中国工业经济统计年鉴》可以获取的地区工业行业部门数据的基础上,将福建省24个工业行业部门分为8大类,分别估算各类产业的生产率指数,从而获得更加全面更具有针对性的结果。具体的分类方法如下:
煤炭工业:煤炭开采和洗选业;
石油工业:石油加工、炼焦及核燃料加工业, 电力、热力的生产和供应业;
冶金工业:黑色金属矿采选业,黑色金属冶炼及压延加工业,有色金属冶炼及压延加工业,有色金属矿采选业;
食品工业:农副食品加工业,食品制造业,饮料制造业,烟草制品业;
纺织工业:纺织业;
造纸工业:造纸及纸制品业;
化学工业:化学原料及化学制品制造业,医药制造业,化学纤维制造业,非金属矿物制品业;
机械工业:金属制品业,通用设备制造业,专用设备制造业,交通运输设备制造业,电气机械及器材制造业,通信设备、计算机及其他电子设备制造业,仪器仪表及文化、办公用机械制造业。
4.2 主要结果及其分析
本文采用Matlab 7 (R2011a) 软件包,对福建省工业行业的全要素生产率进行估算,并将Malmquist指数分解为技术效率变化指数和技术进步指数,其中的这些指数所采用的符号沿用前面所给出的简写形式。
图1为福建省八大类工业行业2001-2008年间平均生产率指数及其分解。从图1中很直观的可以看出:在2001-2008年间,福建省八大类工业行业的平均生产率均呈现正增长的态势。其中,煤炭工业的平均生产率增长最快,其次是造纸工业,排在第三的是食品工业,而化学工业以微弱的劣势排在第四,第五位是冶金工业,机械工业位居第六,纺织工业排名第七,石油工业排在最后。从图1还可以很直观的看出技术效率(EC)与技术进步(GTC)对DFGMPI的贡献。总体上看,技术进步对福建省工业行业的平均生产率均起正向推动作用,且其大于技术效率所发挥的作用。从八大类工业行业来看,技术效率和技术进步对煤炭工业生产率的增长所起的作用相当,与之类似的还有石油工业、造纸工业和化学工业;对冶金工业和食品工业生产率增长所起的作用中的技术效率不如技术进步明显,与之相似的还有机械工业,只不过机械工业技术效率增长非常微弱;而纺织工业的生产率增长主要来源于技术进步,因为其技术效率为负增长。
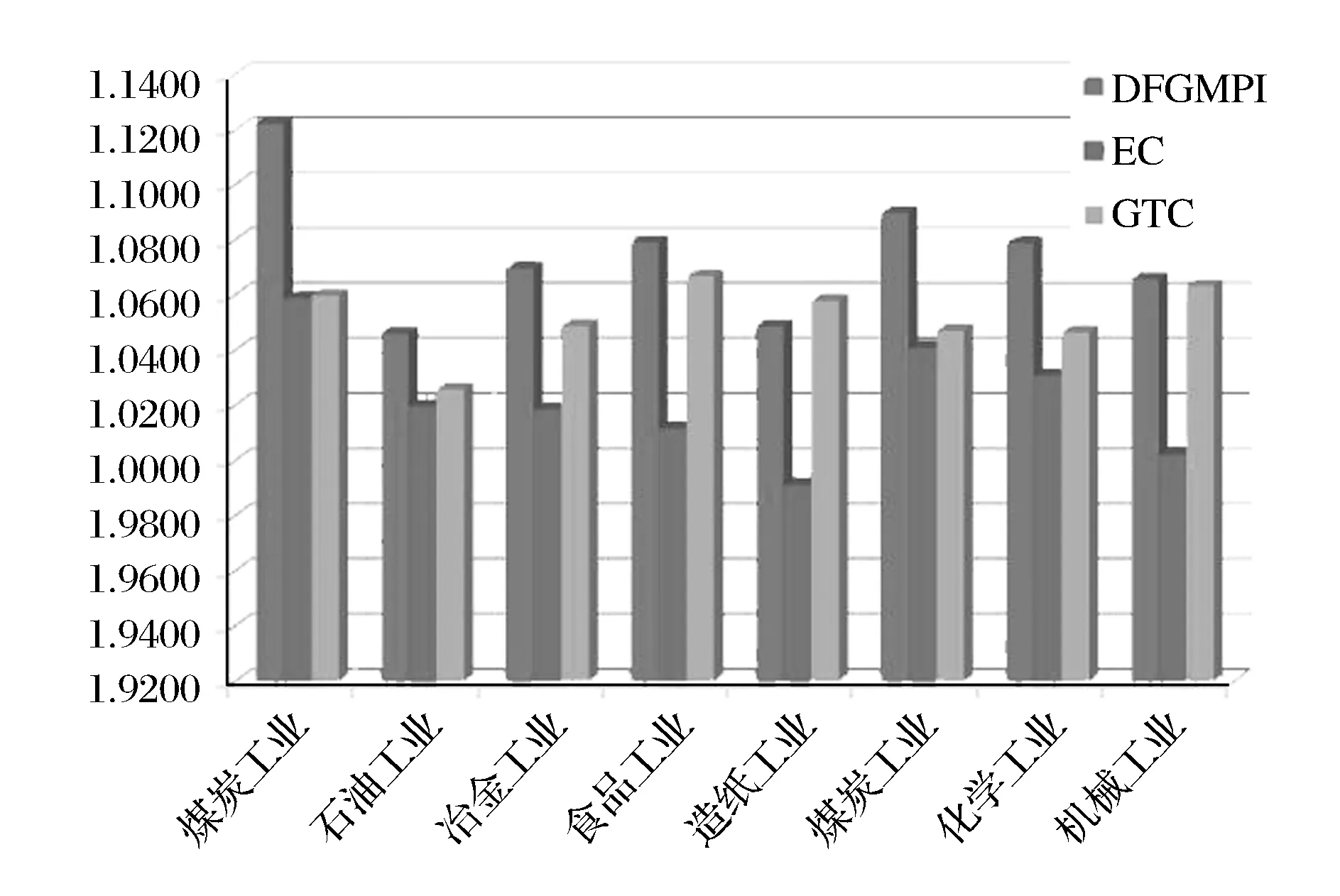
图1 福建省八大类工业行业2001-2008年间平均生产率指数及其分解
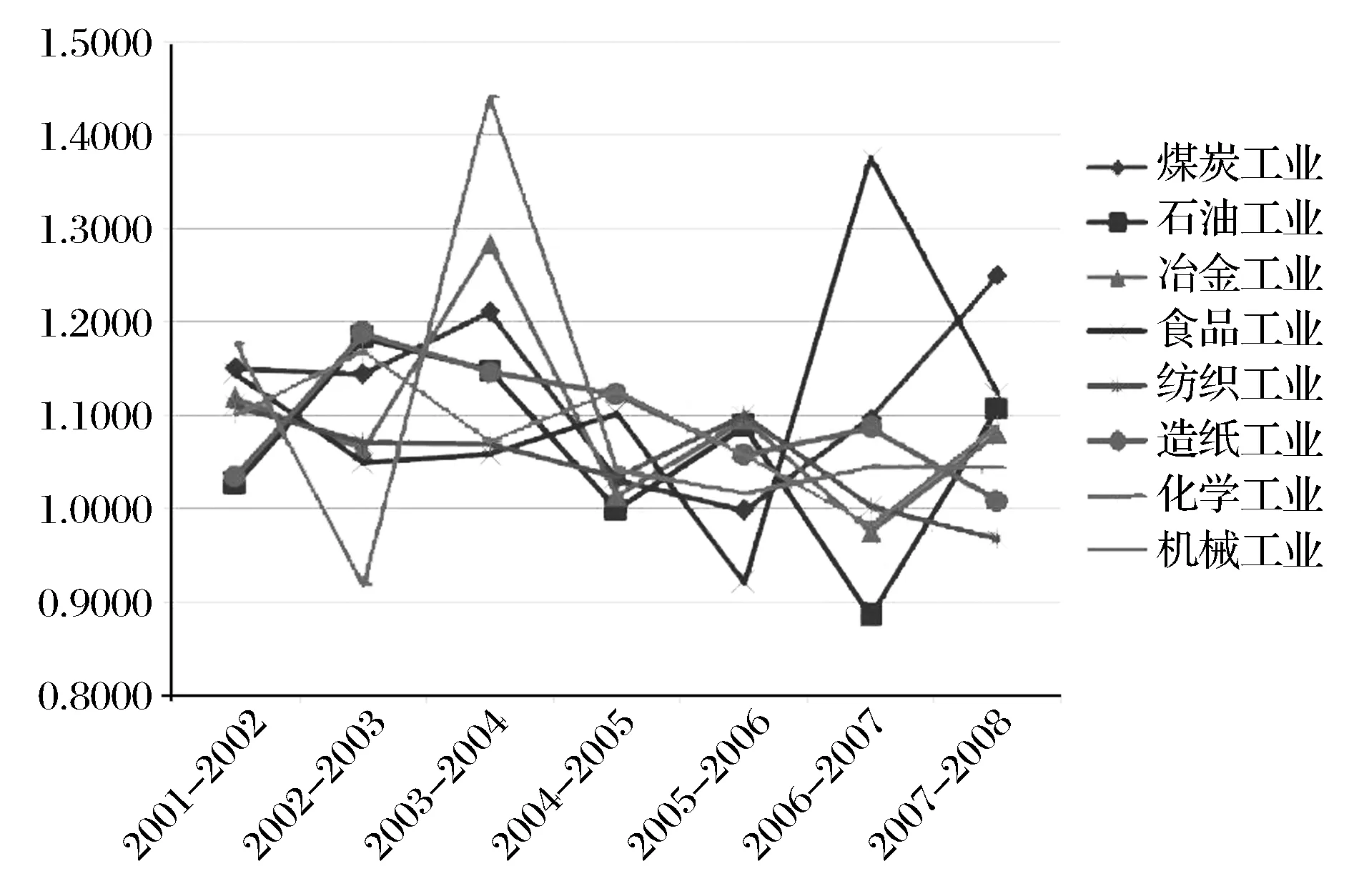
图2福建省八大类工业行业2001-2008年生产率指数变化情况
图2中的结果是福建省八大类工业行业2001-2008年在双前沿面下的全局Malmquist指数的变化情况。根据图2,可以得到如下结论:机械工业在2001-2005年之间生产率变化最大,其生产率在2003-2004年间增长率超过了40%,为八大类工业行业中增长最快的工业。食品工业在2005-2008年之间生产率变化最大,其在2006-2007年间生产率增长接近40%,在八大类工业行业八年的增长率中排名第二。造纸工业的生产率虽有波动,但其在2001-2008年间均呈现正增长的态势,与之类似的还有煤炭工业,只不过该工业2005-2006年间生产率接近于1。石油工业在2006-2007年间的增长率为八大类工业行业中最低的,呈现负的增长态势,其增长率为-11.58%。
表1给出了六种Malmquist指数,依次为:双前面下全局Malmquist指数(DFGMPI)、乐观前沿面下全局Malmquist指数(OGMPI)、悲观前沿面下全局Malmquist指数(PGMPI)、双前沿面下Mamquist指数(DFMPI)、乐观前沿面下Malmquist指数(OMPI)以及悲观前沿面下Malmquist指数(PMPI),分别由公式(22)、公式(16)、公式(20)、公式(13)、公式(5)以及公式(11)计算所得。表1中的结果是通过将2001-2002, 2002-2003, 2003-2004, 2004-2005, 2005-2006, 2006-2007, 2007-2008总共7个时期的生产率指数经过几何平均的方式集结所得(由于篇幅所限,本文未给出7个时期具体结果,有需要可以向作者索取),因此表1中的结果是2001-2008年间全体时期生产率的变动情况。从表1的各种生产率指数的对比中可以看出,不同前沿面下的结果之间存在着显著的差异。例如:2001-2008年福建省24个工业行业,乐观前沿面下全局Malmquist指数增长8.35%,而悲观前沿面下的增长6.05%。如果同时考虑两个前沿面的信息,即双前沿面下全局全要素生产率平均增长7.18%。对比表1中的OMPI与PMPI可以看出:福建省24个行业在OMPI度量下所得的全要素生产率均呈现为正增长的态势,而采用PMPI度量所得的全要素生产率有三个行业的生产率低于1,它们分别为石油加工、炼焦及核燃料加工业(-4.53%)、黑色金属冶炼及压延加工业(-7.9%)和交通运输设备制造业(-0.2%)。对比OGMPI与PGMPI可以发现:黑色金属冶炼及压延加工业在OGMPI度量下其生产率为正增长(1.59%),而采用PGMPI度量则呈现负增长(-11.75%),两种方法所得的结论相去甚远。从这些比较结果可以看出,由于前沿面选择的不同所得的结果存在一定的差异,然而这两种被参考的前沿面所代表的参考对象不同,因此只考虑任何一个前沿面而忽视另一个所得的结果都是有失偏颇的。对比两种双前沿面下的结果,即DFGMPI与DFMPI,我们可以发现虽然每个工业行业所得这两种生产率之间是存在差异的,但是这两种方法所得的结果在增长态势上保持一致,即除了石油加工、炼焦及核燃料加工业以及黑色金属冶炼及压延加工业之外的其余22个行业全要素生产率都呈现出正增长的态势。
5 结语
以t期所在的技术前沿面为参考的Malmquist指数往往与以 (t+1) 期所在的技术前沿面为参考所得Malmquist指数不一致,且Malmquist指数在一般情况下不满足指数检验中的循环性检验。为了实现该指数的循环性检验,Pastor等[15]提出了全局的Malmquist指数的测算方法。由于传统Malmquist 指数都是建立在乐观前沿面上,没有考虑悲观前沿面的影响。为了避免前沿面选择的不同而导致的差异,Färe等[35]提出了同时考虑两种前沿面下的Malmquist指数计算方法。本文对上述两个研究的结果进行了进一步的扩充,将全局效率分别引入乐观前沿面和悲观前沿面的Malmquist指数的计算中,得到双前沿面下全局Malmquist指数的计算方法,从而使得Malmquist指数满足循环性检验并且可以避免因基期选择不同而导致的差异,最后以福建省2001-2008年工业部分行业的生产率测算为例进行说明。采用双前沿面下全局Malmquist指数的结果表明,福建省八大类工业行业的平均生产率均呈现正增长的态势,其中技术进步的均起正向推动作用且其大于技术效率的所起的作用。另外,本文还将六种不同Malmquist指数进行对照分析,从算例分析的结果可知,由于前沿面选择的不同所得结果存在一定的差异,而两种基于双前沿面数据包络分析下的生产率指数较好的综合了两个前沿面的信息,从而所得的度量结果更具有可信性。
从本文的研究可以发现,双前沿面下全局Malmquist指数不仅继承了传统Malmquist指数的优点(陈勇等[24]),而且还具有以下三个优点:
(1) 可以避免前沿面选择的不同而导致的差异,能够较好的综合两个前沿面的信息,使得结果更加可信。
(2)因为采用全体时期的技术为参照,从而测得的各个时期的效率具有可比性,同时也避免了因为选择的基期的不同而导致的差异。
(3) 满足传统Malmquist指数一般不满足的指数检验——循环性检验。
[1] Malmquist S.Index numbers and indifference surfaces [J]. Trabajos de Estatistica, 1953, 4 (2): 209-242.
[2] Shephard R W. Cost and production functions [M]. Princeton: Princeton University Press, 1953.
[3] Caves D W, Christensen L R, Diewert W E. The economic theory of index numbers and the measurement of input, output, and productivity [J]. Econometrica, 1982 , 50 (6): 1393-1414.
[4] Färe R, Grosskopf S, Lindgren et al.Productivity change in Swedish pharmacies 1980-1989: A nonparametric Malmquist approach [J]. Journal of Productivity Analysis, 1992, 3 (3): 85-101.
[5] Farrell M J. The measurement of productivity efficiency [J]. Journal of the Royal Statistical Society Series A: General, 1957, 120 (3): 253-281.
[6] Färe R, Grosskopf S, Norris M,et al. Productivity growth, technical progress, and efficiency change in industrialized countries[J]. The American Economic Review, 1994, 84(1): 66-83.
[7] Ray S, Desli E. Productivity growth, technical progress and efficiency change in industrialized countries: comment[J]. The American Economic Review, 1997, 87 (5): 1033-1039.
[8] Färe R, Grosskopf S, Norris M. Productivity growth, technical progress, and efficiency change in industrialized countries: reply[J]. The American Economic Review, 1997, 87 (5): 1040-1043.
[9] Lovell C A K. The decomposition of Malmquist productivity indexes [J]. Journal of Productivity Analysis, 2003, 20 (3): 437-458.
[10] Grosskopf S. Some remarks on productivity and its decompositions[J]. Journal of Productivity Analysis, 2003, 20 (3): 459-474.
[11] 章祥荪, 贵斌威. 中国全要素生产率分析:Malmquist指数法述评与应用[J]. 数量经济技术经济研究, 2008, (6): 111-122.
[12] Chung Y H, Fare R, Grosskopf S. Productivity and undesirable outputs: a directional distance function approach[J]. Journal of Environmental Management, 1997, 51 (3): 229-240.
[13] Griefll-Tatjé E, Lovell C A K. A generalized Malmquist productivity index[J]. TOP, 1999, 7 (1): 81-101.
[14] Chen Yao. A non-radial Malmquist productivity index with an illustrative application to Chinese major industries [J]. International Journal of Production Economics, 2003, 83 (1): 27-35.
[15] Pastor J T, Lovell C A K. A global Malmquist productivity index [J]. Economics Letters, 2005, 88 (2): 266-271.
[16] Lo S F, Lu Weimin. An integrated performance evaluation of financial holding companies in Taiwan [J]. European Journal of Operational Research, 2009, 198 (1): 341-350.
[17] Kao C. Malmquist productivity index based on common-weights DEA: The case of Taiwan forests after reorganization [J]. Omega, 2010, 38 (6): 484-491.
[18] Oh D. A global Malmquist-Luenberger productivity index [J]. Journal of Productivity Analysis, 2010, 34(3): 183-197.
[19] Pastor J, Asmild M, Lovell C A K. The biennial Malmquist productivity change index[J]. Socio-Economic Planning Sciences, 2011, 45 (1): 10-15.
[20] Tohidi G, Razavyan S. A circular global profit Malmquist productivity index in data envelopment analysis [J]. Applied Mathematical Modelling, 2013, 37(1): 216-227.
[21] Kao C, Hwang S N. Multi-period efficiency and Malmquist productivity index in two-stage production systems [J]. European Journal of Operational Research, 2014, 232(3): 512-521.
[22] 李小平, 朱钟棣. 中国工业行业的全要素生产率测算——基于分行业面板数据的研究[J]. 管理世界, 2005, (4): 56-64.
[23] 李廉水, 周勇. 技术进步能提高能源效率吗?——基于中国工业部门的实证检验[J]. 管理世界, 2006, 10: 82-89.
[24] 陈勇, 李小平. 中国工业行业的技术进步与工业经济转型——对工业行业技术进步的DEA法衡量及转型特征分析[J]. 管理世界, 2007, (6): 56-63.
[25] Odeck J. Statistical precision of DEA and Malmquist indices: A bootstrap application to Norwegian grain producers [J]. Omega, 2009, 37 (5): 1007~1017.
[26] 解百臣, 杜纲. 效用型Malmquist 指数方法及火电类上市公司实证分析[J]. 中国管理科学, 2010,18(1): 46-51.
[27] Gitto S, Mancuso P. Bootstrapping the Malmquist indexes for Italian airports [J]. International Journal of Production Economics, 2012, 135(1): 403-411.
[28] Egilmez G, McAvoy D. Benchmarking road safety of US states: A DEA-based Malmquist productivity index approach [J]. Accident Analysis & Prevention, 2013, 53(1): 55-64.
[29] Wang Yingming, Chin K S, Yang J B. Measuring the performances of decision making units using geometric average efficiency [J]. Journal of the Operational Research Society, 2007, 58 (7): 929-937.
[30] Wang Yingming, Chin K S. A new approach for the selection of advanced manufacturing technologies: DEA with double frontiers [J]. International Journal of Production Research, 2009, 47 (23): 6663-6679.
[31] Wang Yingming, Lan Yixin. Measuring Malmquist productivity index: A new approach based on double frontiers data envelopment analysis [J]. Mathematical and Computer Modelling, 2011, 54 (11-12): 2760-2771.
[32] Førsund F R. On the circularity of the Malmquist productivity index [Z]. ICER working papers, 2002.
[33] 康梅, 冯英浚. 基于非参数-参数法的一致Malmquist生产率指数[J]. 系统工程理论与实践, 2006, 6: 30-34.
[34] Pastor J T, Lovell C A K. Circularity of the Malmquist productivity index [J]. Economic Theory, 2007, 33 (3): 591-599.
[35] Färe R, Grosskopf S. Intertemporal production frontiers: with dynamic DEA [M]. Kluwer Academic Publisher, Boston, 1996.
Measuring Malmquist Productivity Index: A Circular Global Approach Based on Double Frontiers Data Envelopment Analysis
WANG Ying-ming, LAN Yi-xin
(Decision Science Institute, Fuzhou University, Fuzhou 350116, China)
Measures of productivity growth constitute core indicators for the analysis of economic growth. The data envelopment analysis (DEA)-based Malmquist quantity index has enjoyed widespread use in a production context. By using all the periods to construct a global benchmarking technology frontier, the double frontiers data envelopment analysis (DFDEA)-based Malmquist productivity index is extended to acquire a DFDEA-based global Malmquist productivity index, which can avoid the differences in evaluation results resulted from the arbitrary choice of frontiers and base periods. This global index integrates the information on both the optimistic frontier and the pessimistic frontier and can meet the requirement of circular test. This global Malmquist productivity index is applied to investigate the behaviors of the industrial sectors of Fujian province during the years 2001 to 2008. The application results have clearly shown that our approach is more comprehensive and more realistic than the traditional DEA-based MPI in measuring productivity index.
data envelopment analysis; Malmquist productivity index; double frontiers data envelopment analysis; global malmquist productivity index; circular test
2013-12-09;
2014-07-29
国家自然科学基金资助项目(71371053);高等学校博士学科点专项科研基金资助项目(20123514110012); 教育部人文社会科学研究青年基金资助项目(14YJC630056);福建省自然科学基金资助项目(2014J01264)
王应明 (1964-),男(汉族),福州大学经济与管理学院,教授,博士生导师,研究方向:决策理论与方法、数据包络分析、规则库推理、质量功能展开.
1003-207(2015)11-0046-10
10.16381/j.cnki.issn1003-207x.2015.11.006
C934
A

