大型复合材料构件固化变形分析方法研究进展*

西北工业大学航空学院 郑锡涛 刘振东 梁 晶

整体成型的大型复合材料构件能够减轻结构重量、减少零件数量、降低生产成本与装配成本。然而，由于材料本身的各向异性、基体的固化收缩效应、构件与模具之间的相互作用等因素，结构内部将不可避免地产生残余应力，进而引起复合材料结构件在脱模后产生回弹变形以及翘曲变形。这种固化变形会产生一定的尺寸误差，从而使复合材料构件无法满足现代飞机无应力装配的要求，这种现象在大型飞机复合材料构件上尤为明显。为预测并控制这种变形，国内外学者对复合材料的固化变形进行了大量研究。本文将对影响固化过程的各个因素进行简要分析，并给出有限元分析方法。

复合材料构件固化过程中的温度场分析

先进航空复合材料构件采用热压罐工艺成型时，在升温过程中的热源有2个：外热源（热压罐的加热过程）；内热源（树脂基复合材料固化放热过程）。

1 外部热源对复合材料固化过程中温度场的影响

外热源对固化过程的影响主要表现在热压罐环境温度变化导致模具温度发生改变，进而影响复合材料构件的温度场。目前，外热源对复合材料温度场的影响，主要集中在2方面：（1）热压罐内气体流动传热过程导致的热压罐内部温度场分布不均匀；（2）模具设计原因导致的模具型面温度场分布不均匀。

针对热压罐内部温度场分布情况，张铖等[1]利用计算流体力学中的三维非定常N-S方程，以及湍流模型，模拟了热压罐强迫对流换热条件下的温度场分布情况。贾成贵等[2]经过试验，测得有效工作容积为φ2.6m×8.0m的热压罐，实际达到的温度均匀度为±2.5℃，热压罐空载温度场均匀度较好。针对模具因素导致的型面温度场不均匀，张铖等[1]研究了热压罐内采用框架式模具进行固化成型时，框架式模具型面上的温度场分布情况。梁宪珠等指出框架式模具升降温快，有利于模具各点温度均匀[3]。

由于框架式模具各点温度分布较为均匀，国内外学者在分析复合材料固化过程中，往往忽略外部温度场不均匀性，采用固化温度作为温度边界条件施加在复合材料构件上，以此模拟外部热源对复合材料温度场的影响。

2 内部热源对复合材料固化过程中温度场的影响

内热源是由于复合材料在固化过程中，树脂材料发生化学反应释放能量引起的。一般热固性树脂在固化反应中，单位时间内单位体积中的内热源放热量Φ与固化反应的进程相关，可以用式（1）表示[4]：

式中，ρr为树脂的密度；Vr为树脂的体积分数；Hr为单位体积树脂的总反应热；dα/dt为树脂的固化反应速率，其中α为树脂的固化度，固化度取值范围为α∈[0，1]，0代表固化反应尚未开始，1代表固化反应已经结束。

3 复合材料构件固化过程中的温度场分析

大多数的研究者采用傅里叶热传导控制方程描述复合材料固化过程中的热传导，复合材料构件中的热平衡方程可以采用式（2）表达。

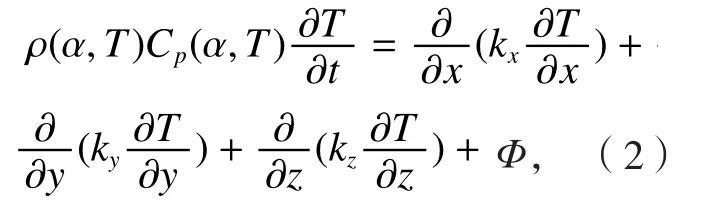
式中，ρ（α，T）为复合材料密度；Cp（α，T）为复合材料比热容；T为绝对温度；kx、ky、kz分别为复合材料沿x、y、z方向的导热系数。

固化动力学模型

固化反应动力模型通过数学形式来描述在某时刻或温度下，树脂已转化的物质的量和转化速率之间的关系。目前，国内外学者对固化过程的描述主要分为唯象模型和机理模型[5]。从工程实践角度出发，唯象模型由于其简易性而广泛应用于有限元模拟计算中。

固化动力学模型多使用DSC（差示扫描量热）方法获得。目前，大多数固化动力学模型通过模型拟合法，建立在一些经验模型的基础上，一般用下面的数学模型表示：

式中，k(T)为反应速率函数，是温度T的函数，f(α)为固化度α的函数。

通常根据f(α)的不同可将固化动力学模型分为以下2类。

（1）n级反应动力学模型。n级反应动力学模型的特点是固化反应一开始便达到最大固化速率。n级反应动力学模型的具体形式为：

式中A为频率因子，ΔEa为活化能，R为普适气体常数。

（2）自催化模型。对于自催化模型，由于存在诱导期，固化速率极值出现在20%～40%附近。自催化模型的具体形式为：

式中，，k1和 k2为反应速率常数，Ai为是频率因子，m1(和ky∂nT1为)+反应∂ 级(kz数∂T，Δ)+EΦai为自催化模型的∂y活化能∂z。 ∂z

材料性能随固化反应的变化

随着固化反应的进行，复合材料的力学性能也会发生变化。目前模拟材料性能随化学反应变化的方式主要有两种：（1）由试验测定在不同的固化阶段下材料的力学性能，并进行拟合；（2）认为纤维性能不变，树脂性能随化学反应变化，然后从细观力学出发拟合复合材料性能。

White等[6]针对AS4/3501-6在不同固化度阶段下的性能进行了试验测定，认为复合材料的轴向模量E11可以采用线性公式拟合，横向模量E22可以以某一固化度为分界线，采用分段函数的形式表达。

Bogetti等[7]列出了与固化进程相关的树脂弹性模量表达式：

式中，Em为树脂的弹性模量，为树脂未固化时的弹性模量，为树脂固化完全时的弹性模量，αgel为树脂的凝胶点。

随后根据纤维与树脂的性能，采用细观模型对复合材料的力学性能进行拟合。

化学收缩对复合材料固化变形的影响

Yoon等[8]研究发现化学收缩对复合材料固化变形来说是至关重要的。针对化学收缩的模拟，文献中提供了2种方式：（1）将树脂基体化学收缩产生的应变等效地叠加在树脂基体的热膨胀中，通过等效热膨胀系数实现上述目标；（2）将化学收缩单独计算，在每一个分析步中，作为初始应变添加在模型上。

第一种方法采用的等效热膨胀系数难以完全模拟化学收缩，甚至在某一分析步中，在温度不变的情况下，该方法无法模拟可能发生的化学收缩。第二种方式需要将增量步调整的很小，才能较精确模拟化学收缩。本文重点介绍第二种方式。

树脂的化学收缩应变可以通过树脂固化度α计算[9]：

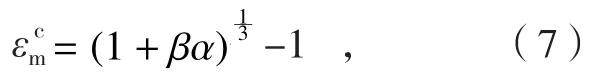
式中，β是由试验确定的树脂总体积的收缩，一般取值为2%～5%。认为纤维在固化过程中不发生化学收缩，复合材料的化学收缩可以根据细观力学模型确定，其中沿着纤维方向和垂直纤维方向的总应变量分别为：

式中，Vf为纤维体积分数；μm和μc分别为树脂和复合材料的泊松比；Em和Ef分别为树脂和纤维的弹性模量。

材料本构方程对复合材料固化变形的影响

分析复合材料固化过程，通常采用的材料本构关系有线弹性模型与粘弹性模型。Prasatya等[10]指出粘弹性效应对复合材料的残余应力来说是不可忽视的。郭兆璞等[11]采用粘弹性模型，计算得到1周后的残余应力的平均值比线弹性模型所得应力降低52%。线弹性模型与粘弹性模型不仅计算所得残余应力与固化变形量不同，甚至会得出相反的结论，例如采用线弹性模型，可以得到层合板的残余应力与降温过程无关，仅与Tg与TR的差值有关[12]；而采用粘弹性模型，则可以得到采用不等速降温，对降低层合板固化残余应力有利[11]，因此，在进行复合材料固化变形分析时，应当进行粘弹性分析。

温度对聚合物材料的力学性能有很大的影响，升高温度与延长时间对分子运动和聚合物的粘弹行为能产生等效的效果。这一效应称为聚合物材料的时间-温度等效原理[4]。

Kim等[13]通过试验测定了温度转换因子aT，利用温度转换因子可以将从温度T1到温度T2对粘弹性材料造成的影响转换到时间刻度上，降低了粘弹性分析难度。转换关系为：

式中，ξ为折算时间。

目前广泛采用的复合材料粘弹性模型是广义的Maxwell模型，该模型由（n-1）个Maxwell单元和一个弹簧组成。Kim等[13]对AS4/3501-6的粘弹性力学性质进行了研究，给出了由9个Maxwell单元以及1个弹簧单元组成的广义Maxwell模型。基于广义的Maxwell模型，正交各向异性的复合材料的本构关系为：

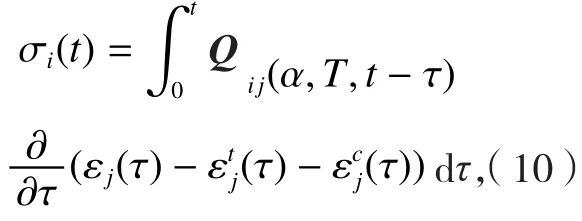
式中，σi为应力分量，Q ij为刚度矩阵，T为温度，εj为总应变量，为热应变分量，为化学应变分量。

当材料在达到某一固化度α0时呈现简单的热-流变性，式（10）可以改写成式（11）：

为完全松弛刚度矩阵，为初始刚度矩阵，Wm为第m支Maxwell单元的权重系数，τm为第m支Maxwell单元的离散应力松弛时间。

模具约束作用对复合材料构件固化变形的影响

模具对复合材料构件固化变形的影响主要集中在2个方面：（1）模具原因引起的层合板内温度分布梯度；（2）模具和复合材料热膨胀系数差异而引起的相互作用。Satish[14]在研究模具约束作用时，采用了剪切层来代替模具对复合材料的作用，通过改变剪切层的厚度以及热膨胀系数使模拟结果接近试验值，但是该方法所得的剪切层参数仅对给定的固化压力与结构尺寸下有效。岳广全[15]对剪切层进行进一步的研究，建立了剪切层厚度与热膨胀系数与复合材料构件尺寸及固化压力之间的数学模型，扩展了剪切层参数的应用范围，但是依旧需要通过试验获得剪切层参数。根据以往的研究，模具约束作用导致的固化变形仅占10%左右[16]，因此多数学者会采用更加简单的边界条件约束来代替剪切层，模拟模具对复合材料构件固化过程的影响。

固化压力对复合材料构件固化变形的影响

固化压力对复合材料固化变形的影响主要体现在以下2个方面：（1）固化压力通过改变热压罐中的高温气流流动特性，进而影响复合材料构件的温度场；（2）固化压力通过改变树脂含量以及树脂分布来影响复合材料构件固化变形。

本节讨论改变树脂含量对复合材料构件固化变形量的影响。一方面，Yi等[17]研究得到，树脂含量会影响复合材料固化过程的温度场与固化度场分布，同时也会影响复合材料的化学收缩量，进而影响复合材料构件的固化变形。另一方面，压力分布不均匀导致压实不均匀，使各部分树脂含量不同，甚至造成贫脂区和富脂区，这种不均匀性也会影响构件的固化变形。杨进军[18]针对纤维树脂分布引起的固化变形进行了研究。目前多数学者为易于工程应用，往往忽略树脂不均衡带来的影响。

复合材料构件的固化变形分析实例

本文基于通用有限元分析软件ABAQUS 进行二次开发，得到了一套模拟复合材料固化变形的有限元程序。该程序忽略外部温度场不均匀性，并采用傅里叶热传导控制方程；固化动力学模型采用胡照会[9]给出的模型；材料性能随固化反应变化的趋势采用S.R.White[6]所给形式；化学收缩采用式（8）所给形式；利用边界条件约束代替模具对构件的影响，并忽略了固化压力引起的树脂不均匀。

本文利用上述程序模拟了L型筋条、 L 型加筋壁板的固化变形情况，如图1所示。筋条长度为 300mm，凸缘宽度为 20mm，倒角半径为 3mm，铺层厚度为 1mm。筋条 的 铺 层 形 式 为 [90/-45/0/45/-45/0/45/90]T。多筋壁板的平板尺寸为300mm×200mm× 1mm ，蒙皮铺层形式为[90/-45/0/-45/45/0/-45/90]T，筋条铺层形式为 [90/-45/0/ -45/45/0/-45/90]T。表1列出了试件的实际变形量与本文模拟变形量的对比。

结束语

复合材料构件在航空航天领域取得了广泛的应用。相对于小型构件，大型复合材料构件的固化变形量相对较大，会影响复合材料构件的装配，使其难以满足无应力装配的要求，强行装配会产生较大的装配应力，影响复合材料构件的性能与使用寿命。

图1 L型筋条与多筋壁板的固化变形形式

针对复合材料固化变形，国内外学者已经做了大量的研究工作，固化变形的基础理论研究已经较为成熟，但在工程实践应用中，复合材料构件的固化变形量计算方式尚有待提高。复杂模型分析所得的变形量精度较高，但是计算量巨大，所需参数需要大量试验获得，难以大规模应用，并且通用性较差；简单模型计算速度较快，但误差较大，难以对工程应用产生指导作用。因此，对影响固化变形量的各个因素进行合理的简化，建立一种精度较高，通用性较强，能够广泛应用于工程实践的大型复合材料构件固化变形分析方法是目前亟待解决的问题。综述. 玻璃钢/复合材料, 2009(3):81-85.

表1 复合材料试件的变形量

[1] 张铖, 梁宪珠, 王永贵,等. 热压罐工艺环境对于先进复合材料框架式成型模具温度场的影响. 材料科学与工程学报, 2011(4):547-553.

[2] 贾成贵, 朱振生, 王维纲. 大型热压罐装置. 航空工程与维修, 1997 (3):38-39.

[3] 王永贵, 梁宪珠, 曹正华,等. 热压罐工艺成型先进复合材料构件的温度场研究

[4] 王晓霞. 热固性树脂基复合材料的固化变形数值模拟[D].济南：山东大学, 2012.

[5] 蔡宏洋. 低粘度中温固化环氧树脂体系研究[D]. 北京：北京化工大学, 2008.

[6] White S R, Hahn H T. Process modeling of composite materials: residual stress development during cure. Part II. Experimental Validation7. Journal of Composite Materials,1992, 26:2423-2453.

[7] Bogetti T A, Gillespie J W. Processinduced stress and deformation in thick-section thermoset composite laminates. Journal of Composite Materials, 1992, 26(5):626-660.

[8] Yoon K J, Kim J S. Effect of thermal deformation and chemical shrinkage on the process induced distortion of carbon/epoxy curved laminates. Journal of Composite Materials, 2001,35(3):253-263.

[9] 胡照会, 王荣国, 赫晓东,等. 复合材料层板固化全过程残余应变/应力的数值模拟. 航空材料学报, 2008, 28(2):55-59.

[10] Prasatya P, Mckenna G B, Simon S L. A viscoelastic model for predicting isotropic residual stresses in thermosetting materials:effects of processing parameters. Journal of Composite Materials, 2001, 35(10):826-848.

[11] 郭兆璞, 陈浩然, 段滋华. 复合材料层合板粘弹性固化残余应力分析. 计算力学学报, 1996 (4):401-407.

[12] 郭兆璞, 陈浩然. 复合材料层合板在加工固化后期降温速率对残余热应力. 计算力学学报, 1995(4):387-393.

[13] Kim Y K, W h ite S R. Stress relaxation behavior of 3501‐6 epoxy resin during cure . Polymer Engineering & Science, 1996,36(23):2852-2862.

[14] Bapanapalli S K, Smith L V. A linear finite element model to predict processinginduced distortion in FRP laminates . Composites Part A: Applied Science & Manufacturing, 2005,36(12):1666-1674.

[15] 岳广全. 整体化复合材料壁板结构固化变形模拟及控制方法研究[D]. 哈尔滨：哈尔滨工业大学, 2010.

[16] 庞杰. 复合材料结构固化变形分析及其控制[D]. 南京：南京航空航天大学, 2010.

[17] Yi S, Hilton H H. Effects of thermomechanical properties of composites on viscosity,temperature and degree of cu re in thick thermosetting composite laminates during curing process. Journal of Composite Materials, 1998,32(7):600-622.

[18] 杨进军. 纤维分布对复合材料固化变形的影响. 纤维复合材料, 2010, 27(1):13-17.